双隐含层BP神经网络模型在老哈河水质预测中的应用

2018-05-22查木哈卢志宏翟继武张福顺

水资源与水工程学报 2018年2期

查木哈, 卢志宏，翟继武，张福顺

(1.赤峰市环境监测中心站，内蒙古赤峰 024000; 2.铜仁学院，贵州铜仁 554300；3.中国农业科学院草原研究所，内蒙古呼和浩特 010010)

1 研究背景

水资源是经济社会可持续发展和生态文明建设不可替代的基础性自然资源和战略资源[1]。随着社会经济的快速增长和人民生活水平的不断提高，人们对水资源的需求不断增大，对水环境系统造成了持续的高强度的破坏。生产废水、生活污水的排放以及降雨径流携带地表污染物汇入河流等因素，导致河流水质不断恶化[2]。水环境污染是多种因素影响的结果，具有非线性、不确定性和模糊性。水质预测，通常是利用历史数据，通过不同的预测方法推求环境变量与待预测水质指标之间的非线性关系或待预测水质指标本身随时间的变化规律[3]。

人工神经网络是一种非线性的、能够模拟人类大脑思维活动的数学模型[4-5]，BP神经网络是目前发展最为成熟、应用最为广泛的一种网络模型，其具有完整的理论推导过程。国内外学者把人工神经网络引入到水质动态预测中，BP神经网络模型在多个区域河流水质预测中得到具体应用，郑鹏[6]运用改进的BP神经网络模型预测辽宁中部河流水质，郭亮等[7]应用人工神经网络技术对松花江四方台高锰酸盐指数进行预测，高雅玉等[8]把改进的BP神经网络应用到双塔水库水质的预测中，李占东等[9]应用BP人工神经网络模型评价珠江水质，陈文花[10]应用BP神经网络模型对水质变化趋势做出预测。目前的预测和评价模型多集中在单隐含层及优化算法方面，多层隐含层BP神经网络模型在水质预测中的应用较少，而影响河流水质的因素很多，是一个复杂的系统，一般认为单隐含层模型能够处理简单的问题，多个隐含层的模型适合于处理比较复杂的问题。因此本文尝试应用双层隐含层的BP神经网络模型对老哈河水质进行预测分析，采用赤峰段甸子点位2010-2014年化学需氧量、五日生化需氧量、高锰酸盐指数、总磷浓度这4项污染指标为样本训练数据，建立双隐含层BP 人工神经网络模型，预测2015年的水质变化情况，验证BP神经网络模型对老哈河水质预测的准确性，探讨 BP 神经网络模型运用于水质预测的可行性与适用性，为水环境管理和水污染控制提供科学依据。

2 材料与方法

2.1 研究区概况

作为西辽河的源头，老哈河流域地处河北、辽宁两省与内蒙古自治区交界，是我国重要的重工业、能源和商品粮生产基地。该流域形状呈不对称扇形，介于41°N ～ 43°N、117° E ～ 120° E 之间，流域内地形复杂，地势西高东低起伏较大，海拔 427～2 017 m。老哈河发源于河北省平泉县西北山区柳溪满族乡，从宁城县甸子乡入内蒙古赤峰市境内，流经赤峰市东南部(喀喇沁、元宝山、松山区、敖汉)，全长约426 km，流域面积33 076 km2，河道总落差1 215 m，主要支流有黑里河，坤头河，锡伯河，英金河。老哈河流域属中温带半干旱大陆性季风气候，多年平均气温为7℃，平均降水量为430.89 mm，流域内降雨量年际和年内分配不均衡，丰枯变化大，老哈河天然径流主要来源于大气降水，属于降水补给型。

2.2 研究方法

选取的水质项目的确定，是根据《地表水环境质量标准》(GB3838-2002)中规定的基本项目，并结合老哈河各断面水质污染状况，选取化学需氧量(CODCr)、五日生化需氧量(BOD5)、高锰酸盐指数(CODMn)、总磷(TP)等4项指标。按照地表水监测采样原则，进行水样采集，并按照《水和废水监测分析方法》(第4版)相关规定，采用国家标准方法进行测定。本文采用 2011-2014年每月老哈河赤峰段甸子点位水质监测数据预测2015年水质。

2.3 神经网络

2.3.1 BP网络结构 BP网络是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。网络包括输入层、输出层和隐含层，其中隐含层可以有多层。双隐含层BP网络的结构如图1所示，同层节点(单元)中没有任何耦合。从输入层输入信号节点，传过各隐含层节点，传到输出层，每一层节点的输出结果只影响下一层节点的输出结果，相邻层每个节点通过适当的连接权值和阈值前向连接。BP网络是非线性映射模型，能够学习和模拟任意复杂的非线性函数。

其中，x1，x2，…，xn为网络的输入向量，y1为输出向量，连接层与层之间的传递函数是连续可微的非线性函数，通常采用S形的对数或正切函数，如logsig函数和tansig函数；层与层之间的神经元通过权值wni、pij、wnj和阈值αi、qj、βk连接。

图1 双隐含层BP神经网络模型示意图

2.3.2 BP网络的训练在梯度下降法基础上建立的BP网络的训练学习过程，由误差信号正向和误差信号反向传播组成。误差信号正向传播的时候，每一层神经元的结果仅影响下一层神经网络，训练样本输入矩阵从输入层经过隐含层向前传播到输出层，并得出输出结果。假如输出结果未达到期望值，即输出值和期望值误差未达到预期精度，则网络转入反向传播过程，会将误差信号沿原本的连接通路撤回，并通过修改各层神经元的权值和阈值，逐次地向输入层传播进行计算，再经正向传播过程，通过两个过程的反复运行，直至达到预期精度值，网络训练结束。

2.3.3 BP网络的测试经过训练的BP网络结构构成后，各层之间的连接权值矩阵和各层阈值矢量均已确定，此网络就是实际应用运行的模型。此神经网络模型能否用于实践，是否达到预期目的，还需要对已确定的神经网络模型用已知的样本进行测试验证。假如测试精度达到预期要求，则证明该模型可以用于预测，否则还需要重新建立新的模型。网络模型测试过程就是用测试样本代入训练样本作为网络输入，计算网络输出结果，探讨其输出与测试样本目标的误差。经过训练的网络，再经过测试证实可行，即测试样本相对误差满足预期要求，就可用于预测。

2.4 模型构建

在网络学习过程中，为了消除输入样本间的量纲差异，以便更好地进行学习，需要对样本进行归一化处理：

(1)

(2)

(3)

(i=1, 2,……,n,n=12)

3 结果与讨论

3.1 缺失值

当缺失值存在时，往往会影响变化规律的模拟，在数值分析中，运用拉格朗日插值法补充缺失值。拉格朗日插值法是一种多项式插值方法，可以提供一个正好穿过二维平面上若干已知点的多项式函数。拉格朗日插值法的公式结构紧凑，在理论分析中应用方便[13]。

本文中因河流冬季冰冻，造成了5个月份数据的缺失，因此采用拉格朗日插值法进行插值，五日生化需氧量、化学需氧量、高锰酸盐指数、总磷插值情况如图2。2010年12月、2013年1-2月3个月的高锰酸盐、化学需氧量插值比较平滑，五日生化需氧量插值连续下降，总磷连续上升；2012年1、2月份，化学需氧量连续上升，五日生化需氧量、高锰酸盐和总磷连续下降。插值后的数据能够满足数值分析的要求。

图2 拉格朗日插值图

3.2 五日生化需氧量预测模型

经过试凑法确定五日生化需氧量最优模型的第一隐含层节点数为4，第二隐含层节点数为12，预测模型结构为 3-4-12-1。从图3可以看出，五日生化需氧量预测值与实测值的决定系数R2为0.751 6(P=0.0003)，4、7、11月份的误差较大，其余9个月的误差较小。

3.3 化学需氧量预测模型

经过试凑法确定化学需氧量最优模型的第一隐含层节点数为12，第二隐含层节点数为10，模型结构为 3-12-10-1。从图4可以看出，化学需氧量预测值与实测值的决定系数R2为0.887 5(P<0.0001)，4、12月份的误差较大，其余10个月的误差较小。

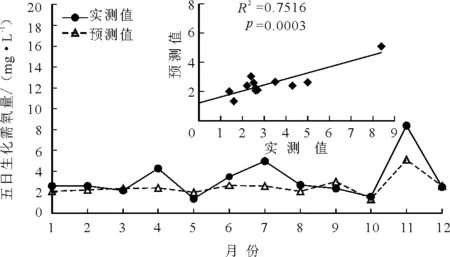
图3 五日生化需氧量浓度预测值与实测值对比

图4 化学需氧量浓度预测值与实测值对比

3.4 高锰酸盐指数预测模型

经过试凑法确定高锰酸盐最优模型的第一隐含层节点数为6，第二隐含层节点数为3，模型结构为 3-6-3-1。从图5可以看出，高锰酸盐指数预测值与实测值的决定系数R2为0.854 7(P<0.000 1)，9、10、11月份的误差较大，其余9个月的误差较小。

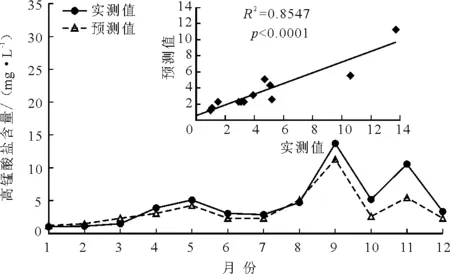
图5 高锰酸盐指数浓度预测值与实测值对比

3.5 总磷浓度预测模型

经过试凑法确定总磷最优模型的第一、第二隐含层节点数均为12，模型结构为 3-12-12-1。从图6可以看出，总磷浓度预测值与实测值的决定系数R2为0.889 2(P<0.000 1)，7、11、12月份误差较大，其余9个月的误差较小。

图6 总磷浓度预测值与实测值对比

3.6 预测精度分析

由表1可知，4个预测模型的回归系数从大到小依次为TP>CODCr>CODMn>BOD5(0.889 2>0.887 5>0.854 7>0.751 6)，平均相对误差依次为TP

表1 预测值与实测值误差分析

人工神经网络是一种非线性数学模型，能够模拟任意复杂程度的非线性过程，最大的优点是能够反复训练、测试网络结构，最终以任意精度逼近任意复杂的非线性函数，BP神经网络是应用范围最广泛的一种人工神经网络[5,14-15]。分析监测数据过程中发现，由于水质的变化一般都是渐变的过程，可通过历史监测数据的变化趋势来预测将来的水质指标，可达到较好的效果。本文以若干连续实测值作为输入值建立神经网络模型的主要框架，预测下一时段的输出值。通过双隐含层BP人工神经网络分析2011-2014年老哈河赤峰段甸子点位的4项污染指标的变化规律，预测2015年的数值并验证神经网络预测的准确性，表明人工神经网络用来预测老哈河赤峰段水质变化具有可行性，其中总磷具有较高的预测精度。

缺失值是影响完整性的主要因素。由于数据录入的遗漏、不正确的度量方法和数据采集条件的限制等多方面因素都有可能导致数据缺失，从而使数据不完整，更会影响后续数据挖掘、统计分析等工作的进行[16]。常规处理方法有历史均值替代缺失值、利用资料序列的前后值加权以及直接代替个别缺失值。从缺失的分布来看，缺失值可分为完全随机缺失、随机缺失和完全非随机缺失[17]。缺失值掩盖了数据的分布，干扰了属性相关性的发现，缺失值补全具有重要的理论和实践意义，是后续分析挖掘工作的基础[18]。本文可用的训练样本数量较少，应用拉格朗日插值法补充了缺失值，保证了时间序列数据的完整性，保证了模型的预测精度。

神经网络隐含层层数和模型的预测精度密切相关，隐含层较少时因获取的有效信息太少而导致预测精度较低，过多时往往会出现过拟合现象而降低预测精度，因此隐含层层数的选择对BP神经网络模型的预测能力十分重要[19-20]。一般认为针对简单的问题，单隐含层即可满足要求，但是对于复杂的问题，则需要多个隐含层才能达到较好的预测效果，同时随着隐含层的增加，网络结构复杂程度也随之增加，对数据中的噪声信号具有放大作用，从而降低模型的预测精度，因此网络隐含层层数的选择十分重要[14，20]。本文采用双层BP神经网络对老哈河水质预测取得了较好的预测精度。