麦比乌斯梯子C(2n,n)的强边色数
2018-05-21姚顺禹马登举
姚顺禹,马登举
(南通大学理学院,江苏南通 226019)
1 引言
在图G=(V(G),E(G))中,V(G),E(G)分别表示图G的顶点集合,边集合.图G的一个k-边正常染色是指一个映射f:E(G)→ {1,2,···,k},使得对于任何两个相邻的边e1,e2,均有f(e1)f(e2),图G的k-边正常染色又简称为k-边染色.设G是一个图,e1=u1v1,e2=u2v2是图G中的两条边.若e1与e2相邻,则称e1与e2的距离为0,若e1与e2不相邻,从e1的一个端点到e2的一个端点的路称为e1到e2的一条路.e1与e2的距离是指在e1到e2的所有路中一条最短路所含的边数.图G的k-强边染色是一种k-正常染色,使得任意相邻于同一条边的两条边不得染相同的颜色.换句话说,图G的强边染色是一种边染色,使得任意两条距离不大于1的边被染不同颜色.图G的强边色数(G)是最小的k,使得G有一个k-强边染色.
1985年,Erdös和Nešetil[1]给出了关于强边染色的概念,并提出了如下猜想:对于最大度为ΔG的图G,Molloy和Reed[2]证明了当ΔG足够大时,(G)≤这里 ∈约为.而Bruhn和Joos[3]进一步证明了Andersen[4]证明了一个3-正则图G的强边色数
麦比乌斯梯子C(2n,n)是这样一个图,它的顶点集为V={vi|i=1,2,···,2n},边集为E={vivi+1,vivi+n|i=1,2,···2n},这里的加法在取模2n的情况下进行.它是一个3-正则图,可以嵌入在射影平面上,当n=3时,C(2n,n)就是K3,3.本文研究了C(2n,n)的强边色数,得到如下结果:当n=3时,当当n=5,8时当n≥3且n≡2(mod 4)时,当n≥7且n≡0,1或3(mod 4)时,
2 主要结论
在本节的开始,先给出C(2n,n)的强边色数的一个下界.
当n=2时,C(2n,n)即为K4,因为K4中任意两条边之间的距离都小于2,且K4含有6条边,所以χ′s(C(4,2))=6.接下来,考虑n≥3的情形.
引理2.1当n≥3时,χ′s(C(2n,n))≥6.
证当n≥3时,C(2n,n)有一个导出子图同构于如图1所示的图H.不难发现图H中任何两条边之间的距离都不大于1.因图H 含有6条边,故(H)≥ 6,从而
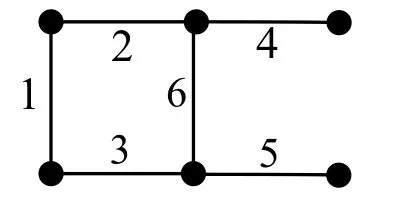
图1:图H
引理2.2当n≥3时,χ′s(C(2n,n))=6当且仅当n≡2(mod 4).
证 充分性设n≡2(mod 4),欲证χ′s(C(2n,n))=6.
由引理2.1知故只需证此时,只需给出C(2n,n)的一种只含有6种颜色的强边染色.现定义C(2n,n)的一个边染色f:E(C(2n,n))→{1,2,3,4,5,6},如下:f(vivn+i)=1(i=1,3,5···,n−1);f(vivi+1)=2(i=1,5,9,···,2n−3);f(v1v2n)=f(vivi+1)=3(i=4,8,12,···,2n−4);f(vivi+1)=4(i=3,7,11,···,2n−1);f(vivi+1)=5(i=2,6,10,···,2n − 2);f(vivn+i)=6(i=2,4,8,···,n).不难验证 f 符合强边染色的定义,所以当n≡2(mod 4)时,χ′
s(C(2n,n))≤6.
必要性设(C(2n,n))=6,欲证n≡2(mod 4).
只需证明当n2(mod 4)时,(C(2n,n))6.
当n≡ 0(mod 4)时,假设(C(2n,n))=6.此时,存在C(2n,n)的一个强边染色f:E(G)→ {1,2,3,4,5,6}.首先边v1v2,v1vn+1,v1v2n,v2v2+n,vn+1vn+2,vnvn+1中的任一条边都需要染不同的颜色,因为在这些边中任意两条边之间的距离都小于2.不妨设f(v1vn+1)=1,f(v1v2)=2,f(v1v2n)=3,f(vn+1vn+2)=4,f(vnvn+1)=5,f(v2vn+2)=6.因为v2v3与边v1v2,v1vn+1,v1v2n,v2v2+n,vn+1vn+2之间的距离都小于2,而与vnvn+1的距离等于2,所以f(v2v3)=5.同样的,f(v1v2n)=f(vn+2vn+3)=3,f(v1vn+1)=f(v3vn+3)=1,f(vn+1vn+2)=f(v3v4)=4,f(vn+3vn+4)=f(v1v2)=2,f(v4vn+4)=f(v2vn+2)=6.对剩下的边染色,每一条边只有一种颜色可染.染色规律如下
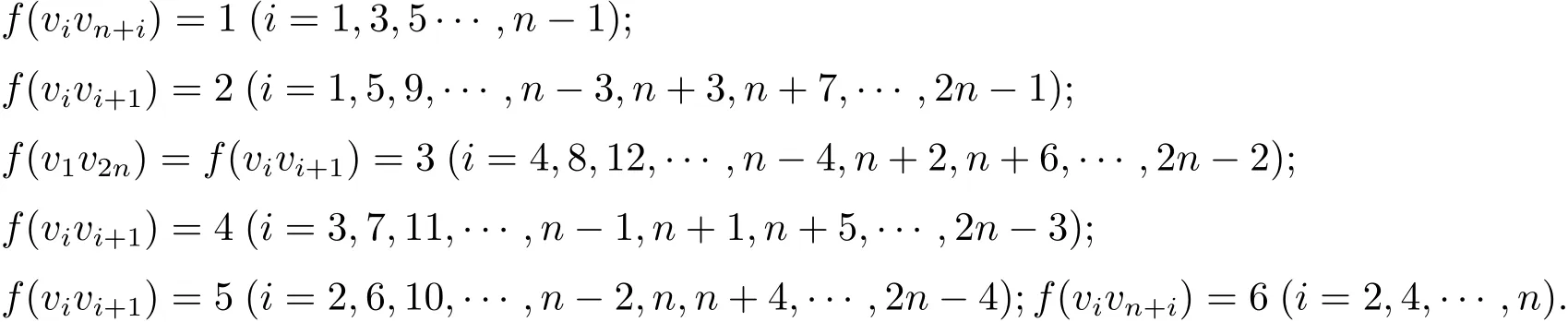
此时会发现,因为n≡0(mod 4),所以f(vn−1vn)=4,而f(vn+1vn+2)=4,但两边之间的距离为1,这与强边染色的定义相矛盾,故当n≡0(mod 4)时同理,当n≡1或3(mod 4)时,
定理2.3当n/≡2(mod 4)时,
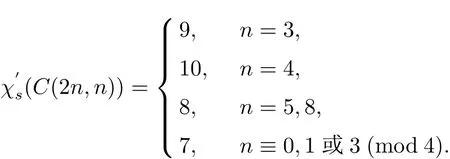
证当n=3时,在C(6,3)中,任两条边之间距离都小于2.所以一种颜色只能染一条边,又C(6,3)有9条边,所以(C(6,3))=9.
当n=4时,在C(8,4)中,圈D=v1v2v3···v8v1中任何两条边的距离都小于2.因圈D有8条边,故对圈D强边染色至少需要8种颜色.又因D中任何一边与C(8,4)中除D以外的边的距离都小于2,故染剩下的边所用的颜色和圈D所用的颜色不同.在剩下的4条边中,存在两条边之间的距离小于等于1,故剩下的4条边至少需要两种颜色.综上所述,C(8,4)进行强边染色至少需要10种颜色,即(C(8,4))≥10.现定义C(8,4)的一个边染色f:E(C(8,4)) → {1,2,···,10},如下:f(v1v2)=1,f(v2v3)=2,f(v3v4)=3,f(v4v5)=4,f(v5v6)=5,f(v6v7)=6,f(v7v8)=7,f(v8v1)=8,f(v1v5)=f(v3v7)=9,f(v2v6)=f(v4v8)=10.不难验证f是一个强边染色,即(C(8,4))≤10,所以
当n=5时,由引理2.1与2.2知(C(10,5))≥7.现假设(C(10,5))=7.则存在一个强边染色f:E(C(10,5))→{1,2,3,4,5,6,7}.为讨论方便,称圈A=v1v2v3···v10v1上的边为第一类边,其余的边为第二类边.因为圈A上任意三条边中,存在两条边使得它们之间的距离小于等于1,故当一种颜色所染的边都是第一类边时,这种颜色至多染两条边.因为第二类边的任意三条边中,存在两条边使得它们之间的距离小于等于1,故当一种颜色所染的边都是第二类边时,这种颜色至多染两条边.当一种颜色所染的边既有第一类边又有第二类边时,不妨设所用的颜色为1,且v1v2被颜色1所染,即f(v1v2)=1,此时第二类边中,只有v4v9可染与v1v2相同的颜色,那么颜色1至多可染两条边.
综上所述,任一种颜色在C(10,5)中所染的边数不能大于等于3.因为C(10,5)共有15条边,且(C(10,5))=7,所以至少存在一种颜色所染的边数要大于等于3.故产生矛盾.故现定义C(10,5)的一个边染色g:E(C(10,5))→{1,2,3,4,5,6,7,8},如下g(v1v6)=g(v4v9)=1,g(v1v2)=g(v8v9)=2,g(v1v10)=g(v7v8)=3,g(v6v7)=g(v3v4)=4,g(v5v6)=g(v3v8)=5,g(v2v7)=g(v5v10)=6,g(v4v5)=7,g(v2v3)=g(v9v10)=8.不难验证边染色g是一个强边染色,即
当n=8时,由引理2.1与2.2知现假设则存在一个强边染色f:E(C(16,8))→ {1,2,3,4,5,6,7}.为讨论方便,称圈C=v1v2v3···v16v1上的边为第一类边,其余的边为第二类边.因为圈C上任意四条边中,存在两条边使得它们之间的距离小于等于1,故当一种颜色所染的边都是第一类边时,这种颜色至多染三条边.因为第二类边的任意五条边中,存在两条边使得它们之间的距离小于等于1,故当一种颜色所染的边都是第二类边时,这种颜色至多染四条边.当一种颜色所染的边既有第一类边又有第二类边时.不妨设所用的颜色为1,且v1v2被颜色1所染.即f(v1v2)=1.此时第二类边中,f(v4v12),f(v5v13),f(v6v14),f(v7v15)可以等于1,当f(v4v12)=1时,剩下边f(v6v7),可以等于1,但这五条边中,任意两边之间的距离都小于2,故只有一条边可染与v1v2相同的颜色,故颜色1至多染三条边.故任一种颜色所染的边既有第一类边又有第二类边时,这种颜色至多能染三条边.
综上所述,任一颜色在C(16,8)中至多染四条边.此时,设x为只染第二类边的颜色数目.当x=0时,因为所以7种颜色至多染7×3=21条边.当x=1时,至多染1×4+(7−1)×3=22条边.当x=2时,至多染2×4+(7−2)×3=23条边.当x≥3时,因为只有八条第二类边,至多染8+(7−x)×3≤20条边.而C(16,8)有24条边,所以与假设矛盾.故(C(16,8))≥8,现定义C(16,8)的一个边染1,h(v1v2)=h(v11v12)=h(v6v7)=2,h(v1v16)=h(v10v11)=h(v4v5)=3,h(v3v4)=h(v9v10)=h(v14v15)=4,h(v2v3)=h(v8v9)=h(v12v13)=5,h(v2v10)=h(v4v12)=h(v6v14)=h(v8v16)=6,h(v5v6)=h(v15v16)=7,h(v7v8)=h(v13v14)=8.不难验证h是一个强边染色,即(C(16,8))≤ 8.故 χ′s(C(16,8))=8.
当n≡0(mod 4)时,由引理2.1与2.2知下面证(C(2n,n))≤7.为此先给出的一个有7种颜色的强边染色,如图2所示.而当n>12时,只需将图2中的边v6v7与vn+6vn+7(n=4k,k≥3)删除,并将点v6,vn+6,分别与图3中的点a,b粘合,并分别将点v7,vn+7与c,d之间连一条边,然后令f(c v7)=2,f(d vn+7)=4,即可得到C(2n,n)(n=4k,k>3)的强边色数.
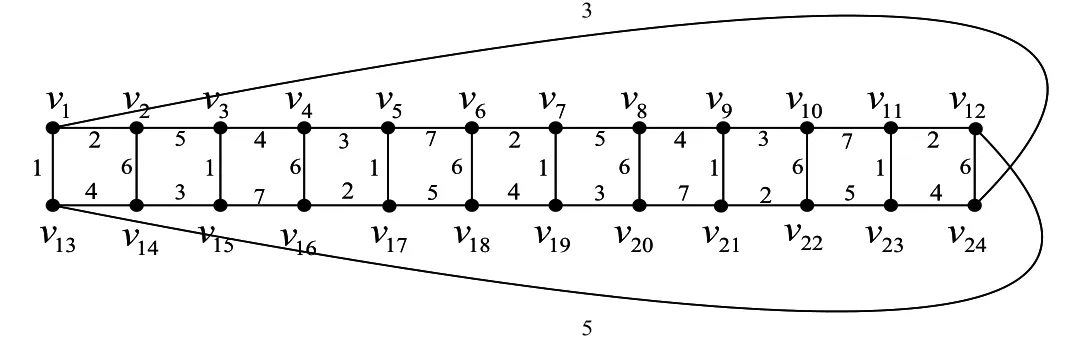
图2:当n=12时,(C(2n,n))=7
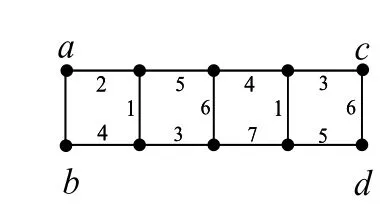
图3:嵌入部分
当n≡1(mod 4)时,由引理2.1与2.2知下面证明(C(2n,n))≤7,为此先给出C(18,9)的一个有7种颜色的强边染色.如图4所示.而当n>9时,只需将图4中的边v7v8与vn+7vn+8(n=4k+1,k≥2)删除,并将点v7,vn+7分别与图5中的点a,b粘合,并分别将点v8,vn+8与c,d之间连一条边,然后令f(c v8)=3,f(d vn+8)=5,即可得到C(2n,n)(n=4k+1,k>2)的强边色数.
当n≡3(mod 4)时,由引理2.1与2.2知下面证明为此先给出C(14,7)的一个有7种颜色的强边染色.如图6所示.而当n>7时,只需将图6中的边v6v7与vn+6vn+7(n=4k+3,k≥1)删除,并将点v6,vn+6分别与图7中的点a,b粘合,并分别将点v7,vn+7与c,d之间连一条边,然后令f(c v7)=2,f(d vn+7)=4,即可得到C(2n,n)(n=4k+3,k>1)的强边色数.
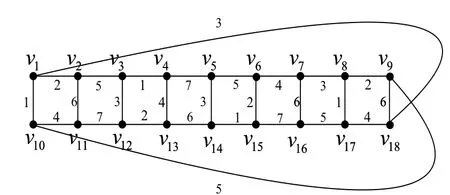
图4:当n=9时,(C(2n,n))=7
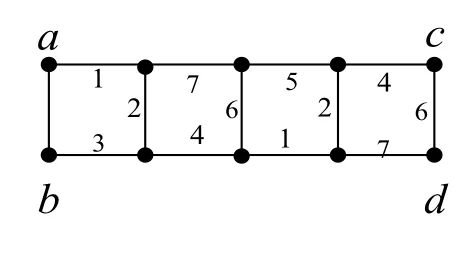
图5:嵌入部分

图6:当n=7时,(C(2n,n))=7
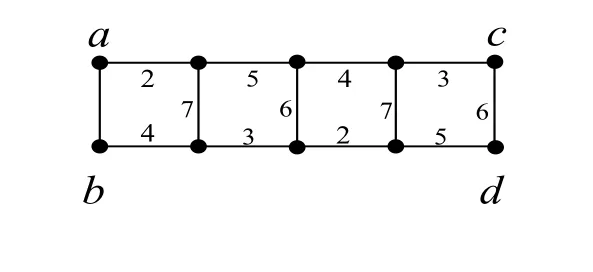
图7:嵌入部分
参考文献
[1]Erdös P.Problems and results in combinatorial analysis and graph theory[J].Ann.Disc.Math.,1988,38:81–92.
[2]Molloy M,Reed B.A bound on the strong chromatic index of a graph[J].J.Comb.The.,Ser.B,1997,69(2):103–109.
[3]Bruhn H,Joos F.A stronger bound for the strong chromatic index[J].Elec.Notes Disc.Math.,2015,49:277–284.
[4]Andersen L D.The strong chromatic index of a cubic graph is at most 10[J].Disc.Math.,1992,108(1-3):231–252.
