分数布朗随机流
2018-05-21肖艳萍郭精军
肖艳萍,郭精军
(1.西北民族大学数学与计算机科学学院,甘肃兰州 730000)
(2.兰州财经大学统计学院,甘肃兰州 730020)
1 引言
近些年,分数布朗运动因具有自相似性、长相依性等特点被广泛地应用于金融、通信等领域,已成为随机分析及其相关领域研究的热点问题之一.但是,当Hurst参数时,分数布朗运动既不是半鞅,也不是马尔科夫过程.于是,随机分析中一些经典的方法就不能直接拿来处理分数布朗运动相关问题了.
流概念源于几何测度理论.最简单的形式为如下泛函
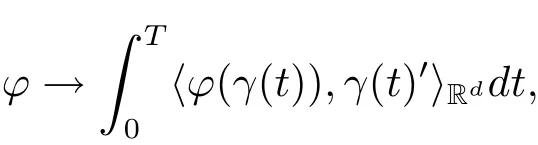

基于文献[6,8],本文利用白噪声分析方法研究Wick积分意义下的分数布朗随机流.行文安排如下:在第2部分中主要介绍分数布朗运动和白噪声分析框架的一些基本事实;在第3部分,先给出Wick型分数布朗随机流的定义,其次借助于解析刻画定理证明分数布朗随机流在白噪声分析框架下是一个广义泛函.
2 预备知识
该部分主要介绍分数布朗运动、白噪声分析框架及一些相关结果,详细内容见文献[2,7–8].
定义2.1[1−2]如果{BH(t)}t∈R是一个中心高斯过程且有
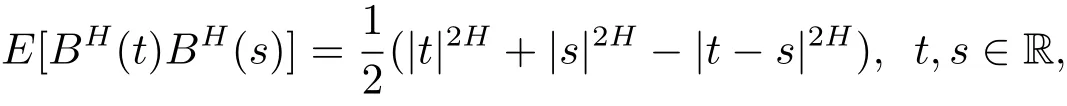
称随机过程{BH(t)}t∈R为分数布朗运动.
为了获得BH(t)的表示形式,需要利用分数积分算子和微分算子,α∈(0,1).如果定义
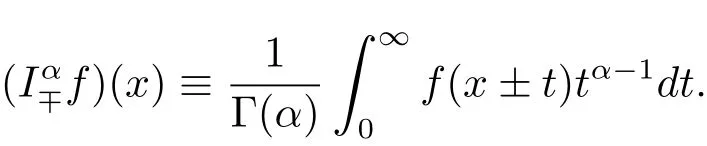
如果定义


定义2.2[1−2]假设0<H<1,算子MH±定义为
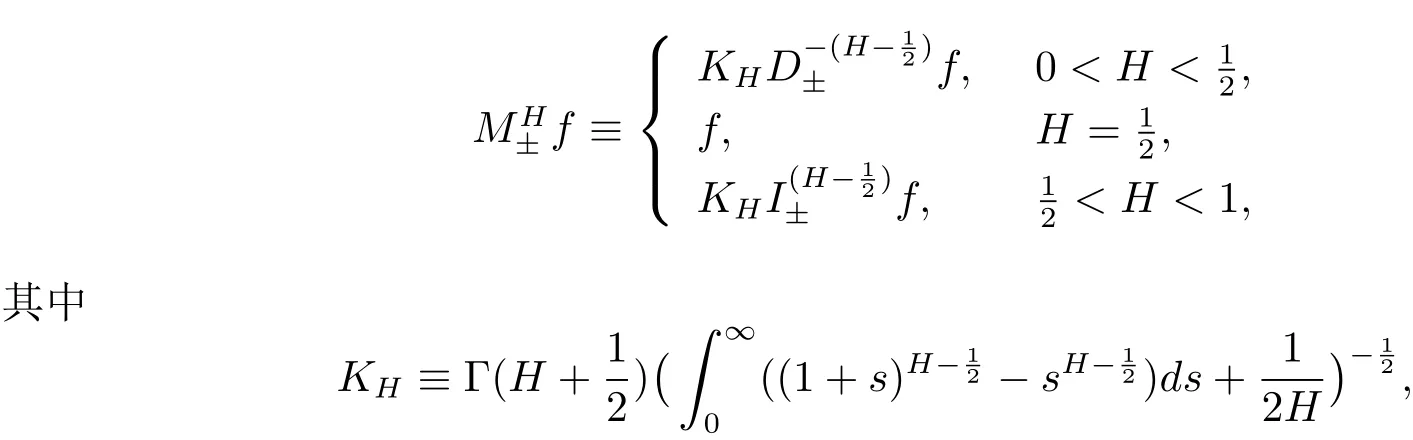
则分数布朗运动有连续版本
第一组Gelfand三元组为S(R)⊂ L2(R,Rd)⊂ S∗(R),其中S(R)和S∗(R)分别为Schwartz向量值检验泛函空间和缓增函数空间.
设(L2)≡L2(S∗(R),dµ)为S∗(R)上关于µ平方可积泛函所构成的希尔伯特空间.则由Wiener-Itô-Segal同构定理知,对每个f∈(L2)有以下混沌表示
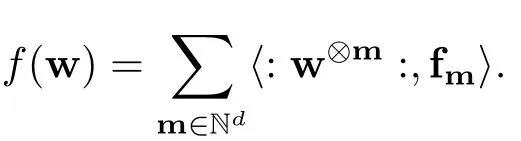
设Γ(A)是A的二次量子化算子,其中A定义如下

对每个整数关于希尔伯特范数完备化空间.从而,设分别为的投影极限和归纳极限.于是,第二组Gelfand三元组为(S)⊂(L2)⊂(S)∗.(S)(相应地,(S)∗)中元素称之为Hida检验泛函(相应地,广义泛函).
对所有的检验泛函f∈S(R,Rd),在(S)×(S)∗上定义S-变换如下

引理2.3[7−9]设{Gk}k∈N表示U-泛函序列:
(1)对f∈S(R),{Gk(f)}k∈N是一个柯西列;
(2)存在Ci和p使得在R中一致有则存在唯一Φ∈(S)∗使得S−1Gk强收敛于Φ.
引理2.4[7−9]设(Ω,B,µ)是一个可测空间以及在Ω上定义取值于(S)∗的一个映射为Φλ.假设Φλ的S-变换满足
(1)对所有的f∈S(R,Rd),是关于λ的µ-可测函数;
(2)服从 U-泛函估计对固定的 p和对C1∈ L1(µ),C2∈ L∞(µ)成立,
从而Φλ在希尔伯特空间(S)−q中当q足够大时是Bochner可积的,
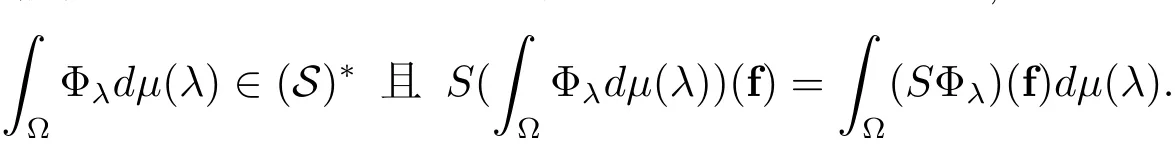
3 分数布朗随机流
因为存在非适应性积分,在定义分数布朗随机流时,需要考虑随机积分的处理难易性以及如何给出合理的解释.在该部分中,首先给出Wick积分意义下的分数布朗随机流的定义;其次讨论该随机流的存在性问题.
定义3.1设ϕ:Rd→Rd定义在由所有光滑紧支撑向量域构成的集合上,则
在倡导可持续发展的观念之下,绿色建筑从建筑业中脱颖而出。相比于传统建筑物而言,绿色建筑不仅可以节约水、煤气、木材等自然资源,减少环境污染,而且也可以营造亲近自然、舒适健康的居住氛围,使居民身心得到舒展。

是一个泛函.Wick型分数布朗随机流定义为

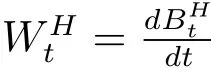
利用定义3.1可以证明:分数布朗随机流在白噪声分析框架下是一个Hida广义泛函.
定理3.2对每个正整数d,每个H∈(0,1)和ε>0,分数布朗随机流



证对任意f∈S(R),首先验证引理2.4中可积性条件满足.计算S-变换

由文献[1]中的引理2.5,定理2.3以及推论2.8,对f∈S(R),有

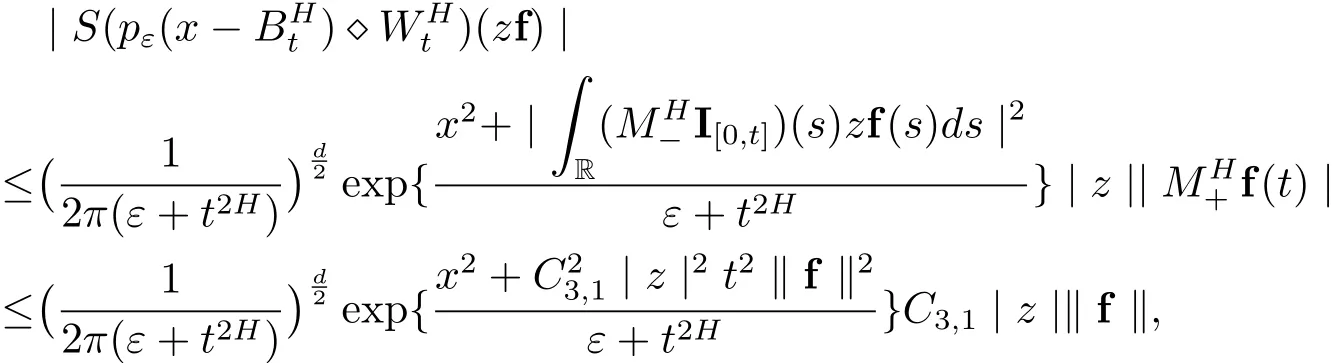


定理3.3对每个H∈(0,1)和d≥1,Bochner积分

和

都是Hida广义泛函.进一步,当ε趋于0时,ξH,ε(x)在(S)∗中收敛到ξH(x).



则对所有的z∈C,有

最后一个等式在Rd上关于λ可积,同时第二部分关于λ是一个常数.


由控制收敛定理知,当ε趋于0时,S(ξH,ε(x))(f)收敛于S(ξH(x))(f).由引理2.3知,当ε趋于 0 时,ξH,ε(x) 收敛到 ξH(x).
文献[6]利用Malliavin计算讨论了Skorohod积分意义下的布朗和分数布朗随机流.相比较Malliavin计算白噪声分析方法在某种程度上将更方便,因为此时可以利用白噪声分析方法方便地处理随机积分问题.同时所获得的结果对Hurst指数的要求更加宽泛,正则性条件也有别于文献[6]中的条件:对时,分数布朗随机流属于Sobolev空间的条件是
参考文献
[1]Bender C.An Itô formula for generalized functionals of a fractional Brownian motion with arbitrary Hurst parameter[J].Stoc.Proc.Their Appl.,2003,104:81–106.
[2]Biagini F,Hu Y Z,Øksendal B,Zhang T S.Stochastic calculus for fractional Brownian motion and applications[M].London:Springer-Verlag,2008.
[3]Flandoli F.On a probabilistic description of small scale structures in 3D fluids[J].Ann.Inst.H.Poin.Prob.Stat.,2002,38:207–228.
[4]Flandoli F,Gubinelli M,Giaquinta M.Stochastic currents[J].Stoc.Proc.Their Appl.,2005,115:1583–1601.
[5]Flandoli F,Gubinelli M,Russo F.On the regularity of stochastic currents,fractional Brownian motion and applications to a turbulence model[J].Ann.Inst.H.Poin.Prob.Stat.,2009,45(2):545–576.
[6]Flandoli F,Tudor C A.Browinan and fractional Brownian stochastic currents via Malliavin calculus[J].J.Func.Anal.,2010,258:279–306.
[7]Obata N.White noise calculus and Fock space[M].Lect.Notes Math.,Berlin:Springer-Verlag,1994.
[8]Oliveira M,Silva J,Streit L.Intersection local times of independent fractional Brownian motions as generalized white noise functionals[J].Acta Appl.Math.,2011,113:17–39.
[9]Guo Jingjun,Li Chujin.On collision local time of two independent fractional Ornstein-Uhlenbeck processes[J].Acta Math.Sci.Ser.B,2017,37(2):316–328.
[10]Guo Jingjun,Jiang Guo,Xiao Yanping.Multiple intersection local time of fractional Brownian motion[J].J.Math.,2011,31(3):388–394.
