素超代数的广义超导子和局部广义超导子

袁鹤

(吉林师范大学数学学院,吉林四平 136000)

1 引言

设A是代数,若A上的线性映射d满足对于任意a∈A存在导子da:A→A使得d(a)=da(a),则称d是A上的局部导子.Kadison[1]与Larson和Sourour[2]最先开始研究局部导子,他们得到一些特殊的代数上的局部导子是导子.Brešar[3]证明了含有非平凡幂等元的素环上的局部导子是导子.Fošner[4]将Brešar[3]的结果推广到了超代数上.1991年,Brešar[5]给出了环上广义导子的定义:若对于环R上的加法映射g存在R上导子d满足g(xy)=g(x)y+xd(y),x,y∈R,则称g是R上的广义导子.王宇[6]研究了含有非平凡幂等元的素环上的Brešar意义下的局部广义导子.2015年,赵延霞等[7]研究了可换环上上三角矩阵李代数的局部自同构和局部导子.

Nakajima在文献[8]中还引入了另一种广义导子.设A是代数,m∈A,g:A→A是线性映射,如果

则称(g,m)是A上的广义导子.特别地,若A含有单位元1,则m=−g(1).Fošner[9]研究了由幂等元生成的代数上的Nakajima意义下的局部广义(α,β)-导子.

根据Nakajima意义下的广义导子的定义,我们给出了广义超导子和局部广义超导子的定义.证明了具有非平凡幂等元的素超代数上的局部广义超导子均为广义超导子,还给出了广义超导子的一个刻画.

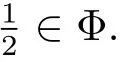
定义1.1设A是超代数且i∈{0,1}.若m∈Ai与i阶线性映射g:A→A满足

则称(g,m)是A上i阶的广义超导子.一个0阶广义超导子与一个1阶广义超导子之和称为A上的广义超导子.

若A含有单位元1,则上述定义中的m=−g(1).显然,g(xy)=g(x0y0)+g(x0y1)+g(x1y0)+g(x1y1),其中x=x0+x1,y=y0+y1.根据环上Brešar意义下的广义导子的定义,本文作者[10]给出了超代数上Brešar意义下的广义超导子的定义.

定义1.2设A是超代数,g:A→A是i阶线性映射,若存在A上i阶的超导子d满足

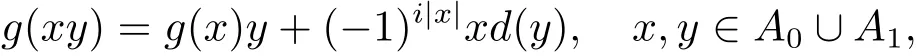
则称g是A 上i阶的Brešar型广义超导子.若g=g0+g1,其中gi是A上i阶的Brešar型广义超导子,则称g是A上的Brešar型广义超导子,称d=d0+d1是g的相伴超导子.

实际上,Nakajima型广义超导子均为Brešar型广义超导子.定义映射d=g+λa,其中λa(x)=mx,所以d(s)=g(s)+ms,s∈H(A).因此对于任意s,t∈H(A),

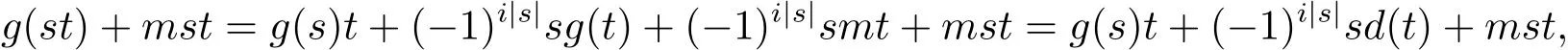
所以g(st)=g(s)t+(−1)i|s|sd(t).又因为

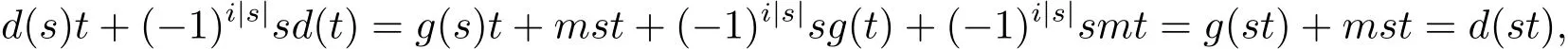
所以d是A上i阶的超导子.

定义1.3设A是超代数且i∈{0,1}.若i阶线性映射g:A→A满足对于任意x∈A存在i阶的广义超导子(gx,m):A→A使得g(x)=gx(x),则称g是A上i阶的局部广义超导子.一个0阶局部广义超导子与一个1阶局部广义超导子之和称为A上的局部广义超导子.

设A=A0⊕A1是超代数,定义集合E=E0⊕E1,其中E0={e∈A0|e2=e}(E0是A0中所有幂等元构成的集合),E1={e∈A1|存在e′∈E0满足(e′+e)2=e′+e}.因为(e′+e)2=e′+e,e′∈ E0,e ∈ E1,所以 e2=0,e′e+ee′=e.用 R=R0⊕R1来表示由 E 生成的A 的子超代数,用I=I0⊕I1来表示由[E0,A]生成的A 的分次理想,其中[·,·]表示换位子.由文献[4,引理1.2],I⊆R.如无特殊说明,本文中的A是指含有单位元和非平凡幂等元的素超代数.显然,I0.对于A的元素,我们将用带下标的同一字母表示该元素的齐次分量,例如若x∈A,则其0次和1次齐次分量分别记作x0和x1.

2 局部广义超导子

本节将证明A上的局部广义超导子是广义超导子.

引理2.1设g是A上i阶的局部广义超导子,则

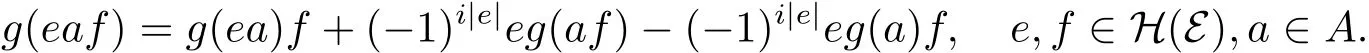
证因为g是A上i阶的局部广义超导子,i∈{0,1},所以对于任意y∈A,x∈H(A),z∈A,存在i阶的广义超导子(gy,m)满足

现在断言,对于任意x,y∈A,若xy=yz=0,则必有(x0+(−1)ix1)g(y)z=0.实际上,由可得x0y0+x1y1=x0y1+x1y0=0,从而

设e,f是A中的幂等元,则对于任意a∈A均有

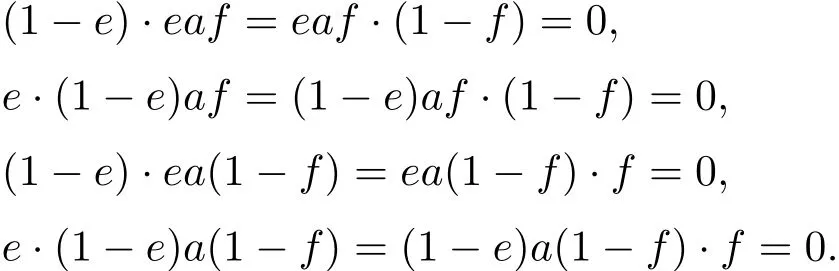
因此,对于e0∈E0,f0∈E0,根据上面的断言可得

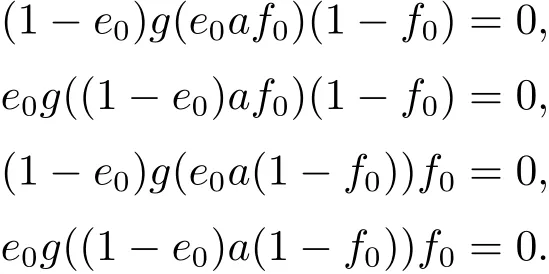
因此

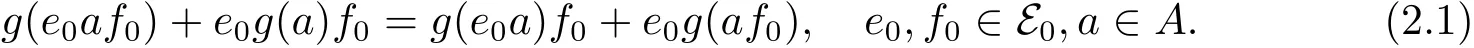
对于e0∈E0,f=f0+f1∈E,f0∈E0,f1∈E1,再由上面的断言可得

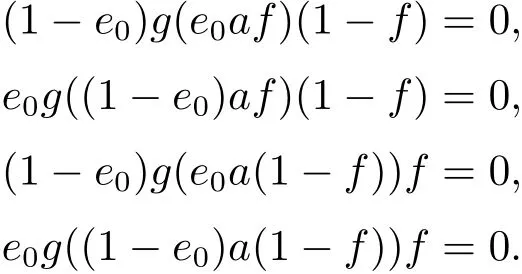
因此

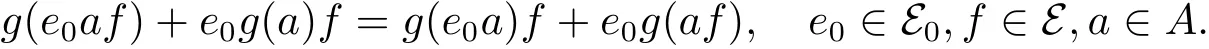
再由(2.1)式有

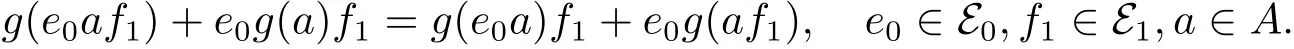
类似地,对于任意f0∈E0,e1,f1∈E1,a∈A,有

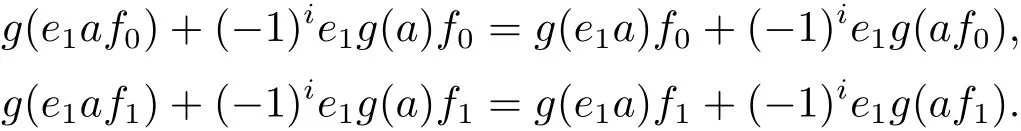
因此g满足

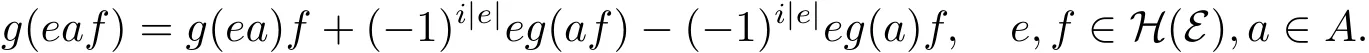
引理2.2设g是A上i阶的局部广义超导子,则

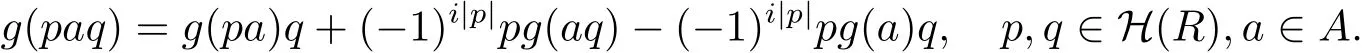
证只需证明对于任意e1,···,em,f1,···,fn∈ H(E)均有

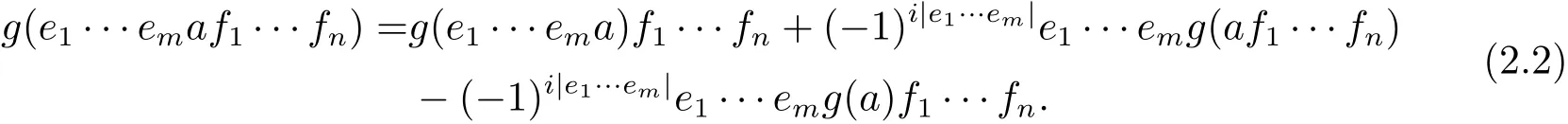
先假设m=1.现在对n用数学归纳法.显然当n=1时,(2.2)式成立.假设(2.2)式对于n成立.那么

因此当m=1时,(2.2)式对于任意n都成立.下面对m用数学归纳法.已经证明当m=1时,(2.2)式成立.现在假设(2.2)式对于m成立.那么因此(2.2)式对于任意m,n都成立.

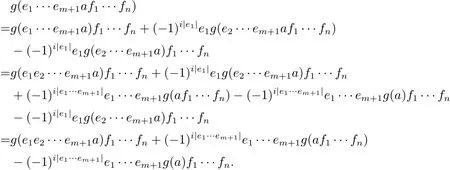
引理2.3设A是含有单位元和非平凡幂等元的素超代数,若g是A上i阶的局部广义超导子,则(g,g(1))是A上i阶的广义超导子.

证在引理2.2中,取a=1有

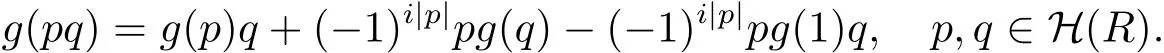
因为I⊆R,所以

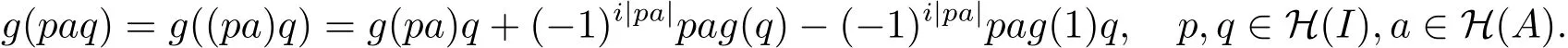
又因为

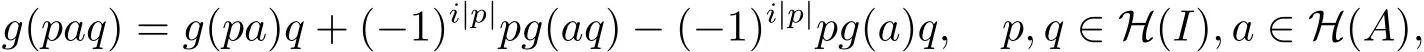
所以上面两式相减有

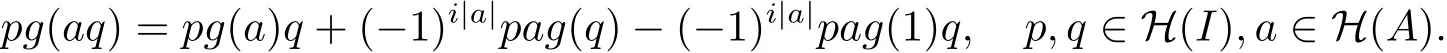
因为p∈H(I),所以

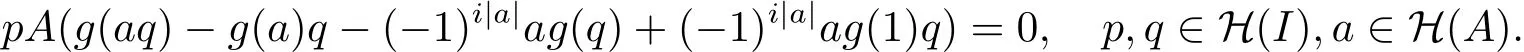
因为A是素超代数,所以

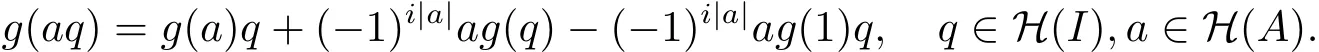
用两种不同的方式展开g(abq),对于任意q∈H(I),a,b∈H(A),有

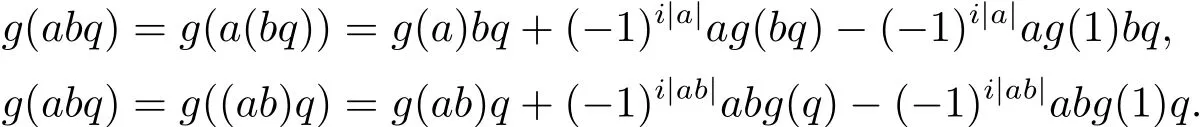
两式相减有

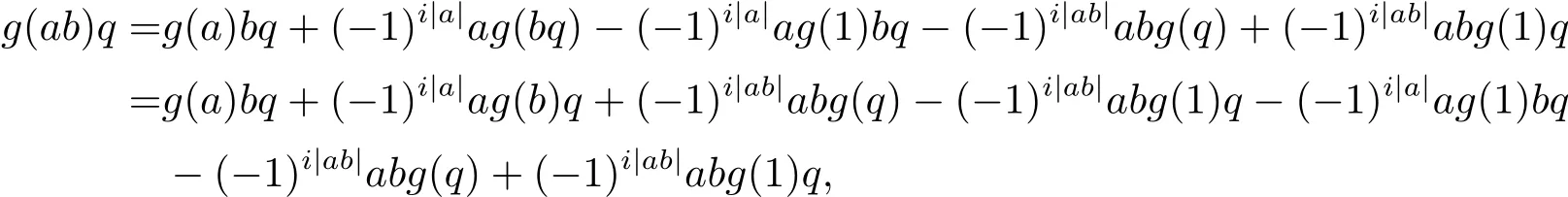
因此

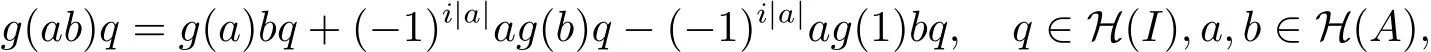
整理有

因为q∈H(I),所以

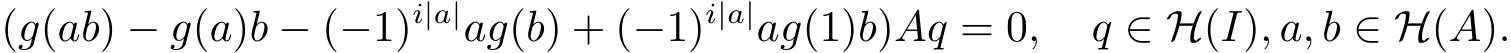
因为A是素超代数,所以

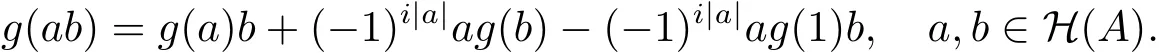
因此(g,g(1))是A上i阶的广义超导子.

由上面这个引理有

定理2.4设A是含有单位元和非平凡幂等元的素超代数,A上的局部广义超导子是广义超导子.

3 广义超导子

定理3.1设A是具有非平凡幂等元的素超代数,g:A→A是i阶线性映射,m∈Ai,则(g,m)是i阶的广义超导子的充分必要条件是对于任意的x,y∈A,当xy=0时,

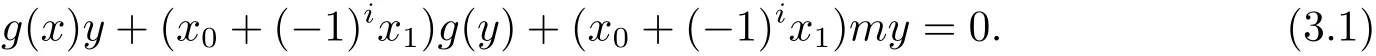
显然,A上i阶的广义超导子满足上式.本节主要是证明充分性.为了方便,设

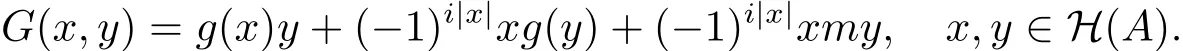
引理3.2G(xr,z)=G(x,rz), x,z∈H(A),r∈H(R).

证设e是A中的幂等元,任取x,z∈H(A),因为

所以对于e0∈E0,由(3.1)式可得

两式相减有

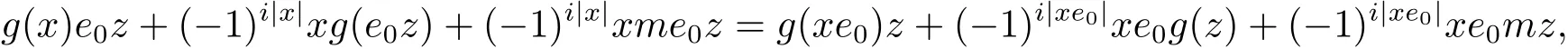
即G(x,e0z)=G(xe0,z).再由(3.1)式,对于任意x,z∈H(A),有

其中e=e0+e1.两式相减有

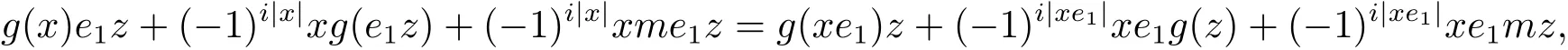
即G(x,e1z)=G(xe1,z).因此对于任意e∈H(E)有G(x,ez)=G(xe,z).设T={r∈H(A)|G(xr,z)=G(x,rz),x,z∈H(A)}.因为对于任意r,r′∈T,x,z∈H(A),有

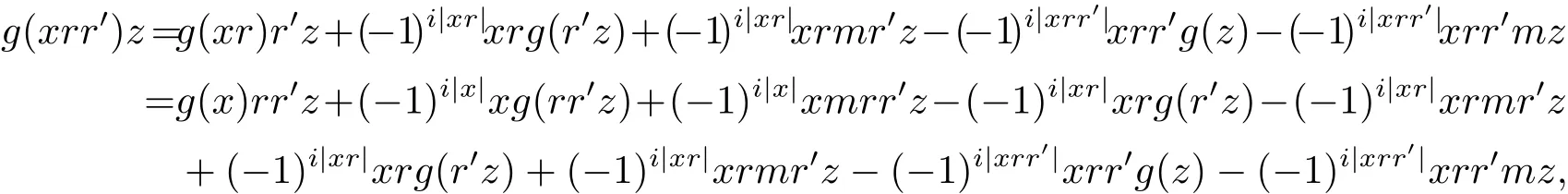
所以rr′∈T.因为H(E)⊆T,所以H(R)⊆T,即对于任意r∈H(R),有G(xr,z)=G(x,rz).

引理3.3映射g满足对于任意t∈H(A2I),x,y,z,w∈H(A),有

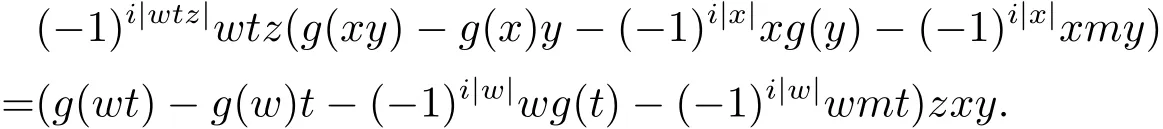
证设 u ∈ H(I),x,y,z,w,w′,w′′∈ H(A),则 uzx,w′′uz,w′w′′u ∈ H(I)⊆ H(R). 由引理3.2,有

设t=w′w′′u,显然t∈H(A2I).因此对于任意x,y,z,w∈H(A)有

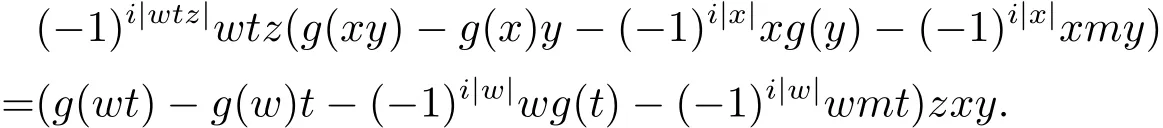
引理3.4设g是A上满足(3.1)式的0阶线性映射,则(g,m)是A上0阶的广义超导子.

证显然A2I0.取w∈H(A),t∈H(A2I)满足wt0.由引理3.3,有

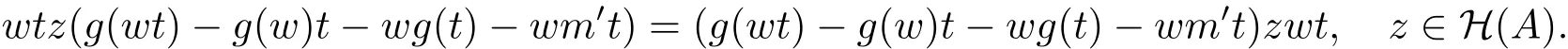
由文献[11,引理3.2],存在µ∈C0满足µwt=g(wt)−g(w)t−wg(t)−wm′t.由引理3.3,有

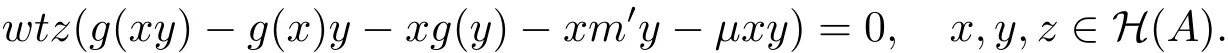
因为A是素超代数,所以

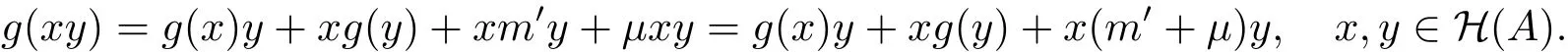
显然,m′+µ∈A0.令m=m′+µ,则(g,m)是A上0阶的广义超导子.

引理3.5设g是A上满足(3.1)式的1阶线性映射,则(g,m)是A上1阶的广义超导子.

证取w∈H(A),t∈H(A2I)满足wt0.

当C1=0时,由引理3.3和文献[11,定理3.5(i)],有

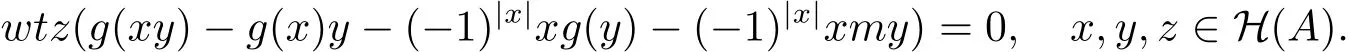
因为A是素超代数,所以

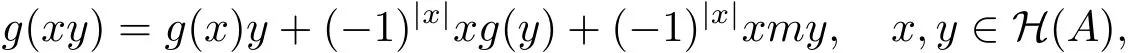
因此(g,m)是A上1阶的广义超导子.

当C10时,由引理3.3,对于任意x,y∈H(A),z0∈A0,有

由文献[11,定理3.5(ii)],对于任意z1∈A1上式也成立,即

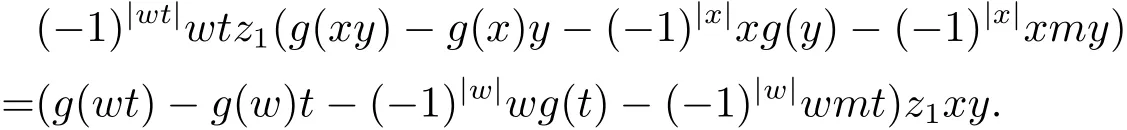
再由引理3.3,对于任意x,y∈H(A),z1∈A1,有

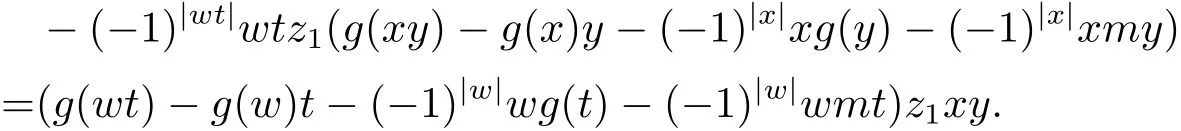
两式相减有

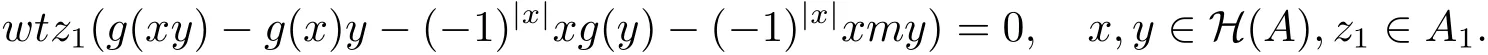
类似地,对于任意z0∈A0,有

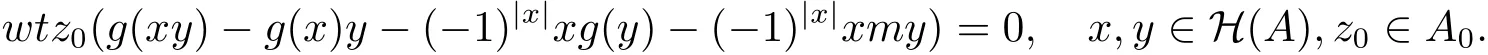
两式相加有

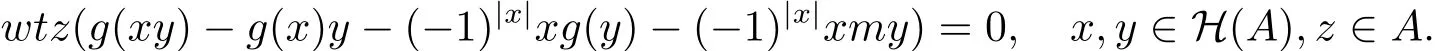
因为A是素超代数,所以g(xy)=g(x)y+(−1)|x|xg(y)+(−1)|x|xmy,x,y∈H(A).因此(g,m)是A上1阶的广义超导子.

参考文献

[1]Kadison R V.Local derivations[J].J.Alg.,1990,130(2):494–509.

[2]Larson D,Sourour A R.Local derivations and local automorphisms of B(X)[J].Proc.Symp.Pure.Math.,1990,51:187–194.

[3]Brešar M,Larson D,Sourour A R.Characterizing homomorphisms,derivations,and multipliers in rings with idempotents[J].Proc.Royal.Soc.Edinburgh,2007,137A:9–21.

[4]Fošner A,Fošner M.On superderivations and local superderivations[J].Taiwanese J.Math.,2007,11(5):1383–1395.

[5]Brešar M.On the distance of the composition of two derivations to the generalized derivations[J].Glasg.Math.J.,1991,33:89–93.

[6]Wang Y.Local generalized derivations in prime rings with idempotents[J].Alg.Coll.,2010,17(2):295–300.

[7]赵延霞,王丽.可换环上上三角矩阵李代数的局部自同构和局部导子[J].数学杂志,2015,35(5):1042–1052.

[8]Nakajima A.On categorical properties of generalized derivations[J].Sci.Math.,1999,2(3):345–352.

[9]Fošner A.Local generalized(α,β)-derivations[J].Sci.World J.,2014,2014:1–5.

[10]Yuan H,Wang Y.The product of generalized superderivations on a prime superalgebra[J].Hacet.J.Math.Stat.,2014,43(6):1009–1015.

[11]Fošner M.On the extended centroid of prime associative superalgebras with applications to superderivations[J].Comm.Alg.,2004,32(2):689–705.