SKEW CYCLIC AND LCD CODES OVER Fq+uFq+vFq
2018-05-21LIHuiHUPengLIUXiusheng
LI Hui,HU Peng,LIU Xiu-sheng
(School of Mathematics and Physics,Hubei Polytechnic University,Huangshi 435003,China)
1 Introduction
Cyclic codes over finite rings are important class from a theoretical and practical viewpoint.It was shown that certain good nonlinear binary codes could be found as images of linear codes over Z4under the Gray map(see[1]).In[2],Zhu et al.studied constacyclic codes over ring F2+vF2,where v2=v.We in[3]generated ring F2+vF2to ring F2+uF2+vF2,where v2=v,u2=0,uv=vu=0,and studied the structure of cyclic of an arbitrary length n over this ring.
Boucher et al.in[4]initiated the study of skew cyclic codes over a noncommutative ring Fq[x,Θ],called skew polynomial ring,where Fqis a finite field and Θ is a field automorphism of Fq.Later,in[5],Abualrub and Seneviratne investigated skew cyclic codes over ring F2+vF2with v2=v.Moreover,Gao[6]and Gursoy et al.[7]presented skew cyclic codes over Fp+vFpand Fq+vFqwith different automorphisms,respectively.Recently,Yan,Shi and Sol`e in[8]investigated skew cyclic codes over Fq+uFa+vFq+vFq.
In this work,let R denote the ring Fq+uFq+vFqwhere u2=u,v2=v and uv=vu=0.In Section 2,we give some properties of ring R and de fine the Gray map ϕ from R to F3q.Moreover,we investigate some results about linear codes over R.In Section 3,we first give a sufficient and necessary condition which a code C is a skew cyclic code over R.We then characterize the generator polynomials of skew cyclic codes and their dual over R.Finally,in Section 4,we address the relationship of LCD codes between R and Fq.By means of the Gray map from R to,we obtain that Gray images of LCD codes over R are LCD codes over Fq.
2 Linear Codes Over R
The ring R is a finite commutative ring with characteristic p and it contains three maximal ideals which are

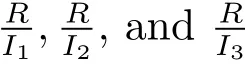
Let Rn={x=(x1,···,xn)|xj∈ R}be R-module.A R-submodule C of Rnis called a linear code of length n over R.We assume throughout that all codes are linear.
Let x,y∈Rn,the Euclidean inner product of x,y is de fined as follows
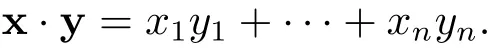
We call C⊥={x∈Rn|x·c=0,∀c∈C}as the dual code of C.Notice that C⊥is linear if C is linear or not.
In[8],it was proved that for any linear code C over a finite Frobenius ring,

The Gray map ϕ :is de fined by ϕ(x)=(β(x1),···,β(xn))for x=(x1,···,xn),where β(a+ub+vc)=(a,a+b,a+c)for a+ub+vc ∈ R with a,b,c ∈ Fq.By using this map,we can de fine the Lee weight WLand Lee distance dLas follows.
De finition 2.1For any element x=(x1,···,xn)∈ Rn,we de fine WL(x)=WH(ϕ(x)),where WHdenotes the ordinary Hamming weight for codes over Fq.The Lee distance dL(x,y)between two codewords x and y is the Lee weight of x−y.
Lemma 2.2The Gray map ϕ is a distance-preserving map from(Rn,Lee distance)to(F3n,Hamming distance)and also Fq-linear.
ProofFrom the de finition,it is clear that ϕ(x−y)= ϕ(x)− ϕ(y)for x and y ∈ Rn.Thus dL(x,y)=dH(ϕ(x),ϕ(y)).
For any x,y ∈ Rn,a,b ∈ Fq,from the de finition of the Gray map,we have ϕ(ax+by)=aϕ(x)+bϕ(y),which implies that ϕ is an Fq-linear map.
The following theorem is obvious.
Theorem 2.3If C is a linear code of length n over R,size qkand Lee distance dL,then ϕ(C)is a linear code over Fqwith parameters[3n,k,dL].
Theorem 2.4If C is a linear code of length n over R,then ϕ(C⊥)= ϕ(C)⊥.Moreover,if C is a self-dual code,so is ϕ(C).
ProofLet x1=a1+ub1+vc1,x2=a2+ub2+vc2∈C be two codewords,where a1,b1,c1,a2,b2,c2∈,and·be the Euclidean inner product on Rnor.Then and

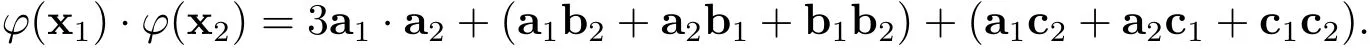
It is easy to check that x1·x2=0 implies ϕ(x1)·ϕ(x2)=0.Therefore

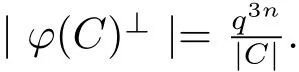

Combining(2.2)with(2.3),we get the desired equality.

Now,we mainly consider some familiar structural properties of a linear code C over R.The proof of following results can be found in[10],so we omit them here.
Let Ai(i=1,2,3)be codes over R.We denote
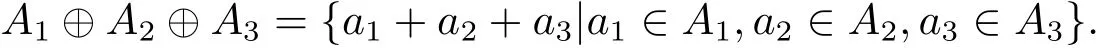
If C is a linear code of length n over R,we de fine that

It is easy to verity that Ci(i=1,2,3)are linear codes of length n over Fq.Furthermore,C=e1C1⊕e2C2⊕e3C3and|C|=|C1||C2||C3|.Throughout this paper,Ci(i=1,2,3)will be reserved symbols referring to these special subcodes.
According to above de finition and[10],we have the following theorem.
Theorem 2.5If C=e1C1⊕e2C2⊕e3C3is a linear code of length n over R,then
The next theorem gives a computation for minimum Lee distance dLof a linear code of length n over R.
Theorem 2.6If C=e1C1⊕e2C2⊕e3C3is a linear code of length n over R,then dL(C)=min{dH(C1),dH(C2),dH(C3)}.
ProofBy Theorem 2.3,we have dL(C)=dH(ϕ(C)).
For any codeword x,it can be written as x=e1a+e2b+e3c,where a∈C1,b∈C2,c∈C3.Thus

This means that dL(C)=min{dH(C1),dH(C2),dH(C3)}.
3 Skew Cyclic Codes Over R
Let R=Fq+uFq+vFq,where q=pm,p is a prime.For integer 0≤s≤m,we consider the automorphisms
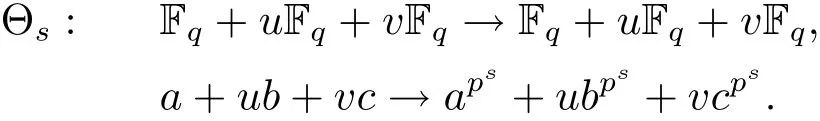
In this section,we first de fine skew polynomial rings R[x,Θs]and skew cyclic codes over R.Next,we investigate skew cyclic codes over R through a decomposition theorem.
De finition 3.1We de fine the skew polynomial ring as R[x,Θs]={a0+a1x+ ···+,where the coefficients are written on the left of the variable x.The addition is the usual polynomial addition and the multiplication is de fined by the rule xa=Θs(a)x(a∈R).
It is easy to prove that the ring R[x,Θs]is not commutative unless Θsis the identity automorphism on R.
De finition 3.2A linear code C of length n over R is called skew cyclic code if for any codeword c=(c0,c1,···,cn−1) ∈ C,the vector Θs(c)=(Θs(cn−1),Θs(c0),···,Θs(cn−2))is also a codeword in C.
The following theorem characterizes skew cyclic codes of length n over R.
Theorem 3.3Let C=e1C1⊕e2C2⊕e3C3be a linear code of length n over R.Then C is a skew cyclic code of length n over R if and only if C1,C2and C3are skew cyclic codes of length n over Fq,respectively.
ProofSuppose that xi=e1ai+e2bi+e3ci,where ai,bi,ci∈ Fq,i=0,1,···,n − 1,and x=(x0,x1,···,xn−1).Then

Set a=(a0,a1,···,an−1),b=(b0,b1,···,bn−1),c=(c0,c1,···,cn−1),thus x=e1a+e2b+e3c and a∈C1,b∈C2,c∈C3.If C is a skew cyclic code of length n over R,then
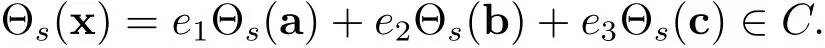
Therefore Θs(a)∈ C1,Θs(b)∈ C2,Θs(c)∈ C3.This means that C1,C2and C3are skew cyclic codes.
Conversely,if Ciare skew cyclic codes over Fq,then
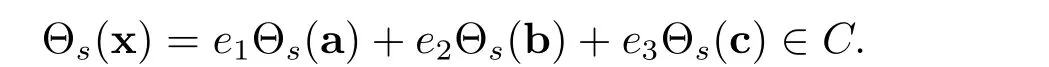
This implies that C is a skew cyclic code over R.
Theorem 3.4Let C=e1C1⊕e2C2⊕e3C3be a skew cyclic code of length n over R.Then

(2)There is a unique polynomial g(x)such that C= 〈g(x)〉and g(x)|xn− 1,where g(x)=e1g1(x)+e2g2(x)+e3g3(x).Moreover,every left submodule of R[x,Θs]/〈xn− 1〉is principally generated.
Proof(1)Since Ci= 〈gi(x)〉⊂ Fq[x,Θs]/〈xn−1〉for i=1,2,3 and C=e1C1⊕e2C2⊕e3C3,C= 〈c(x)|c(x)=e1f1(x)+e2f2(x)+e3f3(x),fi(x)∈ Ci,i=1,2,3〉.Thus
On the other hand,for any e1r1(x)g1(x)+e2r2(x)g2(x)+e3r3(x)g3(x)∈ 〈e1g1(x),e2g2(x),e3g3(x)〉⊂ R[x,Θs]/〈xn− 1〉,where r1(x),r2(x)and r3(x)∈ R[x,Θs]/〈xn− 1〉,there exist
s1(x),s2(x)and s3(x)∈ Fq[x,Θs]/〈xn− 1〉such that e1r1(x)=e1s1(x),e2r2(x)=e2s2(x)and e3r3(x)=e3s3(x).Hence

which implies that〈e1g1(x),e2g2(x),e3g3(x)〉⊂ C.Therefore C= 〈e1g1(x),e2g2(x),e3g3(x)〉.
(2)Obviously,〈e1g1(x)+e2g2(x)+e3g3(x)〉⊂ 〈e1g1(x),e2g2(x),e3g3(x)〉.
Note that e1g(x)=e1g1(x),e2g(x)=e2g2(x)and e3g(x)=e3g3(x),we have C ⊂ 〈g(x)〉.Therefore,C= 〈g(x)〉.
Since g1(x),g2(x)and g3(x)are monic right divisors of xn−1,there exist h1(x),h2(x)and h3(x)∈ Fq[x,Θs]/〈xn−1〉such that xn−1=h1(x)g1(x)=h2(x)g2(x)=h3(x)g3(x).Therefore xn−1=[e1h1(x)+e2h2(x)+e3h3(x)]g(x).It follows that g(x)|xn−1.The uniqueness of g(x)can be followed from that of g1(x),g2(x)and g3(x).
Let g(x)=g0+g1x+···+gkxkand h(x)=be polynomials in Fq[x,Θs]such that xn−1=h(x)g(x)and C be the skew cyclic code generated by g(x)in Fq[x,Θs].Then the dual code of C is a skew cyclic code generated by the polynomial
Corollary 3.5Let C1,C2,C3be skew cyclic codes of length n over Fqand g1(x),g2(x),g3(x)be their generator polynomials such that

in Fq[x,Θs].If C=e1C1⊕e2C2⊕e3C3,then
(1)is also a skew cyclic code of length n over R,where
(2)C is a self-dual skew cyclic code over R if and only if C1,C2and C3are self-dual skew cyclic codes of length n over Fq.
Proof(1)In light of Theorem 2.5,we obtain
(2)C is a self-dual skew cyclic code over R if and only if g(x)=(x),i.e.,g1(x)=(x),g2(x)=(x)and g3(x)=(x).Thus C is a self-dual skew cyclic code over R if and only if C1,C2and C3are self-dual skew cyclic codes of length n over Fq.
Example 1Let ω a primitive element of F9(where ω =2ω +1)and Θ be the Frobenius automorphism over F9,i.e.,Θ(a)=a3for any a∈F9.Then
Let g1(x)=2+(2+ ω)x+(1+2ω)x3+x4and g2(x)=g3(x)=2+x+(2+2ω)x2+x3.Then C1= 〈g1(x)〉and C2=C3= 〈g2(x)〉are skew cyclic codes of length 6 over F9with dimensions k1=2,k2=k3=3,respectively.Take g(x)=e1g1(x)+e2g2(x)+e3g3(x),then C is a skew cyclic code of length 6 over R.Thus the Gray image of C is a[18,8,4]code over F9.
4 LCD Codes over R
Linear complementary dual codes(which is abbreviated to LCD codes)are linear codes that meet their dual trivially.These codes were introduced by Massey in[12]and showed that asymptotically good LCD codes exist,and provide an optimum linear coding solution for the two-user binary adder channel.In[13],Sendrier indicated that linear codes with complementary-duals meet the asymptotic Gilbert-Varshamov bound.They are also used in counter measure to passive and active side channel analyses on embedded cryto-systems(see[14]).In recent,we in[15]investigated LCD codes finite chain ring.Motivated by these works,we will consider the LCD codes over R.
Suppose that f(x)is a monic(i.e.,leading coefficient 1)polynomial of degree k with f(0)=c0.Then by monic reciprocal polynomial of f(x)we mean the polynomial(x)=c−1f∗(x).
We recall a result about LCD codes which can be found in[16].
Proposition 4.1If g1(x)is the generator polynomial of a cyclic code C of length n over Fq,then C is an LCD code if and only if g1(x)is self-reciprocal(i.e.,(x)=g1(x))and all the monic irreducible factors of g1(x)have the same multiplicity in g1(x)and in xn−1.
Theorem 4.2If C=e1C1⊕e2C2⊕e3C3is a linear code over R,then C is a LCD code over R if and only if C1,C2and C3are LCD codes over Fq.
ProofC is a LCD code over R if and only if C∩C⊥={0}.By Theorem 2.5,we know that C∩C⊥={0}if and only if C1∩C⊥1={0},C2∩C⊥2={0},and C3∩C⊥3={0},i.e.,C1,C2and C3are LCD codes over Fq.
By means of Proposition 4.1 and above theorem,we have the following corollary.
Corollary 4.3Let C=e1C1⊕e2C2⊕e3C3is a cyclic code of length n over R,and let C1= 〈g1(x)〉,C2= 〈g2(x)〉and C3= 〈g3(x)〉be cyclic codes of length n over Fq.Then C is a LCD code over R if and only if gi(x)is self-reciprocal(i.e.,(x)=gi(x))and all the monic irreducible factors of gi(x)have the same multiplicity in gi(x)and in xn−1 for i=1,2,3.
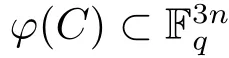
ProofIf x ∈ C ∩ C⊥,then x ∈ C and x ∈ C⊥.It follows that ϕ(x)∈ ϕ(C)and ϕ(x)∈ ϕ(C⊥).Hence ϕ(C ∩C⊥)⊂ ϕ(C)∩ϕ(C⊥).
On the other hand,if ϕ(x)∈ ϕ(C)∩ ϕ(C⊥),then there are y ∈ C and z∈ C⊥such that ϕ(x)= ϕ(y)= ϕ(z).Since ϕ is an injection,x=y=z∈ C ∩C⊥,which implies that
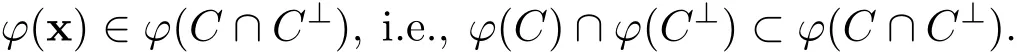
Thus ϕ(C)∩ ϕ(C⊥)= ϕ(C ∩C⊥).
By Theorem 2.3,we ϕ(C ∩C⊥)= ϕ(C)∩ϕ(C)⊥.It follows that C ⊂ Rnis LCD if and only if the linear code ϕ(C)is LCD.
Example 2x4−1=(x+1)(x+2)(x+w2)(x+w6)in F9.Let g1(x)=g2(x)=g2(x)=x+1.Then C1=C2=C3= 〈g1(x)〉are LCD cyclic codes over F9with parameters[4,3,2],respectively.Suppose that C=e1C1⊕e2C2⊕e3C3is a cyclic code of length n over R.By Theorem 2.6 and Theorem 4.5,ϕ(C)is a LCD code with parameters[12,9,2],which is an optimal code.
References
[1]Hammous A R,Kumar Jr P V,Calderbark A R,Sloame J A,Sol´e P.The Z4-linearity of Kordock,Preparata,Goethals,and releted codes[J].IEEE Trans.Inform.The.,1994,40:301–319.
[2]Zhu S X,Wang Y,Shi M J.Some results on cyclic codes over F2+vF2[J].IEEE Trans.Inform.The.,2010,56(4):1680–1684.
[3]Liu X S,Liu H L.Cyclic codes over F2+uF2+vF2[J].Qhin.Quart.J.Math.2014,29(2):113–126.
[4]Boucher D,Geiselmann W,Ulmer F.Skew cyclic codes[J].Appl.Alg.Eng.Comm.,2007,18(4):379–389.
[5]Abualrub T,Seneviratne P.Skew codes over rings[J].Hong Kong:IMECS,2012,2:846–847.
[6]Gao J.Skew cyclic codes over Fp+vFp[J].J.Appl.Math.Inform.,2013,31:337–342.
[7]Gursoy F.Siap I,Yildiz B.Construction of skew cyclic codes over Fq+vFq[J].Adv.Math.Commun.,2014,8:313–322.
[8]Wood J.Duality for modules over finite rings and applications to coding theory[J].Amer.J.Math.,1999,121:555–575.
[9]Anderson F W,Fuller K R.Rings and categories[M].New York:Springer,1992.
[10]Zhan Y T.Reseasch on constacyclic ocdes over some clsses of finite non-chian ring[D].Hefei:Hefei University of Technology,2013.
[11]Boucher D,Ulmer F.Coding with skew polynomial ring[J].J.Symb.Comput.,2009,44(12):1644–1656.
[12]Massey J L.Linear codes with complementary duals[J].Discrete Math.,1992:106/107:337–342.
[13]Sendrier N.Linear codes with complementary duals meet the Gilbert-Varshamov bound[J].Disc.Math.,2004,304:345–347.
[14]Carlet C,Guilley S.Complementary dual codes for counter-measures to side-channel attacks[J].Adv.Math.Commun.,2016,10(1):131–150.
[15]Liu X S,Liu H L.LCD codes over finite chain rings[J].Finite Field Appl.,2015,15:1–19.
[16]Yang X,Massey J L.The condition for a cyclic code to have a complementary dual[J].Disc.Math.,1994,126:391–393.
