无序反射下分离时间量子行走的纠缠特性研究

安志云,李志坚

(山西大学 理论物理研究所,山西 太原 030006)

0 引言

近些年,在量子行走研究领域,无论是理论研究[1-4]还是实验研究[5-8]都取得了很大的进展。作为经典随机行走的量子力学推广,量子行走是一个简单却应用广泛的模型[9]。例如利用量子行走可以执行量子搜索算法[10],可以模拟诸如光合作用中的能量传输等一些复杂的生物过程[11],可以探索拓扑相并实现人造拓扑绝缘体材料[12]等等。量子行走与经典随机行走的不同之处在于量子态的相干性,这会使得量子行走呈现出传播速度更快,位置方差随时间平方变化的特点,而经典情况下位置方差则随时间线性变化[1]。如果经典系统存在相干性,量子行走的特性也可以通过经典系统来模拟,比如在光学平台上,就是用相干光而不是单光子态来实现量子行走的[13-14]。然而,一个实际系统一般不是完全孤立的,也不是完美无缺的,其无可避免地会和外界环境相互作用,或者或多或少地存在一些缺陷。这些因素会导致系统退相干,改变量子行走的传输行为。鉴于此,研究量子行走受噪声或无序环境的影响是一个非常重要的课题[15-17]。安德森在研究无序介质的电导特性时已经发现,处于静态无序介质中的一个量子粒子,在其演化过程中不能任意远地离开其初始位置[18]。这一被称为安德森局域化的现象在一个粒子进行量子行走时也被观察到[19]。在分离时间量子行走中,这种无序效应可以通过随机改变硬币算符来等效[20-21],也可以通过分立位置空间中不同格点间的连接边漏连所产生[22-23]。前一种情况人们研究的较多,而后一种情况的研究相对较少。目前人们所研究的系统一般为位置空间无限大的开放系统,研究的焦点主要集中在退相干、传输特性以及渐进行为等不同方面[15-16,24-26]。本文中,我们研究具有反射边界的一维有限长格点线上的分离时间量子行走,讨论连接边无序断开对量子行走位置自由度和硬币自由度的纠缠特性的影响。

1 一维有限长格点线上的分离时间量子行走

分离时间量子行走是经典分离时间随机行走的量子力学推广,除了位置空间外,还需要一个硬币空间,由硬币空间中的硬币态来决定在位置空间行走的方向。在经典随机行走中,一个硬币只有正面朝上或反面朝上两种状态,根据硬币的这两种状态,来决定粒子在一维位置空间中是向左走一步还是向右走一步。与此不同的是,量子行走中的硬币在硬币空间中除了处于上述两种正交态外,还可以处于这两种态的任意相干叠加态。分离时间量子行走的位置由格点位置态{|x〉:x∈Ζ}描述,张开位置空间ΘP,正交的硬币态{|c〉:c=↑,↓}张开二维的硬币空间Θc,整个希尔伯特空间是由ΘP和Θc构成的直积空间。这样,量子行走的基矢为|x,c〉=|x〉P⊗|c〉C,其任意时刻的量子态可表示为

(1)

其中Ac(x,t)为t时刻量子行走硬币态为c且位于x处的概率幅。量子行走每一步演化

|ψ(t+1)〉=U|ψ(t)〉,

(2)

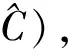
(3)

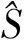
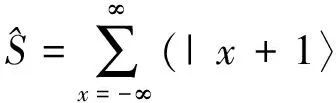
〈x|⊗|↑〉〈↑|+|x-1〉〈x|⊗|↓〉〈↓|).

(4)

(5)

对于空间和时间都均匀的量子行走,Hadamard算符和不同的初态选择可以给出量子行走的所有可能结果[27],其t步演化后的状态|ψ(t)〉可以由方程(3)的t次幂作用于初态|ψ(0)〉得到。

如果量子行走不是在一维无限长格点线上,而是在具有边界的有限长格点线上行走,则量子行走在边界处需要特别定义。其中一种定义是,在右边界处,硬币态为|↑〉的粒子停在边界上不动,硬币态翻转变为|↓〉;在左边界处,硬币态为|↓〉的粒子停在边界上不动,硬币态翻转变为|↑〉,我们把这种定义称为反射边界。相应的条件平移算符变为

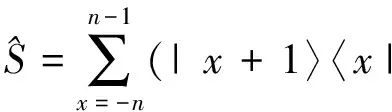
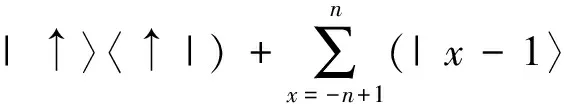
|n〉〈n|⊗|↓〉〈↑|+|-n〉〈-n|⊗|↑〉〈↓|,

(6)

(7)

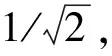
Px=Tr[|x〉〈x|⊗ICUt|ψ(0)〉〈ψ(0)|(U+)t].

(8)

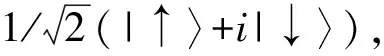
⊗(|↑〉+i|↓〉)],

(9)

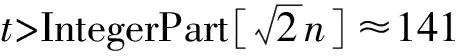
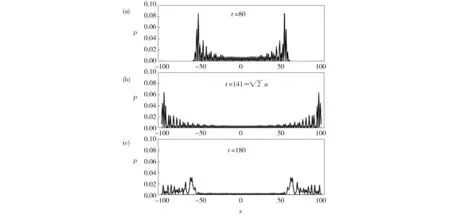
Fig.1 Probability distributions of quantum walk on a lattice segmentwith reflecting boundary are plotted for different time steps图1 反射边界下，一维量子行走在有限长格点线上演化不同步数时的概率分布图

2 一维无序反射分离时间量子行走

在上一节的基础上,我们进一步考虑相邻格点间的连接边随机断开,从而引入无序的情况。我们赋予相邻两格点x和x+1的连接边一个从0到1取值的随机数p(x),如果p(x)小于等于某一临界值p0,则表示格点x和x+1之间的连接边是相连的,否则,如果p(x)大于临界值p0,则表示两格点之间是断开的。p0称为逾渗概率,其大小决定着整条格点线中连接边断开的多少。p0越小,表示断开的边越多。p0=1意味着每条边都是连通的,而p0=0则表示每条边都是断开的。每断开一条连接边,相当于在格点线中多增加了一对边界,此时的条件平移算符可相应地表示为

〈x|⊗|↑〉〈↑|+δf(x),0|x〉〈x|⊗|↓〉〈↑|]+

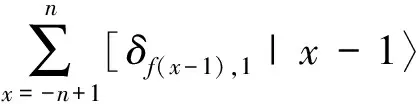
|n〉〈n|⊗|↓〉〈↑|+|-n〉〈-n|⊗|↑〉〈↓|.

(10)

引入随机无序后,有限长格点线上的连接边所对应的随机数在位置空间形成一种分布。因为每个随机数的大小决定着粒子能不能传输,因此可称这一分布为逾渗分布。对于分离时间量子行走,按照逾渗分布在位置和时间上的变化不同,可以把无序分为两种类型。一种是量子行走演化的每一步在位置空间的逾渗分布是相同的,也就是说每一步演化的条件平移算符都是相同的,这样的无序称之为静态无序;另一种是量子行走在演化的每一步都重新选取逾渗分布,每一步演化的条件平移算符不同,则称这样的无序为动态无序。由于静态无序下量子行走的演化算符与时间步无关,演化t步后,其量子态|ψ(t)〉仍可由演化算符U的t次幂作用于初态|ψ(0)〉得到,即|ψ(t)〉=Ut|ψ(0)〉,但对于动态无序下的量子行走,其每一步的演化算符不同,t步后的量子态只能通过|ψ(t)〉=U(t)U(t-1)…U(1)|ψ(0)〉一步一步作用而来。

3 无序反射下分离时间量子行走的纠缠动力学

通过有限长格点线上相邻格点间的连接边随机断开引入无序后,接下来我们主要研究量子行走分别从局域化初态和非局域化初态开始演化,在静态无序和动态无序的影响下,量子行走位置自由度和硬币自由度之间的纠缠随时间的变化。量子纠缠是用来进行量子信息处理和量子计算的重要物理资源,它可以是不同子系统之间的纠缠,也可以是不同自由度之间的纠缠。由于量子纠缠是量子系统特有的性质,在经典系统中没有与之对应的物理量。一般情况下,由于周围环境、噪声以及无序等一些因素的影响,会使量子系统退相干,从而导致纠缠的减小或完全消失。然而,在量子行走中,文献[3]指出通过随机的改变硬币算符引入无序反而会在长时间极限下产生最大纠缠。受此启发,本文中我们通过与之不同的方式引入无序效应,结果也表现出无序增强纠缠的现象。

E=-Tr(ρPlog2ρP)=-Tr(ρClog2ρC).

(11)

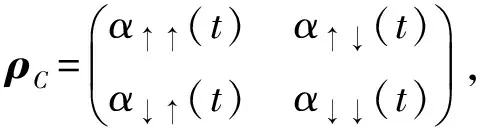
(12)

纠缠熵的取值范围为E(t)∈[0,1],对于最大纠缠态E(t)=1,而对于可分离态E(t)=0。

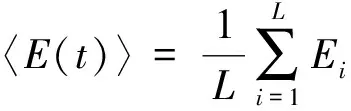
3.1 局域化初态的纠缠动力学

Fig.2 Variations of entanglement with time steps are plotted for different values of percolation probability p0when the quantum walk starting from a local initial state is on the lattice segment with (a) static percolation and (b) dynamical percolation; (c) the entanglement evolution with longer time steps in the case without percolation p0=1图2 选取不同的逾渗概率p0，量子行走从局域初态开始演化时，硬币自由度和位置自由度之间的纠缠随演化步数的变化(a)静态逾渗;(b)动态逾渗；(c)没有逾渗即p0=1时，纠缠演化更长时间的变化图

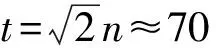
3.2 非局域初态的纠缠动力学

为了研究量子行走的传输性质,一般选取局域初态,由此可以清楚地讨论它在位置空间的扩展性质。然而,在许多量子信息处理中,初态往往是非局域的,如量子搜索的初态就是在位置空间等概率分布的非局域态。下面我们在有限长格点线上选取这种等概率分布的初态,来研究无序及初态对量子行走纠缠动力学的影响。

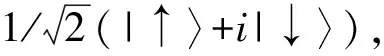
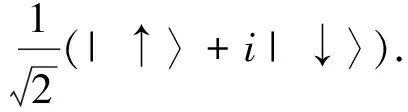
(13)

选取不同的逾渗概率,图3(a)和(b)分别给出静态无序和动态无序下,平均纠缠〈E(t)〉随时间的变化曲线。与图2相比,量子行走的统计平均纠缠动力学发生了很大变化。首先,在没有无序的情况下,量子纠缠大幅变小,而且由于演化一开始边界就对量子行走有反射作用,使得干涉效应在纠缠动力学变化过程中表现得不再明显;其次,在静态无序下,量子行走的纠缠在某一常数值附近的振荡幅度更大,虽然和图2(a)一样,随着逾渗概率的增加,这一常数值也增大,但不同的是这一常数值可以大于没有无序时的纠缠值,表现出静态无序也能增强纠缠的特性;最后,对于动态无序量子行走,两种初态导致的纠缠动力学变化的趋势基本相同,都能在长时间极限下趋向于最大纠缠,只是非局域初态使得纠缠增加的更快。

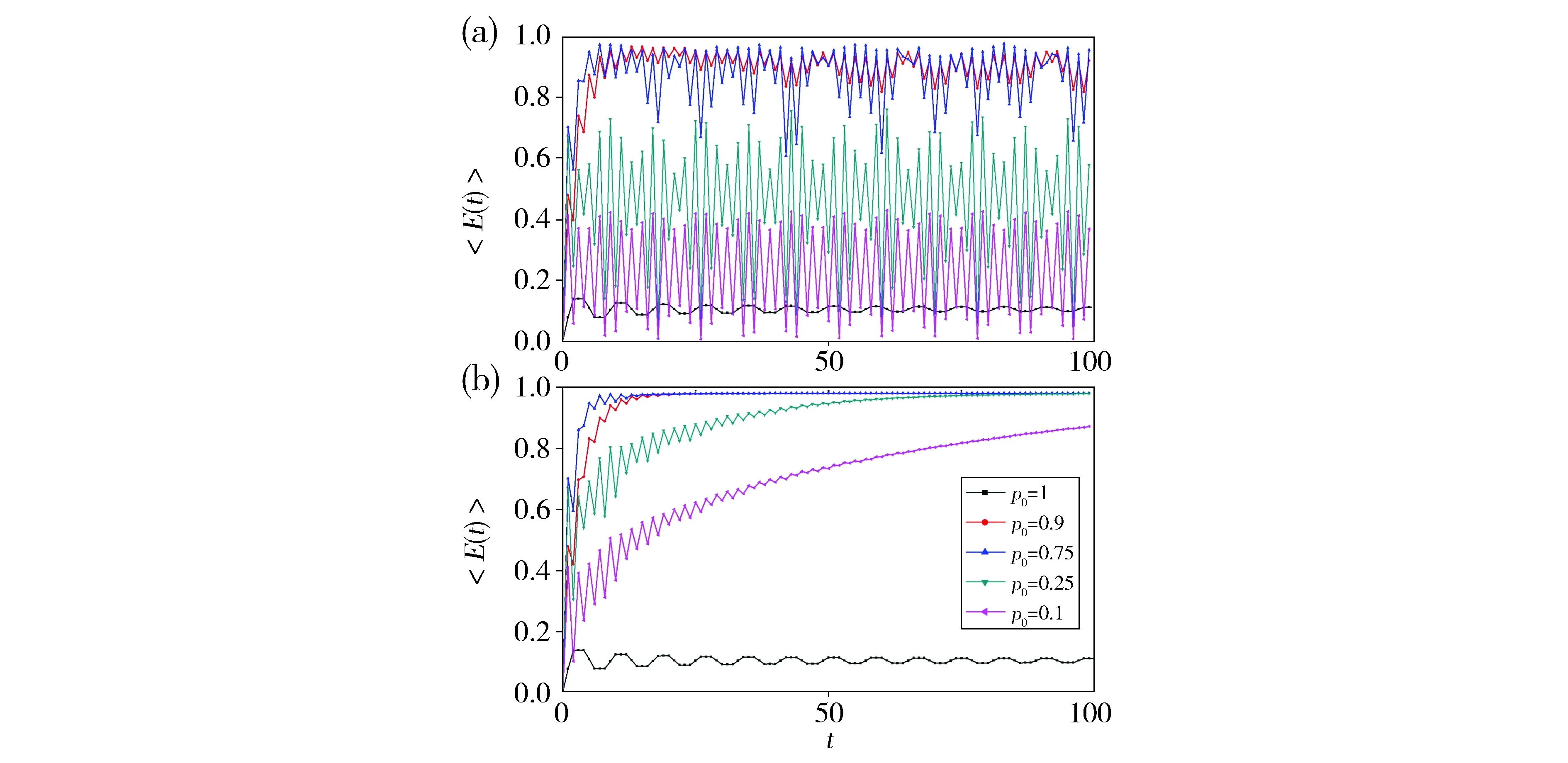
Fig.3 Variations of entanglement with time steps are plotted for different values ofpercolation probability p0 when the quantum walk starting from a non-localinitial state is on the lattice segment with (a) static percolation and (b) dynamical percolation图3 选取不同的逾渗概率p0，量子行走从非局域初态开始演化时，硬币自由度和位置自由度之间的纠缠随演化步数的变化 (a)静态逾渗 (b)动态逾渗

4 结论

本文首先引入具有反射边界的一维有限长格点线上的分离时间量子行走,在边界处粒子(行走者)不能继续行走,但其硬币态却要发生反转,这样定义的条件平移算符仍具有幺正性;接着通过两种方式随机地断开相邻格点间的连接边引入无序效应,一种方式是静态的,量子行走的每一步所断开的连接边分布是相同的,另一种方式是动态的,量子行走的每一步都重新随机断开连接边;最后选取局域和非局域的两种不同初态,研究了静态无序和动态无序对量子行走硬币自由度和位置自由度之间的动力学纠缠的影响。多次计算后的统计平均结果表明,局域初态下,边界反射导致的干涉效应能够在没有无序的动力学纠缠中清楚地显现。引入无序后,每断开一条连接边,相当于增加了一对边界,使得波函数干涉图样越来越无规律,从而反射边界产生的效应被覆盖。这种情况下,只有动态无序能够使得纠缠在某时刻大于没有无序时的纠缠值,表现出纠缠增强,而对于静态无序则不会出现纠缠增强的结果。当初态为非局域态时,没有无序时的纠缠值大幅减小,致使静态无序和动态无序都能够增强纠缠。特别是,无论哪种初态,动态无序都能够在无穷长时间极限下产生最大纠缠,而且这一特性与无序强度没有关系。

参考文献：

[1] Kempe J.Quantum Random Walks:An Introductory Overview[J].ContempPhys,2003,44:307-327.DOI:10.1080/00107151031000110776.

[2] Venegas-Andraca S E.Quantum Walks:A Comprehensive Review[J].QuantumInfProcess,2012,11:1015-1106.DOI:10.1007/s11128-012-0432-5.

[3] Vieira R,Amorim E P M,Rigolin G.Dynamically Disordered Quantum Walk as a Maximal Entanglement Generator[J].PhysRevLett,2013,111:180503-13.DOI:10.1103/PhysRevLett.111.180503.

[4] Beggi A,Buscemi F,Bordone P.Quantum Correlations of Identical Particles Subject to Classical Environmental Noise[J].QuantumInfProcess,2016,15:3711-3743.DOI:10.1007/s11128-016-1334-8.

[5] Karski M,Förster L,Choi J M,etal.Quantum Walk in Position Space with Single Optically Trapped Atoms[J].Science,2009,325:174-177.DOI:10.1126/science.1174436.

[6] Broome M A,Fedrizzi A,Lanyon B P,etal.Discrete Single-photon Quantum Walks with Tunable Decoherence[J].PhysRevLett,2010,104:153602.DOI:10.1103/PhysRevLett.104.153602.

[7] Jeong Y C,Di Franco C,Lim H T,etal.Experimental Realization of a Delayed-choice Quantum Walk[J].NatCommun,2013,4:2471-7.DOI:10.1038/ncomms3471.

[8] Preiss P M,Ma R,Tai M E,et al.Strongly Correlated Quantum Walks in Optical Lattices[J].Science,2015,347:1229-1233.DOI:10.1126/science.1260364.

[9] Aharonov Y,Davidovich L,Zagury N.Quantum Random Walks[J].PhysRevA,1993,48(2):1687-1690.293.DOI:10.1007/s40509-016-0078-6.

[10] Shenvi N,Kempe J,Whaley K B.Quantum Random-walk Search Algorithm[J].PhysRevA,2003,67(5):052307-11.DOI:10.1103/PhysRevA.67.052307.

[11] Mohseni M,Rebentrost P,Lloyd S,etal.Environment-assisted Quantum Walks in Photosynthetic Energy Transfer[J].JChemPhys,2008,129(17):174106-9.DOI:10.1063/1.3002335.

[12] Kitagawa T,Rudner M S,Berg E,etal.Exploring Topological Phases with Quantum Walks[J].PhysRevA,2010,82(3):21504-21510.DOI:10.1103/PhysRevA.82.033429.

[13] Rohde P P,Schreiber A,Jex I,etal.Multi-walker Discrete Time Quantum Walks on Arbitrary Graphs,Their Properties and Their Photonic Implementation[J].NewJPhys,2010,13:013001-9.DOI:10.1088/1367-2630/13/1/013001.

[14] Jeong H,Paternostro M,Kim M S.Simulation of Quantum Random Walks using the Interference of a Classical Field[J].PhysRevA,2004,69:012310-7.DOI:10.1103/PhysRevA.69.012310.

[15] Romanelli A,Siri R,Abal G,etal.Decoherence in the Quantum Walk on the Line[J].PhysA,2005,347:137-152.DOI:10.1016/j.physa.2004.08.070.

[16] Leung G,Knott P,Bailey J,etal.Coined Quantum Walks on Percolation Graphs[J].NewJPhys,2010,12:123018-25.DOI:10.1088/1367-2630/12/12/123018.

[17] Li Z J,Wang J B.Single-point Position and Transition Defects in Continuous Time Quantum Walks[Z/OL].SciRep,2015,5:13585-11.DOI:10.1038/srep13585.

[18] Anderson P W.Absence of Diffusion in Certain Random Lattices[J].PhysRev,1958,109(5):1492-1505.DOI:10.1103/PhysRev.109.1492.

[19] Römer R A,Schreiber M.No Enhancement of the Localization Length for Two Interacting Particles in a Random Potential[J].PhysRevLett,1997,78(3):515-518.DOI:10.1103/PhysRevLett.78.515.

[20] Vieira R,Amorim E P M,Rigolin G.Entangling Power of Disordered Quantum Walks[J].Physics,2014,89(4):042307-12.DOI:10.1103/PhysRevA.89.042307.

[21] Zeng M,Yong E H.Discrete-Time Quantum Walk with Phase Disorder:Localization and Entanglement Entropy[J].SciRep,2017,7:12024.DOI:10.1038/s41598-017-12077-0.

[22] Rigovacca L,Di Franco C.Two-walker Discrete-time Quantum Walks on the Line with Percolation[J].SciRep,2016,6：22052.DOI:10.1038/srep22052.

[23] An Z Y,Li Z J.Properties of Distribution and Entanglement in Discrete-Time Quantum Walk with Percolation[J].ActaPhysicsSinica,2017,66:130303.DOI:10.7498/aps.66.130303.

[24] Schreiber A,Cassemiro K N,Potocˇek V,etal.Decoherence and Disorder in Quantum Walks:From Ballistic Spread to Localization[J].PhysRevLett,2011,106:180403-5.DOI: 10.1103/PhysRevLett.106.180403.

[26] Vakulchyk I，Fistul M V,Qin P,etal,Anderson Localization in Generalized Discrete-Time Quantum Walks[J].PhysRevB,2017,96:144204.DOI:10.1103/PhysRevB.96.144204.

[27] Tregenna B,Flanagan W,Maile R,etal.Controlling Discrete Quantum Walks:Coins and Initial States[J].NewJPhys,2003,5:83-11.DOI:10.1088/1367-2630/5/1/383.