免疫集体噪声的量子密钥协商协议

何业锋

西安邮电大学 通信与信息工程学院，西安 710121

1 引言

自从第一个量子密钥分发（Quantum Key Distribution，QKD）协议（即BB84协议[1]）提出后，量子密码得到了快速发展[1-4]，各种量子密码协议[3-6]被提出来。量子密钥协商[7-8]（Quantum Key Agreement，QKA）是其中非常重要的一种，它能实现通信双方或多方利用公开量子信道建立一个共享密钥，并且所有参与方对密钥的影响是相同的。任何参与方或子团体不能单独决定共享密钥，即协议要能抵抗参与者攻击。与“一次一密”结合可以实现无条件安全的保密通信。因此，这类协议的设计有重要的理论和实际意义。

周等人[7]利用量子隐形传态技术提出了第一个QKA协议。然而它不能抵抗参与者攻击[9]。随后，Hsueh等人[8]提出了一个不能抵抗CNOT攻击[10]的QKA协议。基于BB84协议[1]和延迟测量技术，Chong等人[11]提出了一个安全且具有较高量子比特效率的两方QKA协议。基于Bell态、四粒子纠缠态和五粒子纠缠态等，一些新的两方或多方QKA协议也相继被提出了[12-24]。随后，Shi和Chong[13]将两方QKA协议的概念推广到了多方QKA（MQKA）协议，并且提出了一个MQKA协议。许多MQKA协议和它们的安全性分析也被相继给出了[17-20]。目前许多QKA协议是工作在理想环境下的。然而在实际量子通信中，噪声是不可避免的，攻击者能利用噪声隐藏其攻击。因此设计QKA协议必须考虑噪声的影响。根据文献[25]知，人们可以将信道噪声建模为集体噪声。而无消相干子空间（Decoherence-Free Subspace，DFS）[25]是消除集体噪声影响的一个有效方法，因为无消相干态（DF态，又称逻辑量子态）几乎不受集体噪声的影响。2014年，Huang等人[15]利用逻辑量子态给出了一个两方QKA协议在噪声信道上的实现。随后，Huang等人[26]又利用逻辑量子态设计了免疫集体噪声的两方QKA协议。由于用逻辑量子态设计QKA协议明显降低了协议的量子比特效率。因此，这几个免疫集体噪声的QKA协议都有较低的量子比特效率。He等人[27]利用五粒子逻辑量子态提出了两个免疫集体噪声的QKA协议，协议有较高的量子比特效率。然而，这两个协议的量子态准备过程和协议执行过程都比较复杂。因此，设计简单且具有高量子比特效率的免疫集体噪声的QKA协议是非常有意义的。

在本文中，基于逻辑Bell态设计了两个分别免疫集体退相位噪声和集体旋转噪声的两方QKA协议。协议双方利用幺正变换和延迟测量技术能公平地建立一个共享密钥。通过在Bob实验室里安装波长量子滤波器（wavelength quantum filter）和光子数分离器（Photon Number Splitter，PNS）来抵抗特洛伊木马攻击[28-30]。并且诱骗逻辑量子比特的使用确保了协议面对其他攻击时的安全性。效率分析和比较表明新协议不但具有较高的量子比特效率，而且其量子态准备过程和协议执行过程都比较简单。

2 预备知识

2.1 量子纠缠态和幺正变换

众所周知，{0,1}形成了Z基，{+,-}形成了X基，其中Bell态为它们形成了四维Hilbert空间的一组完全正交基，即Bell基。四个常用的幺正变换为

2.2 集体噪声与逻辑量子态

在一个集体退相位噪声信道上，两个极化光子0和1受噪声的影响可以表述为[25]：eiφ1，其中φ是随时间变化的集体退相位噪声参数。两个逻辑量子比特以及它们的叠加态都不受集体退相位噪声的影响[25]。而集体旋转噪声对两个极化光子的影响可以表述为：，其中θ是随时间变化的集体旋转噪声参数。两个逻辑量子比特以及它们的叠加都不受集体旋转噪声的影响。

3 免疫集体噪声的两方量子密钥协商协议

通信双方Alice和Bob如果想建立一个共享密钥，则先随机选择各自的保密密钥

3.1 免疫集体退相位噪声的量子密钥协商协议

协议步骤如下：

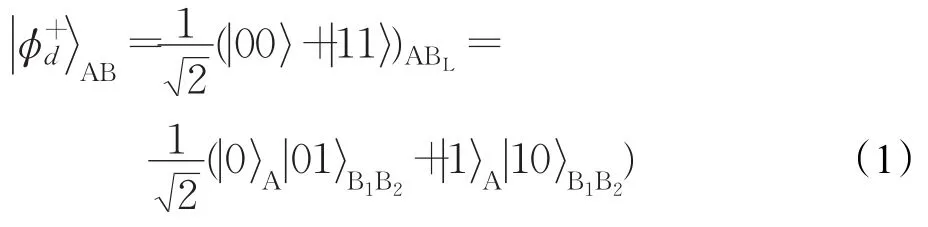
然后，将这n个逻辑Bell态分成两个序列SA和SB。序列SA包含了所有粒子A，序列SB包含所有逻辑量子比特BL（即所有物理量子比特B1和B2）。Alice将m个诱骗逻辑量子比特随机插入序列SB得到随机序列，其中诱骗逻辑量子比特随机取自于集合Alice保留序列 SA，并将序列 S′B发送给Bob。

（2）Bob在他的实验室里安装波长量子滤波器和光子数分离器。Bob收到的所有光子脉冲应当首先通过他的滤波器过滤掉可能出现的不可见光子。当确认Bob收到序列后，Alice公布诱骗逻辑量子比特的位置。Bob随机选出一部分诱骗逻辑量子比特的光子脉冲，利用光子数分离器判断是否存在多光子信号。如果多光子信号的比率高得不合理，则认为存在攻击者的延迟光子。双方终止协议，从协议的第（1）步重新开始。否则，Alice公布诱骗逻辑量子比特的测量基Bob用正确的测量基去测量相应的诱骗逻辑量子比特。Alice公布诱骗逻辑量子比特的初始态。根据测量结果和Alice公布的初始态，Bob计算错误率。若错误率比规定的限门值低，则通信双方执行协议的下一个步骤。否则停止此协议并重新开始。

（3）Alice和Bob协商四个幺正变换Ui1i2：U00=I⊗I，U01=Z⊗I，U10=X⊗X ，U11=X⊗iY 。Bob根据密钥KB，对序列SB中的第i个逻辑量子比特执行幺正变换Ui1i2，其中i1i2=K(i=1,2,…,n)。当执行上述四个幺正变换后，逻辑Bell态AB将变为下面四个GHZ态之一：

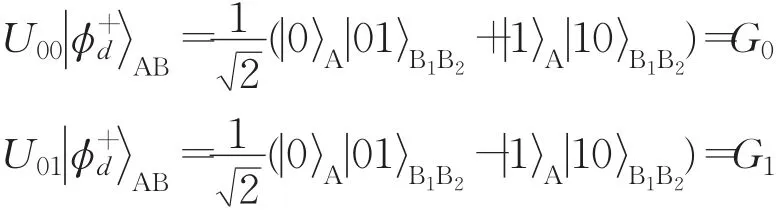
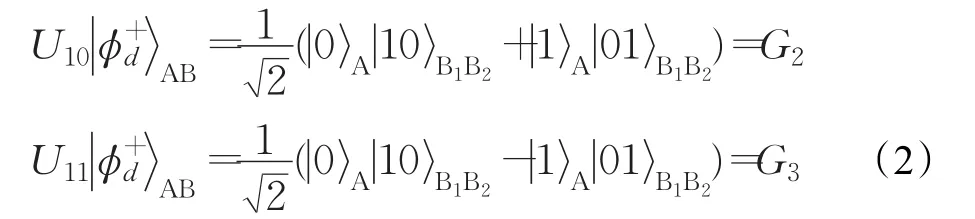
序列SB变为。随后，Bob用置换运算∏n将变为随机序列。然后，他从集合中随机选出m个诱骗逻辑量子比特，并随机插入序列。最后将这个新序列发送给Alice。

（4）当Alice收到后，双方执行与第一次完全相同的窃听检测。同样根据错误率与限门值的关系，来确定继续下一步骤还是重新开始协议。

（5）Alice公布她的密钥KA。根据密钥KA和KB，Bob计算双方的共享密钥：

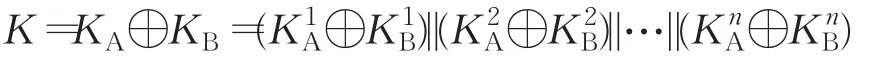
（6）Bob公开宣布置换运算∏n。Alice将其逆置换作用于序列恢复序列。随后，Alice对序列SA和中符号相同的三个粒子依次执行GHZ态测量。根据测量结果和等式（2），Alice计算出KB。因此，她能得到共享密钥：K=KA⊕KB。

柳红跑出一垄地远，突然刹住了脚步，她感觉不对啊，好像有哪儿不对劲儿；烂眼阿根没有动静啊，而且他那个眼神……那个眼神，好像是……柳红折身跑回去，仔细一瞧，不好！烂眼阿根像是……不，应该是……死了。

3.2 免疫集体旋转噪声的量子密钥协商协议

协议步骤如下：

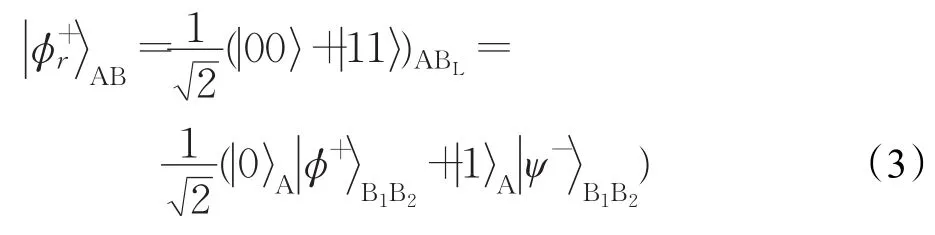
（1）Alice准备n 个逻辑Bell态并且所有粒子A形成了序列SA，所有逻辑量子比特BL形成了序列SB。Alice从集合机选取m个诱骗逻辑量子比特，将其随机插入SB得到序列。Alice保留序列SA，并将发送给Bob。

（2）Bob在他的实验室里安装波长量子滤波器和光子数分离器，来防止两种特洛伊木马攻击。当确认Bob收到序列后，双方执行窃听第一次窃听检测。此窃听检测与第一个协议的窃听检测完全类似。根据错误率与限门值的关系，来确定继续下一步骤还是重新开始协议。

（3）双方首先协商四个幺正变换Ui1i2：U00=I⊗I，U01=Z⊗Z,U10=Z⊗X，U11=iY⊗I。令i1i2=，Bob对序列SB中的第i个逻辑量子比特执行幺正变换Ui1i2(i=1,2,…,n)。执行上述变换后，逻辑Bell态将变化如下：

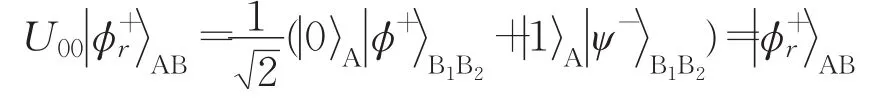
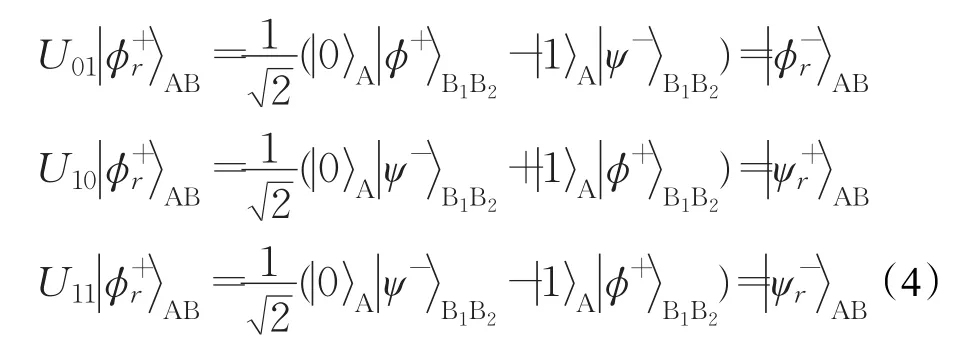
序列SB变为新序列。Bob同样利用置换运算∏n将序列变为一个随机化的序列。类似于协议第一步，他将m个随机的诱骗逻辑量子比特随机插入序列。最后将新序列发送给Alice。

（4）当Alice收到序列后，双方执行与第一次完全相同的窃听检测。

（5）Alice公布密钥KA。同样，Bob计算共享密钥：K=KA⊕KB。

（6）Bob公开宣布置换运算∏n。Alice将逆置换作用于序列恢复序列，并组合序列SA和得到n个逻辑Bell态。根据等式（4）知，它们分别属于四个逻辑Bell态之一。Alice对这n个逻辑Bell态分别执行操作S1=S⊗S⊗S和H1=H⊗H⊗H，其中H是Hadamard门，S是π/2相位门。H能将量子比特和转化为量子比特，而相位门S能将量子比特的相位改变π/2。当执行上述两个变换后，四个逻辑Bell态分别变成四个GHZ态：

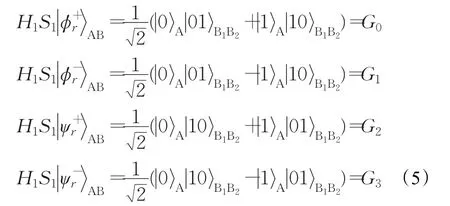
Alice对它们执行三粒子的GHZ态测量。根据测量结果和等式（4）与（5），Alice能计算出 KB和共享密钥：K=KA⊕KB。

4 安全性分析

在本章中，通过安全性分析，证明了这两个QKA协议能抵抗已有攻击。

4.1 参与者攻击

本文的两个QKA协议都用到了延迟测量技术[31]。通过分析知，仅当Alice公开密钥KA后，Bob才告知其置换运算∏n，即Alice才获知序列。故Alice无法通过KB的信息来改变KA的值。同样Bob在获知KA前，就已经将包含KB信息的量子比特发送给了Alice，故他也无法改变KB的值。所以，Alice和Bob都不能独自决定这个共享密钥，即他们都无法成功执行参与者攻击。

4.2 外部攻击

对于QKA协议来说，目前主要的外部攻击方法有：测量-重发攻击、截获-重发攻击、纠缠-测量攻击和特洛伊木马攻击。为了便于说明，下面假设Eve是一个想窃取共享密钥的外部攻击者。

截获-重发攻击和测量-重发攻击：在所有传输的粒子序列中都随机插入了诱骗逻辑量子比特，并且这些诱骗逻辑量子比特随机取自于两个非正交基因此，在窃听检测前，Eve不知道诱骗逻辑量子比特的位置和相应的量子态。如果Eve执行截获-重发攻击，她伪造的序列是随机的，将无法通过窃听检测。同样Eve的测量-重发攻击将会影响诱骗逻辑量子比特的状态。如果假设检测一种攻击的诱骗粒子数量为m，则通信双方能以1-(1/2)m的概率检测到截获-重发攻击，而以1-(3/4)m的概率[32]检测到测量-重发攻击。

纠缠-测量攻击：Eve可以用辅助粒子去纠缠传输的逻辑量子比特来执行纠缠-测量攻击。将这种纠缠变换记为U，用来表示极化态。显然，这些纠缠操作U也会被执行到诱骗逻辑量子比特上。以集体退相位噪声信道为例，这些诱骗逻辑量子比特变化如下：

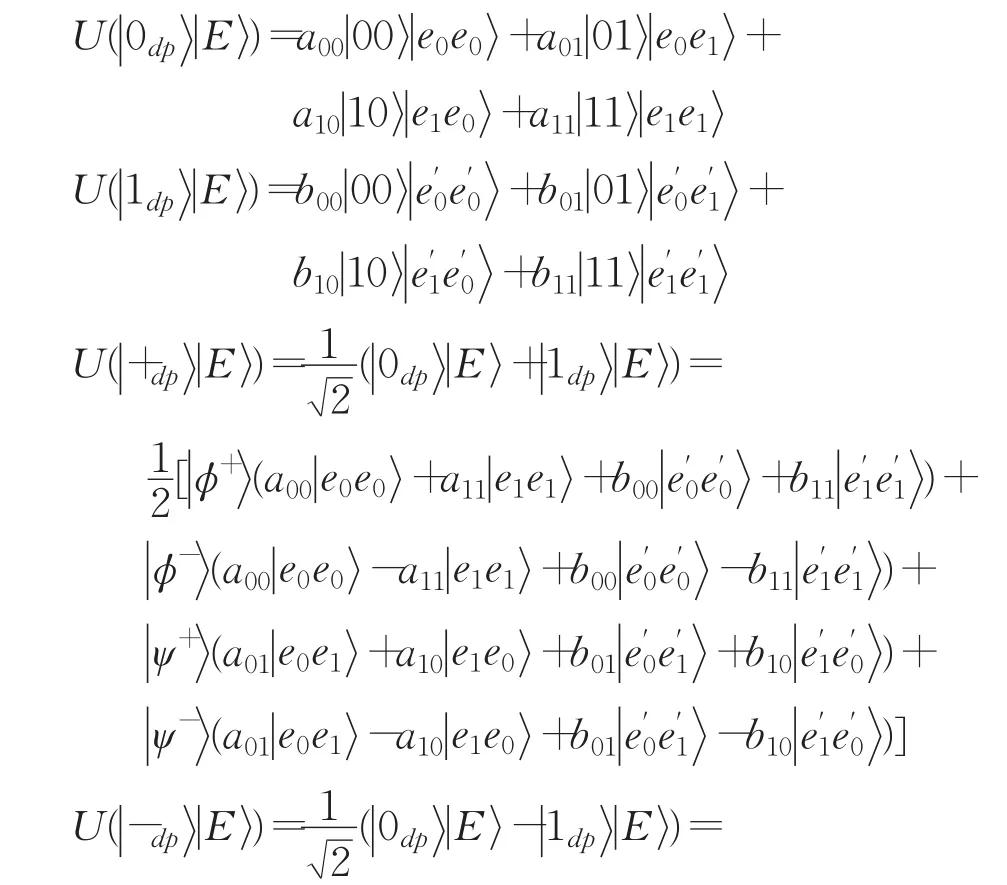
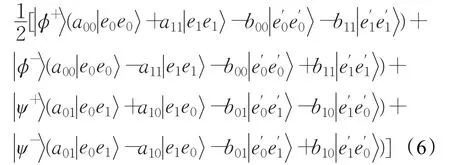
其中如果Eve想在两次窃听检测中不引入错误，Eve的幺正变换U必须满足条件因此，Eve不能区分辅助光子，即Eve不能通过观察辅助光子获取密钥KB的有用信息。否则，攻击将改变诱骗逻辑量子比特的状态，因此无法通过窃听检测。因此，Eve的纠缠-测量攻击失败了。

特洛伊木马攻击：在本文的两个QKA协议中，每个光子在量子信道中被传输两次，因此Eve可能想执行不可见光子窃听（IPE）木马攻击[28]和延迟光子木马攻击[29-30]。然而，Bob在他的实验室里安装了波长量子滤波器和光子数分离器，其中波长量子滤波器能过滤掉不可见光子，而光子数分离器能检测出延迟光子。因此，Eve无法成功执行两种特洛伊木马攻击。

5 效率分析

目前QKA协议的量子比特效率[33]定义为：η=c/(q+b)，其中c指建立共享密钥的比特数量，q指所用量子比特数量，b指用来解码的经典比特数量。由于两个QKA协议都用了n个逻辑Bell态，并且每个传输的量子序列中插入了m个诱骗逻辑量子比特，因此协议中用到的物理量子比特的数量共计q=3n+4m比特。两个协议中解码所需的经典比特数量b=n+2n，通信双方建立共享密钥的比特数量为c=2n比特。所以这两个QKA协议的量子比特效率均为：η=2n/(6n+4m)。由于文献[14，21-22]中一般取m=n的情况对QKA协议的效率进行比较。当m=n时，有η=1/5=20%。文中的两个QKA协议与现有免疫集体噪声的QKA协议的比较如表1所示。通过数据比较知两个协议与文献[27]中的两个QKA协议的量子比特效率相同，都是比较高的。然而，QKA协议的逻辑量子态的准备过程和协议的执行过程都比HM密钥协商协议[27]简单得多。

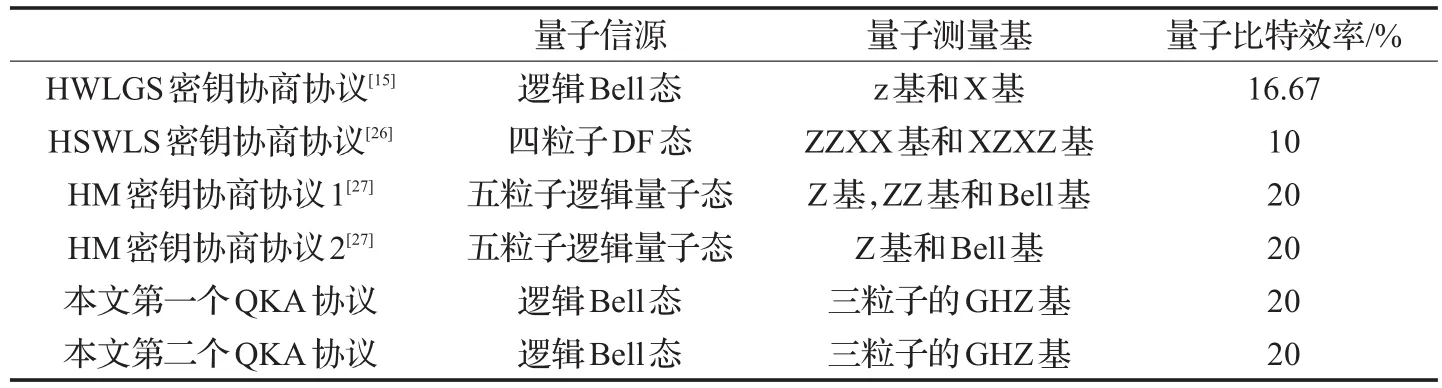
表1 本文QKA协议和现有免疫集体噪声的QKA协议比较

6 结束语

在本文中，基于逻辑Bell态提出了两个分别免疫集体退相位噪声和集体旋转噪声的两方QKA协议。通过对诱骗逻辑量子比特和窃听检测过程的分析，证明了这两个协议是安全的。与已有的几个免疫集体噪声的QKA协议一样，都能抵抗参与者攻击和相关外部攻击，因此，新的免疫集体噪声的QKA协议与已有的免疫集体噪声的QKA协议在安全性上是相当的。通过对新协议的效率分析知，协议量子比特效率较高，虽然它们与HM密钥协商协议有相同的量子比特效率，但协议实现更简单。

：

[1]Bennett C H，Brassard G.Quantum cryptography：publickey distribution and coin tossing[C]//Proceedings of IEEE International Conference on Computers，Systems and Signal Processing.Bangalore：IEEE Press，1984：175-179.

[2]Xu G B，Zhang K J.A novel quantum group signature scheme without using entangled states[J].Quantum Information Processing，2015，14（7）：2577-2587.

[3]Wang L L，Ma W P.Controlled quantum secure communication protocol with single photons in both polarization and spatial-mode degrees of freedom[J].Modern Physics Letters B，2016，30（5）：1650051.

[4]Liu F，Su Q，Wen Q Y.Eavesdropping on multiparty quantum secret sharing scheme based on the phase shift operations[J].International Journal of Theoretical Physics，2014，53（5）：1730-1737.

[5]ElAllati A，ElBaz M，Hassouni Y.Quantum key distribution via tripartite coherentstates[J].Quantum Information Processing，2011，10（5）：589-602.

[6]Yin X R，Ma W P，Liu W Y，et al.Efficient bidirectional quantum secure communication with two-photon entanglement[J].Quantum Information Processing，2013，12（9）：3903-3102.

[7]Zhou N，Zeng G，Xiong J.Quantum key agreement protocol[J].Electronics Letter，2004，40（18）：1149-1150.

[8]Hsueh C C，Chen C Y.Quantum key agreement protocol with maximally entangled states[C]//Proceedings of the 14th Information Security Conference（ISC 2004）.Taipei：National Taiwan University of Science and Technology，2004：236-242.

[9]Tsai C W，Hwang T.On quantum key agreement protocol：CS-I-E[R].Taiwan，China：National Cheng Kung University，2009.

[10]Tsai C W，Chong S K，Hwang T.Comment on quantum key agreement protocol with maximally entangled states[C]//Proceedings of the 20th Cryptology and Information Security Conference（CISC 2010）.Hsinchu：National Chiao Tung University，2010：210-213.

[11]Chong S K，Hwang T.Quantum key agreement protocol based on BB84[J].Optics Communications，2010，283（6）：1192-1195.

[12]Chong S K，Tsai C W，Hwang T.Improvement on quantum key agreement protocol with maximally entangled states[J].International Journal of Theoretical Physics，2011，50（6）：1793-1802.

[13]Shi R H，Zhong H.Multi-party quantum key agreement with Bell states and Bell measurements[J].Quantum Information Processing，2013，12（2）：921-932.

[14]Shukla C，Alam N，Pathak A.Protocols of quantum key agreement solely using Bell states and Bell measurement[J].Quantum Information Processing，2014，13（11）：2391-2405.

[15]Huang W，Wen Q Y，Liu B，et al.Quantum key agreement with EPR pairs and single particle measurements[J].Quantum Information Processing，2014，13（3）：649-663.

[16]申冬苏，马文平，尹逊汝，等.两方量子密钥协商协议的改进[J].西安电子科技大学学报，2015，42（1）：86-90.

[17]Yin X R，Ma W P，Liu W Y.Three-party quantum key agreementwithtwo-photon entanglement[J].International Journal of Theoretical Physics，2013，52（11）：3915-3921.

[18]Xu G B，Wen Q Y，Gao F，et al.Novel multiparty quantum key agreement protocol with GHZ states[J].Quantum Information Processing，2014，13（12）：2587-2594.

[19]Huang W，Wen Q Y，Liu B，et al.Cryptanalysis of a multi-party quantum key agreement protocol with single particles[J].Quantum Information Processing，2014，13（7）：1651-1657.

[20]Zhu Z C，Hu A Q，Fu A M.Improving the security of protocols of quantum key agreement solely using Bell states and Bell measurement[J].Quantum Information Processing，2015，14（11）：4245-4254.

[21]Shen D S，Ma W P，Wang L L.Two-party quantum key agreement with four-qubit cluster states[J].Quantum Information Processing，2014，13（10）：2313-2324.

[22]He Y F，Ma W P.Quantum key agreement protocols with four-qubit cluster states[J].Quantum Information Processing，2015，14（9）：3483-3498.

[23]Sun Z W，Yu J P，Wang P.Efficient multi-party quantum key agreement by cluster states[J].Quantum Information Processing，2016，15（1）：373-384.

[24]He Y F，Ma W P.Two-party quantum key agreement based on four-particle GHZ states[J].International Journal of Quantum Information，2016，14（1）：1650007.

[25]Walton Z D，Abouraddy A F，Sergienko A V，et al.Decoherence-free subspaces in quantum key distribution[J].Physical Review Letters，2003，91（8）：087901.

[26]Huang W，Su Q，Wu X，et al.Quantum key agreement against collective decoherence[J].International Journal of Theoretical Physics，2014，53（9）：2891-2901.

[27]He Y F，Ma W P.Two quantum key agreement protocols immune to collective noise[J].International Journal of Theoretical Physics，2017，56（2）：328-338.

[28]Cai Q Y.Eavesdropping on the two-way quantum communication protocols with invisible photons[J].Physics Letters A，2006，351（1/2）：23-25.

[29]Deng F G，Li X H，Zhou H Y，et al.Improving the security of multiparty quantum secret sharing against Trojan horse attack[J].Physical Review A，2005，72（4）：044302.

[30]Li X H，Deng F G，Zhou H Y.Improving the security of secure direct communication based on the secret transmitting order of particles[J].Physical Review A，2006，74（5）：054302.

[31]Deng F G，Long G L，Wang Y，et al.Increasing the efficiencies of random-choicebased quantum communication protocols with delayed measurement[J].Chinese Physics Letters，2004，21（11）：2097.

[32]Lin J，Hwang T.New circular quantum secret sharing for remote agents[J].Quantum Information Processing，2013，12（1）：685-697.

[33]Cabello A.Quantum key distribution in the Holevo limit[J].Physical Review Letters，2000，85（26）：5635-5638.