基于改进深度孪生网络的分类器及其应用

沈 雁，王 环 ，2，戴瑜兴 ，2

1.湖南大学 电气与信息工程学院，长沙 410082

2.温州大学 数理与电子信息工程学院，浙江 温州 325035

1 引言

在机器学习领域中，大多数的应用问题都是通过分类器模型来解决的。从Rosenblatt研究出感知机（Perceptron）这一线性分类模型以来，对分类器的研究得到了迅速的发展。感知机仅能对线性的数据进行分类，而在现实中许多问题都是非线性的。后向传播算法的出现使得神经网络成功地应用于非线性的分类问题。此时的神经网络还较为简单，通常为三层，即输入层，隐藏层和输出层。Vapnik等人在1992年提出了支持向量机，巧妙地运用核函数方法将非线性问题转换为线性问题。由Hinton和LeCun等进一步发展出来神经网络深度学习算法，使得神经网络的学习能力得到了飞跃式的提高。使得深度学习成为当前机器学习的主流方向。Belzmann机和卷积神经网络等技术的发明，使得深度学习算法在各个领域的应用都超越以往的方法，取得了最好的效果。随着深度学习领域的不断发展，出现了许多优秀的计算框架，例如Caffe，Pytorch，Tensorflow，MXNet等等。其中Pytorch是以Torch为基础，使用Python脚本语言实现的版本。针对于大型的多层神经网络和大规模的训练数据，这些平台都可以使用GPU进行加速，从而极大地缩短训练的时间。

机器学习方法也越来越多地应用于现代生活当中。例如汽车的辅助驾驶系统或者是无人驾驶系统，对道路交通标志的识别都将是其中必不可少的一环。考虑到路况的复杂性，交通标志的识别及分类必须要考虑到各种极端条件，例如夜间暗光，雾霾，标志牌上的污渍等等。因此，分类器必须要有极好的可靠性和鲁棒性。目前已经提出了很多分类器算法。支持向量机（SVM）[1]方法采用非线性核函数映射来解决非线性问题，具有较强的泛化能力，且能很好地处理高维度的数据。但由于其中正比于样本数量的矩阵计算的复杂性，使得其并不适合于具有大规模训练样本的应用。另外，SVM作为二分类算法在解决多分类问题时必须使用多个SVM组合来解决。Adaboost方法则是在训练时，通过T次的迭代训练出T个弱分类器，再采用加权投票形成一个强分类器。其中的弱分类器可以是简单的逻辑回归，SVM，极限学习机（ELM）[2]，以及神经网络。Adaboost方法具有结构简单容易实现，不易于过拟合等优点。但同时，当对Adaboost方法选择越复杂的弱分类器时，则越可能发生过拟合，而像图像类的高维数据通常是需要较复杂的弱分类器的。卷积神经网络[3-6]目前以其超越其分类器的优异性能得到越来越多的应用。常用的卷积神经网络都采用了非常多的网络层来获得较好的效果，如ResNet、AlexNet、VGG和GoogleNet等。这样的网络无论在训练还是使用上都需要相当巨大的计算量。

本文在深度学习的理论基础之上，将用于相似度计算的孪生神经网络构造成分类器。在具有相同结构和共享权值的两组多层神经网络中，分别采用了卷积神经网络层，ReLU，max-pooling以及全连通网络，同时还利用dropout技术来预防过拟合问题。该方法能将在原始图像空间难以划分的图像变换到以基准图像为中心的特征空间，再通过距离的测量达到分类的功能。该孪生神经网络只使用很少的网络层，利用相似度计算来实现一个快速的分类器。针对交通标志识别的应用，将原始数据重新构建为具有正负匹配对的训练集。通过短时间的训练，即可达到非常高的准确率。

2 用于相似度计算的孪生神经网络

2.1 孪生神经网络模型

孪生神经网络构架[7]最早由Bromley和LeCun在1990年为了解决数字签名的校验问题而提出。一个孪生神经网络系统由一对孪生的两个神经网络构成。这两个神经网络之间共享权值和偏置等参数，但输入的是不同的数据。通过神经网络的前向处理，可以将原本在原始空间中分辨困难的数据进行维度规约[8]，从而变得容易分辨。例如48×48的图像块，其原始的维度便是2 304，这样很难对一对图像块进行比较，也就是说很难采用常用的欧式距离计算它们之间的相似度。通过神经网络的处理便可以只提取出其中的特征向量，在孪生神经网络的后端只需对提取的特征向量进行欧式距离计算即可。这是因为在特征空间中，各个图像块的特征向量能反应出它们之间的真实相似度。孪生神经网络的构架见图1。

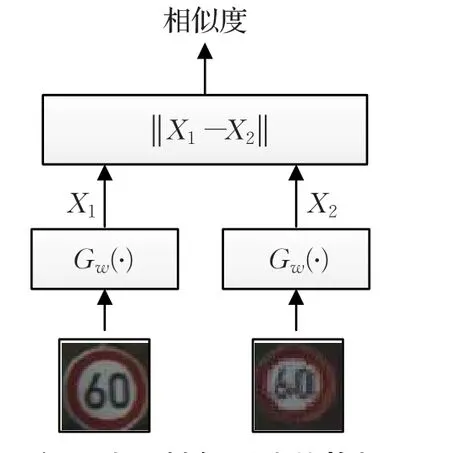
图1 孪生神经网络的构架

为了能够对孪生神经网络进行训练，需要定义可微分的代价函数。因为孪生神经网络的目的不是为了对输入进行分类。因此用于分类的代价函数（例如交叉熵[9]）并不太合适。令X1,X2为孪生神经网络的输入，Y为指示X1和X2是否匹配的二值标签，有Y∈{0,1}。如果X1和X2相似，则Y=0，如果不相似则Y=1。采用的代价函数为如下的形式：

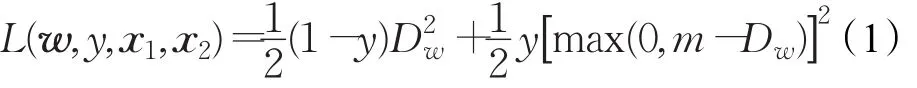
其中Dw为孪生神经网络输出的两个特征向量的欧式距离，即Dw(X1,X2)=||Gw(X1)-Gw(X2)||。由Gw来表示孪生神经网络将输入X1,X2映射到它们的特征向量。m值用于在Gw上定义一个边界，使得只有距离在该范围内的负样本才对损失函数有影响。对于所有的训练样本，最后得到的总体损失函数为：

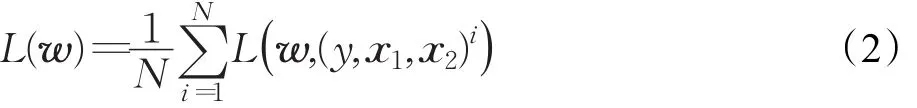
2.2 使用深度网络的实现

本文使用的深度孪生神经网络构架见图2。其分为特征提取网络和相似度计算两个部分。在特征提取网络中，共包含四层的卷积神经网络。不同层次的卷积神经网络用于提取不同层次的特征。以容易理解的第一层卷积神经网络而言，其直接接受输入的图像，并从图像上提取所需的特征。经过训练，其通过都会提取图像中的各式各样的点和边特征。在卷积神经网络的后面使用非线性的Relu激活函数作为该层的神经元。对于大规模的数据来说，ReLu激活函数具有比sigmoid激活函数和tanh激活函数等更好的拟合能力[10]。其也更能增强网络的非线性，以及使得后面的神经网络更具判别性。第三层的卷积网络层产生的结果和第四个卷积网络层的结果会共同输出到全连通神经网络层。因为第四层卷积网络层比第三层卷积网络提取更全局的特征，因此第一个全连通网络接受到的是来自前级多尺度的特征输入，形成多尺度卷积神经网络[11]。另外，在前三个卷积网络层的后面都使用了max-pooling层来提供对微小移动的不变性。每个卷积网络层还使用dropout技术[12]来防止网络的过拟合。第一层全连通网络同时连接到第三层和第四层卷积网络的特征输出，起到承接的作用。第二层的全连通网络的输出为128维的最终特征向量。

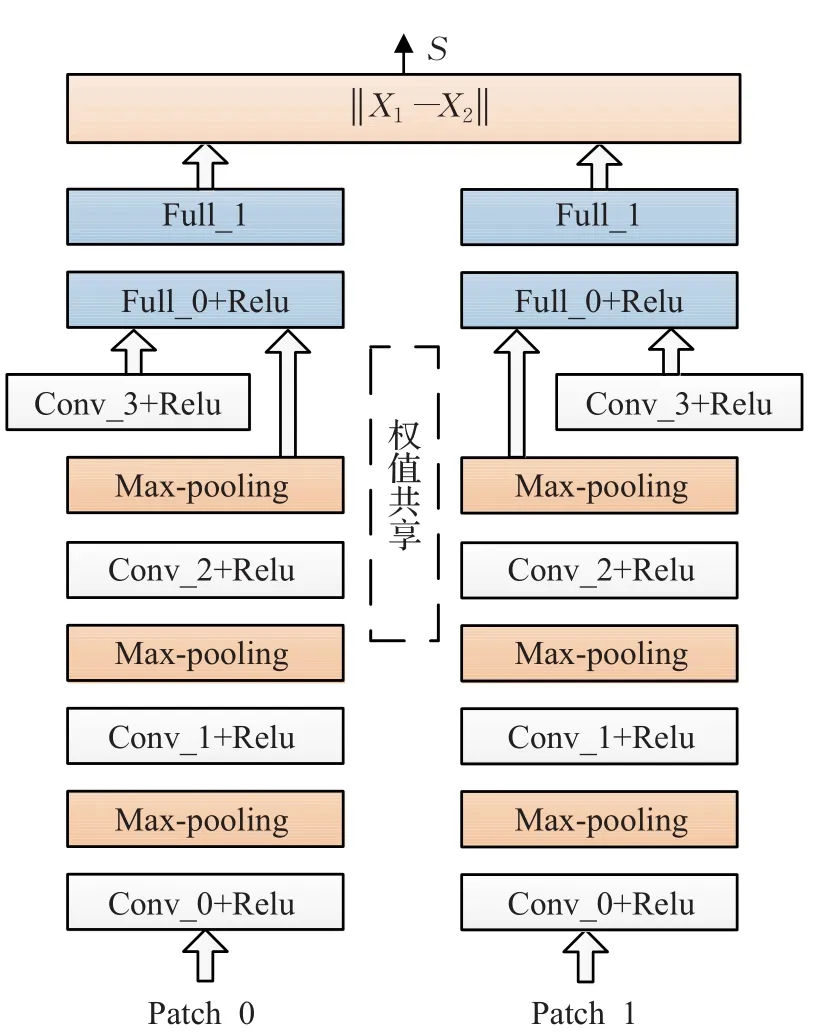
图2 孪生神经网络的结构图

所定义的网络的配置参数见表1。使用的名称中，前缀的“Conv”表示卷积网络层，“Pool”表示max-pooling层，而“Full”则表示全连通网络层。通过插入max-pooling层可以逐步地减少特征的维度，从而减少计算量。

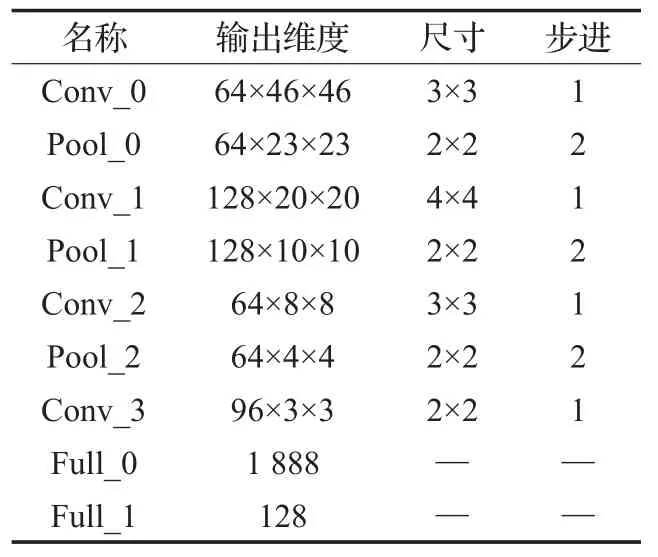
表1 孪生神经网络各个网络层的参数

3 作为分类器的孪生神经网络

前面论述了孪生神经网络作为计算各图像间相似度的一个强有力的工具。据此，便可以将孪生网络进行相应的改装，使之变为非常高效的分类器。首先，为每一个类别在训练样本中选择一个基准样本，并通过大量的正反图像对对孪生网络进行训练。在测试或实际使用中，基准样本和待测样本都会通过孪生网络提取出它们的特征向量。最后通过计算待测样本与各个基准样本的欧式距离，选择具有最高相似度基准样本所对应的类别作为该待测样本的类别。该方法在实现上具有两个优点。其一是只需要使用很少的网络层即可达到良好的效果。在本文中仅使用了4个卷积网络层，4个ReLU层，3个max-pooling层，以及两个全连通网络层。其二是所需的计算量很小。在网络训练完成之后，各类别基准样本的特征向量可以预先进行提取。在对待测样本进行预测时只需要提取其特征向量，然后再计算与各个基准样本的特征向量的距离即可。

识别过程的示意图见图3。为了将孪生神经网络应用为分类器，如何对其进行训练是非常重要的。在一般的采用单一深度网络结构的分类器上，只需要利用给定的分类标签对原始的训练数据集进行训练即可。而如果采用孪生神经网络结构，则需要对原始的训练数据集进行处理，使之符合孪生神经网络的训练模式。首先，需要一个从每个交通标志类的训练样本中确定一个样本作为基准，使得在进行相似度计算时有一个参照（见图4（a））。然后将原始数据集中的样本两两组合成大量的正样本对和负样本对。正样本由基准样本和同类别其他样本形成，负样本由基准样本和不同类别的其他样本形成。具体的孪生神经网络训练集的生成算法为：

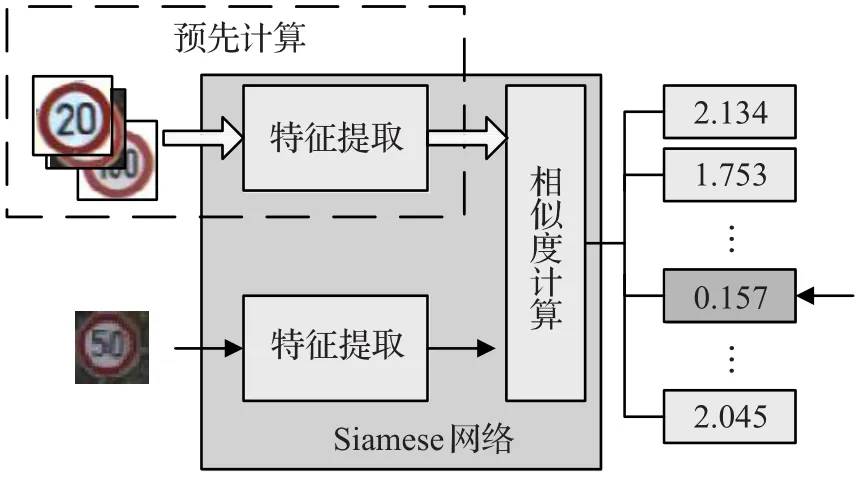
图3 作为分类器使用的孪生网络

图4 （b）生成的8对随机样本

算法1生成正负样本对

forn=0…43do

i=p+

idxs←range(pp+cn)

idxs ← shuffle（idxs）

form=0…cido

Sample.append(i,idxs[m])

l_idxs←range(0,p

r_idxs←range(p+cn,Ns)

idxs←conca（tl_idxs，r_idxs）

idxs← shuffle（idxs）

form=0…cido

Sample.append(i,idxs[m])

return Sample

其中使用了两次随机函数用于随机地挑选不同类别中的某个样本作为负的样本对。同时，为了提高训练的效果，对原始的数据进行扩充是非常重要的。在交通标志识别的应用中，必须考虑到采集的标志图像可能会存在包括位移和旋转等各种变换。为了应对这些不确定的变换，必须在训练中对已有的有限样本尝试进行不同的变换。在实际使用中，可以将图像在x,y坐标上进行相比于图像尺寸±T%的随机位移，±R位的随机旋转，以及相比于图像尺寸进行±S%的缩放。一个包含这些变换的正负样本对见图4（b）。

4 空间变换器网络

4.1 理论分析

理想的模式识别系统的主要特性就是其对目标位置、旋转以及形变的不变性。在CNN中引入的maxpooling层可以用来实现微小的位置不变性。但其对于较大的位置、旋转以及形变等起不到太好的作用。因此空间变换器网络（STN）[13]作为一种有效的解决方案变应运而生。STN可以作为孪生神经网络的前级网络，在无需对输入图像进行标定的情况下，能够自适应地对数据进行空间变换和对齐（包括平移、缩放和旋转等）。因此在原有孪生神经网络上加入空间变换网络，可以进一步地提高匹配的准确性。

STN由三个模块组成，分别为定位网络，网格生成器和采样器，其结构见图5。图中U和V分别为STN的前级网络和后级网络。在本文的应用中，U就是输入的图像块，而V则是孪生网络的其中一组卷积网络。定位网络是一个很小的子网络，同样可以由卷积网络和全连通网络混合组成。该网络通过大量的样本进行自学习来产生一个有利于匹配的变换参数θ，这里的变换可以是简单的位移，旋转或者是常用的仿射变换。对于仿射变换来说，由得到的变换参数组成变换矩阵Tθ，对输入的图像块进行如下的变换：

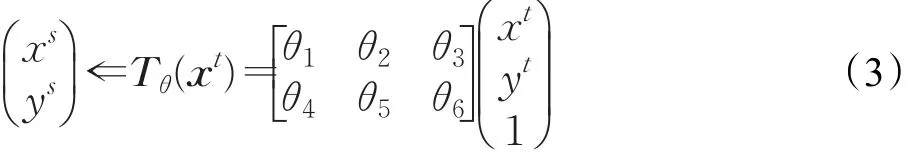
其中θ3和θ6表示平移，θ1和θ5的值的大小表示不同程度的缩放，而 θ1、θ2、θ4和 θ5共同表示对原始图像的旋转。网格生成器的作用是用于计算变换后图像It中每个像素的位置对应到的原始图像中的位置。即给定It中任意一点的坐标xt，通过网格生成器能计算出其对应在原图像Is中的坐标xs。

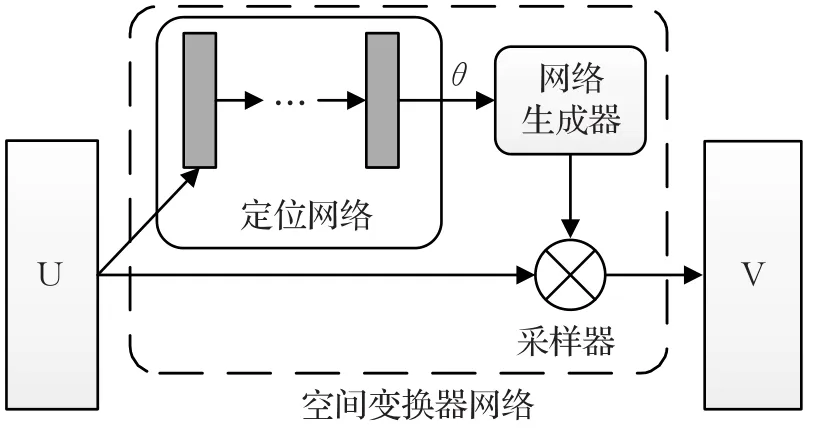
图5 空间变换器网络的结构

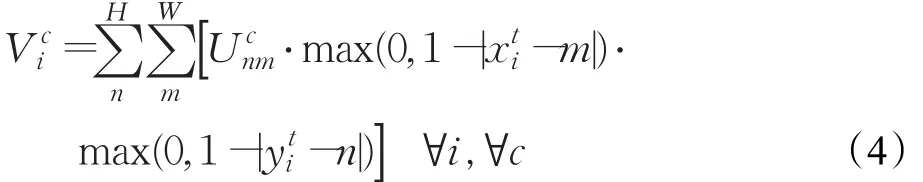
变换图像It的生成还需要满足可微分性，这样才能够通过后向传播中的梯度下降算法进行有效的训练。为了保证变换后输出图像的准确性，采样器中可以采用双线性插值方法从输入中获取变换输出的像素值。双线性插值的公式为：其中V输出的变换图像通道c上任意像素i，其坐标由Tθ(xt)计算为(x,y)。U则是输入中同样通道坐标为(n,m)的像素。max函数确保插值的邻域仅为(x,y对应输入中(x,y)处的一个像素范围内。该式对于U和x的偏导数分别为：

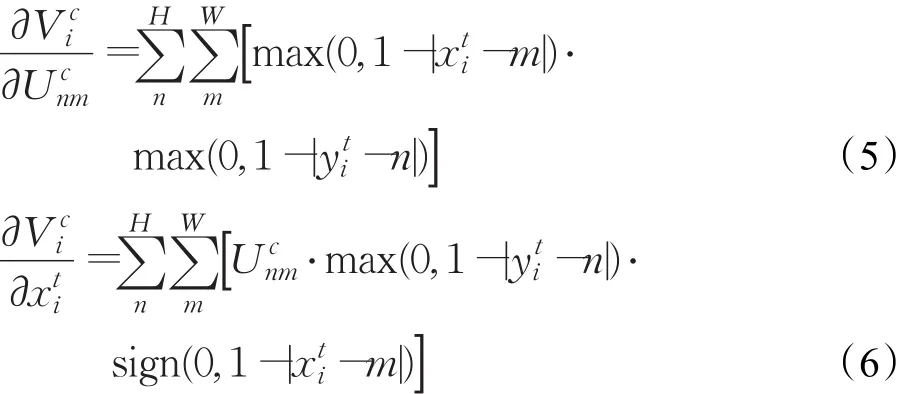
其中sign(·)为符号函数。对于y的偏导数与对x的偏导数是相似的。公式使得梯度的后向传播从输出流向输入的前级网络U。而公式则使得梯度的后向传播从输出流向STN中的网格生成器和定位网络。因此，不断地运用基于梯度下降的优化算法，便可以令STN不断地得到训练。鉴于STN完全可微分，其可以作为一个通用的神经网络层添加到整个网络的任意地方。通常STN网络仅需使用很小规模的CNN来进行学习，即很少的计算量，但对整个分类器准确度的提升具有显著的效果。

4.2 具体实现结构

由这三个模块组成的STN由于在整体上都是可微分的，自然便可以作为一个功能层无缝地添加到已有的神经网络中。为了提高图像块的匹配率，本文将其作为对每个图像块的预处理层。具体的结构见图6。

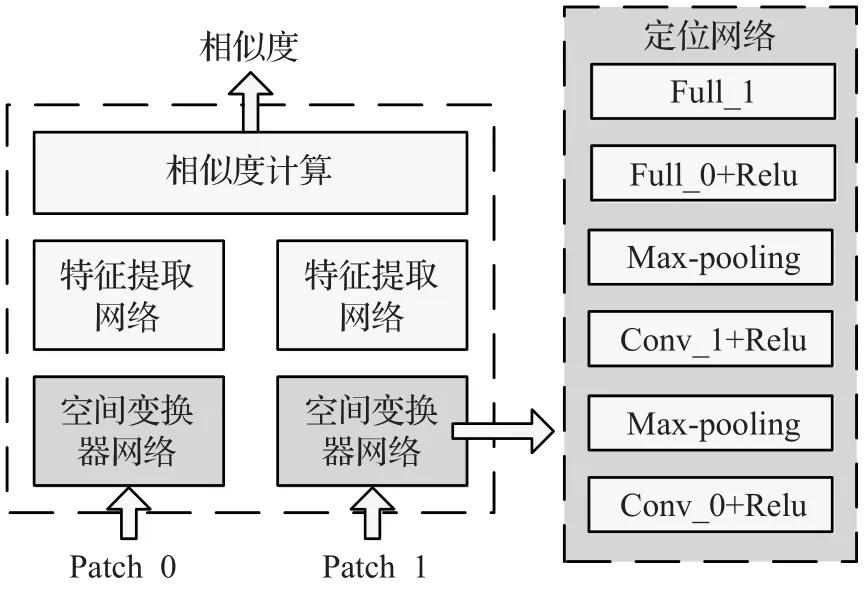
图6 加入空间变换器网络的孪生网络

在图中的定位网络中，使用的卷积网络分别为Conv_0（32，3）和Conv_1（64，4），其中前后数字分别为滤波器数量和尺寸。使用的全连通网络分别为Full_0（6 400，64）和Full_1（64，6），其中前后数字分别为输入和输出神经元的数量。最后输出的是6个仿射变换的参数。从前馈的角度来看，STN形成了一个具有学习能力的非线性函数：

其中函数 f是一个可学习的几何参数预测器，即STN中的定位网络部分。通过它便可以预测出输入图像与基准图像之间的几何变换。通常这一几何变换是能够包含平移、缩放和旋转在内的仿射变换。在训练阶段，STN是作为一种弱监督学习的形式存在的。也就是说对于所有输入的样本对，只给出了该样本对的是否匹配的标签，而并不知道样本中实际目标的相对于基准的变换。通过大量的训练，STN需要自主地学习来获得这些信息。

在STN的使用中有两个需要注意的地方，一是定位网络要足够大才能比较好地捕捉到图片的抽象特征，可以参考论文中的结构，二是空间变换器的初始化要满足一开始输出图片和输入图片相同，否则一开始就随机对图片做变换很难训练得到比较好的结果。以仿射变换为例，空间变换器最后一层输出6个参数的全连接层初始化的权值为0，偏置为[1 0 0 0 1 0]，这样能够开始时保证输出图像和输入图像一样。

5 实验与结果

5.1 实验数据与平台

实验的平台为一台PC机，主要配置为：Intel E5 2643 V2，16GB DDR3 RAM，Intel 240 G SSD，NVIDIA GTX 1070。实现的代码均采用Python语言在Pytorch框架下完成。利用CUDA和cudnn提供的并行加速能力实现快速的训练和识别任务。

为了验证所设想的深度神经网络模型，采用GTSRB路标数据集[14]来完成测试。该数据集中包含了43个不同的路标在各种条件下的样本图像。整个数据集分为训练集和测试集。训练集共有26 640个样本图像，测试集共有12 569个样本图像。这些样本图像具有各种不同的尺寸，而神经网络系统要求的图像为统一的尺寸。为此，在载入图像时对图像进行不同比例的缩放，统一尺寸为48×48个像素。通过生成算法，为孪生网络提供53 280个正负样本对的索引以及每对样本是否匹配的标签，通过它们可以用来进行训练和验证。

在构建神经网络模型之前，还必须完成相关的数据准备工作。对于巨大的训练样本来说，在训练时为神经网络模型快速地提供数据是至关重要的。为了加快训练的速度，在一般情况下都是采用高性能的GPU来进行训练。如果训练的样本仍然存储于硬盘（即使是非常快速的固态硬盘）上，则其读取速度会跟不上GPU的计算速度。导致的结果就是，GPU在很大一部分时间上是处于空闲状态的。为了很好地解决这个问题，则可以将训练样本存储于内存上。在Linux下，采用tmpfs文件系统格式在内存上创建一个临时文件系统。然后，在该文件系统下采用基于键值对的leveldb数据库存储每个图像的像素值及其编号。在存储之前，还需要将表示48×48尺寸patch的numpy数组进行序列化。读取的代码则非常简单，只需要使用db.get函数即可取出指定编号的序列化后的图像。使用pickle.loads函数还原到原始的图像。通过实验表明，在该方法下GPU始终处于满负荷的工作状态。

5.2 实验结果

在测试样本输入到神经网络之前，所有输入的彩色样本都经过归一化处理，分别采用了两种方法来实现。第一种是零均值归一化，公式为z=(x-u)/σ，其中u和σ分别为各个颜色通道上的颜色均值和方差。第二种方法则为对比度受限的自适应直方图均衡化（CLAHE）。在实验中，对原始样本图像进行四种不同变换组合，以及加入空间变换器网络（STN）。对孪生网络的训练相比于单组的网络并没有太多的特别之处，因为孪生网络中的两组深度网络结果相同且共享权值的。因此，利用在前向计算中得到的损失函数，在进行后向误差传播方式的优化时仅需作用于一组网络即可。在训练时对神经网络的优化采用随机梯度下降（SGD）方法和Adam方法，设置它们的学习率分别为0.01和0.001，SGD方法中的动量（momentum）设置为0.9。训练中每批次的样本对数量为512，这样可以充分利用到GPU中的显存，以加快训练速度。对整个网络训练200次，即200个Epoch，得到的损失函数曲线见图7。

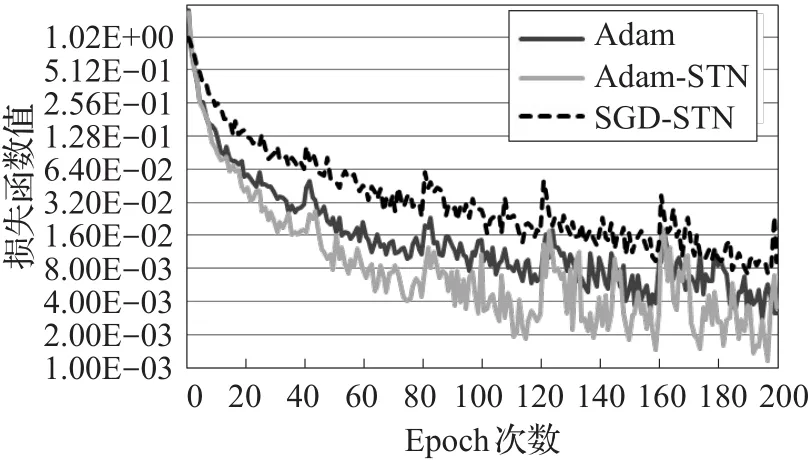
图7 训练的损失函数曲线

Adam方法能够在训练的过程中自适应地调整各个参数的学习率，可以很快地收敛。而SGD方法虽然设置了比Adam方法更高的学习率，但其收敛的速度仍然比Adam方法慢很多。这充分体现了Adam方法具有非常优异的自适应学习率调整能力，这使得其非常适合于高维度和大数据集的非凸优化。从图中可以看到，使用了STN方法得到了更快的收敛速度。这是由于作为前端的STN会逐步地学习经验，对输入图像进行调整，从而提高后端分类器的效果。

另外，还可以看到，每隔40个epoch在损失函数曲线上会存在一个小的波动。这是因为每隔40个epoch，会重新生成一次样本对，以及对样本对重新进行随机的变换。这一过程可以称为重采样过程。对于前次已训练的很好的神经网络，新生成的训练样本对会产生一点小小的冲击。但随着神经网络不断的学习，这种影响会逐渐变小。训练样本对的重采样是训练数据扩充的重要手段。当数据集本身比较庞大时，为每个样本都进行不同程度的位移、缩放和旋转时，那么训练样本将会成几何级的增长。因此，随机地对样本进行变换，并在训练过程中重采样，可以在不增加太多训练时间的情况下，使分类器神经网络获得更好的性能。

在训练时，每隔10个epoch便会对学习得到神经网络参数进行存储，以供测试之用。从所有保存的神经网络参数中确定出最好的一组神经网络参数。在使用和不使用STN的情况下，所得到的测试结果见表2。

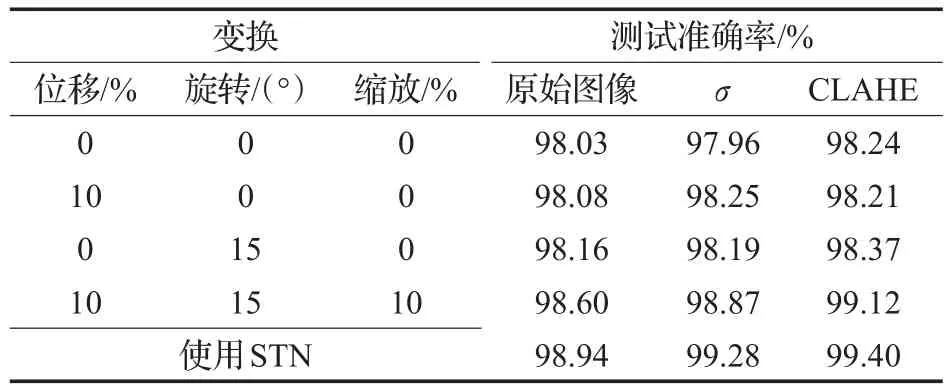
表2 测试结果

从表1中可以看到，随着使用的随机变换种类越多，对测试样本集得到的准确率会更高。这充分说明在训练时样本的多样性对于神经网络的训练是至关重要的。因为在训练中所学习到的对样本的各种变形可能在测试或者实际应用中就有可能遇到。同时，也对比了采用两种归一化方法，以及不采用归一化方法的测试，显然进行归一化处理后的样本能达到更好的效果。而CLAHE方法也要优于零均值归一化方法。表中的最后一行为在同时使用位移、旋转和缩放的条件下加入STN方法的结果，STN方法的使用进一步提高了识别的准确率，这说明STN能够很好地对原始的输入样本进行校正，使其能够更好地分类。

图8给出了原始图像和经过STN变换后的结果。图8（a）选取了限速30 km的标志的8个不同的输入图像的对比。图8（b）则选取了其他8种不同标志的对比。可以发现，STN会进行各种不同程度的自适应的仿射变换，使它们尽可能地趋近训练时使用的基准样本图像。可以看到图8（a）的第二行STN变换得到的限速30 km标志图像都变得与图4（a）中的基准相似。由于仿射变换本身便是偏移、缩放以及旋转的合成，所以只要由多层卷积和全连通网络构成的定位网络识别出了这些变换并预测出仿射变换参数，便可以使用网格生成器和采样器对原始输入图像进行校正。经过STN处理之后的图像变得更容易为后续的分类器神经网络所识别。

图8 （b）STN结果对比

最后与近年来针对交通标志识别的主要方法进行了对比，结果见表3。Committee of CNNs[15]方法为当前取得测试结果最好的方法。该方法利用了深度卷积神经网络和多层感知器进行组合来选择最可能的识别结果，达到了99.46%。但该方法既使用了深度卷积神经网络，又使用了多层感知器，在训练和预测的时间上的花费都比较高。其利用两块GTX 480和两块GTX580，训练时间达37小时以上。WELM-AdaBoost采用了多分类AdaBoost算法，并辅以ELM模型作为弱分类器来进行快速的学习和识别，也达到了99.12%的不错的准确率。Multi-Scale CNNs方法与本文中所提出的孪生神经网络中的单组网络结构很相似，只达到了98.31%的准确率。本文所提孪生神经网络方法采用简练的神经网络结构，取得了仅次于Committee of CNNs方法的结果，准确率达到了99.40%。在实际应用中这样的差距是微乎其微的，且结果都好于人工识别98.84%的准确率。本文方法在单个GTX 1070的支持下只需要很少的训练时间，约3个小时。因此综合考虑，本文的方法是一种性能优异的分类器方法。

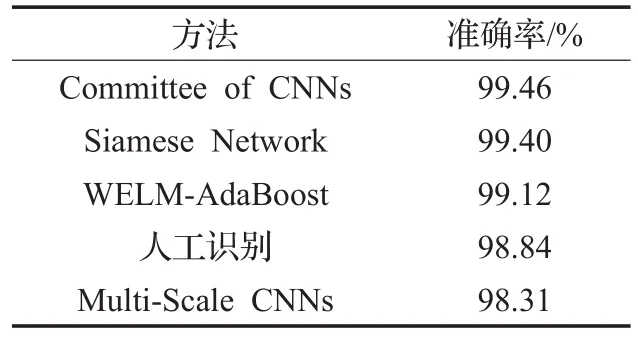
表3 与其他方法结果的对比

6 结束语

本文提出了一种基于孪生神经网络结构的高效分类器。该分类器使用孪生的一对多尺度卷积网络来实现特征提取，并在易分的特征空间中实现两个样本间的相似度计算。为了使孪生神经网络满足分类器的要求，从训练数据集中提取各分类的基准样本，并据此生成孪生神经网络所需的大批量正负样本对。在训练时，还随机地对样本进行了包括平移、旋转和缩放在内的变换，以加大神经网络学习的样本的多样性。在卷积网络的前端无缝地增加了空间变换器网络，在使用时增强神经网络对各种变换的不变性，从而提高了分类器的准确率。将所提的分类器应用于具有复杂环境条件下的交通标志识别任务。通过对GTSRB数据集的实现验证，该分类器能够到达极好的准确率，并能够高效地运行。

：

[1]Greenhalgh J，Mirmehdi M.Real-time detection and recognition of road traffic signs[J].IEEE Transactions on Intelligent Transportation Systems，2012，13（4）：1498-1506.

[2]徐岩，王权威，韦镇余.一种融合加权ELM和AdaBoost的交通标志识别算法[J].小型微型计算机系统，2017，38（9）：2028-2032.

[3]周俊宇，赵艳明.卷积神经网络在图像分类和目标检测应用综述[J].计算机工程与应用，2017，53（13）：34-41.

[4]王龙，刘辉，王彬,等.结合肤色模型和卷积神经网络的手势识别方法[J].计算机工程与应用，2017，53（6）：209-214.

[5]Paulin M，Mairal J，Douze M，et al.Convolutional patch representations for image retrieval：An unsupervised approach[J].International Journal of Computer Vision，2016，121（1）：1-20.

[6]郭克友，贾海晶，郭晓丽.卷积神经网络在车牌分类器中的应用[J].计算机工程与应用，2017，53（14）：209-213.

[7]Bromley J，Bentz J W，Bottou L，et al.Signature verification using a“SIAMESE”time delay neural network[C]//International Conference on Neural Information Processing Systems.Morgan Kaufmann Publishers Inc，1993：737-744.

[8]Hadsell R，Chopra S，Lecun Y.Dimensionality reduction by learning an invariant mapping[C]//2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.IEEE，2006：1735-1742.

[9]Murphy K P.Machine learning：A probabilistic perspective[M].[S.l.]：MIT Press，2012.

[10]Krizhevsky A，Sutskever I，Hinton G E.ImageNet classification with deep convolutional neural networks[C]//International Conference on Neural Information Processing Systems.Curran Associates Inc，2012：1097-1105.

[11]Chen Y，Chen Y，Wang X，et al.Deep learning face representation by joint identification-verification[C]//International Conference on Neural Information Processing Systems.[S.l.]：MIT Press，2014：1988-1996.

[12]Srivastava N，Hinton G，Krizhevsky A，et al.Dropout：a simple way to prevent neural networks from overfitting[J].Journal of Machine Learning Research，2014，15（1）：1929-1958.

[13]Jaderberg M，Simonyan K，Zisserman A，et al.Spatial transformer networks[C]//International Conference on Neural Information Processing Systems.[S.l.]：MIT Press，2015：2017-2025.

[14]Houben S，Stallkamp J，Salmen J，et al.Detection of traffic signs in real-world images：The German traffic sign detection benchmark[C]//InternationalJointConference on Neural Networks.IEEE，2008：1-8.

[15]Ciresan D，Meier U，Masci J，et al.A committee of neural networks for traffic sign classification[C]//InternationalJointConferenceonNeuralNetworks.IEEE，2011：1918-1921.