基于类内距离参数估计的文本聚类评价方法

牛奉高，张荣杰

(山西大学 数学科学学院,山西 太原 030006)

0 引言

聚类是数据挖掘处理中的重要任务之一,它可以发现隐藏数据集中的簇,标记出感兴趣的分布或模式。聚类问题是将一组对象分成若干个类,使类内的对象尽可能有最大的相似性,不同类之间的对象尽可能有最大的相异性。聚类过程作为一种无监督的学习过程,因为没有预先定义的分类或示例来表明数据集中哪种期望的关系是有效的,多数聚类算法依靠假设和猜测进行[1]。因此,最终的聚类结果需要进行有效性验证和质量评价。

聚类有效性评价一直是聚类领域的热门问题。广义上讲,聚类有效性评价包括聚类质量的度量、聚类算法适合某种特殊数据集的程度,以及某种划分的最佳聚类数目[2]。它就是通过建立一个指标函数,即聚类有效性评价指标,当指标函数值最优时,对应的聚类划分、聚类算法以及聚类数目最优。

目前,大多数学者对于聚类有效性评价的研究或是对部分评价指标从不同角度进行比较[3-5];或是针对某个指标进行改善,提出新的指标,并基于实验验证新指标的性能优于之前提出的那个指标[6-8];或是确定最佳聚类数等来展开[9-11]。只有很少一部分学者将聚类有效性评价和参数统计方法结合起来进行研究,例如Dubes[12]使用卡方统计量测试不同因素对聚类评价指标行为的影响,当然,使用统计测试去验证实验结果在聚类中是不常见的做法;王钰、王瑞波[13]通过确定F值的分布函数,来确定F值的置信区间,后期对F值的分布函数继续深入研究,提高了F值置信区间的准确度;郑军、王巍等[14]提出了运用统计学当中的参数估计方法,根据类间距离信息对其分布规律中的数字特征进行参数估计,基于估计的结果确定类间距离合理的取值范围,将不合理的聚类进行调整,有效地提高了聚类结果的准确性。但是,当聚类类别数过小或等于真实类别数时,难以使用基于类间距离参数估计的文本聚类评价方法对聚类结果进行改善。因此,文章提出了基于类内距离参数估计的文本聚类评价方法。

1 相关知识概述

1.1 文本聚类

文本聚类是对文本数据集在主题粒度上进行划分,把具有相同主题的文本聚成一类。在对文本数据集进行聚类之前,需要对文本进行预处理。例如中文文本需要进行分词、去除停用词、特征选择等预处理过程。

其中,常用的特征选择的方法为词频-逆词频(TF-IDF)算法,该算法利用每个词的词频与逆词频的乘积来确定权重,将每篇文档中的词语依据权重进行排序,选取权重较大的词来代表该文本。

经过预处理后的文本文档,在聚类之前需转化为计算机可处理的形式,常用的有效方法之一是向量空间模型(VSM),行向量代表每篇文档,列向量代表每个特征词,行向量每个维度上的数值为每个特征词在该篇文档上的权重。对于任意给定的文本数据集,设文本文档的总数为n,经向量空间表示为X=(x1,x2,…,xn)′, 设聚类算法将其分为K类C=(c1,c2,…,cK)。

1.2 类内及类间距离

选定某聚类算法对文本数据集进行聚类后,需要用一种客观公正的评价方法对聚类结果的有效性进行评判。常用的聚类有效性评价方法包括外部评价法、内部评价法和相对评价法。一般来说,聚类有效性评价方法主要基于两个原则:紧致性,即类内成员必须尽可能地相互靠近;分离性,即类间成员必须尽可能地相互远离。而紧致性和分离性主要依据类内距离和类间距离进行度量,即类内距离越小则类内越紧致,类间距离越大则类间越分离[2]。

常见的确定类间距离的方法包括最近邻距离(Nearest neighbor)——以两类中距离最近的两个个体之间的距离作为类间距离;最远邻距离(Furthest neighbor)——以两类中距离最远的两个个体之间的距离作为类间距离;重心距离(Centroid cluster)——以两类变量的均值向量之间的距离作为类间距离等。常见的确定类内距离的方法包括以类中距离最远的两个个体之间的距离作为类内距离即直径;类内个体到类中心向量的距离作为类内距离等。文章的类内距离是基于后者计算的,其中类中心为该类的质心即类内所有对象的算术平均值。文章中涉及的所有距离均为欧氏距离。

2 基于类内距离参数估计的文本聚类评价方法

2.1 类内距离分布规律的研究方法

由于任意一个聚类算法都不能保证将所有待聚类对象准确地分到它所属的那类,因此,文章参考郑军、王巍等[14]确定类间距离分布函数的方法来确定类内距离的分布函数,并依据类内距离的分布函数得到类内距离的合理取值范围。若某些类内距离偏离合理的取值范围,则对应的那些文本聚类对象极有可能被错分到其他类中。类内距离分布规律的研究方法采用的是经典的(参数)统计估计方法。

2.2 类内距离的分布函数

尽管TF是离散的,但是由于再训练等原因,IDF值经常发生变化,故文本向量中每个维度的值也是不断发生变化的。因此,基于文本向量计算得到的类内距离可以看作是一个随机变量。此外,由于类内距离是类内对象到类中心的距离,文本向量和中心向量的维数很大,而且单个维度的值对类内距离计算结果的影响是微小的。故由中心极限定理的成因(若一个随机变量的取值是由大量相互独立的随机因素共同影响形成的,然而其中的任意影响因素对于该随机变量的作用是微小的,则该随机变量往往近似服从正态分布)可知类内距离是近似服从正态分布的变量。文章中我们设类内距离服从正态分布N(μ,σ2),其中μ和σ2为分布函数的两个参数。基于类内距离参数估计的文本聚类评价方法的第一步,就是对这两个参数进行参数估计,确定出类内距离的分布函数;第二步,根据分布函数确定出类内距离的合理取值范围,对超出范围的文本向量进行调整,并利用聚类评价指标来验证聚类调整的有效性。

2.3 类内距离分布的参数估计

记类内距离为X,X服从正态分布N(μ,σ2),X的概率密度函数

(1)

(2)

对于σ2,一般取它的无偏估计S2作为其估计值:

(3)

2.4 聚类调整

对于任意给定的文本数据集,利用聚类算法对其进行聚类得到原始的聚类结果,并输出类内距离。聚类的目的是使类内对象相似性尽可能大即类内距离尽可能小,故类内距离越大聚类效果越差。因此,只对类内距离过大的情况进行调整,最后利用聚类评价指标对最终调整结果进行评价。具体的聚类调整步骤如图1。

需要注意的是对于开始未能成功调整的文本向量,后期不再进行调整,基于类内距离参数估计的文本聚类评价方法只能成功调整超过正常范围的部分文本向量。

3 实验

3.1 数据集——谭松波的中文文本分类语料[16]

文章选用了一开放的中文数据集——谭松波的中文文本分类语料,它不仅包含大的分类,例如经济、运动等等,每个大类下面还包含具体的小类,例如运动包含篮球、足球等等。文章选用IKAnalyzer分词器进行分词和去除停用词,对数据集分词和去除停用词后,利用TF-IDF方法进行加权,基于权重大小进行特征选择,最终生成篇词矩阵。

3.1.1 60篇文本文档——从篮球和就业两类中各随机选取30篇

实验从该数据集中随机选取了两小类——篮球和就业,从篮球962篇文档中随机选取了30篇,从就业146篇文档中也随机选取了30篇。将每篇文档中的词语按TF-IDF值从大到小进行排列,选取前10个特征词,若两词共现只保留一个词,共保留了451个特征词。最后利用聚类算法对篇词矩阵进行聚类处理。

3.1.2 200篇文本文档——从篮球和就业两类中各随机选取100篇

为了测试基于类内距离参数估计的文本聚类评价方法在样本量增大后的效果,实验在上述60篇文档的基础上,每类各增加了70篇即每类随机选取了100篇。将每篇文档中的词语按TF-IDF值从大到小进行排列,并选取前10个特征词,共保留了1 269个特征词。最后对篇词矩阵进行聚类处理。

3.1.3 60篇文本文档——从足球和电脑病毒两类中各随机选取30篇

为了防止实验具有偶然性,我们从该数据集中随机选取了另外两类——足球和电脑病毒,从足球1 317篇文档中随机选取了30篇文档,从电脑病毒631篇文档中也随机选取了30篇文本文档,将每篇文档中的词语按TF-IDF值从大到小进行排列,并选取前10个特征词,共保留了434个特征词。最后对篇词矩阵进行聚类处理。

文章将篮球和就业两类中的60个文本向量，200个文本向量分别记为LJ60和LJ200,将足球和电脑病毒两类中的60个文本向量记为ZD60。

3.2 聚类算法

实验采用的是基于最大最小原则的K-means算法和传统的K-means算法,前一种是基于最大最小原则来确定初始类中心,后一种则是随机选取初始类中心。一方面,由于K-means算法是目前应用最广泛的划分聚类算法之一,该算法易于描述,具有时间效率高且适于处理大规模数据等优点[17];另一方面,K-means算法需要预先确定K值且会受到初始聚类中心的影响。

自Creator等[18]发现K-means算法会受到初始聚类中心的影响而收敛于局部最优解的问题之后,初始聚类中心的选择就一直是K-means算法的研究热点。尽管针对初始聚类中心的选取问题,国内外学者提出了许多改进的算法,但是K-means算法始终避免不了初始类中心的影响。而基于类内距离参数估计的文本聚类评价方法的核心思想是通过不断调整不合理对象,来确定聚类中心,进而改善聚类结果。因此,基于该方法对两种算法产生的聚类结果进行调整,易检验该方法的可行性和有效性。

3.3 实验过程

实验主要包括两部分,第一部分,基于类内相似性来确定最佳聚类数;第二部分,基于第一部分的结论,利用K-means算法分别对数据集LJ60、LJ200和ZD60进行聚类,并使用基于类内距离参数估计的文本聚类评价方法对聚类对象进行调整,最后利用聚类指标验证聚类调整的有效性。

3.3.1 聚类数的确定

文章使用高维向量聚类工具——gCLUTO中的可视化山丘来推测聚类数。一个数据矩阵被聚成几类,就会显示为几个山丘,并标记相应的类号,每个山丘的形状为高斯曲线。山丘的高度与类内相似性成正比,体积与类群包含的对象数量成正比,合成的高斯曲线相加在一起形成可视化山丘的地形。山丘的颜色与类内标准差成比例,红色代表低标准差,蓝色代表高标准差。需要注意的是,只有峰顶的颜色是有意义的,在其他所有区域,颜色混合以产生平滑过渡。实验通过山丘的高度、峰顶的颜色可较为准确的推测出正确的聚类数。

实验利用gCLUTO中的可视化山丘得到LJ60、LJ200和ZD60的山丘图。

从图2中可以看出,三个山丘代表三个不同的类群,每个山丘的高度都较高且峰顶颜色为红色。因此,每个类群包含的对象都具有较高的相似性且类内标准差较低,从而可推断LJ60应聚成3类。

从图3中可以看出,尽管该数据矩阵被要求聚成3类,但被清晰地分成两组,两个山丘的高度较高,说明两个类群的类内对象都具有较高的相似性,该可视化图形暗示着LJ200应聚成2类。

从图4中可以看出,尽管该数据矩阵被要求聚成3类,但图中被标号为2的山丘几乎没有高度,被标号为0、1的山丘具有较高的高度,说明只有两个类群的类内对象具有较高的相似性且类内标准差较低。因此,该可视化图形暗示着ZD60聚成2类效果会更好。

3.3.2 聚类调整及其结果检验

该部分基于数据集LJ60、LJ200和ZD60进行了实验。首先,对K-means算法产生的聚类结果与真实类别的分布进行对比,直观上可以看出被调整的文本向量的数量及调整方向;其次,利用R画出类内距离分布的折线图,并详细介绍了每个数据集上的聚类调整过程;最后,利用纯度、F值等指标对聚类结果进行了验证。为了避免初始类中心的选取方式的影响,在实验的最后增加了基于最大最小原则的K-means算法和传统K-means算法的对比实验。

Fig.2 Hill map of LJ60图2 LJ60的山丘图

Fig.3 Hill map of LJ200图3 LJ200的山丘图

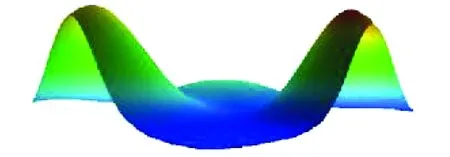
Fig.4 Hill map of ZD60图4 ZD60的山丘图

(1)LJ60

由图2知,基于最大最小原则的K-means算法应将LJ60聚成3类,聚类结果如表1所示。

聚类结果的纯度用Purity表示,聚类结果的纯度值为0.766 7。由表1可以看出,聚类结果1中包含了部分真实类别2的文本,剩余真实类别2的文本被分成了两类。这是因为基于最大最小原则的K-means算法初始类中心选择不当,导致部分真实类别2的文本向量与聚类结果1最终确定的类中心较近而与其他类别的类中心较远。由于数据集本身的特殊性,使得该聚类算法在聚类处理过程中产生了偏差,而自身无法对出现的偏差进行判断和调整。

表1 LJ60聚类结果与真实类别比照Table 1 Comparison of LJ60 clustering results with real categories

利用MATLAB计算出所有类内距离,并利用R画出距离的折线图,结果如图5所示。

Fig.5 Line chart of LJ60 distances’ distribution图5 LJ60类内距离分布折线图

与真实类别相比,聚类结果的平均准确率、召回率及F值如表2所示。

表2 LJ60聚类结果的相关数值Table 2 Related values of LJ60 clustering results

从表2中可以看出,平均准确率、召回率及F值都有所提高。可见,尽管聚类数很小且大于真实类别数,基于类内距离参数估计的文本聚类评价方法仍能通过对聚类中心的调整来减弱初始类中心的选取对K-means算法的影响,提高LJ60的聚类结果的准确性。

(2)LJ200

由图3知,基于最大最小原则的K-means算法应将LJ200聚成2类,聚类结果如表3所示。

表3 LJ200聚类结果与真实类别对照Table 3 Comparison of LJ200 clustering results with real categories

聚类结果的纯度用Purity表示,聚类结果的纯度值为0.79。从比较结果中可知,聚类结果2中包含了部分真实类别1的文本,也是由聚类算法初始类中心选取不当导致的,且自身无法对出现的偏差进行调整。

依据聚类结果计算出所有类内距离,并利用R画出距离的折线图,结果如图6所示。

Fig.6 Line chart of LJ200 distances’ distribution图6 LJ200类内距离分布折线图

与真实类别相比,聚类结果的平均准确率、召回率及F值如表4所示。

表4 LJ200聚类结果的相关数值Table 4 Related values of LJ200 clustering results

从表4中可以看出,平均准确率、召回率及F值都有所提高。可见,当样本量增大后,基于类内距离参数估计的文本聚类评价方法对LJ200仍是可行且有效的。再结合表1和表3可知,当样本量增大后,被成功调整的文本数量也随之增大。

(3)ZD60

为了避免初始类中心的选取方式的影响,实验分别使用基于最大最小原则的K-means算法和传统K-means算法对数据集ZD60进行聚类,并利用基于类内距离参数估计的文本聚类评价方法对两种算法产生的聚类结果进行调整,最后基于实验结果来验证该方法的有效性。为了便于区分,将基于最大最小原则的K-means算法产生的聚类结果和生成的类内分别距离记为ZD60第一聚类结果和ZD60第一类内距离;将传统K-means算法产生的聚类结果和生成的类内距离分别记为ZD60第二聚类结果和ZD60第二类内距离。

由图4知,基于最大最小原则的K-means算法应将ZD60聚成2类,聚类结果如表5所示。

表5 ZD60第一聚类结果与真实类别对照Table 5 Comparison of the first ZD60 clustering results with real categories

聚类结果的纯度用Purity表示,聚类结果的纯度值为0.816 7。从表5可以看出,聚类结果1中包含了部分真实类别2的文本,这是由于基于最大最小原则的K-means算法初始类中心选择不当,导致部分真实类别2的文本向量与聚类结果1最终确定的类中心较近而与其他类别的类中心较远。由于数据集本身的特殊性,使得该聚类算法在聚类处理过程中产生了偏差,而自身无法对出现的偏差进行判断和调整。

计算出所有类内距离后,利用R画出距离的折线图,结果如图7所示。

Fig.7 Line chart of the first ZD60 distances’ distribution图7 ZD60第一类内距离分布折线图

与真实类别相比,聚类结果的平均准确率、召回率及F值如表6所示。

表6 ZD60第一聚类结果的相关数值Table 6 Related values of the first ZD60 clustering results

从表6中可以看出,平均准确率、召回率及F值都有所提高,可见,基于类内距离参数估计的文本聚类评价方法对重新选取的两类别——足球和电脑病毒中的60个文本向量也是可行且有效的。

利用MATLAB自带的传统K-means算法将ZD60聚成2类,聚类结果如表7所示。

表7 ZD60第二聚类结果与真实类别对照Table 7 Comparison of the second ZD60 clustering results with real categories

聚类结果的纯度用Purity表示,聚类结果的纯度值为0.8。从表7可以看出,聚类结果1中包含了部分真实类别2的文本,这是由于传统K-means算法初始类中心选择不当,导致部分真实类别2的文本向量与聚类结果1最终确定的类中心较近而与其他类别的类中心较远。由于数据集本身的特殊性,使得该聚类算法在聚类处理过程中产生了偏差,而自身无法对出现的偏差进行判断和调整。

计算出所有类内距离后,利用R画出距离的折线图,结果如图8所示。

与真实类别相比,聚类结果的平均准确率、召回率及F值如表8所示。

Fig.8 Line chart of the second ZD60 distances’ distribution图8 ZD60第二类内距离分布折线图

平均准确率平均召回率F值调整前085710807917调整后087500833308286

从表8中可以看出,平均准确率、召回率及F值都有所提高。可见,两种K-means聚类算法尽管选取初始聚类中心的方法不同,但基于类内距离参数估计的文本聚类评价方法都能通过对聚类对象的调整来确定聚类中心,减弱初始类中心的选取对K-means算法的影响,提高聚类结果的准确性。

3.4 实验结论

由以上实验结果可知,基于类内距离参数估计的文本聚类评价方法:

(1)不受聚类数的约束,当聚类数较少时,该方法也是可行的;

(2)无论基于类内相似性确定的最佳类别数与真实的类别数是否相同,都能通过对超出类内距离合理取值范围的文本向量进行调整,减弱初始类中心的选取对K-means算法的影响,提高聚类结果的准确性;

(3)随着样本量的增大,被成功调整的文本数量也随之增大；

(4)不受K-means算法初始类中心选取方式的影响,不管是基于最大最小原则确定初始类中心还是随机选取初始类中心,该方法都是有效的。

4 结论

文章提出了基于类内距离参数估计的文本聚类评价方法,该方法弥补了当聚类类别数过小或与真实类别数相同时,难以使用基于类间距离参数估计的文本聚类评价方法对聚类结果进行改善的缺陷。首先,文章在类内距离近似服从正态分布的基础上,运用极大似然估计方法对类内距离分布函数的参数进行了估计;其次,文章基于估计的结果确定类内距离的合理取值范围,对超出范围的文本向量依据类内距离大小依次进行调整,并用流程图展示了具体的聚类调整过程;最后,文章在LJ60、LJ200和ZD60上从不同聚类数、样本量、数据集、聚类算法四个角度进行了对比实验,可知基于类内距离参数估计的文本聚类评价方法不受聚类类别数大小、与真实类别数是否相同、K-means算法初始类中心的选取方式的影响,基于纯度、F值等指标验证了该方法的可行性和有效性。接下来的工作可以将基于类内距离参数估计的文本聚类评价方法和基于类间距离参数估计的文本聚类评价方法结合起来,可大大改善聚类结果,这将是作者进一步的研究方向。

参考文献：

[1] 杨燕,靳蕃,Mohamed K.聚类有效性评价综述[J].计算机应用研究,2008,25(6):1630-1632.DOI:10.3969/j.issn.1001-3695.2008.06.007.

[2] 张惟皎,刘春煌,李芳玉.聚类质量的评价方法[J].计算机工程,2005,31(20):10-12.DOI:10.3969/j.issn.1000-3428.2005.20.005.

[3] Arbelaitz O,Gurrutxaga I,Muguerza J,etal.An Extensive Comparative Study of Cluster Validity Indices[J].PatternRecognition,2013,46(1):243-256.DOI:10.1016/j.patcog.2012.07.021.

[4] Gurrutxaga I,Muguerza J,Arbelaitz O,etal.Towards a Standard Methodology to Evaluate Internal Cluster Validity Indices[J].PatternRecognitionLetters,2011,32(3):505-515.DOI:10.1016/j.patrec.2010.11.006.

[5] Brun M,Sima C,Hua J,etal.Model-based Evaluation of Clustering Validation Measures[J].PatternRecognition,2007,40(3):807-824.DOI:10.1016/j.patcog.2006.06.026.

[6] Starczewski A.A New Validity Index for Crisp Clusters[J].PatternAnalysisandApplications,2017,20(3):687-700.DOI:10.1007/s10044-015-0525-8.

[7] Saha S,Bandyopadhyay S.Performance Evaluation of Some Symmetry-based Cluster Validity Indexes[J].IEEETransactionsonSystems,Man,andCybernetics,PartC(ApplicationsandReviews),2009,39(4):420-425.DOI:10.1109/TSMCC.2009.2013335.

[8] Wani M A,Riyaz R.A New Cluster Validity Index using Maximum Cluster Spread based Compactness Measure[J].InternationalJournalofIntelligentComputingandCybernetics,2016,9(2):179-204.DOI:10.1108/IJICC-02-2016-0006.

[9] 刘远超,王晓龙,刘秉权.一种改进的K-means 文档聚类初值选择算法[J].高技术通讯,2006,16(1):11-15.DOI:10.3321/j.issn:1002-0470.2006.01003.

[10] 王勇,唐靖,饶勤菲,等.高效率的K-means 最佳聚类数确定算法[J].计算机应用,2014,34(5):1331-1335.DOI:10.11772/j.issn.1001-9081.2014.05.1331.

[11] Halkidi M,Batistakis Y,Vazirgiannis M.On Clustering Validation Techniques[J].JournalofIntelligentInformationSystems,2001,17(2):107-145.DOI:10.1023/A:101280161.

[12] Dubes R C.How Many Clusters are best?-an Experiment[J].PatternRecognition,1987,20(6):645-663.DOI:10.1016/0031-3230(87)90034-3.

[13] Yu W,Ruibo W,Huichen J,etal.Blocked 3×2 Cross-validatedt-test for Comparing Supervised Classification Learning Algorithms[J].NeuralComputation,2014,26(1):208-235.DOI:10.1162/NECO-a-00532.

[14] 郑军,王巍,杨武,等.基于类间距离参数估计的文本聚类评价方法[J].计算机工程,2009,35(9):37-39.DOI:10.3969/j.issn.1000-3428.2009.09.013.

[15] Cristianini N,Shawe-Taylor J,Lodhi H.Latent Semantic Kernels[J].JournalofIntelligentInformationSystems,2002,18(2):127-152.DOI:10.1023/A:1013625426931.

[16] 谭松波.中文文本分类语料[EB/OL].http:∥www.datatang.com/data/11970,2017-05-14.

[17] 王千,王成,冯振元,等.K-means 聚类算法研究综述[J].电子设计工程,2012,20(7):21-24.DOI:10.3969/j.issn.1674-6236.2012.07008.

[18] Creator R,Kaufman L,Source R,etal.K-means Type Algorithms:A Generalized Convergence Theorem and Characterization of Local Optimality[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,1984,6(1):81-87.DOI:10.1109/TPAMI.1984.4767478.