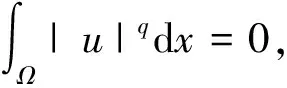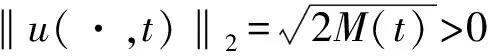具有齐次Neumann边界条件的抛物p-Laplace方程解的爆破以及不熄灭问题
2018-05-21贺艺军周芬王华
贺艺军,周芬,王华
(1.山西大学 数学科学学院,山西 太原 030006;2.太原科技大学 应用科学学院,山西 太原 030024)
0 引言
设Ω是Rn中的有界光滑区域,1
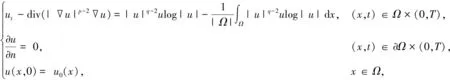
(1)
其中u0满足下述条件(*)
(*)
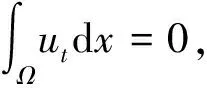
(2)
方程
ut-div(|u|p-2u)=f(u)
称为非牛顿渗流方程或p-Laplace抛物型方程, 它出现在核科学、人口动力学、化学反应、生物科学等应用科学的许多数学模型中,可参看文献[1-2] 以及其后的参考文献。
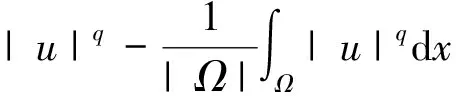
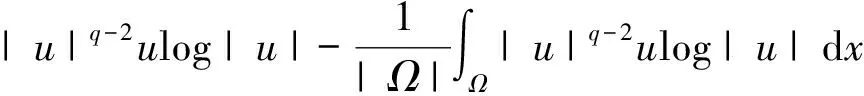
正如文献 [3],我们给出问题 (1) 的弱解的定义:

(3)
类似于文献 [10], 通过Galerkin方法,可得问题(1)弱解的局部存在性。 令u为问题 (1) 的弱解, 接下来, 我们将给出主要的结论。
对于u∈W1,p(Ω){0}, 定义能量泛函E(u)为
我们有下面解的爆破和不熄灭的定理。
定理1 (爆破)设u是问题 (1) 的解,并且1
定理2 (不熄灭) 设u是问题 (1) 的解,并且1 这一节我们给出定理1和定理2的证明。 在给出定理1和定理2的证明之前, 我们给出三个引理。 引理1 如果u是问题(1)的解, 则能量泛函E(u(t))是非增的, 并且有 (4) 证明对能量泛函E(u(t))关于t求导并且结合 (1) 得 对上面的等式从0到t积分, 我们可以得到 (4). 令 引理2 设1 (5) 证明结合(1)和(2),很容易得出 (6) 由于q≥p,故有 M′(t)≥-qE(u). (7) 再由引理1以及E(u0)≤0,有 引理3 假设1 (8) 证明由Hölder不等式以及 (6), (9) 此外,再由 (5), 由上面的两个不等式可以得到结论。 定理1的证明我们通过反证法来给出证明。 假设问题 (1) 的解u对于所有的t>0存在。 首先我们断言 对于任意的t0>0成立。 若上式不成立, 则存在t0>0使得 因此 (10) 由 (10) 以及q>2可知存在t*≥t0, 使得 当t≥t*. 此外,由引理3可得, 当t≥t*, 从而当t≥t*时有H(t)>0,H″(t)>0. 以及 于是当t≥t*时,G(t)是一个凹函数,从而有 G(t)≤G(t*)+G′(t*)(t-t*), 当t≥t*. 定理2的证明由(1), (2) 以及E(u)的定义可得 (11) 由(4),(11)并注意到q≤p<2,我们有 若q=p, 则M′(t)≥-pE(u0). 积分后可得 M(t)≥M(0)-ptE(u0), 由于E(u0)≤0, 故得到M(t)>0对于所有t>0成立。 因而也有M(t)>0对于所有t>0成立。 于是我们证明了定理2。 参考文献: [2] Wu Z,Zhao J,Yin J,etal.Nonlinear Diffusion Equations[M].World Scientific Publishing Company Incorporated,2001.DOI: 10.1142/9789812799791. [3] Guo B,Gao W.Non-extinction of Solutions to a Fast Diffusivep-Laplace Equation with Neumann Boundary Conditions[J].JMathAnalAppl,2015,422(2):1527-1531.DOI: 10.1016/j.jmaa.2014.09.006. [4] Hao A,Zhou J.Blow-up,Extinction and Non-extinction for a Nonlocalp-biharmonic Parabolic Equation[J].ApplMathLett,2017,64:198-204.DOI:10.1016/j.aml.2016.09.007. [5] Qu C,Bai X,Zheng S.Blow-up Versus Extinction in a Nonlocalp-Laplace Equation with Neumann Boundary Conditions[J].JMathAnalAppl,2014,412(1):326-333.DOI: 10.1016/j.jmaa.2013.10.040. [6] Jazar M,Kiwan R.Blow-up of a Non-local Semilinear Parabolic Equation with Neumann Boundary Conditions[J].AnnInstHPoincaréAnalNonLinéaire,2008,25(2):215-218.DOI: 10.1016/j.anihpc.2006.12.002. [7] Lin Z,Xie C.The Blow-up Rate for a System of Heat Equations with Neumann Boundary Conditions[J].ActaMathSin(EnglSer),1999,15(4):549-554.DOI: 10.1007/s10114-999-0086-0. [8] Deng K.The Blow-up Behavior of the Heat Equation with Neumann Boundary Conditions[J].JMathAnalAppl,1994,188(2):641-650.DOI:10.1006/jmaa.1994.1450. [9] El Soufi A,Jazar M,Monneau R.A Gamma-convergence Argument for the Blow-up of a Non-local Semilinear Parabolic Equation with Neumann Boundary Conditions[J].AnnInstHPoincaréAnalNonLinéaire,2007,24(1):17-39.DOI: 10.1016/j.anihpc.2005.09.005. [10] Nhan L C,Truong L X.Global Solution and Blow-up for a Class of Pseudop-Laplacian Evolution Equations with Logarithmic Nonlinearity[J].ComputMathAppl,2017,73(9):2076-2091.DOI: 10.1016/j.camwa.2017.02.030. [11] Zhao J.Existence and Nonexistence of Solutions forut=div(|u|p-2u)+f(u,u,x,t)[J].JMathAnalAppl,1993,172(1):130-146.DOI: 10.1006/jmaa.1993.1012. [12] Yin J,Jin C.Critical Extinction and Blow-up Exponents for Fast Diffusivep-Laplacian with Sources[J].MathMethodsApplSci,2007,30(10):1147-1167.DOI: 10.1002/mma.833.1 定理的证明