基于激光干涉测量的液体高脉冲压力校准*

杨 军,史 博,樊尚春,李 程,李 博,黄日恒

(1.北京航空航天大学仪器科学与光电工程学院,北京 100083;2.北京长城计量测试技术研究所,北京 100095)

压电式压力传感器具有灵敏度高、动态特性好等优点，被广泛应用于动态压力测量，如枪炮膛压变化以及炮口冲击波压力、爆炸冲击波压力、发动机内流压力脉动等的测量。但对于相当一部分压电式压力传感器，如不使用高阻抗电荷放大器，就难以采用静态校准方法进行校准；特别是近年来发展非常迅速的内置放大器的压电传感器(如ICP压力传感器)，电荷泄漏时间较短，更是无法进行静态校准。这时一般通过脉冲压力(半正弦压力)校准装置进行灵敏度校准。另外，有一些价格昂贵的高压传感器使用寿命却很有限，如使用静态校准，长时间的加载会严重影响到传感器的实际可使用寿命,此时，如使用脉冲压力校准装置进行准静态校准，在每个压力点只需要加载几毫秒，将大幅度缩短校准中的加载时间，延长传感器使用寿命。

落锤式液体脉冲压力发生器[1-2]是最常用的脉冲压力校准器。落锤式液体脉冲压力发生器利用自由落体撞击密闭油缸上的活塞，在油缸内形成波形类似于半正弦的脉冲压力，结构简单，动态压力幅值高(最高可达1 000 MPa)，脉冲宽度多在(1～15) ms范围内，特别适用于高压传感器的灵敏度校准，已经形成相关的产品[3]；但校准使用中基本都采用比较法(使用参考传感器)，参考传感器的量值溯源问题长期没有得到有效解决。因此，国际上相当一部分研究人员更倾向于把这类设备当成专用的测试设备而不是计量标准设备。PCB公司与南京理工大学等[4]曾尝试利用牛顿第二定律以及加速度计或动态力传感器等来计算脉冲压力，但加速度计需要再校准，动态力溯源问题也没有得到解决，同时摩擦力、附加惯性力等系统误差没有得到必要的分析修正。为了解决液体脉冲压力的可溯源问题，近年来在欧洲计量组织EURAMET项目“Traceable Dynamic Measurement of Mechanical Quantities”[5]的支持下，欧洲多个国家计量技术研究机构对激光干涉仪在液体脉冲压力校准中的应用进行了研究。意大利国家计量院INRIM与土耳其国家计量院UME研究基于牛顿第二定律以及加速度激光干涉测量的脉冲压力校准方法[6-7]，但没有见到关于摩擦力、惯性质量块(锤体)加速度分布等系统误差的研究报道。芬兰国家计量院MIKES研究了基于胡克定律与液体压缩比激光干涉测量的脉冲压力校准方法[8]，该方法要求液体的体积弹性模量非常稳定，对温度、排气等要求非常高，线性范围小，因此实用性较差。对这3套装置报道的校准压力范围在(100～500) MPa之间，没有更小或更大压力幅值的实验情况，不能满足(10～100) MPa常用液体动态压力测量校准需求。德国联邦物理研究院PTB研究了基于折射率-压力模型的水脉冲压力激光干涉测量的方法[9]，分析了基本原理与方法，实验的范围更小，严重的非线性问题有待解决[10]。

本文中，介绍了北京长城计量测试技术研究所研制的激光干涉法液体脉冲压力校准装置，在落锤式液体脉冲压力发生器上，采用基于牛顿第二定律的激光干涉法脉冲压力幅值测量，实现了脉冲压力的可靠溯源；对摩擦力、压力分布、锤体加速度分布等误差进行了系统分析、优化与实验，幅值校准扩展不确定度在1.8%以内；通过发生器结构的系统优化，使激光干涉法液体脉冲压力幅值范围覆盖(10～500) MPa，并有望进一步扩展。

1 基本原理与结构

激光干涉法液体脉冲压力校准,采用自由下落的锤体冲击液压活塞,压缩密闭液压腔中介质并反弹产生半正弦压力脉冲信号，由锤体与活塞的动力学分析建立压力与锤体、活塞加速度、质量以及活塞面积等之间的关系模型，并通过激光干涉法精密测量锤体的加速度，从而实现脉冲压力的测量并溯源到长度、时间、质量等基本量。其核心结构原理如图1所示。

校准装置除了核心的液体脉冲压力发生器与激光干涉测量系统，还包括数据采集分析及控制系统、地基与隔振平台等辅助部分。在进行脉冲压力激光干涉测量中，通过对摩擦力、液体压力分布不均、加速度分布不均等因素进行分析并补偿修正，提高压力测量计算的准确度。安装在液压缸侧壁的被校压力传感器(测试系统)感受压力脉冲，输出电信号被同步采集，电信号曲线上的幅值与激光干涉系统测量计算得到的压力脉冲幅值进行比较,即可得到被校压力传感器(测试系统)的灵敏度。

2 液体脉冲压力发生器

基于自由落锤冲击的活塞式液体脉冲压力发生器主要包括落锤实验装置和液压活塞系统。落锤实验装置提升并释放的自由落体的重锤冲击液压活塞系统的活塞，活塞受到冲击在密闭液压缸中压缩液体并反弹形成一个类似半正弦的压力脉冲。用于激光干涉法测量校准的落锤式液体脉冲压力发生器除了实现所需的幅值与脉宽外，对波形、横向运动、摩擦力、附加惯性质量等都提出了新的要求。如为了避免脉宽调节使用缓冲垫引入的难以确定的新的附加质量及相应的惯性力，校准装置将不再使用缓冲垫。根据朱明武等提出的设计规律，无缓冲垫情况下脉冲压力的幅值、脉宽以及活塞的位移与锤体质量、提升高度、活塞截面积、液压腔初始容积之间存在一定的变化规律，而且这种规律具体参数又将随介质不同而变化[11]。

为了实现装置整个压力范围上适当的脉宽，对装置设计了3种规格的液压活塞系统，其活塞直径分别为5、8和10 mm，同时配备3种不同质量的锤体，质量分别约为10.1、7.8、5.1 kg。为了保证锤体下落的垂直性以及与活塞之间的同轴性，并减小锤体有效作用时所受的摩擦力，落锤装置采用扶正机构与锤体分离。锤体和扶正机构之间使用滚珠轴系以减少摩擦力。落锤装置的主要结构见图2。

采用KISTLER 6213压电式压力传感器对脉冲压力发生器在各种不同锤体与活塞组合时产生的脉冲压力进行测试。当锤体与活塞之间不使用缓冲垫时，在部分锤体与活塞组合中出现压力脉冲波形高频振荡现象，如图3所示。一般密闭腔内压力振荡主要来自2个方面:一方面,来自于快速变化的压力造成压力腔内液体介质谐振，但在本装置中，脉宽都在5 ms以上，压力波的波长远大于压力腔内尺寸，因此并不具备介质谐振的条件；另一方面，活塞本身的振荡会引起压力的振荡，在本装置中，锤体与活塞之间的弹性碰撞(近似完全弹性碰撞)可能造成多次碰撞从而引起活塞的振荡，需要利用碰撞中的塑性能量损失以及锤体与活塞系统的配合加快活塞振荡的衰减，使两者在脉冲压力峰值点之前尽快达到运动同步。通过多种组合的大量实验，并在锤体与活塞之间最终使用活塞直径为8 mm的活塞系统以及质量为10.1、7.8 kg的2个锤体实现了(10～500) MPa的脉冲压力，脉宽都控制在(5～9) ms之间，波形无明显振荡。部分脉冲压力波形如图4所示。

3 脉冲压力激光干涉测量

3.1 测量原理

为了实现脉冲压力的光学测量，必须把光学测量系统得到的运动参数(位移、速度、加速度)转化为压力的变化。利用牛顿第二定律，对锤体和活塞等进行受力分析，来建立力学模型，得到脉冲压力的计算公式。在锤体碰撞活塞的过程中，把锤体m1、活塞杆m2看成一个整体，它们将受到重力(m1+m2)g、惯性力(m1+m2)a、摩擦阻力f、活塞端面液压油压力pS0的作用。忽略锤体、活塞杆中加速度的不一致与分布不均、摩擦阻力等因素，考虑到在工作中，活塞杆的重力一直是加载在介质上的，对不同时刻的动力学分析有：

(1)

式中：S0为活塞面积，p为活塞端面油压力，a为锤体加速度(往上为正)。S0和m1、m2可以通过常规方法比较准确地得到，而加速度a由激光干涉测量系统从顶部测量锤体运动得到。脉冲压力幅值为：

(2)

3.2 误差分析

在建立模型和公式(1)和(2)的过程中，进行了各种简化和假设，这些在实际测试计算中都可能引入测量误差。需要对这些误差源进行分析和补偿。公式(1)和(2)的不完整性主要体现在以下几个方面：

(1)摩擦力f的影响

摩擦力包括锤体与扶正机构间的摩擦力、活塞与套筒间的摩擦力。

锤体与导向轴承之间的摩擦力采用高精度力变送器直接测量。通过测量多个锤体在导向轴承中运动时传感器受到的垂直方向力减去锤体的自重，来评估摩擦力的大小。经过多次测试，1#锤与导向轴承之间的摩擦力6次测量平均值为4.212 N，最大值为4.574 N；2#锤与导向轴承之间的摩擦力6次测量平均值为0.627 N，最大值为1.141 N；3#锤与导向轴承之间的摩擦力6次测量平均值为0.514 N，最大值为0.633 N。

活塞杆与活塞缸之间的摩擦力主要通过活塞杆的自重和配重来评估，通过活塞杆的自重或加上适当的配重，使活塞杆刚好在缸内移动。可以认为，这时活塞杆与活塞缸之间的静摩擦力不超过当时的活塞杆的自重和配重之和。而脉冲压力的峰值点也是活塞杆速度过零点，因此峰值点的摩擦力不超过静摩擦力。对活塞直径为8 mm的活塞系统进行实验，多次实验中活塞杆的自重都已经使活塞在缸内向下滑动，其自重为0.660 N，因此静摩擦力不大于0.660 N。

(2)活塞端面压力与压力传感器真正感受的压力之间的不一致 ∂p

由于常用的液压介质中的声速基本超过1 200 m/s，而脉冲压力的频谱主要集中在较低频率，5 ms脉宽的半正弦信号的频谱基本集中在2 kHz以内。

液压腔内最大尺寸不超过50 mm，考虑不同频率成分的压力波在液体介质中传播时的最大相位偏差，通过不同频率的正弦波按照以上最大相位偏差进行相移后重新合成，与标准的半正弦波进行比较，幅值最大偏差小于0.2%。

由于无法直接测量活塞端面的压力，只能在液压腔进行压力测量，对一个压力腔侧面加工了2个传感器安装孔，对各种不同压力幅值与脉宽、活塞不同位置与方位等状况下的脉冲压力进行了测试，2个传感器的测量结果相对偏差都在0.4%以内。

(3)加速度分布不均的影响

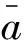
通过有限元法对锤体、缓冲垫和活塞中的加速度分布进行了分析。针对不同质量块及其材料阻尼参数以及不同载荷工况进行建模仿真分析，加速度分布产生的误差都在0.5%以内。同时对锤体上端面的中心与边缘的加速度偏差进行了测试，3只加速度计以L型分布，从测试结果发现，锤体边缘的加速度与锤体中心的加速度存在比较小的偏差，经过多次实验，这种偏差都在1%以内。

另外由于锤体与活塞之间碰撞并不是塑性碰撞，在整个脉冲压力发生过程中两者存在加速度不一致，特别是活塞存在明显振荡时。本装置消除了脉冲压力波形上的明显振荡，说明锤体与活塞在峰值点前已经基本运动同步，即加速度一致，因此对于只关心零点与峰值点的幅值灵敏度校准而言，锤体与活塞之间加速度不一致的影响可以忽略。

因此，完整的数学模型应该是：

(3)

式中：fmax、∂pmax分别为锤体加速度最大点时活塞所受的摩檫力以及压力之间的不一致。

3.3 激光干涉测量实验

利用搭建的脉冲发生装置与激光干涉测量系统进行了脉冲压力激光干涉测量实验。采用外差式激光干涉仪测量锤体上端面中心的速度变化。实验中同步采集压力传感器测量输出与激光干涉测量速度输出，再对速度信号进行微分得到加速度信号，并根据式(3)计算得到激光干涉测量压力信号。图5为峰值226 MPa左右实验中同步采集的压力传感器输出信号与激光干涉测量计算的压力信号。可见激光干涉测量并解算动态压力工作正常，压力波形与压力传感器输出波形基本一致。

4 系统实验与分析

4.1 校准装置与实验

根据以上搭建的脉冲压力发生器与激光干涉测量系统，并搭配相应的数据采集分析系统，构成了激光干涉法液体脉冲压力校准装置，整体实物如图6所示。激光干涉系统置于隔震平台上，活塞系统置于隔震地基上与隔震台相互隔离，以减小落体撞击活塞传递到干涉系统的振动，并通过传递的时间造成脉冲压力信号与干涉系统受到的冲击振动信号之间的时间差，从而避免干涉系统振动对所需要脉冲信号测量的影响。

对一支压电式压力传感器(KISTLER 6213B)进行校准实验，得到传感器的动态灵敏度，并与静态灵敏度(12 pC/MPa)进行比较，如表1所示。单次校准幅值灵敏度与静态灵敏度最大偏差为1.72%，6次重复校准幅值灵敏度的相对标准偏差(relative standard deviation,RSD)最大为0.5%。

表1 压力传感器(KISTLER 6213B)幅值灵敏度校准结果Table 1 Amplitude sensitivity calibration of a pressure sensor (KISTLER 6213B) with pulse pressure

4.2 幅值灵敏度校准不确定度分析

(1)平均加速度引入的不确定度包含加速度峰值激光干涉测量误差和加速度分布不均引入的误差。经过校准，在本装置压力脉宽范围加速度峰值激光干涉测量最大相对误差为0.5%，经过仿真分析和实际测试实验，加速度分布不均最大偏差为1%。

(2)根据3.2节中测试分析结果，使用质量为7.8 kg的重锤对幅值为10 MPa的脉冲压力进行测量时，摩擦力引入的不确定度为:

同样，在7.8 kg/100 MPa、10.1 kg/100 MPa、10.1 kg/500 MPa等测量时摩擦力引入的不确定度依次为0.02%、0.06%、0.02%。

(3)活塞杆有效面积由活塞压力计标准装置测量,根据检定证书,其引入的不确定度为0.01%。

(4)经过3.2节中测试分析结果，压力不一致估计最大为0.4%。

(5)根据检定证书, (1～3 000) Hz范围内数据采集系统电压幅值测量最大示值误差为0.1%，信号分析软件通过数字仿真方法进行评定估计标准测量不确定度为0.2%。

(6)根据4.1节中实验分析结果灵敏度校准最大相对标准偏差为0.5%。

在10 MPa点扩展标准不确定度为：

通过对(10～500) MPa多个压力幅值点的幅值灵敏度校准不确定度分析，扩展不确定度在(1.5～1.8)%(k=2)。

5 总 结

基于激光干涉测量技术的液体脉冲压力标准装置，能够真实复现液体介质压力室内脉冲压力变化的时间历程。它利用计量学的基本量—时间和长度、质量，直接、绝对复现动态压力单位量值，实现动态压力的绝对校准，测量过程符合计量学关于绝对法测量的定义和要求。装置实现的脉冲动态压力的可靠溯源，对于压电式压力传感器等无法静态校准的压力测试系统的灵敏度的可靠校准和推广具有重要意义。装置实现的(10～500) MPa脉冲压力校准能满足大部分大压力范围的幅值灵敏度校准，但并不能完全满足发动机内流压力脉动等中小压力范围以及500 MPa以上超高膛压测试传感器及测量系统的校准需求，因此在脉冲压力的测量范围方面有待进一步扩展。

参考文献：

[1] The Instrumentation, Systems, and Automation Society. A guide for the dynamic calibration of pressure transducers: ISA-37.16.01-2002[R]. 2002.

[2] HJELMGREN J. Dynamic measurement of pressure: A literature survey[R]. 2002:34.

[3] JIM L, DAN C. Dynamic pressure calibration[R]. PCB Piezotronics Technical Note TN-15-0205, 2005.

[4] 孔德仁,孙海波,朱明武,等.压力动态绝对校准方法研究[J].南京理工大学学报,2000,24(3):261-264.

KONG Deren, SUN Haibo, ZHU Mingwu, et al. Dynamic pressure absolute calibration method[J]. Journal of Nanjing University of Science and Technology, 2000,24(3):261-264.

[5] BARTOLI C, BEUG M F, BRUNS T, et al. Traceable dynamic measurement of mechanical quantities: Objectives and first results of this European project[J]. International Journal of Metrology and Quality Engineering, 2013,3(3):127-135.

[6] LAKKA A, SAXHOLM S. Drop-weight system for dynamic pressure calibration[C]∥8th Workshop on Analysis of Dynamic Measurements. Turin, 2014.

[7] DURGUT Y, AKSAHIN E, BAGCI E, et al. Preliminary dynamic pressure measurement system at ume[C]∥XXI IMEKO World Congress. Prague, 2015.

[8] MALENGO A, PENNECCHI F. Drop-weight system for dynamic pressure calibration: Calibration models and methods[C]∥8th Workshop on Analysis of Dynamic Measurements. Turin, 2014.

[9] BRUNS T, FRANKE E, KOBUSCH M. Linking dynamic pressure to static pressure by laser interferometry[J]. Metrologia, 2013,50:580-585.

[10] KOBUSCH M, BRUNS T. European research project for the dynamic measurement of mechanical quantities[J]. PTB Mitteilungen: Amts-und Mitteilungsblatt der Physikalisch-Technischen Bundesanstalt, 2015,125(2):4-11. DOI:10.7795/310.20150202.

[11] 朱明武.压力准静态校准技术[J].宇航计测技术,2004,24(2):19-21.

ZHU Mingwu. Pressure quasi-static calibration technology[J]. Journal of Astronautic Metrology and Measurement, 2004,24(2):19-21.