一种基于差分进化混合粒子群算法的多无人机航迹规划
2018-05-18于鸿达王从庆
于鸿达, 王从庆, 贾 峰, 刘 阳
(南京航空航天大学,南京 211100)
0 引言
多无人机航迹规划是无人机自主执行任务以及顺利完成任务的先决条件之一[1]。因此无人机飞行前,一般会根据其飞行性能、任务和已经获得的威胁信息设计出多条离线飞行航迹[2]。遗传算法[3]、蚁群算法[4]、人工蜂群算法[5]以及粒子群算法[6]等群体智能算法越来越多地应用于多无人机航迹规划问题。文献[7]运用Voronoi图的方法并采用协同策略实现了满足时间约束的多无人机航迹规划;文献[8]分别对两目标决策和三目标决策运用多目标优化算法得到了所需要的结果;文献[9]运用数学方法实现了满足多约束的多无人机航迹规划;文献[10]将NSGA-II算法与Nash Equilibrium方法相结合实现无人机从起始位置到目标位置,再由目标位置到终止位置的航迹规划;文献[11]通过遗传算法得到了多无人机的航迹,并对其进行了平滑处理。
但是目前的多无人机航迹规划都存在一些问题:考虑目标单一、航迹规划约束分析不全面或是最后只生成了二维的航迹规划[12]。所以本文为了解决多无人机航迹规划存在的问题,对航迹空间进行了建模以及对多无人机航迹规划进行了约束分析,同时在航迹规划空间设计和规划了多个航点,并对航点进行了分配,最后使用一种混合粒子群算法完成了多无人机三维航迹规划且进行了仿真验证。
1 地图环境建模
本文中,航迹规划的环境为城市环境,所以采用的地图模型划分为基准地形模型、楼房建筑等障碍区域的建模以及威胁区域3个部分。
基准地形建模时,将飞行区域设为500 m×500 m的直角坐标区域,并且生成随机地表来表达城市环境中的地形起伏。
楼房建筑等障碍区域的建模采用了圆柱形模型,圆柱形模型的数学描述为
(1)
式中:Li(x,y,z)表示第i座建筑;(xi,yi)表示第i座建筑的中心坐标;Ri表示第i座建筑的半径;Zi表示第i座建筑的高度;ε表示建筑物之间的最小安全距离。
对于威胁区域,一般是指电磁干扰区域、禁飞区域以及一些军事探测区域等,本文采用了半球形模型来对威胁区域建模,其数学描述为
(2)
式中:Wi(x,y,z)表示第i个威胁区域;(xi,yi,0)表示第i个威胁区域的中心;ri表示威胁区域半径。
用上述方法对航迹规划空间进行建模,结果如图1所示。
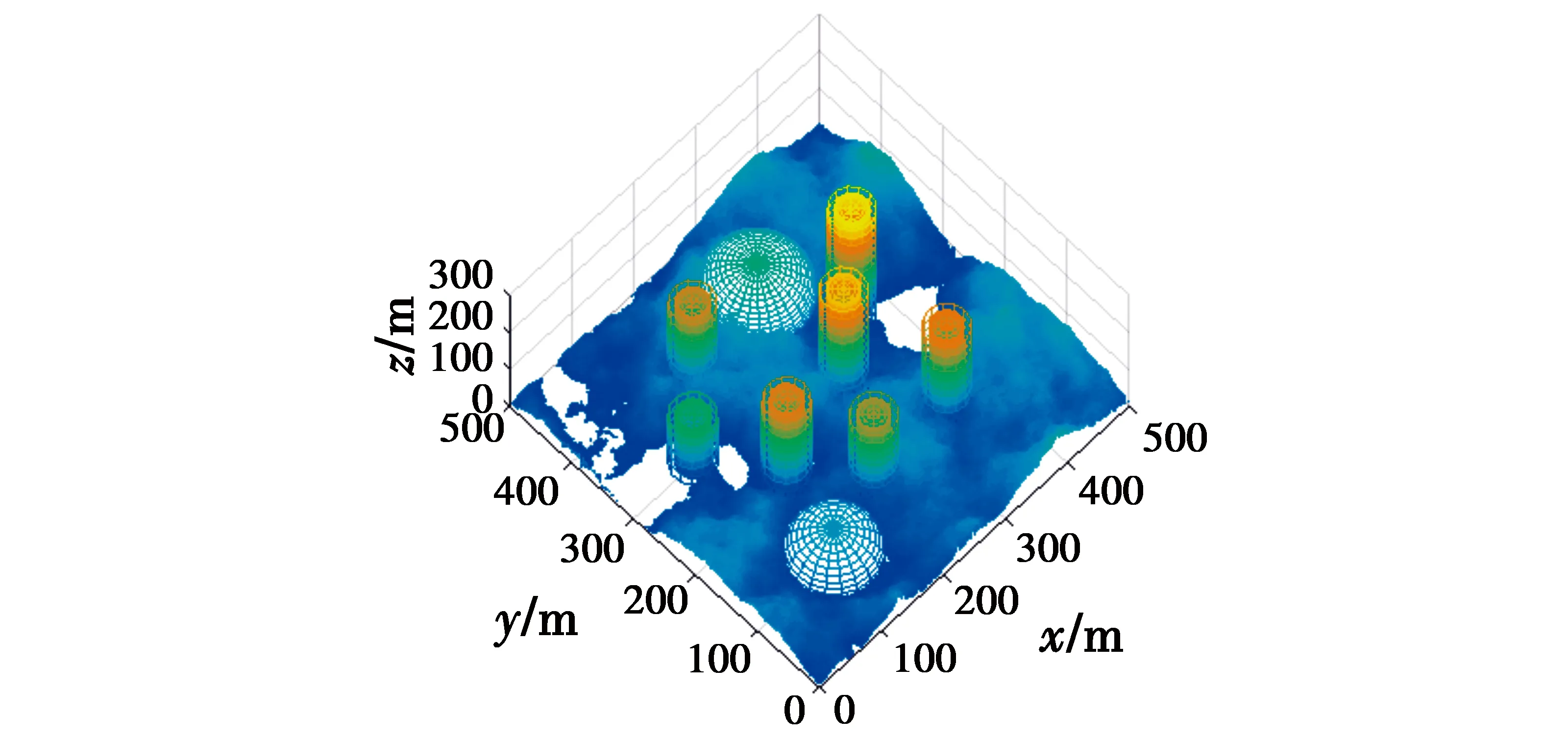
图1 航迹规划空间建模Fig.1 Modeling of path planning space
2 多无人机航迹规划约束分析及代价函数
2.1 子无人机约束分析
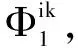

(3)

2) 剩余飞行时间约束。无人机在执行一次任务过程中,其剩余飞行时间也是评价无人机飞往航迹节点Pi的代价因素之一,可以用数学公式表示为

(4)

3) 飞行地形约束。地形约束可以是地理上的不可飞区域、未经允许的禁飞区域以及雷达等电磁干扰威胁区域。
对于楼房建筑类地形约束区域,地形约束可表示为

(5)
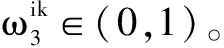
电磁干扰威胁区域约束可以表示为

(6)
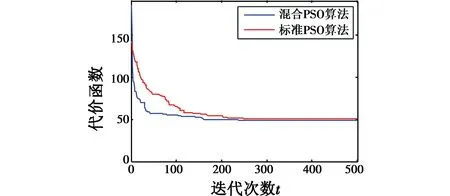
s.t.DkPi 1) 无人机数量约束。多无人机航迹规划需要对多个无人机进行有效分配,实现无人机利用价值的最大化,选取合理的无人机派出数量,同时也不能超出最大无人机使用数量,即 N (7) 式中,Nmax为可用无人机的最大数量。 2) 航迹节点间距约束。无人机执行任务的区域是在某一个确定的范围内,因此,当航迹节点间距过小时,di-dj<ε,就会出现航迹节点冗余的情况,即两个相聚较近的航迹节点中有一个航迹节点是无效的,因此需要对航迹节点间距进行约束,即 Dij∈[Dmin,Dmax] (8) 式中,Dij为第i个节点和第j个节点的间距。 本文中,航迹代价函数的确定是根据航迹节点距离、无人机剩余飞行时间、任务执行效率、环境地形等因素评价的,同时也考虑了多无人机间的约束关系,最终确定飞行航迹。 综上所述,可构造无人机k航迹节点分配后的代价函数为 (9) s.t.N 设航迹节点总数为B,每一个航点代表需要搜索的目的地。多无人机的出发地点与搜索结束后无人机降落地点均相同,分别称为起点Ps与终点Pf。除去起点与终点,应有B-2个航迹节点被N个无人机访问,构造维数为B-3+N的解空间,其解序列可写为 Pi=(Pi1,Pi2,Pi3,…,Pi(B-2),Pi(B-1),…,Pi(B-3+N)) (10) 式中,Pi1,…,Pi(B-2)代表不同的中间航迹节点编号,Pi(B-1),…,Pi(B-3+N)为插入的分割点,用于分割不同无人机将要走过的航迹节点序列。当产生一个可行解时,分割点Pi(B-1),…,Pi(B-3+N)插入Pi1,…,Pi(B-2)中,所以由Pi(B-1),…,Pi(B-3+N)分割出来的N个序列代表了N个不同无人机所要飞行的路线,通过变换分割点在序列中的不同位置与航迹节点序列的排序方式就可改变不同无人机所经过的航迹节点,从而寻找最优路线,简化了无人机群目标搜索规划问题的计算难度。其变换过程如图2所示。 图2 分割点插入航迹节点示意图Fig.2 Inserting of segmentation point into path nodes 假设在D维空间中投放N个粒子,第i个粒子的位置和速度分别为Xi=(xi1,xi2,…,xiD)和Vi=(vi1,vi2,…,viD),该粒子所经历的历史最优位置记作Pi=(pi1,pi2,…,piD),整个种群所经历的最优位置记作G=(g1,g2,…,gD)。 粒子根据下面的公式来更新其速度和位置,即 Vi(t+1)=ω·Vi(t)+c1·r1·(Pi(t)-Xi(t))+ (11) Xi(t+1)=Xi(t)+Vi(t+1) (12) 式中:ω为惯性权重;c1和c2为加速系数;r1和r2为[0,1]之间的随机数;t为当前迭代次数;粒子速度设置限制阈值Vmax,将粒子速度控制在[-Vmax,Vmax]内。 针对PSO算法可能出现早熟现象的问题,通过引入适应度方差来跟踪算法当前的状态。 粒子群适应度方差σ2反映的是种群中全体粒子的离散程度,可以表示为 (13) (14) 为了解决粒子早熟问题,通过引入差分进化操作,对早熟的粒子进行一系列操作来维持群体的多样性,改善算法的全局搜索性能,防止算法陷入局部最优。 对早熟的粒子进行变异操作,即 ui=xr1(t)+F[xr2(t)-xr3(t)] (15) 式中:t为当前迭代次数;xr1,xr2,xr3分别为从粒子种群中选取的互不相同的3个个体;F为缩放比例因子。 在交叉操作中,新的种群Ni由随机矢量Ui和目标矢量Ti共同产生。 (16) 式中:j=1,2,…,D,D为空间维数;Pc∈[0,1],为交叉概率,rand(0,1)为0到1之间的随机数。选择操作采用贪婪策略,即 (17) 式中,fitness为适应度函数,将差分进化操作完成后得到的粒子作为新的粒子,完成了粒子的进化。 惯性权重ω的取值对算法的寻优性能有很大的影响。在迭代初期,一般选用较大的惯性权重来加快算法全局搜索速度,而在迭代后期则取较小的惯性权重来增强局部寻优能力,通过这样的策略可以增强粒子群算法全局搜索与局部最优搜索之间的协调性。所以在原算法的基础上增加自适应调节策略,即 (18) 式中:tmax为最大迭代次数;λ为控制因子。由于式中含有负指数部分,在算法的迭代初期,迭代次数t值较小,惯性权重ω较大,粒子的速度和位置在整个遍历范围内更新;在迭代后期,t值较大,惯性权重ω较小,粒子的速度和位置在小范围内更新,所以该调节策略增强了算法的全局搜索与局部搜索之间的协调性。 通过建立不同航点间代价非对称的航点规划问题,与传统粒子群算法进行对比仿真,来验证上述算法的有效性。设定航点数目为15,航点间间距代价为非对称,无人机个数为3,N=20,tmax=500,ωmax=0.9,ωmin=0.4,λ=20,c1=c2=1.5,Vmax=10,F=0.97,Pc=0.27。实验仿真是在同样实验条件下对同一个航迹规划问题进行10次仿真的平均统计,其代价函数收敛曲线见图3。 图3 混合PSO算法与标准PSO算法对比Fig.3 Comparison of hybrid PSO algorithm with standard PSO algorithm 从图3可以看到,混合PSO算法在第41次迭代就接近收敛,并且最终于第160次迭代时收敛于48.9,而标准PSO算法在第205次迭代时才收敛,最终收敛于50.63。由此能够得出下面结论:混合PSO算法的收敛速度比标准PSO算法更快,航迹代价更小。 本文通过设定航点的方式对多架无人机进行航迹规划。首先在航迹规划空间设定了15个航迹节点并且还有若干建筑物以及威胁区域,设定多无人机航迹规划起点为节点1(20 m,20 m,20 m),经过若干航点,最终都到达终点节点15(450 m,450 m,200 m),航点间间距代价为非对称,对算法的参数进行设置:N=80,tmax=2000,ωmax= 0.9,ωmin=0.4,λ=20,c1=c2=1.5,Vmax=10,F=0.97,Pc=0.27。对无人机设定了飞行约束条件和威胁源,并基于上述混合粒子群算法进行了多无人机多航迹节点的航迹规划,本文分别选择了2架无人机和3架无人机进行了航迹规划。 航迹节点以及障碍物分布如表1所示,节点1为起点,节点15为终点,设定了15个航迹节点,7座建筑物以及2个威胁区域,通过算法仿真最终分别得到如图4和图5所示的2架无人机和3架无人机航迹规划。其中,7个圆柱形区域为楼房建筑障碍物,2个半球形区域为威胁区域,航迹节点在图中1~15处。 表1 航迹节点与障碍物分布表 图4 2架无人机航迹规划图Fig.4 Path planning of two UAVs 图5 3架无人机航迹规划图Fig.5 Path planning of three UAVs 从图4和图5可以看出,两次仿真实验都完成了多架无人机航迹规划,并且成功避开了障碍物以及威胁干扰区域,所以本文混合粒子群算法可以有效地解决多架无人机的航迹规划问题。 本文针对多架无人机的航迹规划问题,通过设定 多个中间节点作为目标点并运用插入分割点的方法来简化寻优过程,通过加入差分进化操作以及自适应调整惯性权重来改进混合粒子群算法,最终实现多无人机航迹规划,验证了算法的有效性并进行了仿真验证。 参 考 文 献 [1] 郑昌文,严平,丁明跃,等.飞行器航迹规划研究现状与趋势[J].宇航学报,2007,28(6):7-12. [2] 孙阳光,丁明跃,周成平,等.基于量子遗传算法的无人飞行器航迹规划[J].宇航学报,2010,31(3):648-654. [3] PEHLIVANOGLU Y V.A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of auto-nomous UAV[J].Aerospace Science and Technology,2012,16(1):47-55. [4] MARTINEZ-ZERON E,ACEVES-FERNANDEZ M A, GORROSTIETA-HURTADO E,et al.Method to improve airborne pollution forecasting by using ant colony optimization and neuro-fuzzy algorithms[J].International Journal of Intelligence Science,2014(4):81-90. [5] 张洛兵,徐流沙,吴梅.基于改进人工蜂群算法的无人机实时航迹规划[J].飞行力学,2015,33(1):38-47. [6] LIN L,GOODRICH M A.Hierarchical heuristic search using a Gaussian mixture model for UAV coverage planning[J].IEEE Transactions on Cybernetics,2017,44(12):2532-2544. [7] MA P B,FAN Z E,JI J.Cooperative control of multi-UAV with time constraint in the threat environment[C]//The IEEE Chinese Guidance,Navigation and Control Confe-rence,2014:2424-2428. [8] AHMED F,DEB K.Multi-objective optimal path planning using elitist non-dominated sorting genetic algorithms[J].Soft Computing,2013,17(7):1283-1299. [9] 白瑞光,孙鑫,陈秋双,等.基于Gauss伪谱法的多UAV协同航迹规划[J].宇航学报,2014,35(9): 1022-1029. [10] LEE D S,PERIAUX J,GONZALEZ L F.UAS Mission Path Planning System (MPPS) using hybrid-game coupled to multi-objective optimizer[J].Journal of Dynamic Systems,Measurement and Control,2010,132(4):1-11. [11] SAHINGOZ O K.Flyable path planning for a multi-UAV system with genetic algorithms and Bezier curves[C]//International Conference on Unmanned Aircraft Systems, IEEE,2013:41-48. [12] 于霜,丁力,吴洪涛.基于改进人工蜂群算法的无人机的航迹规划[J].电光与控制,2017,24(1):19-23.
2.2 多无人机约束分析
2.3 代价函数
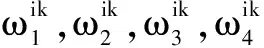
3 航迹规划算法
3.1 航迹节点规划方法

3.2 粒子群算法
c2·r2·(G(t)-Xi(t))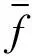
3.3 差分进化操作
3.4 自适应调整策略
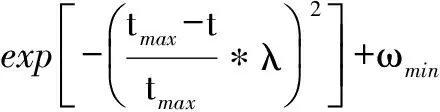
4 仿真实验与分析



5 结束语
