悬臂式掘进机液压系统的可靠性探讨

梁文锋

（大同煤矿集团轩岗煤电有限责任公司梨园河煤矿， 山西 忻州 034114）

引言

悬臂式掘进机是采煤作业中常用的机械设备，它系统构造比较复杂，由机械部件、电气系统、液压系统等组成。地下采煤作业时，作业条件恶劣，存在多粉尘、潮湿、高温等情况，尤其是液压系统常发生故障，占总故障的3/4，需要提升液压系统的可靠性，提升工作效率[1]。

1 悬臂式掘进机液压系统概述

1.1 悬臂式掘进机液压系统的工作原理

悬臂式掘进机根据可根据质量和工作机构切割煤岩的方式不同进行分类。虽然在类型上有所差异，但液压系统的基本组成相近，如图1所示为一般悬臂式掘进机的液压系统构成。

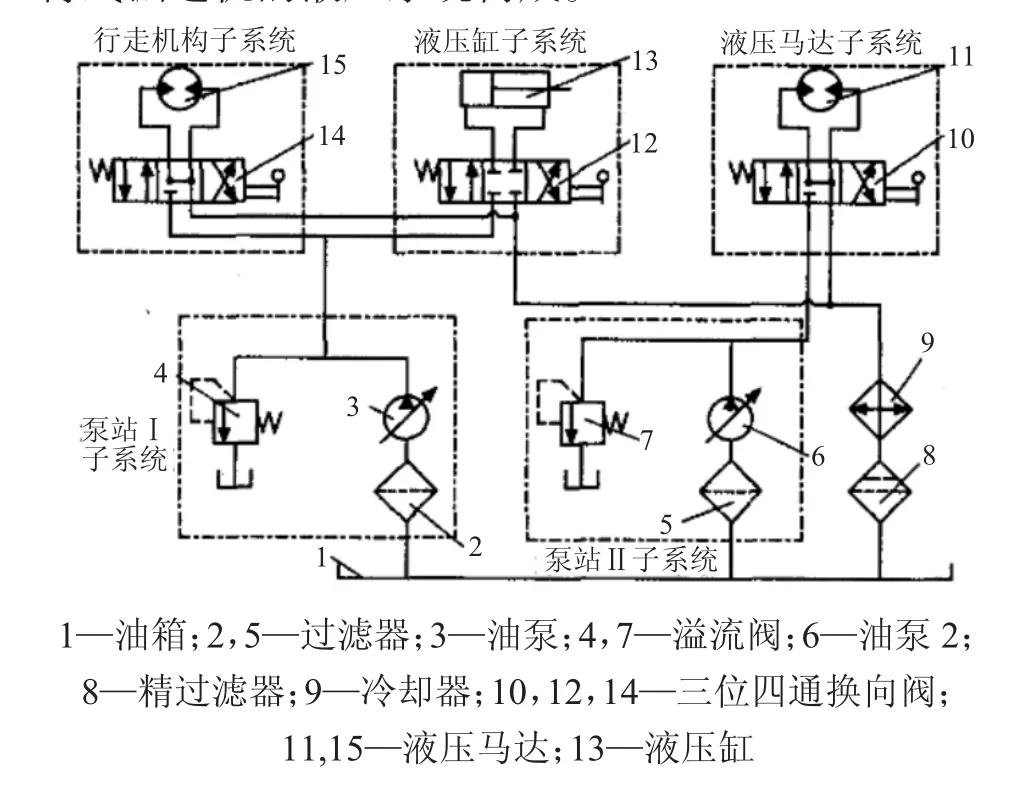
图1 悬臂式掘进机液压系统的构成

液压系统主要由两个动力部组成，分别负责恒功率、压力切断、负载敏感以及恒压力负载敏感。悬臂式掘进机的控制系统依照掘进机的作业方式可分为两大部分。第一部分为单泵控制动力结构，对掘进机的行走部、截割部以及铲板回路、支撑机构进行控制，且不同时作业。第二部分为单泵控制动力结构，对掘进机的装载马达、运输机马达、水泵马达进行控制。这些马达需要同步作业，因此该部分为多负载回路[2]。

1.2 液压系统功能

从悬臂式掘进机的工作情况来看，截割部在工作时的转动由电机进行驱动。除此之外其他各部的工作均由液压系统进行驱动完成作业。因此液压系统的功能可按照控制构建实现掘进机行走、截割机构移动、铲板升降、后支撑升降、履带涨紧、装载、运输、水泵马达带动等。

2 悬臂式掘进机液压系统可靠性模型的基本方法

根据悬臂式掘进机液压系统的构成来看，其属于复杂工作结构。因此要对其展开可靠性研究，需要对复杂系统进行整理和分割，构造可研究性的系统模型，以便于对可靠性的相关参数进行研究。一般可将液压系统按照工作控制原理分割为泵站子系统、行走机构子系统、液压缸子系统以及液压马达子系统。在建立可靠性模型时，其一般步骤为确定液压系统的结构图→转换为可系统靠性框图→确立数学模型→计算可靠性特征量值。最后对可靠性模型进行仿真验证，以确定模型的适应性，找出问题并及时修正[3]。

3 悬臂式掘进机液压系统系统可靠性框图的确定

根据液压系统的工作结构图，将其转换为可行性的系统可靠性框图，其中每一个方框代表液压元件，并采用串并联线连的方式表达各个元件的系统关系。具体建立可靠性框图如图2所示。

4 悬臂式掘进机液压系统可靠性数学模型的确立

图2 液压系统可靠性框图

依据系统的可靠性框图设立可研究的可靠性数学模型。现假设该掘进机的第i个液压元件的可靠性为Ri，失效率为γi，那么就可以获得四个子系统的数学模型。

4.1 泵站子系统的数学模型

根据泵站系统的动力原理，该系统分为泵站ⅠⅡ两个子系统，并构成串联模型。因此两个系统的数学模型相同，可表达为可靠性数学模型：

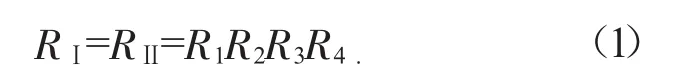
其中：R1—R4依次代表油箱、过滤器、油泵、溢流阀的可靠度。

4.2 行走机构子系统的数学模型

根据行走系统的结构，它由三位四通换向阀和液压马达组成，可构成串联型数学模型，并按照公式（2）进行表述：

其中：R5、R6分别代表行走机构三位四通换向阀以及液压马达的可靠度。

4.3 液压缸子系统的数学模型

液压缸子系统由三位四通换向阀和液压缸组成，二者构成串联结构，故数学模型建立为公式（3）所示情况：

其中：R7、R8分别代表液压缸的三位四通换向阀和液压缸的可靠度。

4.4 液压马达子系统的数学模型

液压马达子系统由三位四通换向阀和液压马达组成，二者构成串联结构，故数学模型建立为公式（4）所示情况：

其中：R9、R10分别代表液压马达的三位四通换向阀和液压马达的可靠度。

5 液压系统可靠度计算

按照系统元件的组成形式，进行可靠度计算。

如果各个系统元件为串联组成，那么假设系统由n个元件组成，则可以对系统的可靠度建立下列关系式：

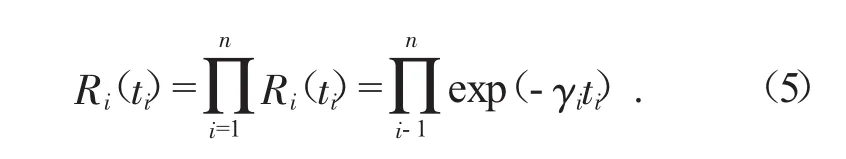
其中：Ri为第i个液压元件的可靠性，γi为失效率，ti为第i各元件的工作时间。

若液压系统的n各元件为并联组成，那么可靠度关系式则可以表达为：

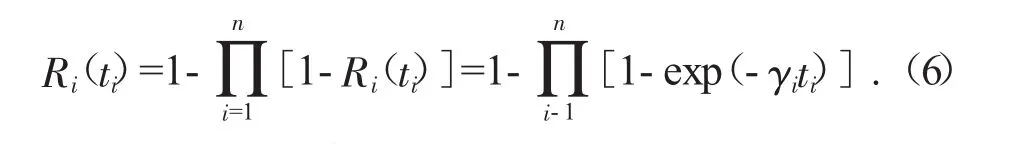
根据本文所描述的系统可靠性框图来看，液压系统属于串并联混合结构，因此将子系统的数学模型进行结合进行分析，可确立总的系统可靠性关系式：

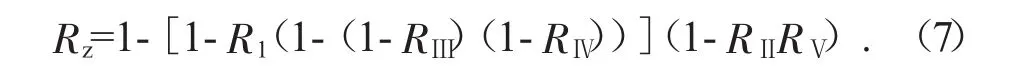
根据统计数据表明液压元件的失效率与时间无关，因此其可靠度与失效率之间呈指数函数模型，可以表达为Ri（ti）=exp（-γiti）。

对已经搜集到的数据进行分析和整理，确定液压元件的基本失效率，如表1所示。

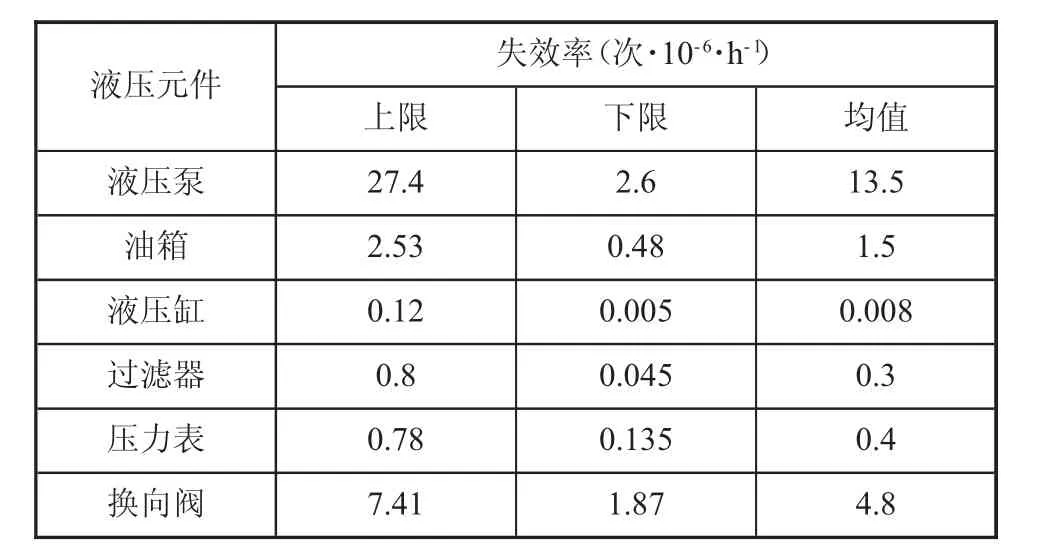
表1 液压元件的基本失效率（部分）

可靠度与失效率之间的函数模型在日常工作中受器件工况的影响和产生差异，因此为了得到准确的失效率，需要确定修正系数，进而可获得失效率的估算公式：

其中，修正系数的数值越大则表明液压系统的工况越恶劣，产生失效的可能性也就越大。按照工况由好到坏分别对修正系数k和工作时间t进行取值，并获得如表2的失效率的统计结果。

表2 不同修正系数下液压系统的可靠度统计（部分）

6 液压系统可靠性模型的仿真分析

为了验证可靠性模型的效果，采用MATLAB软件对悬臂式掘进机液压系统的可靠度进行仿真分析，并获得可靠度随工作时间的变化曲线情况。

根据下页图3显示在修正系数不变的条件下，工作时间越长系统的可靠度越低。那么为了研究修正系数的影响，设定修正系数为20，并同样获得各子系统可靠性变化曲线，如下页图4所示。

根据下页图4仿真结果可以发现在各个子系统中泵站子系统的可靠度最大，液压缸和液压马达子系统的可靠度相近。这是由各子系统的实际工作条件决定的。在所有子系统中，泵站子系统始终提供动力技能，属于长时间工作条件，因此其可靠性最差，需要对其进行优化。马达子系统、液压缸子系统和行走机构子系统之间为全脸结构。行走部的自身并联环节要少于另外两个子系统。因此行走机构的失效率要更高。

图3 液压系统可靠度随时间变化曲线图

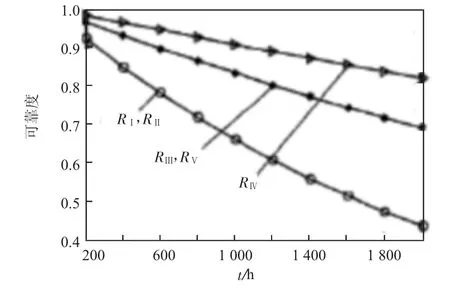
图4 各子系统的可靠度变化曲线

7 结语

悬臂式掘进机的液压系统可靠程度受工况影响，且与各个子系统之间存在逻辑关系。根据发生失效的情况，发现串联环节下失效率更高，应向并联方向进行系统优化，并采取高抗性元件来降低恶劣工况的影响。

参考文献

[1]王琪.悬臂式掘进机的设计与应用[J].煤炭与化工，2017，40（4）：109-111.

[2]于建华.掘进机液压系统的可靠性建模与分析[J].煤矿机械，2015，36（5）：111-113.

[3]费烨，孙波，林闯.EBZ160悬臂式掘进机液压系统设计[J].液压与气动，2015（2）：103-106.