含固体颗粒竖直弯管段塞流/乳沫状流冲蚀速率预测

曹学文, 彭文山,2, 胥 锟, 樊 茵, 李金娟

(1.中国石油大学储运与建筑工程学院,山东青岛 266580; 2.中国船舶重工集团公司第七二五研究所海洋腐蚀与防护重点实验室,山东青岛 266237; 3.惠州兴盛石化仓储有限公司,广东惠州 516000)

在油气开发及集输过程中,段塞流/乳沫状流是常见的流型。段塞流经常出现在起伏管道、海床及近海的采油平台竖直管道中。随着开采时间增长,油井出砂量及原油含水量大大增加,虽然经过过滤,颗粒物仍会存在于油气中,随气、液一起流动。多相流管道内的输送介质为油、气、水、砂多相介质,成分复杂,管内流体的流型多变,砂粒随液体一起流动,出现严重的砂磨管道内壁现象,砂粒经过长时间碰撞管道内壁、弯头、阀门等管道部件,最终对管道系统造成侵蚀破坏,进而造成危险事故[1],导致巨大的经济损失。在番禺35-2海底输气管道系统[2]中以及胜利埕岛油田临海管道均出现砂粒冲蚀导致管道损伤的案例。在含固体颗粒段塞流/乳沫状流中,固体颗粒空间分布随机性大,没有严格规律性,而管道的冲蚀速率及冲蚀最严重位置与固体颗粒的运动及分布有直接关系,要准确预测多相流条件下的冲蚀难度很大。国外部分学者在实验结果的基础上提出经验以及半经验的冲蚀计算公式[3-5],虽然可以计算最大冲蚀速率,但是准确度较差,使用具有很大局限性。国外仅有PARSI等[6]使用Multi-Fluid VOF模型和DPM模型相结合的方法研究了乳沫状流条件下的固体颗粒冲蚀,分析了固体颗粒在管道中的瞬态分布,但是该计算程序耗时巨大,尚有许多问题未研究清楚。Chen 等[7]提出了两种解决段塞流冲蚀速率的计算思路,并且对相关实验工况进行了求解,但文中并未对段塞流的重要参数进行优选,另外这两种求解思路得到的计算结果均与实验值相差较大,准确度不高。笔者在Chen求解思路的基础上,选择最准确参数进行冲蚀计算,提出一种基于段塞体中颗粒分布的冲蚀计算方法,将提出的冲蚀模型计算结果与Chen冲蚀程序计算结果进行对比,验证所提出模型的准确性。

1 模型基本方程

随着入口气体速度增加,段塞流动可转化为乳沫状流。由于乳沫状流流动十分复杂,尚无合理的模型简化该流型,国内外学者在进行流型模型分析时,往往将乳沫状流看做段塞流来处理[8-9],因此进行冲蚀分析时,将乳沫状流按照段塞流模型进行简化分析。段塞流主要由3部分组成:泰勒气泡、泰勒气泡与管壁之间的液膜以及段塞体[10]。段塞流本是一种瞬态流动,在泰勒气泡的前面是平移速度vT、气体段中泰勒气泡速度vC、段塞体速度vS和液膜速度vF,一般来说vT>vC>vS>vF。

段塞单元示意图见图1。

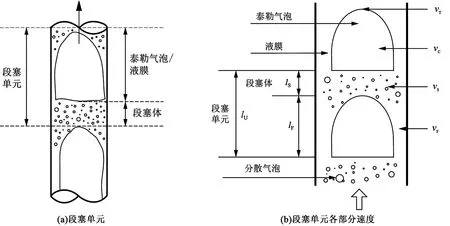
图1 段塞单元示意图Fig.1 Slug unit

连续方程是在以平移速度vT移动的坐标系上推导出来的。对于充分发展的段塞流,根据段塞单元的液相质量守恒,液相连续性方程[11]为

vSLlU=vSHLSlS+vFHLFlF,

其中

vS=vSL+vSG=vm.

(1)

式中,HLF和HLS分别为液膜及段塞体持液率,vSL为液相表观流速,m/s;lU为段塞单元长度,m;lF为膜区长度,m;lS为段塞体长度,m;vS为段塞混合速度,m/s;vSG为气相表观流速,m/s。

段塞长度满足

lU=lS+lF.

(2)

对于段赛单元,根据液量平衡[12]:

(vT-vS)HLS=(vT-vF)HLF.

(3)

同样对于气相,连续性方程为

(1-HLS)(vT-vS)=(1-HLF)(vT-vC).

(4)

其中

段塞长度计算式[11]为

lS=(32cos2β+16sin2β)D.

(5)

式中,D为管径,m;β为管道倾角,(°)。

2 段塞流/乳沫状流冲蚀计算模型

2.1 简化混合流体求解思路(EM1)

在段塞流中固体颗粒可能存在于段塞体、液膜以及泰勒气泡中。Chen等[7]为了求解管道中段塞流/乳沫状流条件下的固体颗粒冲蚀,提出一种简化冲蚀计算方式,假设段塞流/乳沫状流中气液两相简化为二者混合密度和混合黏度的单相流,固体颗粒均匀分布在该单相流体中,同时将简化后单相流体的速度假定为段塞单元速度vT,计算管道内的流体流动情况,进而求解固体颗粒对管道的冲蚀。流体混合密度及混合黏度简化为

(6)

(7)

式中,ρm为简化后单相流体的密度,kg/m3;μm为简化后单相流体的黏度,Pa·s。

2.2 颗粒均布求解思路(EM2)

Chen等[7]的第二种求解思路是假定固体颗粒在液相中均匀分布,并且在充分发展的段塞流中,气泡中并无固体颗粒。假定段塞体中液体夹带率与段塞体中的颗粒含量相同。由于液膜中液体流速较低,假设液膜中的固体颗粒对管道造成的冲蚀相对于液塞中固体颗粒造成的冲蚀极小,可忽略。此时仅考虑段塞体中固体颗粒对管道的冲蚀作用。段塞体中的液体夹带率fe[7]为

(8)

2.3 本文中模型(EM3)

根据Parsi 等[6]的研究结果,在段塞流/乳沫状流中固体颗粒基本上都位于液相之中,即在泰勒气泡中可假定并不存在固体颗粒。这主要是由于泰勒气泡和段塞体之间存在滑移,段塞体能够不断地将泰勒气泡中的固体颗粒捕捉进段塞体中,泰勒气泡中的固体颗粒主要受到惯性力作用。在进行数值计算时,假定固体颗粒全部存在于液相中,即存在于段塞体和液膜中,而在泰勒中并不存在固体颗粒。

气液两相流体总体表现为向上流动,由于气体速度大于液体速度,气泡要突破其前方的液体,但与液体接触的气体速度要与液体速度相同,故气泡中间速度较大,且在两侧靠近液膜的区域,速度方向为向下流动。另外,由于液膜速度较小,固体颗粒的密度较大,液膜中的固体颗粒在重力作用下更易相对气泡向下运动,这就造成了绝大部分液膜中的固体颗粒会相对气泡向下运动而进入液膜下方的段塞体中,造成段塞体中固体颗粒含量较多。提出一种简化方法,假定固体颗粒完全位于段塞体中来求解含固体颗粒段塞流的冲蚀速率,并进一步求得固体颗粒在段塞体以及液膜中的含量。此时,将段塞体假定为具有混合密度及混合黏度的单一流体,混合密度及混合黏度求解方法为

ρm=(1-HLS)ρg+HLSρL,

(9)

μm=(1-HLS)μg+HLSμL.

(10)

3 段塞流参数求解

3.1 段塞平移速度

由式(8)可知,要准确求解段塞体中液体夹带率必需准确获得vT和HLS。国外学者基于大量的实验结果提出众多段塞平移速度模型,Yang等[13]总结文献发现,比较有代表性的模型具有共同的表达形式为

vT=C0vm+vGM.

(11)

式中,C0为滑脱系数;vGM为长气泡的漂移速度,m/s。

由于C0、vm和vGM的计算方法不同,所以上式的形式很多。对国际上比较常用的几个模型进行对比分析,采用准确度最高的模型作为本文计算模型,使用的模型见参考文献[14]～ [21]。

段塞平移速度与段塞含气率αg之间关系式为

(12)

采用段塞流含气率间接验证段塞平移速度模型的准确性,共111组实验数据[22-23]进行验证如图2所示。表1为段塞流含气率误差分析。

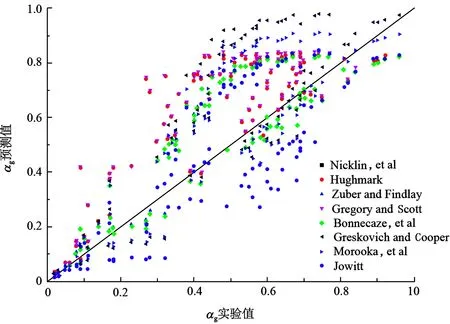
图2 段塞流含气率预测与实验结果对比Fig.2 Comparison of predicted and experimental void fraction of slug flow with different models

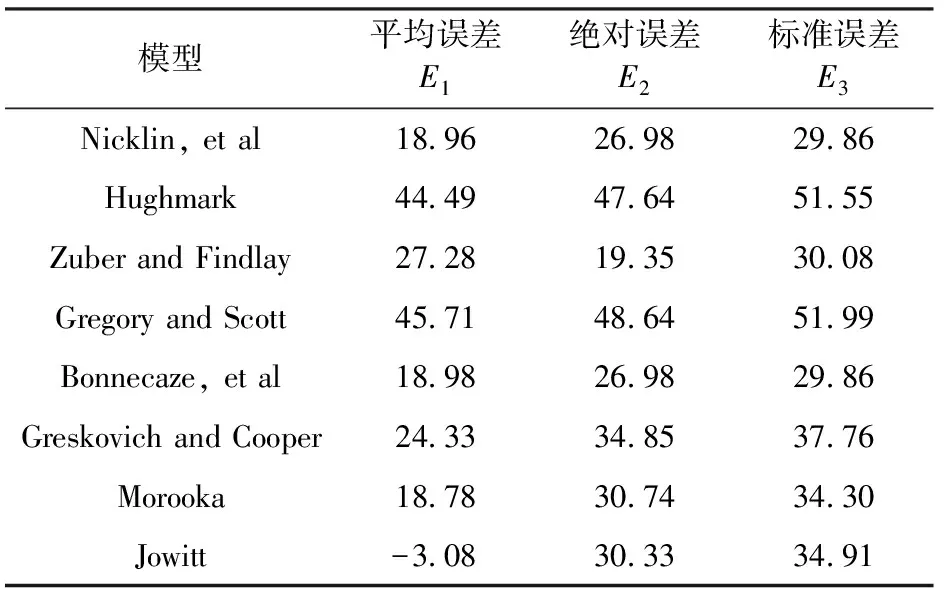
表1 段塞流含气率误差分析Table 1 Statistical results of different models for void fraction prediction of slug flow

表中,平均误差E1、绝对平均误差E2、标准误差E3的计算式分别为

由表1及图2可知,由Nicklin等提出的模型准确度最高,因此使用该模型求解段塞平移速度,其模型形式为

vT=1.2vm+0.35(gD)0.5.

(13)

3.2 段塞体内持液率验证

国外学者对于段塞体内持液率提出不同的求解方法,选用Gregory等[24-27]提出的4个模型以及Abdul-Majeed的实验数据[26]对段塞体持液率模型进行对比分析,选取最准确模型。

表2为段塞体含液率误差分析，图3为段塞体含液率预测与实验结果对比。由图3及表2可以看出,Gregory模型的计算精度最高,因此选择该公式计算段塞体持液率:

(14)

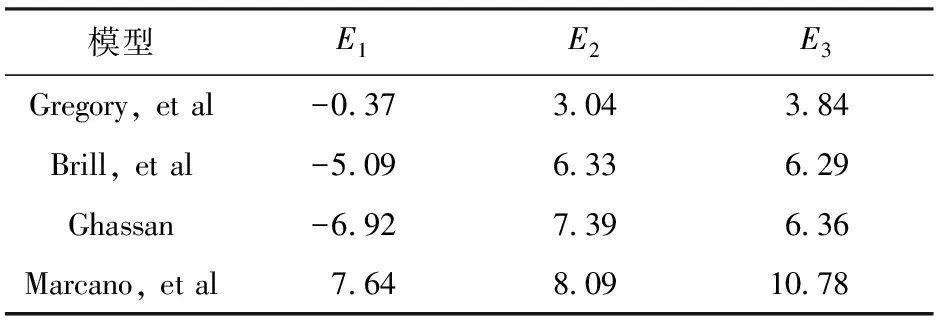
表2 段塞体含液率误差分析Table 2 Statistical results of different models for liquid hold-up prediction of slug body

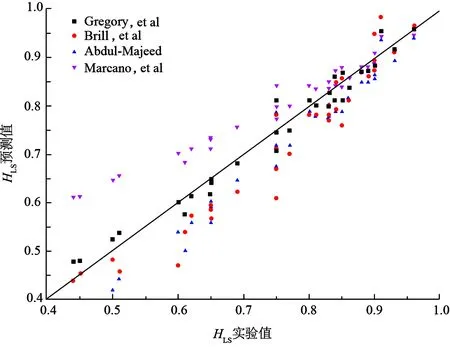
图3 段塞体含液率预测与实验结果对比Fig.3 Comparison of predicted and experimental liquid hold-up of slug body with different models

4 数值模型建立

由于固体颗粒所占体积分数较小,对于固体颗粒采用离散相模型(DPM)进行计算。管道内气液固多相流冲蚀求解分为3步:流场计算、固体颗粒追踪以及冲蚀速率求解。采用Eulerian-Lagrangian 方法在Eulerian 坐标系下求解Navier-Stokes 方程,得到气液两相连续相流场,在Lagrangian坐标系下求解离散相颗粒受力方程,进行颗粒轨迹计算,固体颗粒在简化流体中受到曳力、浮力、附加质量力、压力梯度力,具体受力形式见文献[28]。最终使用冲蚀计算模型提取前两步计算的信息,计算得出管道冲蚀速率。

4.1 管道基本参数

使用FLUENT软件完成相关计算。在计算过程中使用了Kvernvold以及 Birchenough 等的实验数据[29-30],验证提出的冲蚀模型的准确性。选择了8组段塞流数据进行验证计算(表3)。根据Barnea等[31-33]的流型图(图4),所有选择的工况均在段塞流/乳沫状流范围内。为研究气泡流条件下的冲蚀,建立的弯管模型由进口段L1、弯头及出口段L2组成。为使得管道内流动充分发展并考虑到模型计算消耗,取入口段长度为20D,出口段长度为10D。

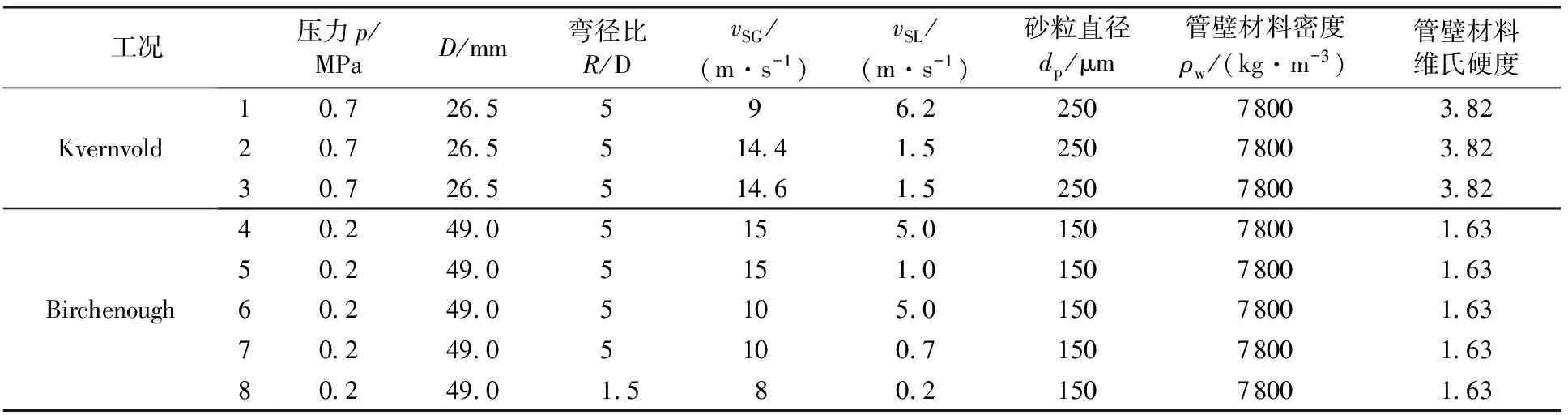
表3 Kvernvold 和 Birchenough等的实验工况

4.2 网格划分

初步计算模型内部为湍流流动,湍流流体质点的不规则运动造成质点在主运动之外还有附加的脉动,因此需要较为精确的网格。网格一共包含两部分:面网格和体网格,由于体网格是在面网格的基础上生成,因此为了保证整个弯管的网格质量,对面网格进行了细化。首先,为了准确获得近壁处的流场分布,在弯管近壁处去网格进行了边界层处理。近壁处的边界层有5层(第一层网格的高度是网格宽度的20%,每层网格增长率为20%)。其他部分采用四边形非结构化网格处理。弯管体网格采用六面体网格划分以提高计算稳定性,减少扩散。

4.3 边界条件

连续相边界设置:由于近壁处存在黏性底层,应用标准壁面函数法近似处理近壁网格区域。入口采用速度进口边界条件,假定流动是充分发展的,出口为自由出流边界。湍流描述中进行湍流强度和水力直径设置。入口处湍流强度可计算为

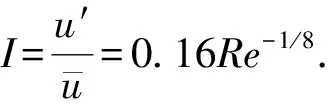
(15)

其中

Re=ρuDH/μ.

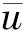
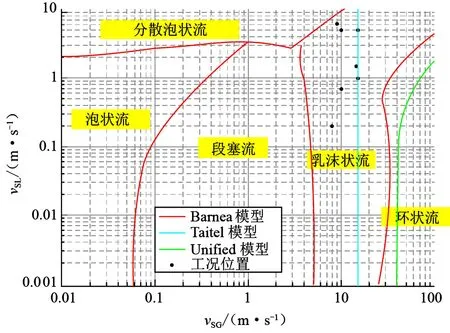
图4 竖直管内流型图及工况位置Fig.4 Flow pattern map for vertical pipe and test points

离散相边界:DPM模型中进口和出口处采用逃逸(escape)条件,壁面采用反弹(reflect)条件,颗粒相的射流采用面射流源,从入口边界射入,颗粒的初始速度与流体进口速度相同。

壁面边界条件:壁面粗糙度常数设为0.5,设定壁面边界为静止壁面,壁面剪切条件为无滑移。固体颗粒与壁面发生碰撞时存在能量转移和能量损失,主要表现在碰撞前后速度分量的变化。为计算碰撞后固体颗粒速度,用壁面设置恢复系数描述颗粒碰撞前后速度变化,采用较为常用的Grant 等[34]提出的随机颗粒-壁面碰撞反弹模型的恢复系数,表示为

(16)

式中,en为法向恢复系数;et为切向恢复系数;α为颗粒冲击角度,rad。

4.4 数值求解

动量、湍动能的离散均采用二阶迎风格式,固体颗粒采用DPM模型,压力速度耦合采用SIMPLE 算法。由于固体颗粒的质量含量很低,计算过程中不考虑固体颗粒对连续相流场的影响,因此采用单向耦合方法求解固体颗粒的冲蚀速率。首先计算得到连续相流动收敛的流场,然后进行颗粒冲蚀求解即可。根据Chen等[35-36]的研究结论,固体颗粒数对于冲蚀速率有较大影响,当固体颗粒数超过20 000个以后,冲蚀速率随固体颗粒数增多基本不变,因此本文中喷射入的固体颗粒数为20 080个,以此排除固体颗粒数对冲蚀的影响。

4.5 冲蚀速率计算

在FLUENT中直接计算出的冲蚀单位为冲蚀速率(kg·m-2·s-1),为了便于同实验结果进行对比,冲蚀速率单位的转换方式为ER(m/kg)=冲蚀量(kg·m-2·s-1)/管壁密度(kg·m-3)/颗粒质量流量(kg·s-1)。

在多相流冲蚀计算中Liu等[20]研究发现, Oka 等[37-38]提出的冲蚀模型其结果可比较准确地预测冲蚀速率。另外,由于Oka， et al模型考虑了较多冲蚀影响因素,如颗粒直径、颗粒参考直径参考碰撞速度和靶材硬度等。相对于其他模型,具有较广的适应范围。在进行数值计算时将Oka等提出的冲蚀模型用用户自定义函数(UDF)导入FLUENT,完成冲蚀计算。

5 结果分析

5.1 网格无关性分析

为了验证网格对计算精度的影响,以工况1为例,对网格进行无关性验证,网格数量为371 280、450 850、615 864、712 287、948 780、1 043 584和1 123 785时,冲蚀速率分别为2.09×10-7、2.06×10-7、2.44×10-7、3.06×10-7、2.68×10-7、2.71×10-7和2.67×10-7m/kg。可见,当网格数量约95万时,随网格数目增多,冲蚀速率不再变化,因此采用该网格进行数值计算,网格划分见图5。

图5 管道计算模型及网格划分Fig.5 Computational geometry and mesh division

5.2 湍流模型验证

由于计算工况的雷诺数较大,流体计算采用标准k-ε湍流模型。标准k-ε模型用于完全为湍流的流场时,可以比较理想地模拟一些复杂的流动,具有较高的计算精度及稳定性。流场求解是管道冲蚀预测流程的第一步,也是冲蚀计算的基础,流场计算的准确性直接影响最终冲蚀结果,因此需对湍流模型进行验证。求解的流场是段塞流/乳沫状流简化成单相流体之后的流场,简化后单相流体密度较大,类似液相流体,因此本文中进行模型验证时,选用Enayet等[39]的液相流场实验数据进行对比验证。Enayet等使用激光多普勒测速仪测量了曲率为2.8D的90°弯头处的流场分布,得到了在雷诺数为43 000湍流情况下弯头30°、60°和75°截面处的流场。图6给出了本文数值计算结果与实验结果的对比(r*=(r-r1)/D)。由图6可知,使用k-ε模型计算弯管的流场分布准确可靠。靠近弯管内壁处的流场变化比外壁处更剧烈,这主要是由于弯头处二次流对流场的剧烈影响造成的。

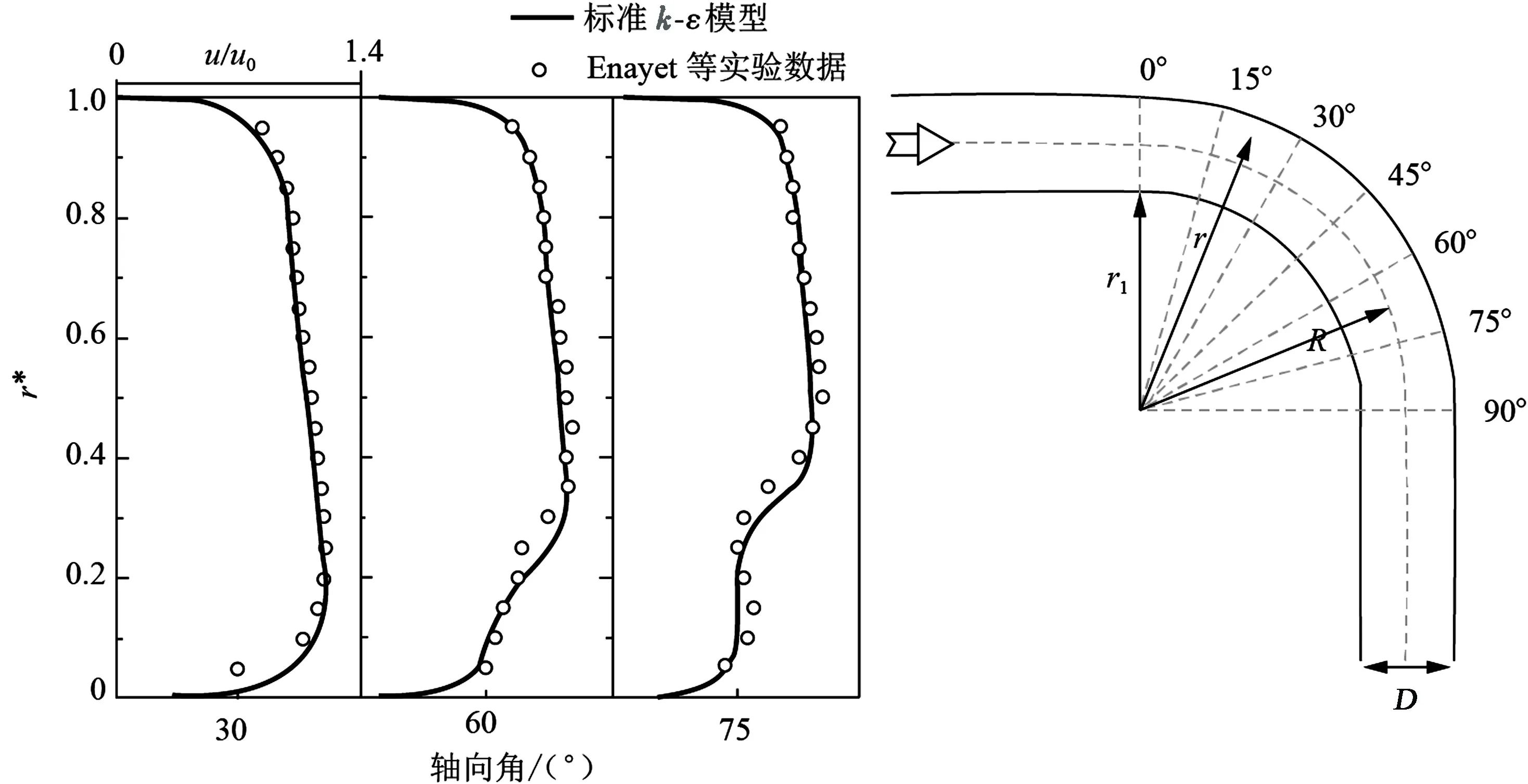
图6 k-ε模型速度计算结果与Enayet等实验结果对比Fig.6 Comparison of predicted velocity profiles with experimental data of Enayet

5.3 冲蚀模型对比

求得3个模型计算所需参数见表4。根据表4相关参数通过数值计算得到冲蚀速率如表5所示。

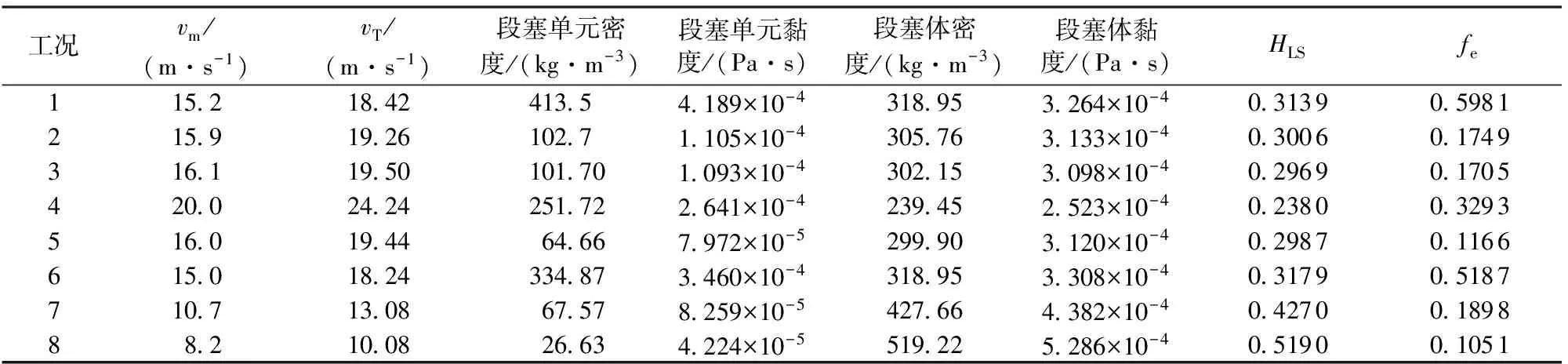
表4 不同工况流体参数及流动参数计算结果

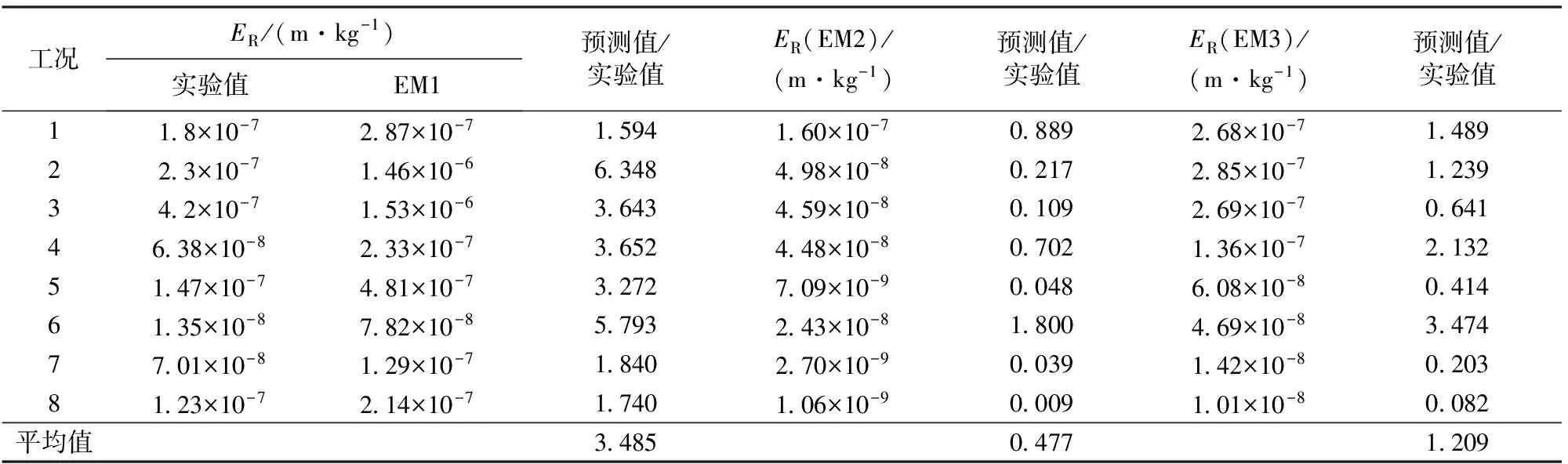
表5 不同模型冲蚀速率计算结果对比

为直观表示数值计算结果与实验结果之间的关系,采用二者的比值进行分析(表5)。由表5可知:EM1模型计算得到的冲蚀速率与实验结果的比值为1.594～6.348。冲蚀速率与实验数据的平均比值为3.485。 而由EM2模型计算的冲蚀速率与实验数据的比值为0.009～1.800,平均值为0.477。而本文EM3模型计算结果为0.082～3.474,平均值为1.209。3个模型误差分析见表6，图7为不同冲蚀模型预测结果与实验结果对比，由表6及图7也可以看出本文模型准确度明显优于其他两种求解思路。

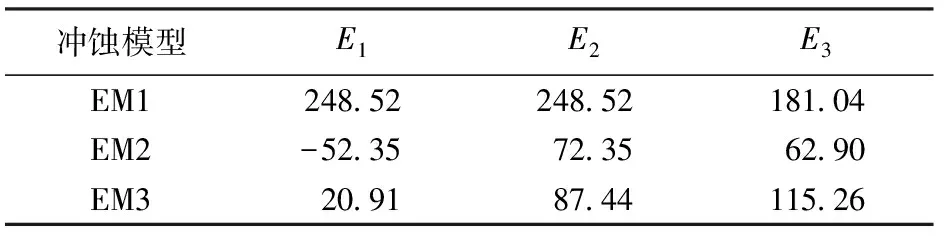
表6 不同预测模型误差分析Table 6 Statistical results of erosion models for experimental data

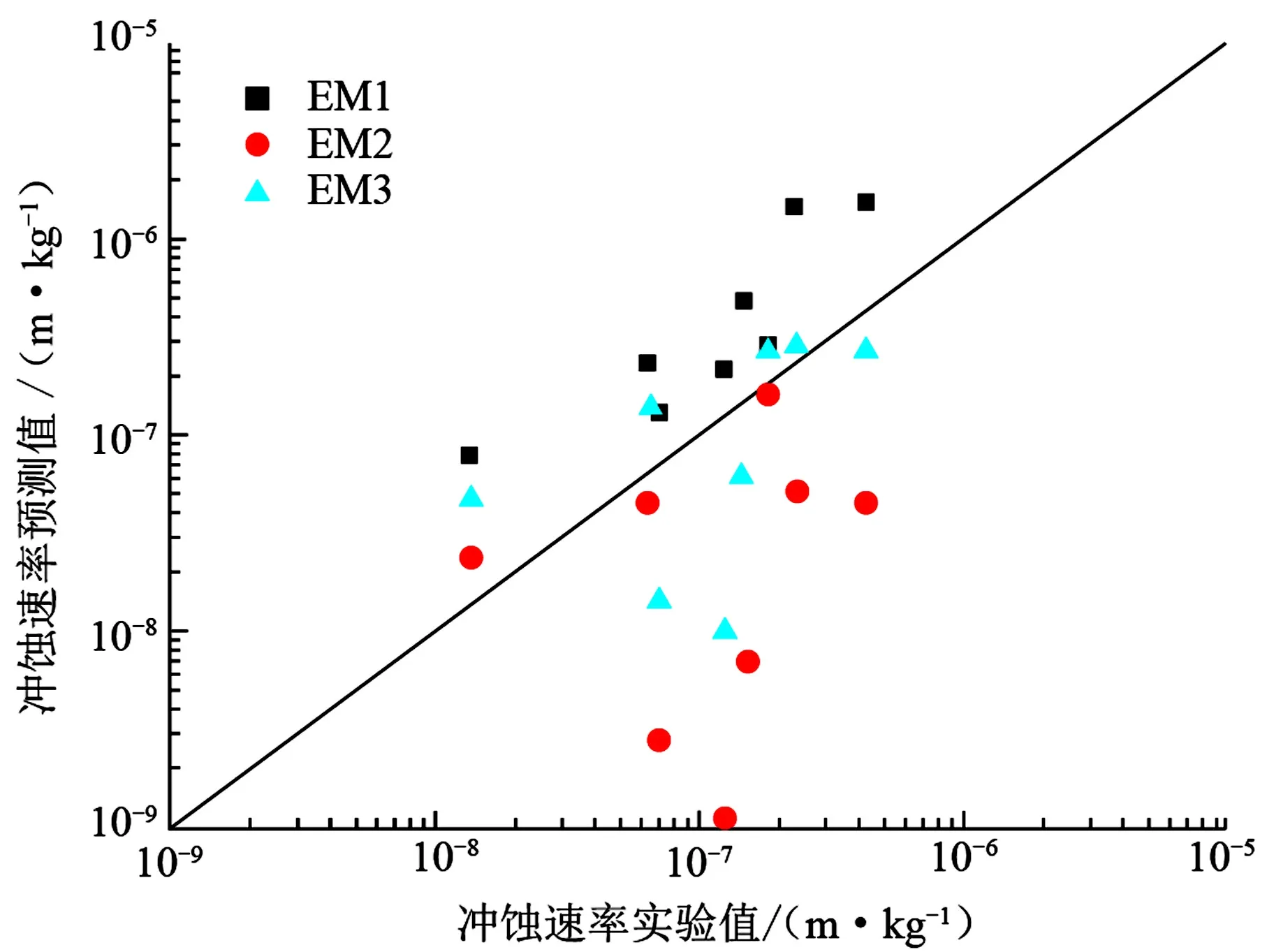
图7 不同冲蚀模型预测结果与实验结果对比Fig.7 Comparison of predicted erosion rate and experimental data with different models

5.4 颗粒分布系数求解

Chen等[7]的研究结果存在较大误差,主要是由于他们认为颗粒在段塞体和液膜中均匀分布,这与管道内颗粒的实际运动情况不符,这主要是由于在段塞流/乳沫状流中气液两相流动极不均匀,液膜与段塞体的运动速度不同,且二者运动过程中与固体颗粒的掺混非常复杂,在段塞体中既不可能包含所有的固体颗粒,同时段塞体与液膜中的固体颗粒也不是均匀分布。由此,基于数值计算结果提出一个段塞体中固体颗粒分布系数λ,对模型计算出的冲蚀速率进行修正,得到考虑了段塞体与液膜中固体颗粒分布不均时的冲蚀速率计算式为

ER=λERsb+(1-λ)ERsf.

(17)

式中，ERsb和ERsf分别为段塞体和液膜的冲蚀速率。

由表6计算可知,基于Oka， et al冲蚀模型计算得到的颗粒分布系数为0.827,即位于段塞体中的固体颗粒含量占所有固体颗粒含量的82.7%。根据表5结果以及分布系数之间关系可知,虽然段塞体中液体夹带率较小,但是段塞体中固体颗粒含量却较大,二者并无密切关联性。

6 结 论

(1)提出的基于段塞体中固体颗粒分布的CFD冲蚀计算模型计算结果与实验值最接近,且与Chen等的简化计算流程相比精确度有较大提高。

(2)竖直管段塞流/乳沫状流中的固体颗粒主要位于段塞体和液膜中,段塞体和液膜中的固体颗粒不是均匀分布,段塞体中的固体颗粒含量较多,固体颗粒在段塞体中的分布系数约为82.7%。虽然段塞体中的液体夹带率较小,但是固体颗粒含量却较多,二者无密切相关性。

参考文献:

[1] 王思邈,刘海笑,张日,等.海底管道沙粒侵蚀的数值模拟及侵蚀公式评价[J].海洋工程,2014,32(1):49-59.

WANG Simiao,LIU Haixiao,ZHANG Ri, et al. Numerical simulations of sand erosion in pipelines and evaluations of solid particle erosion equations[J].The Ocean Engineering, 2014,32(1):49-59.

[2] 钱东良.番禺 35-2 海底输气管道冲蚀规律研究[D]. 成都:西南石油大学, 2015.

QIAN Dongliang. Erosion study on Panyu 35-2 submarine gas pipeline [D]. Chendu:Southwest Petroleum University, 2015.

[3] SALAMA M M. An alternative to API 14E erosional velocity limits for sand-laden fluids[J]. Journal of Energy Resources Technology, 2000,122(2):71-77.

[4] Jr BOURGOYNE A T. Experimental study of erosion in diverter systems due to sand production[R].SPE/IADC 18716, 1989.

[5] MCLAURY B S, SHIRAZI S A. An alternate method to API RP 14E for predicting solids erosion in multiphase flow[J]. Journal of Energy Resources Technology, 2000,122(3):115-122.

[6] PARSI M, AGRAWAL M, SRINIVASAN V, et al. CFD simulation of sand particle erosion in gas-dominant multiphase flow[J]. Journal of Natural Gas Science and Engineering, 2015,27:706-718.

[7] CHEN X, MCLAURY B S, SHIRAZI S A. A comprehensive procedure to estimate erosion in elbows for gas/liquid/sand multiphase flow[J]. Journal of Energy Resources Technology, 2006,128(1):70-78.

[8] ANSARI A M, SYLVESTER N D, SHOHAM O, et al. A comprehensive mechanistic model for upward two-phase flow in wellbores[R].SPE 20630, 1990.

[9] XIAO J J, SHONHAM O, BRILL J P. A comprehensive mechanistic model for two-phase flow in pipelines[R]. SPE 20631,1990.

[10] 王卫阳,陈听宽,罗毓珊.垂直井筒气液段塞流压力梯度的简便算法[J].中国石油大学学报(自然科学版),2006,30(4):75-77.

WANG Weiyang, CHEN Tingkuan, LUO Yushan. A convenient model of pressure gradient calculation of gas-liquid slug flow in vertical wellbore[J]. Journal of China University of Petroleum(Edition of Natural Science), 2006, 30(4):75-77.

[11] 李玉星,冯叔初.油气水多相管流[M].青岛:中国石油大学出版社,2011.

[12] COOK M, BEHNIA M. Slug length prediction in near horizontal gas-liquid intermittent flow[J]. Chemical Engineering Science, 2000,55(11):2009-2018.

[13] YANG S, YU Y, CHEN Z, et al. Evaluation analysis of correlations for predicting the void fraction and slug velocity of slug flow in an inclined narrow rectangular duct[J]. Nuclear Engineering & Design, 2014,273(10):155-164.

[14] NICKLIN D J, WILKES J O, DAVIDSON J F. Two-phase flow in vertical tubes[J]. Trans Inst Chem Eng, 1962,40(1):61-68.

[15] HUGHMARK G A. Holdup and heat transfer in horizontal slug gas-liquid flow[J]. Chemical Engineering Science, 1965,20(12):1007-1010.

[16] ZUBER N, FINDLAY J A. Average volumetric concentration in two-phase flow systems[J]. Journal of Heat Transfer, 1965,87(4):453-468.

[17] GREGORY G A, SCOTT D S. Correlation of liquid slug velocity and frequency in horizontal concurrent gas-liquid slug flow[J]. AIChE Journal, 1969,15(6):933-935.

[18] BONNECAZE R H, ERSKINE W, GRESKOVICH E J. Holdup and pressure drop for two-phase slug flow in inclined pipelines[J]. AIChE Journal, 1971,17(5):1109-1113.

[19] GRESKOVICH E J, COOPER W T. Correlation and prediction of gas-liquid holdups in inclined up flows [J]. AIChE Journal, 1975,21(6):1189-1192.

[20] MOROOKA S, ISHIZUKA T, IIZUKA M, et al. Experimental study on void fraction in a simulated BWR fuel assembly (evaluation of cross-sectional averaged void fraction)[J]. Nuclear Engineering and Design, 1989,114(1):91-98.

[21] CODDINGTON P, MACIAN R. A study of the performance of void fraction correlations used in the context of drift-flux two-phase flow models [J]. Nuclear Engineering and Design, 2002,215(3):199-216.

[22] FEMANDES R C. Experimental and theoretical studies of isothermal upward gas-liquid flows in vertical tubes [D]. Houston, TX:University of Houston, 1981.

[23] SCHMIDT J, GIESBRECHT H, GELD C V D. Phase and velocity distributions in vertically upward high-viscosity two-phase flow [J]. International Journal of Multiphase Flow, 2008,34(4):363-374.

[24] GREGORY G A, NICHOLSON M K, AZIZ K. Correlation of the liquid volume fraction in the slug for horizontal gas-liquid slug flow [J]. International Journal of Multiphase Flow, 1978,4(1):33-39.

[25] BRILL J P, SCHMIDT Z, COBERLY W A, et al. Analysis of two-phase tests in large-diameter flow lines in Prudhoe Bay field [J]. Society of Petroleum Engineers Journal, 1981,21(3):363-378.

[26] ABDUL-MAJEED G H. Liquid slug holdup in horizontal and slightly inclined two-phase slug flow[J]. Journal of Petroleum Science & Engineering, 2000,27(1/2):27-32.

[27] MARCANO R, CHEN X T, SARICA C,et al. Study of slug characteristics for two-phase horizontal flow[J]. Computer Standards & Interfaces, 1999,21(2):118-119.

[28] LIN Z, RUAN X, ZHU Z, et al. Numerical study of solid particle erosion in a cavity with different wall heights[J]. Powder Technology, 2014,254(2):150-159.

[29] MCLAURY B S, SHIRAZI S A, SHADLEY J R, et al. How operating and environmental conditions affect erosion[J]. Corrosion,1999, 34:1-11.

[30] SALAMA M M. An alternative to API 14E erosion velocity limits for sand-laden fluids[J]. Journal of Energy Resources Technology, 2000,122(2):71-77.

[31] BARNEA D. A unified model for predicting flow-pattern transitions for the whole range of pipe inclinations[J]. International Journal of Multiphase Flow, 1987,13(1):1-12.

[32] TAITEL Y, DUCKLER A E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow[J]. AIChE Journal, 1976,22(1):47-55.

[33] ZHANG H Q, WANG Q, SARICA C,et al. Unified model for gas-liquid pipe flow via slug dynamics: part 1: model development[J]. Journal of Energy Resources Technology, 2003,125(4):811-820.

[34] GRANT G, TABAKOFF W. Erosion prediction in turbo machinery resulting from environmental solid particles[J]. Journal of Aircraft, 1975,12(5):471-478.

[35] CHEN X, MCLAURY B S, SHIRAZI S A. Application and experimental validation of a computational fluid dynamics (CFD)-based erosion prediction model in elbows and plugged tees[J]. Computers & Fluids, 2004,33(10):1251-1272.

[36] LIU M, LIU H, ZHANG R. Numerical analyses of the solid particle erosion in elbows for annular flow[J]. Ocean Engineering, 2015,105:186-195.

[37] OKA Y I, OKAMURA K, YOSHIDA T. Practical estimation of erosion damage caused by solid particle impact part 1: effects of impact parameters on a predictive equation[J]. Wear, 2005,259(1):95-101.

[38] OKA Y I, YOSHIDA T. Practical estimation of erosion damage caused by solid particle impact: part 2: mechanical properties of materials directly associated with erosion damage[J]. Wear, 2005,259(1):102-109.

[39] ENAYET M M, GIBSON M M, TAYLOR A, et al. Laser-Doppler measurements of laminar and turbulent flow in a pipe bend[J]. International Journal of Heat and Fluid Flow, 1982,3(4):213-219.