数字凹浮雕生成算法

张兴治，计忠平

（1.杭州电子科技大学计算机学院，杭州 310018；2.杭州电子科技大学图形图像研究所，杭州 310018）

0 引言

浮雕是雕塑与绘画结合的产物，是雕刻的一种，艺术家在一块平板上将他要塑造的形象雕刻出来，用压缩的办法来处理对象，靠透视等因素来表现三维空间。浮雕的材料有石头、木头、象牙和金属等，一般分为浅浮雕、高浮雕和凹雕等。浅浮雕一般是附属在另一平面或曲面上的，因此在建筑上使用更多，用具器皿上也经常可以看到。浮雕在内容、形式和材质上与圆雕一样丰富多彩。浅浮雕压缩大，起伏小，它既保持了一种建筑式的平面性，又具有一定的体量感和起伏感。从古埃及、古希腊和古罗马的神庙和墓碑的雕塑，到中国的庙宇、洞窟和君王的陵墓都有许多浅浮雕艺术。由于其压缩的特性，所占空间较小，所以适用于多种环境的装饰。近年来，它在城市美化环境中占了越来越重要的地位。然而，虽然有大量的3D建模软件以及3D打印技术，浅浮雕的设计却仍然需要依靠艺术家手工制作或使用设计软件如ArtCAM来编辑2D图像来产生3D浮雕效果。而如果直接通过已有的3D模型来构建浮雕将变得更加方便和直观。

近年来，这一课题在计算机图形学领域内受到越来越多的关注。但以往算法主要产生相对基面凸起的浅浮雕，而本文旨在构建数字凹浮雕。凹浮雕在外观上不象普通浅浮雕那样整体高出周围基面，而是相反，陷入周围基面。本文首先从外观以及便于数字化处理的角度对凹浮雕进行如下分类：内凹型以及沉陷型。如图1中所示，内凹型是在平面上雕刻，但是不是雕刻轮廓线，而是“挖”掉形体的表面，使整体呈内凹型；而沉陷型的形体和表面细节与普通浅浮雕类似，但整体沉陷在周围基面或与周围基面持平，这种类型的浮雕一般不常见，但却是古埃及神庙中的典型浮雕。

图1 凹浮雕简单分类

1 相关工作

相对于计算机图形学领域的传统课题，利用三维模型设计数字浅浮雕还是一个相对年轻的研究课题。随着三维模型获取技术的提高以及数字几何处理的发展，近年来有文献研究基于三维场景的数字化浅浮雕设计[1]。Cignoni等人首次将三维场景视为摄像机空间中的高度场，再直接对高度值作非线性缩放，对于离摄像机较近的给予较多的深度范围，最终得到压平后的高度场[2]。这种方法对深度值不复杂的模型和场景能产生较好的浅浮雕，但是对于模型之间由于前后遮挡而形成深度值的不连续而带来瑕疵。Weyrich等人借鉴HDR图像的压缩算法[3]，但并不是直接压缩高度值，而是非线性地改变高度场的梯度值[4]。这样可以改善因深度值不连续而带来的瑕疵。Song等人不直接处理高度场，而是结合网格的微分坐标和特征图来获取高度场[5]。Kerber等人通过双边滤波将高频和低频分离，保留因统一压缩高度场而丢失的细节[6-7]。Sun等人直接处理高度场，并借鉴图像处理中的对比度增强技术并结合梯度域增强特征来产生高质量的浅浮雕，但算法需要的计算量较大[8]。Bian和Hu提出了结合Laplacian坐标和非线性压缩梯度域的保持细节特征的浅浮雕建模方法[9]。Wang等人别出心裁，不是将场景的高度场转化为浅浮雕，而是将场景中提取的“线条”信息转化为雕刻笔画，用以模拟凹线型的雕刻形象[10]。另外，国内学者在此基础上也展开了一些研究[11-14]。

除了从三维场景计算浅浮雕外，近来有一些学者提出从图像转化或手绘等方式产生浅浮雕的方法。Alexa等人在给定光源的前提下由图像计算一个高度场使得其在同样光源条件下得到类似的渲染图[15]，虽然与由三维场景获得的浅浮雕结果比较质量上有差距，但可以作为浅浮雕设计的另一种思路。Li等人则从图像中提取中轴用于构建基本曲面，再结合图像中提取的细节来重建浮雕，该技术旨在模拟砖块和石壁上的浮雕作品[16]。Wu等人提出一种将人脸图像转为浅浮雕的方法，使用神经网络方法由人脸图像计算浮雕图像，再使用Shape-from-Shading技术构建相应的浅浮雕模型[17]，当然该方法局限于人脸图像。Wu等人将二维线型笔划与法线笔划相结合提出一种由单幅图像交互式构建三维曲面（高度场）的方法[18]，虽然该方法侧重于由图像重建三维模型上，但算法也适合于简单浅浮雕的构建。最近，Sykora等人提出类似的方法[19]，但交互方式略有不同，不是指定法线而是手绘图加上表示分块和深度次序的注释。Ji等人分析浅浮雕建模中的关键问题，改变思路，不从高度场着眼，而是从法线角度来思考问题，提出了基于法线图的浅浮雕设计算法[20]。本文工作正是建立在该工作的基础上，通过编辑法线信息来构造凹浮雕。

2 基于法线图的凹浮雕建模

2.1 算法概述

鉴于凹浮雕与普通凸浮雕的区别，本文方法主要解决如何使浮雕表面或轮廓产生凹陷的问题。对于这个问题，从法线角度来处理比从高度场角度直接处理来得更加合理，只需要计算局部的法线以构造凹陷特征，再通过积分计算得到最终的高度场，因此不需要直接处理高度值的不连续问题。本文算法的主要步骤如下：从法线图中抽取轮廓线以及内部重要内陷线条型特征，计算距离图及其法线图；调整基本面的法线信息；再将轮廓线、线条和基本法线合成一整张法线图；最后由合成的法线图重建高度场。

2.2 线型特征提取

（1）轮廓线

为了模拟凹浮雕特别是第三种类型，需要在边缘处构建深凹特征。本文算法首先计算像素到轮廓线的距离图，再根据距离图计算边缘处的法线。图2给出了一个示例。首先计算法线图的轮廓边缘，适当膨胀一下（此例子中向外膨胀6个像素），再计算到轮廓线的欧氏距离图，图2（c）中只显示了轮廓内部的距离图，其中远距离用黄色表示，近距离用暗绿色表示；最后由距离图计算边缘附近的法线值得到轮廓法线图（图2（d））。该例子采用欧氏距离，也可以采用不同的距离函数来塑造不同类型的边缘特征。

图2 边缘轮廓法线图的构建

（2）内部线条

为了塑造凹浮雕中的线条型刻划，本文从图像角度检测出法线图上的凹线条。首先通过边缘检测算子检测法线图的边缘线，但这里有可能存在凸线条，因此再截取Laplace算子的正值抽取出凹线条。该步骤简单高效，通过边缘检测算子的阈值还可以抽取多层次的凹线条。一旦抽取出凹线条，再跟上文中一样，计算距离图，最后由距离图构建相应的法线图。

图3 由凹型边缘线引导的距离图计算法线图

从图3中的例子可以看出，在图3（a）中很多凸线条也被检测出来了，通过Laplace算子将真正凹的线条抽取出来了，再计算到这些点的欧氏距离图，最后由距离图计算法线图。由于采用欧氏距离，没有考虑光滑性，最后得到的法线图有很多尖锐的脊线和谷线，但这里尖锐的谷线正是本文算法所需要的。另外，为了塑造不同的“雕刻痕迹”，可以采用不同的距离计算方法。

2.3 法线调整

由法线图构建浮雕模型的另一个优势就是可以通过调整法线来改变浮雕的整体形状。本文提出两种调整方案，一种是翻转法线，使整体凸起的浮雕变为向内凹陷；另一种则是使浮雕曲面整体倾向于某个方向，本文通过改变法线的x，y分量再单位化来调整法线。

（1）内陷型

对于本身呈整体凸起形状的模型，由翻转法线来构建内凹型浅浮雕是非常直接的，即得到呈整体凹陷的效果。图4中给出了一个例子，通过翻转蚂蚁模型的法线，最终产生了完全内陷的浅浮雕模型。由该例子可见，本文算法可以近似塑造图1中第一种类型的凹浮雕。

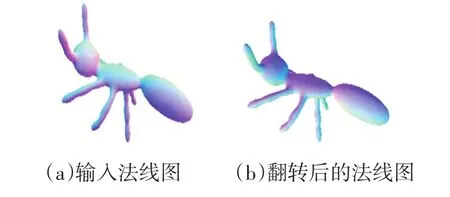
图4 通过翻转法线来塑造内陷型凹浮雕

（2）方向挤压型

为了塑造具有方向性偏倚的效果，可以模拟因长期风化或挤压造成的现象。通过调整法线的方向可以塑造偏向某个方向的效果。本文算法采用如下公式对法线n=（nx,ny,nz）进行方向性调整，其中d是用户设定的一个2维单位向量，用于指示法线偏倚的方向，nxy是法线的x和y分量组成的二维向量。从图5给出了一个示例，其中设定d=[1,0]。可以看出，本文算法通过法线间接地控制高度，用于模仿有些浮雕中的特效。

图5 通过偏转法线来塑造朝某个方向偏倚的效果

2.4 法线合成

由于法线信息和绝对高度值不同，记录的是局部信息，并且具有平移不变性，因此可以将多个法线图组合起来得到一张法线图，再由此计算得到相应的浮雕模型。因此可以将上述几个法线图融合起来生成最终的法线图。本文算法最终处理的是综合原始法线图以及前面步骤中分别产生的轮廓线和内部凹线的法线图。通过积分法线图推导的梯度场得到最终的浮雕模型，该步骤也起到整体光滑的作用，因此本文算法采用简单的方法综合三部分法线图，而并不考虑法线图的光滑性。图6给出了一个例子，该模型对应的一些凹陷特征以凹线的形式呈现出来。另外，也可以对原始法线作不同程度的平滑或竖直矫正，让最终的浮雕呈现出不同的整体平整效果。

图6 合成法线图例子示意图

2.5 浮雕计算

一旦计算得到合成法线图，本文采用文献[20]提出的方法由法线图构建高度场，最后再根据预设的浅浮雕高度值来线性缩放计算得到的高度场。图7给出的例子是由图6中的合成法线图重建出高度场再经线性压缩至一定高度后产生最终的凹型浅浮雕模型。

图7 通过高度场压缩产生浮雕模型

3 实验与讨论

下面将结合实际例子来进一步阐述和验证本文算法。

图8中的例子演示了本文算法构造凹浮雕的过程。由于轮廓边缘法线的存在，使得整个浮雕呈凹陷状，而内部线条呈现了刻划的痕迹。

图8 凹浮雕生成算法实验例子1

图9 中的例子是为了表现不同笔触大小的效果，从图中可以看出，当笔触较小（图9（b））时更趋近于线刻的效果，而较大笔触（图9（c））时凹浮雕的特征更加明显。

图9 凹浮雕生成算法实验例子2

除了以上给出的卡通及人物的模型进行生成凹浮雕以外，本文还提出了其他的类型如汉字来生成凹浮雕。本文首先计算法线图的轮廓边缘，再计算到轮廓线的欧氏距离图，由距离图计算边缘附近的法线值得到轮廓法线图。图10给出的例子也是采用欧氏距离来塑造边缘特征，对原始法线笔触大小等作了不同处理，使汉字产生凹浮雕的效果。

图10 凹浮雕生成算法实验例子3

与文献[20]一样，本文算法以法线图作为处理对象，图11中所示的例子是将文献[20]提出的算法的结果与本文算法的结果作了比较。从该例子可以看出，本文算法生成的结果跟以往算法产生的普通浅浮雕有较大区别。以往算法的一个重要目标是在压缩高度的同时尽量保持原始模型的几何特征，并且尽量保持在垂直视线下的视觉效果。而本文算法产生的浅浮雕压缩高度的同时以内凹的线条呈现原模型的细节特征。而从算法效率上来看，由于主要的计算时间是求解最终的稀疏线性方程组，因此并没较大的区别。

4 结语

本文提出一种由法线图来生成数字凹浮雕的方法。本文从法线图中抽取轮廓线和内部边缘特征，在此基础上计算距离图，再计算距离图的法线，最后将生成的新法线图与原始的法线图混合得到最终的法线图。由法向信息来构建凹浮雕的优势就是，不需要处理深度值的不连续问题。本文方法概念简单，实验表明适合生成各类凹浮雕模型。

目前工作主要研究由法线图如何产生各类凹浮雕模型，但有些问题还值得进一步研究，如：目前凹线笔划的宽度和深度基本一致，研究如何构建宽度和深度自适应的笔划以塑造更加丰富的笔划效果；增加轮廓线和内凹线的随机变化以模拟现实中的浮雕效果；目前在检测凹线时仅仅将法线图作为普通的图像来处理，可以直接从法线信息来计算谷线和脊线，即相当于在物体空间来计算相关特征。

参考文献：

[1]J.Kerber,M.Wang,J.Chang,J.Zhang,A.Belyaev,H.-P.Seidel.Computer Assisted Relief Generation-a S-urvey[J].Computer Graphics Forum,2012,31（8）：2363-2377.

[2]P.Cignoni,C.Montani,R.Scopigno.Computer-assisted Generation of Bas-and High-reliefs[J].Journal of Graphics Tools,1997,2（3）：15-28.

[3]R.Fattal,D.Lischinski,and M.Werman,Gradient Domain High Dynamic Range Compression[J].ACM Tr-nsactions on Graphics,2002,21（3）：249-256.

[4]T.Weyrich,J.Deng,C.Barnes,S.Rusinkiewicz,A.Finkelstein.Digital Bas-relief from 3D Scenes[J].ACM Transactions on Graphics（SIGGRAPH 2007）,2007,26（3）：32-38.

[5]W.Song,A.Belyaev,H.-P.Seidel.Automatic Generation of Basreliefs from 3DShapes[C].In Proc-edings IEEE International Conference on Shape Modeling and Applications.Washington,2007：211-214.

[6]J.Kerber,Digital Art of Bas-Relief Sculpting,Master'Sthesis[C].Univeristy of Saarland,Saarbr¨ucken,Germa-ny,2007.

[7]J.Kerber,A.Tevs,A.Belyaev,R.Zayer,H.-P.Seidel.Feature Sensitive Bas Relief Generation[C].IEEE International Conference on Shape Modeling and Applications.Beijing：2009.

[8]X.Sun,P.L.Rosin,R.R.Martin,F.C.Langbein,Bas-Relief Generation Using Adaptive Histogram[J].IEEE Trans Visualization and Computer Graphics,2009,15（4）：642-653.

[9]Z.Bian,S.-M.Hu.Preserving Detailed Features in Digital Bas-relief Making[J].Computer Aided Geo-metric Design,2011,28（4）：245-256.

[10]M.Wang,J.Kerber,J.Chang,J.J.Zhang.Reliefstylization from 3D Models Using Featured Lines[C].In Proceedings of the 27th Spring Conference on Computer Graphics,2011：63-68.

[11]赵鹏,边哲.曲面浅浮雕生成算法[J].计算机辅助设计与图形学学报,2010，22（7）：1126-1131.

[12]何会珍,杨勋年.曲面浮雕生成[J].计算机辅助设计与图形学学报,2010,22（7）：1132-1137.

[13]周世哲,刘利刚.实时数字浮雕建模[J].计算机辅助设计与图形学学报,2010,22（3）：434-439.

[14]李博,刘胜兰,张丽艳.基于流形调和变换的浅浮雕生成算法[J].计算机辅助设计与图形学报,2012,24（2）：252-261.

[15]M.Alexa,W.Matusik.Reliefs As Images[J].ACM Transactions on Graphics,2010,29（4）：60-66.

[16]Z.Li,S.Wang,J.Yu,and K.-L.Ma,Restoration of Brick and Stone Relief from Single Rubbing Images[J].IEEETransactions on Visualization and Computer Graphic,2012,18（2）：177-187.

[17]J.Wu,R.R.Martin,P.L.Rosin,X.-F.Sun,F.C.Langbein,Y.-K.Lai,A.D.Marshall,Y.-H.Liu.Making Bas-reliefs from Photographs of Human Faces[J].Computer-Aided Design,2013,45（3）：671-682.

[18]T.Wu,C.Tang,M.S.Brown,H.-Y.Shum.S-apePalettes：Interactive Normal Transfer via Sketchi-ng[J].ACM Transactions on Graphics,2007,26（3）：44-48.

[19]D.Sykora,L.Kavan,M.Cadik,O.Jamriska,A.Jaco-son,B.Whited,M.Simmons,andO.-S.Hornung.Ink-and-Ray：Bas-Relief Meshes for Adding Global Illumin-tion Effects to Hand-Drawn Characters[J].ACM Tra-nsaction on Graphics,2014,33（2）：1-15.

[20]Z.-P.Ji,W.-Y.Ma,and X.-F.Sun.Bas-Relief Mo-eling from Normal Images with Intuitive Styles[J].IEEE Transactions on Visualization and Computer Graphics,2014,20（5）：675-685.