基于L1范数特征脸的人脸表情识别算法
2018-05-17马祥李文敏付俊妮
马祥,李文敏,付俊妮
(长安大学 信息工程学院,陕西西安710064)
人脸表情识别就是一种通过计算机对人脸的面部表情信息进行特征提取并分类的方法。大部分现有的表情特征提取方法的目标函数都是基于L2范数[1-7]的,其中L2范数对异常值非常敏感,导致人脸表情识别性能极差。文中提出一种基于L1范数特征脸的人脸表情识别算法,将特征脸与L1范数结合起来进行表情识别。对预处理后的训练样本进行特征提取形成特征脸向量集合,通过L1范数方法对特征脸向量集合分类实现人脸表情识别。在日本JAFEE和美国AR人脸表情数据库上的对比实验结果表明,本文算法对特征空间的选择不挑剔,同时对于特定和非特定人脸表情识别均实现了较满意的识别率。
1 本文算法
1.1 特征脸向量集提取
将所有的训练集人脸表情样本和测试样本都经过预处理后生成w×f的灰度图片,w和f分别表示人脸图像样本的高度和宽度的像素值,然后将其转换为一个G维的列向量[8-11],其中G=w×f。假设人脸表情库中共有M个训练表情样本,则所有训练表情样本可以组合成一个矩阵Z=(z1,z2,…,zM)T,向量zi表示第i个图像构成的一组G维列向量,其中i=1,2,…,M。训练表情样本的“平均脸”X可表示为:

每个测试表情样本与“平均脸”的差值θi表示为:

然后协方差矩阵C表示为:
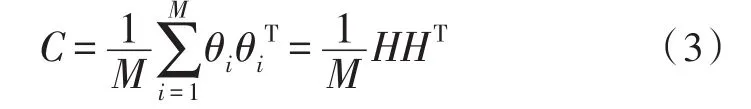
其中,H代表所有测试表情样本与平均脸的差值,即H=(θ1,θ2,…,θM)。为降低计算量,采用奇异值分解定理,通过求解HTH的特征值和特征向量来获得HHT的特征值和特征向量,进而构成特征脸空间[12-15]。HTH的特征值λi和正交归一化的特征向量αi可通过特征值的贡献率计算,1 当求出HTH的特征值λi和正交归一化的特征向量αi后,则协方差矩阵C的特征向量ei表示为: 这里i=1,2,…,o,特征脸空间W表示为: 将每个测试表情样本与“平均脸”的差值θi投影到特征脸空间W,得到特征脸向量集B: 设上节M个训练表情样本的类别属于第l类,这些训练表情样本仍可以组合成一个矩阵,这里,R表示所有表情样本的个数,不失一般性,任何一个与训练表情样本同类的特征脸测试表情样本B往往通过可通过线性组合表示为: 由于特征脸向量集具体所属的类别是未知的,本文假设共有L类的训练表情样本,同理这些所有L类的训练表情样本也可组合成一个矩阵A=[A1,A2,…,AL]∈RG×n,n代表所有L类的特征脸的训练表情样本个数。B可近似的表示为所有训练集样本的线性组合: 这里x表示分类系数向量,若假设x=[0,…,0,xl,1,xl,2,…,xl,n,0,…,0]T∈R,则可知除了与第l类相关的系数不为0外,其他的元素均为0。 由公式(8)得知向量x中的非零元素直接决定了B的所属类别。因此可通过求解线性方程B=Ax来获得系数向量x,由于矩阵A的行数小于列数,则训练字典是过完备的,此时线性方程B=Ax是一个欠定方程,它的解不唯一。根据压缩感知理论[16],如果x足够稀疏,可将求解欠定方程B=Ax的稀疏解问题可以转换为一个求x的L1范数的解的问题: 可知,L1范数的非零解与测试表情样本属于同一个类别。 上述描述都是在理想条件下,然而,现实生活中,人类的表情图像往往都是有噪声存在的,也可能会受到其他因素的干扰,为解决噪声问题,仍需要在B=Ax后面加一个误差项ω,即B=Ax+ω,则转化为求解下面的L1范数问题: 当x获得后,可以根据特征方程δl建立一组新的向量δl(x)∈R,则属于第l类的特征脸的测试表情样本新的近似可表示为: 根据B与的最小残差值(rl)B对应的类别来判断特征脸测试表情样本的所属类别: 为了验证本文算法的可行性,本文在日本JAFFE和美国AR人脸表情数据库上分别进行特定人脸表情识别和非特定人脸表情识别,同时为了更进一步验证本文算法的有效性,在相同的两种表情数据库上采用下采样法与本文算法进行对比。 特定人脸表情识别是指训练样本中允许出现待测试样本的人脸表情图像。本实验在日本JAFFE表情数据库上进行,该数据库中包含了10个个体,213幅日本女性的人脸表情图像,每个个体有7种表情,分别为中性、高兴、悲伤、惊奇、愤怒、厌恶、恐惧。其中每幅图像的人脸均为正面,分辨率均为256×256,如图1(a)所示。文中将原始图像进行预处理,使眼睛在数据库图像中的位置大致相同,脸部尺寸基本一致,随机抽取该人脸表情库中每个人每类表情图像各2-3张共计143张构成表情训练集,其余每个人每类表情各1张共计70张构成测试集。经过预处理后的人脸表情图像如图1(b)所示。 图1 预处理后的部分人脸表情训练图像 从测试集人脸表情图像中随机挑选一人的悲伤表情图像作为测试图像。根据压缩感知理论得到的稀疏系数x为143×1的一个列向量,采用L1范数最小化问题来求解稀疏系数如图2(a)所示。从图中可看出系数中非0元素非常少,且非0元素中的最大值与其他值的差别比较大,最大的系数0.443是第20个系数,恰好对应的是挑选的那个人的表情为悲伤这一类的训练样本。计算测试图像与训练集所有类的残差,结果也显示表情为悲伤的这一类残差值最小。同时本文给出用传统的L2范数求解y=Bx作为对比,相同测试图像的稀疏系数如图2(b)所示,从图可以看出其系数分布比较均匀,各种系数之间的差值也不是很大。所以我们采用L1范数最小化问题来求解稀疏系数进行分类识别。 图2 测试图像在训练集表示的系数 本文取测试表情样本在降维后o为15,即特征向量为15×1,由本文算法得到的各类特定人脸表情识别结果如表1所示。 表1 本文算法的特定人脸表情识别结果(%) 从实验结果可以看出,本文算法对特定人脸表情的正确识别效果良好,平均识别率达到92.03%,其中高兴和惊奇这两类表情的正确识别率达到了99%以上,且没有出现相互误识的情况,这是由于高兴、和惊奇这两类表情在人脸中眼睛、眉毛和嘴巴等敏感区域的相对变化比较明显,所以不容易出现错误识别的情况。而悲伤、中性、恐惧、厌恶和愤怒这五类表情均有个别识别错误,这是由于这几种表情在敏感区域的相对变化不是很明显,所以容易出现错误识别。 使用下采样降维方法提取特征,将图像下采样至8×6,原因在于要保证训练字典的过完备性。下采样降维的各类特定人脸表情识别结果如表2所示。 表2 下采样的特定人脸表情识别结果(%) 从实验结果可以看出,下采样降维方法对特定人脸表情的正确识别效果也不错,平均识别正确率也达到了89.98%。与本文方法提取特征类似,对各类表情的识别结果仍与其在敏感区域的相对变化的明显程度有关,敏感区域变化越明显的表情正确识别率越高。 非特定人脸表情识别是指测试集和训练集没有对应的人物重叠。本实验在AR人脸数据库上进行,其包含了126个个体(70名男性和56名女性),每幅图像的分辨率均为256×256。该数据库中部分不同表情人脸图像如图3所示。 图3 AR数据库中部分不同表情人脸图像 本文选用AR人脸数据库中所有126个个体的其中4种表情:高兴、中性、生气、尖叫共504张人脸表情数据图像,随机挑选100个人的400张人脸表情图像作为训练图像,其余26个人的104张人脸表情图像作为测试集,然后分别对训练集与测试集进行预处理。经过预处理操作后人脸表情图像集分为两种,如图4所示。其中,图4(a)表示预处理后分辨率为64×48的有头发的人脸表情图像集,图4(b)表示分辨率为64×64的去除头发的人脸表情图像集。 图4 经过预处理后部分人脸表情图像 为了尽量减小发型因素对人脸表情识别结果的影响,所以本实验在图像分辨率为64×64的表情库上进行,同理上节所述,本文算法依然与特征数为16×16的下采样法进行对比,具体识别结果分别如表3,表4所示。 表3 本文算法非特定人脸表情识别结果(%) 表4 下采样的非特定人脸表情识别结果(%) 从表3,表4可看出在非特定人脸表情识别中,两者的平均识别率很接近,不过还是本文算法的识别率相对略高。其中对在人脸敏感区域结构的变化比较大的表情仍比较容易识别。而对在人脸敏感区域结构的变化非常细微的表情容易出现相互识别错误的情况。 提出一种基于L1范数特征脸的人脸表情识别算法,将特征脸与L1范数结合起来进行表情识别。在日本JAFEE和美国AR人脸表情数据库上的对比实验结果表明,本文算法对于特定和非特定人脸表情识别均实现了较满意的识别率。 参考文献: [1]Liu M,Shan S,Wang R,et al.Learning expres⁃sionlets on spatio-temporal manifold for dynamic facial expression recognition[C]//IEEE Conference on Computer Vision and Pattern Recognition,2014:1749-1756. [2]Sariyandi E,Gunes H,Cavallaro A.Probabilistic subpixel temporal registration for facial expression analysis[C]//Asian Conference on Computer Vi⁃sion,2014:320-335. [3]Jiang B,Valstar M,Martinez B,et al.A dynamic appearance descriptor approach to facial actions temporal modeling[J].IEEE Transactions on Cybernetics,2014,44(2):161-174. [4]易积政,毛峡,Ishizuka Mitsuru,等.基于特征点矢量与纹理形变能量参数融合的人脸表情识别[J].电子与信息学报,2013,35(10):2403-2410. [5]Jung H,Lee S,Yim J,et al.Joint fine-tuning in deep neural networks for facial expression recogni⁃tion[C]//IEEE International Conference on Comput⁃er Vision(ICCV),2015:2983-2991. [6]刘宁,梁志贞.基于Lp范数的样本对加权的人脸识别[J].计算机工程与设计,2014,35(7):2504-2508. [7]Nojun Kwak.Principal Component Analysis by Lp-Norm Maximization[J].IEEE Transactions on Cybernetics,2014,44(5):594-609. [8]李雅倩,李颖杰,李海滨,等.融合全局与局部多样性特征的人脸表情识别[J].光学学报,2014,34(5):172-178. [9]Gunes H,Schuller B.Categorical and dimensional affect analysis in continuous input:Current trends and future directions[J].Image and Vision Comput⁃ing,2013,31(2):120-136. [10]赵栋杰.改进的LBP算子和稀疏表达分类在人脸表情识别上的应用[J].电子设计工程,2016,24(20):174-177. [11]Li X,Pfister T,Huang X,et al.A spontaneous mi⁃cro facial expression database:Inducement,collec⁃tion and baseline[C]//IEEE International Confer⁃ence and Workshops on Automatic Face and Ges⁃ture Recognition(FG),2013:1-6. [12]Wang Z,Wang S,Ji Q.Capturing complex spatiotemporal relations among facial muscles for facial expression recognition[C]//IEEE Conference on Computer Vision and Pattern Recognition,2013:3422-3429. [13]杨凡,张磊.基于Gabor参数矩阵与改进Adaboost的人脸表情识别[J].计算机应用,2014,34(4):1134-1138. [14]Sariyanidi E,Gunes H,Cavallaro A.Automatic analysis of facial affect:A survey of registration,representation,andrecognition[J].IEEETransactions onPatternAnalysisandMachineIntelligence,2015,37(6):1113-1133. [15]Wang H.Block principal component analysis with L1-norm for image analysis[J].Pattern recognition letters,2012,33(5):537-542. [16]Porter S,ten Brinke L,Wallace B.Secrets and lies:Involuntary leakage in deceptive facial expressions as a function of emotional intensity[J].Journal of Nonverbal Behavior,2012,36(1):23-37.


1.2 L1范数特征脸向量分类
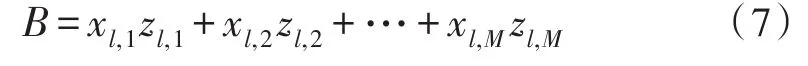


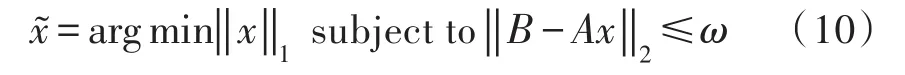

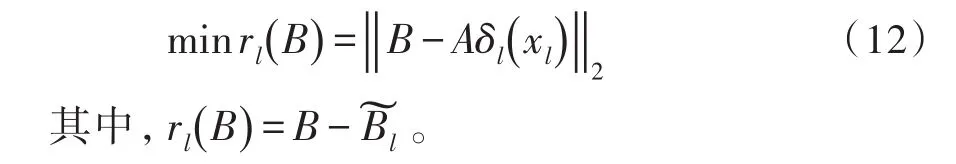
2 实验结果与分析
2.1 特定人脸表情识别

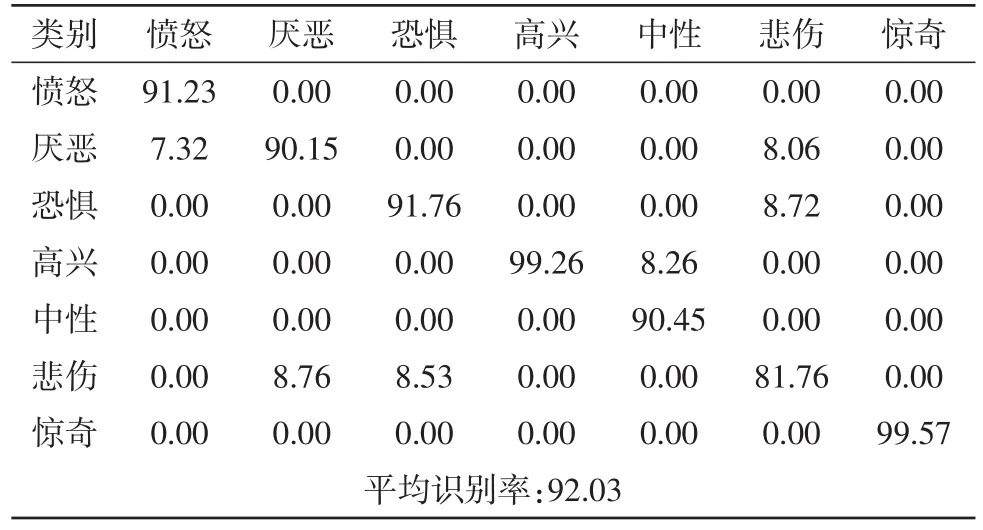
2.1.1 本文算法提取特征的实验结果
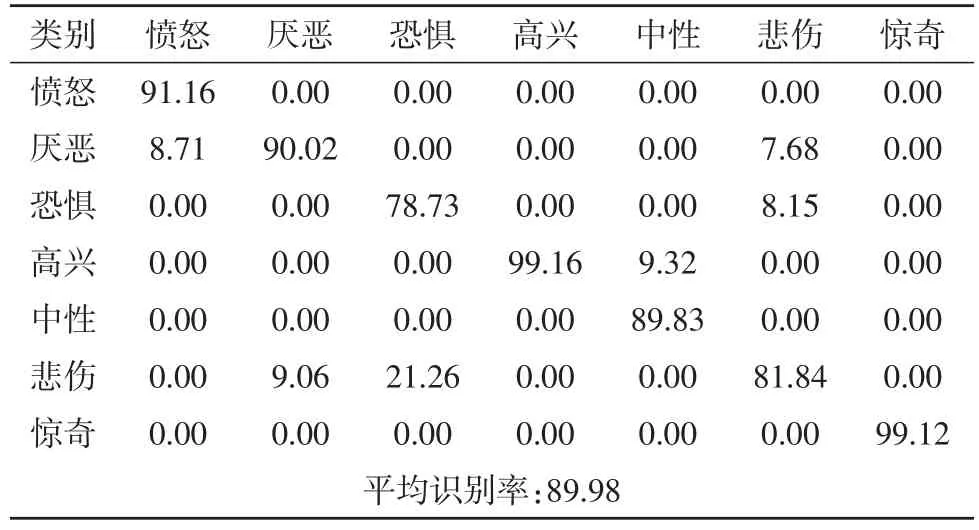
2.1.2 下采样降维方法提取特征的实验结果
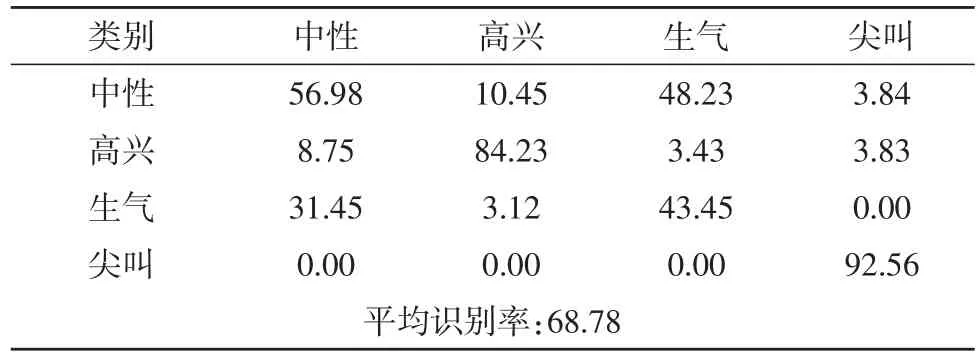
2.2 非特定人脸表情识别



3 结束语
