自适应差分进化算法在光伏组件模型参数辨识中的应用

武 涛， 简献忠， 应怀樵， 郭 强

(1. 上海理工大学 光电与计算机工程学院 教育部及上海市现代光学系统重点实验室， 上海 200093；2. 东方振动和噪声技术研究所， 北京 100084；3.国家卫星气象中心， 北京 100081)

0 引言

近年来，低碳技术在全世界范围内得到迅速发展，太阳能因其丰富、清洁、无污染被认为目前最有前景的可再生能源之一。使得光伏发电得到广泛应用，光伏组件是光伏发电系统中的重要组成部分。因此对光伏组件建立有效模型和获取准确的模型参数对模拟光伏组件实际运行情况和后续的最大功率点跟踪与控制和光伏发电功率预测具有实际意义[1,2]。

近年来，为了描述太阳能电池的输出特性关系，国内外学者对太阳能电池建模做了大量的研究,目前常用单二极管五参数和双二极管七参数等效电路两种模型来描述太阳能电池的I-V特性，主要包括光生电流、反向饱和电流、串联电阻、并联电阻、理想因子等[3-5]。I-V曲线是对太阳能电池的宏观描述，参数模型反映了太阳电池的内部特性，通过对光伏电池参数的辨识可以得到I-V的关系[4，5]。准确的I-V曲线对光伏发电的功率预测和光伏系统仿真具有实际意义[4,6,7]。光伏发电系统中光伏组件主要是由多个太阳能电池单元串联并联组成[1]。在光伏发电和系统仿真中，首先要准确确定太阳能电池模型的参数，才能准确地描述光伏阵列的I-V关系。目前对太阳能电池模型参数辨识主要有3类方法：数学分析近似求解[6-8]、大量数据拟合[10]、智能优化算法[2,12,13,17,18,19]。数学分析近似求解主要依靠数学推导忽略一些小量或者找到一些关键点(如开路电压、短路电流、最大功率点等)进行计算求解，但是存在求解参数不精确误差大的缺点[7,9]。数据拟合在实验数据足够多的情况下才能获得准确的参数，计算量大且费时[11]。基于全局寻优的智能优化算法可以在少量的实验数据的基础上对模型参数进行全局寻优操作，具有计算速度快，求解参数精度高误差小等优点[2,3,12,13]。

根据常用模型参数辨识方法的优缺点,本文提出基于智能优化算法的光伏组件参数辨识。研究发现：在模型参数辨识方面，粒子群优化算法具有实现容易，参数调整少的优点，局部最优解过早收敛粒子飞行速度设置依照经验值的缺点[2,5,16]；蜂群算法具有多角色分工，协同工作机制，稳健性好等优点，蜂群算法的参数设置对算法性能影响明显，参数值由实验获得的经验值确定，缺乏理论依据，容易陷入局部最优解等缺点[2,14,15,16]；遗传算法具有快速寻找最优解的优点和缺乏全局搜索能力和局部最优解过早收敛的缺点[12,14]。因此针对文献[4]参数辨识精度低的缺点和光伏组件模型的非线性和复杂性。本文提出自适应差分进化算法(Adaptive Differential Evolution Algorithm，ADE)，首先对单二极管五参数和双二极管七参数模型进行辨识，然后对基于太阳能电池单元模型推出的光伏组件模型进行参数辨识。将实验结果与模式搜索算法(PS)[4，14]、遗传算法(GA)[12]、粒子群算法(POS)[4]、Newton[4，11]进行比较。实验结果表明，ADE算法辨识结果比文献[4]的辨识精度更高，全局收敛能力更好，使太阳能电池组件电流电压关系更加准确可靠，为光伏发电系统最大功率点跟踪控制和光伏功率预测以及光伏系统仿真提供依据。

1 太阳能电池模型

目前单二极管和双二极管两种模型得到广泛的应用。本文分主要介绍常用的单二极管五参数和双二极管七参数模型和在此基础上发展的光伏组件模型。

1.1 双二极管模型

太阳能电池单元可以被理想的看作一个电流源和一个二极管的并联，然而，实际上由于半导体杂质和非理想性，电流源需并联一个模拟空间电荷电流的二极管，同时考虑电池边缘附近的部分短路电流，电流源并联一个电阻。另外太阳能电池金属触点和半导体材料体电阻由一个串联电阻表示。因此太阳能电池双二极管模型等效电路如图1所示。

图1 双二极管等效电路

在双二极管模型中IL是单元输出电流，Iph为光生电流，Ish为并联电阻电流。Rs和Rsh分别为串联电阻和并联电阻，ISD1和ISD2分别为扩散电流和饱和电流，q是电子的电荷量(1.6e-19 C),K是玻尔兹曼常数(1.38e-23 J/K)，n1和n2为二极管理想因子，T是开尔文绝对温度。太阳能电池二极管七参数模型如式(1)所示：

(1)

式中：Rs,Rsh,Iph,ISD1,ISD2,n1,n2是模型要辨识的参数。

1.2 单二极管模型

在双二极管模型的基础上，认为扩散电流和复合电流虽然是线性不相关的，但是在引入二极管理想因子n时,通常将两种电流组合在一起。单二极管模型等效电路如图2所示，单二极管五参数模型如式(2)所示:

(2)

单二极管等效电路中Rs，Rsh，Iph，ISD，n是要辨识的参数。

图2 单二极管等效电路

1.3 光伏组件模型

光伏组件是由若干太阳能电池单元通过串联并联组成，其等效电路如图3所示。

图3 光伏组件模型

太阳能单元支路串联一个二极管，防止不同支路输出电流不同，电流回流烧毁支路。同时每个太阳能电池单元并联一个二极管，为遮荫区域光伏电流分流，也防止电池在最大短路电流下承受过大负压而损坏。其等效模型如式(3)所示：

(3)

式中：Ns为每条支路的串联太阳能电池单元数；Np为光伏组件并联支路数。为了便于对未知参数求解，对(3)式进行变形得到齐次式(4)，根据每组测量的电压电流值代入到式(4)中得到每组的f值，采用均方根误差(RMSE)和绝对误差(IAE)作为评价指标。

f(VLi,ILi,X)=

(4)

(5)

(6)

式中：X为要辨识的参数向量；N为测量的次数；VLi,ILi为第i次测量的电压电流值。根据评价指标希望参数对任意一组测量值评价指标是最小的。

2 自适应差分进化算法

差分进化算法是一种基于群体差异的启发式随机并行搜索算法，以其易用性，稳健性和强大的全局搜索能力在多个领域得到广泛应用。差分进化算法相对于遗传算法、粒子群算法等智能优化算法尤其擅长多变量函数全局寻优，且收敛速度快。因此针对模型非线性复杂性和多参数情况，选用差分进化算法效果更好[20,21]。

算法原理如下：ADE算法由NP(种群规模)个D(决策变量)维参数矢量xij(i=1,2，…，NP;j=1,2，…，D)，在搜索空间进行并行直接搜索。进化过程中每一个个体进行目标矢量一次，初始种群在搜索空间随机生成的，且初始种群覆盖整个搜索空间。具体算法流程如下：

步骤1：初始化种群大小Np=30,初始收缩因子F0=0.5，交叉概率CRmax=0.9,CRmin=0.5。个体按式(7)产生：

(7)

式中：xi(0)表示第0代第i个个体；xj,i(0)表示第0代第i个个体第j个基因。

步骤2：随机选取种群中的两个不同个体，将其向量差缩放后，与待变异个体进行矢量合成。如式(8)：

Vi(g+1)=xr1(g)+F·(xr2(g)-xr3(g)),

i≠r1≠r2≠r3

(8)

步骤3：对第g代种群{xi(g)}及其变异的中间体{Vi(g+1)}进行个体间的交叉操作，如下式：

(9)

式中：CR为交叉概率；jrand为[1,2，…，D]的随机整数。为了增加适应度好的解进入下一代的机会，设计了自适应调节的交叉概率，

(10)

步骤4：按式4计算个体适应度值，ADE算法采用贪婪算法来选择进入下一代种群的个体，如式(11)：

xi(g+1)=

(11)

步骤5: 判断是否满足迭代次数，若满足输出此时的最优个体即最优解，否者返回步骤2。

3 太阳能电池模型参数辨识

在MATLAB2016b环境下，本文通过ADE算法首先对太阳能电池单元单/双二极管的参数辨识，选两种模型中与实际测量数据拟合较好的模型作为光伏组件模型的基础。然后通过ADE算法对光伏组件进行参数辨识。实验中，太阳能电池单元光生电流与光照强度有关，为了便于与参考文献[4]比较，本文采用Photowatt-PWP201光伏组件，组件由36个电池单元串联组成，标准情况下开路电压为17.49 V，短路电流为0.95 A。工作在温度 45 ℃、光照强度1 000 W/m2环境下(环境一)。同时增加温度35 ℃、光照强度800 W/m2(环境二)，温度20 ℃、光照强度400 W/m2(环境三)两种工作环境验证本文所提出的方法对光伏组件不同工作环境下的有效性和准确性。

模型辨识结果评价如下：本文采用ADE算法，对单/双二极管模型进行参数辨识，收敛结果如图4(a)单,(b)双所示，RMSE分别为2.019e-7和2.121e-7。辨识参数如表1，辨识好参数后为求得计算电流值，对单二极管模型进行处理，具体如下式(12)(13)所示，其中式(12)中全为常数，然后用MATLAB编程通过式(13)解出计算电流It。把辨识参数代入模型中，通过MATLAB编程求得的电流值与实际测量值进行拟合，式(14)是拟合相对误差，单/双二极管电流电压关系拟合相对误差分别为2.467e-4和5.8342e-3。

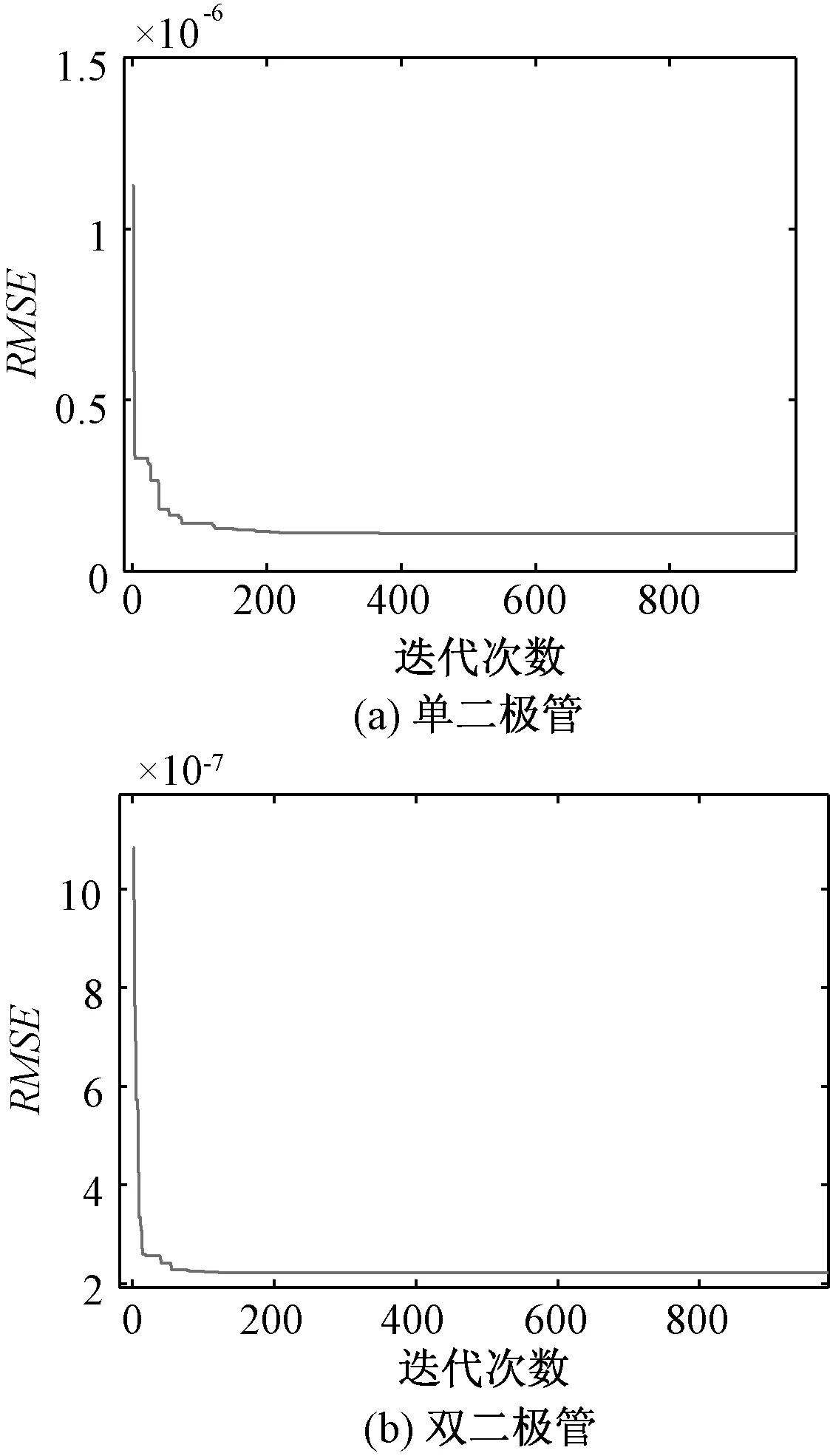
图4 收敛曲线

PSGASAADERs/Ω0.03130.02990.03450.0327Rsh/Ω64.102642.37343.103457.9603Iph/A0.76170.76190.76200.7635Isd/μA0.98800.80870.47980.4315n1.6001.57511.51721.5381RMSE0.28630.01910.0102.019e-7

(12)

It+B+DIt+Aexp(CIt)=0

(13)

(14)

由拟合图5和拟合相对误差得出单二极管模型对太阳能电池单元的电气特性描述更加准确，因此，本文选择太阳能电池单元的单二极管模型作为光伏组件的模型基础，然后通过ADE算法对光伏组件模型参数进行辨识，并对辨识的结果进行评价。

图5 单/双二极管拟合曲线

通过ADE算法对光伏组件模型进行参数辨识，图6是辨识收敛曲线，RMSE为1.402e-2，辨识参数如表2所示(环境一)。把辨识后的参数代入模型求得组件预测电流值如表3所示，计算出总的IEA为0.050 716，与其他几种算法相比均有明显减少。组件电流电压关系拟合相对误差rr为5.73e-4。由评价指标和表3对比结果可以看出，ADE算法对组件模型参数辨识准确，全局收敛能力强，图7中温度35 ℃、光照强度800 W/m2，温度 20 ℃、光照强度200 W/m2两种工作环境下拟合效果基本重合，这两种情况下电流电压关系拟合相对误差分别为4.37e-4和5.16e-4，从而验证了本文所提算法对光伏组件不同工作环境下都能准确有效地辨识出模型参数，这为后期通过硬件结合本文提出的算法对光伏电厂实时监测，辨识不同工作下的模型参数进行实时最大功率点跟踪与控制提供依据。

图6 组件收敛曲线

PSGANewtonADERs/Ω1.20531.19681.20571.3014Rsh/Ω714.2857554.3561555.5556853.9585Iph/A1.03131.04411.03181.0316ISD/μA3.17563.07603.27853.2540n48.288948.586248.450048.3169RMSE0.01180.05370.75060.01402

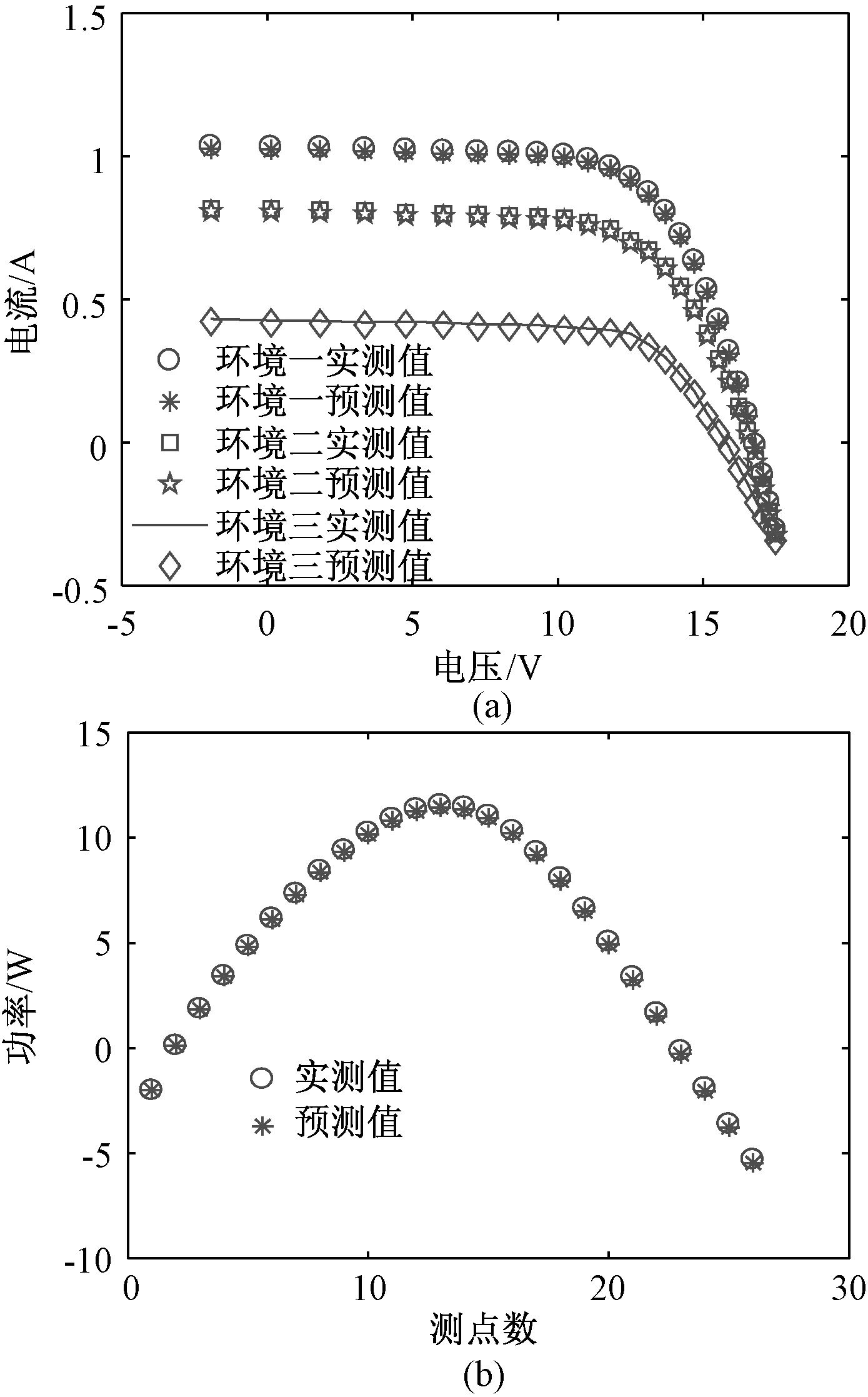
图7 组件拟合曲线

It/APS/IEAGA/IEANewton/IEAADE/IEA1.03150.002130.01019370.0021970.0019691.03000.003030.00869840.0037830.003041.02600.001260.00991150.0026510.0003741.02200.000550.0112280.0014060.0010841.01800.002260.01245760.0002360.0010351.01550.0019860.0117283940.0010090.0003951.01400.0004190.0088803270.0038790.0014571.01000.0025280.0063272390.0064210.0019320.98800.006600.0013330.0112580.0050310.96300.0064990.0009774680.0114490.0068170.92550.0054370.0016079550.0105860.0057020.87250.002350.0043221280.0075650.002070.80750.0023080.004074900.0074220.0027010.72650.0001190.0063036960.0047070.0002030.63450.0012550.0073223380.0030930.0009860.53450.0006170.006625650.0030740.0007240.42750.0011540.0071218650.001730.0012610.31850.000390.00553530.0023410.000420.20850.0016150.004232310.0025740.0017090.10100.0052050.0005253210.0050520.004957-0.00800.0005610.0049515480.0006690.000649-0.11100.0000510.00520440.0022830.000076-0.20900.0002440.0047011460.0031850.000214-0.3030.002260.00683620.006750.000983Toal0.056880.1534780.1156120.050716

4 结论

本文从太阳能电池单元的常用单/双二极管两种模型出发，通过ADE算法对模型参数辨识，根据太阳能电池单元模型拟合结果将单二极管模型作为光伏组件模型的基础，通过ADE算法辨识光伏组件模型参数。然后计算出功率进行拟合，由评价指标和拟合效果，可以看出，ADE算法能更精确地辨识太阳能组件模型参数，辨识后的模型能更好地拟合实测数据，并把辨识结果与其他辨识方法相比，均具有明显的优势，辨识结果更加准确。同时增加光伏组件其他两种工作情况进行辨识，辨识后的模型拟合效果也很好，验证了本文提出的算法对组件不同工作环境下都能准确有效地进行参数辨识。本文的研究方法对光发电系统仿真和实际光伏电厂最大功率点跟踪控制具有实际意义。但是实际光伏发电环境复杂多变(光照强度变化，温度变化，有遮挡)，课题组下一步准备通过硬件实现对光伏发电的实时测量，结合本文的方法对光伏发电最大功率点进行实时跟踪控制。

参考文献：

[1]张兴. 太阳能光伏并网发电及其逆变控制 [M]．北京：机械工业出版社，2011.

[2]简献忠, 魏凯, 郭强. 蜂群算法在光伏电池双二极管五参数模型中的应用[J]. 光子学报, 2015, 44(1): 1-5.

[3]YUAN X F, HE Y Q, LIU L J. Parameter extraction of solar cell models using chaotic asexual reproduction optimization[J]. Neural Comput & Applic, 2015, 26(5):1227-1239.

[4]ALRASHIDI M R, ALHAJRI M F, ELNAGAR K M, et al. A new estimation approach for determining the I-V characteristics of solar cells[J]. Solar Energy, 2011, 85(7):1543-1550.

[5]ABDELKADER A, RABIAA G,MOHAMED A D. An improved single-diode model parameters extraction at different operating conditions with a view to modeling a photovoltaic generator: a comparative study[J]. Solar Energy, 2017,155: 478-489.

[6]KASHIF I, ZAINAL S, SAAD M. Parameter extraction of solar photovoltaic modules using penalty-based differential evolution[J].Applied Energy,2012，99:297-308.

[7]SANTIAGO P, JAVIER C.Simple mathematical approach to solar cell/panel behavior based on datasheet information[J]. Renewable Energy，2017，103:729-738.

[8]SALEEM H, KARMALKAR S. An analytical methodto extract the physical parameters of a solar cell from four points on the illuminated J-V Curve[J]. IEEE Electron Device Letters ,2009,30 (4): 349-352.

[9]PENG L L, SUN Y Z, MENG Z. An improved model and parameters extraction for photovoltaic cells using only three state points at standard test condition[J].Journal of Power Sources, 2014,248:621-631.

[10]MENG J R， FENG J， SUN Q, et al. Degradation model of the orbiting current for GaInP/GaAs/Ge triple-junction solar cells used on satellite [J] . Solar Energy，2015, 122:464-471.

[11]EASWARAKHANTHAN T, BOTTIN J, BOUHOUCH I, et al. Nonlinear minimization algorithm for determining the solar cell parameters with microcomputers[J]. Sol Energy, 1986,4(1):1-12.

[12]JERVASE J A, BOURDOUCEN H, AL-LAWATI A. Solar cell parameter extraction using genetic algorithms[J]. Measurement Science and Technology, 2001,12 (11): 1922-1925.

[13]AIHAJRI M F，ELNAGGAR K M, ALRASHIDI M R，et al．Optimal extraction of solar cell parameters using paterm search [J]．Renewable Energy，2012，44(4)：238-245．

[14]SHONGWE S, HANIF M. Comparative analysis of different single-diode PV modeling methods[J]. IEEE Photovolt, 2015,5(3):938-946.

[15]ASKARZADEH A, REZAZADEH A. Artificial bee swarm optimization algorithm for parameters identification of solar cell models [J]. Applied Energy, 2013(102) :943-949.

[16]QIN H, KIMBALL W. Parameter determination of photovoltaic cells from field testing data using particle swam optimization[C]. Power and Energy Conference at Illinois(PECI), IEEE,2011:1-4．

[17]MARCANTONIO C,LORENZO C,MARIAN K, et al. Matlab PV solar concentrator performance prediction based on triple junction solar cell model[J]. Measurement,2016,88:310-317.

[18] ZHOU J L，WANG B，ZHANG Y M．Parameter identification and output power prediction of photovoltaic array based on the measured dataf[J]．Renewable Energy Resources，2012，30(7)：1-4．

[19] RATA Y，NORO S，AOKI T．Diagnosis photovoltaic failure by simple function method to acquire I-V curve of photovoltaic modules string[C]．Photovoltaic Specialists Conference (PVSC), 2012：1340-1343．

[20]郭鹏.差分进化算法的改进研究[D].天津；天津大学, 2011.

[21]BASTURK A，GUNAY E．Efficient edge detection in digital images using a cellular neural network optimized by differential evolution algorithm[J]. Expert Systems with Applications, 2009(36)：2645-2650.