横观各向同性黏弹性沥青路面的动力响应

鲁巍巍，郑健龙



横观各向同性黏弹性沥青路面的动力响应

鲁巍巍1, 2，郑健龙1

(1. 长沙理工大学 交通运输工程学院，湖南 长沙，410114； 2. 长沙理工大公路工程试验检测中心，湖南 长沙，410114)

为了更好地表征路面在荷载作用下的力学行为，研究考虑基层和土基材料的横观各向同性特性的黏弹性沥青路面在落锤式弯沉仪(fal1ing weight deflectometer，FWD)荷载作用下的动力响应。从各向同性黏弹性和横观各向同性弹性轴对称空间动力问题的基本控制方程出发，借助相应的积分变换，分别建立积分变换域内的各向同性黏弹性体的双节点层单元刚度矩阵和横观各向同性弹性体的双节点与单节点层单元刚度矩阵，进而得到考虑横观各向同性的黏弹性多层沥青路面结构的解析刚度矩阵解。通过求解横观各向同性问题退化的各向同性问题，并与已有解答进行对比，验证本文计算方法的准确性。然后，分析基层和土基的横观各向同性特性对路表弯沉的影响。研究结果表明：随着基层和土基模量比减小，路表弯沉增大，且基层模量比变化的影响更显著。

沥青路面；黏弹性；横观各向同性；动力响应；解析刚度矩阵法

横观各向同性体是物体内任意一点存在1个平面，在平行于该平面的所有各个方向都具有相同的弹性性质，且垂直于该平面的方向具有不同弹性的各向异性体。近年来，许多学者发现土体和粒料类基层材料具有明显的各向异性。路基土通常在天然沉积和压实填筑过程中或在复杂的应力状态下土颗粒的排列呈各向异性[1−2]。粒料类基层材料是由具有一定级配的不同形状集料组成，其内部结构通常呈明显的各向异性，这种各向异性特性主要是集料的分布、形状、方位和空隙结构及压实施工和交通荷载性质等因素造成 的[3]。GRAHAM等[4]的研究表明，对于黏性土，其水平方向与垂直方向的弹性模量比为0.9~4.0，而对于砂和碎石类粒料，其模量比降到0.2。LO等[5]通过碎石类材料试验发现随着主应力比增加，材料的各向异性特性更加明显。TUTUMLUER等[6]通过对不同类型粒料的研究分析，发现基层碎石类材料的水平向与竖直向的弹性模量比为3%~21%，其剪切模量与竖直向的弹性模量比为18%~35%。横观各向同性是一种特殊的各向异性表征，在分析路面结构的响应时，考虑路基和基层结构层材料的横观各向同性能获得更准确的路面力学响应[7−10]。另一方面，沥青混合料是一种典型的黏弹性材料，其材料性能与时间、温度和荷载作用频率等因素密切相关。基于弹性理论的沥青路面设计和分析会低估路面的响应，导致路面容易出现早期破损，而且弹性理论无法表征沥青混合料的永久变形及蠕变等重要特性而使路面容易出现车辙等病害，因此，考虑面层沥青混合料材料的黏弹性特性非常必要[11]。借助动力加载和现场测试获得沥青路面的真实力学响应，是正确评估路面性能特征并有效指导路面结构设计的重要途径[12]。随着科技的进步，有别于传统使用的贝克曼梁，落锤式弯沉仪(fal1ing weight deflectometer，FWD)近些年来在道路工程检测领域被广泛应用，它能较好地模拟实地行车荷载对路面的动力作用，快速、准确地检测和评价路面各结构层或路基的强度。尽管近年来关于沥青路面结构动力分析的研究成果较多[11−13]，但大多是基于各向同性层状弹性或黏弹性体系的路面结构。为此，本文作者将沥青面层视为黏弹性，并考虑基层和土基材料的横观各向同性特性，结合刚度矩阵法计算精度高而且稳定性强等特点，采用解析法求解沥青路面在FWD动荷载下的力学响应方程，并分析基层和土基材料各向异性特性对动力响应的影响[14−15]。

1 层单元刚度矩阵推导

1.1 各向同性黏弹性轴对称动力问题层单元刚度 矩阵

在柱面坐标系中，用位移表示的黏弹性轴对称空间动力问题的控制方程为[16]

首先应用Stieltjes卷积的Laplace变换式对式(2)进行关于时间的Laplace变换。然后，对式(1)中两式分别进行关于径向坐标的一阶和零阶Hankel变换，得到[17]：

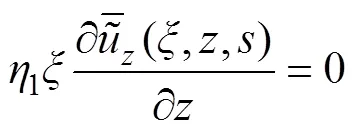
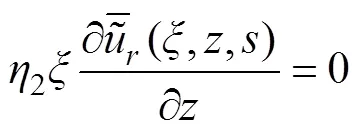
采用如下假设：

即在初始时刻物体的位移、速度和加速度均等于0。通过Laplace变换消去控制方程中关于时间的偏导数。

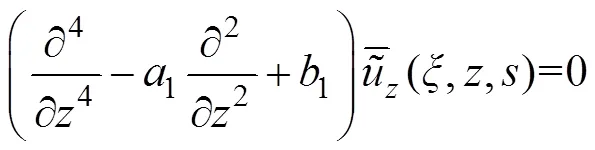
其中：

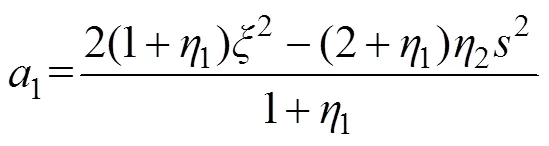
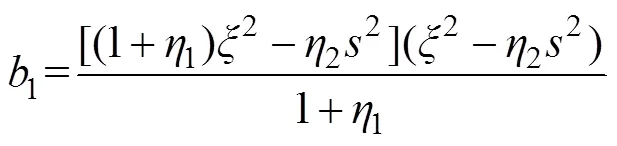
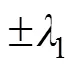
黏弹性轴对称空间问题的物理方程为[17]

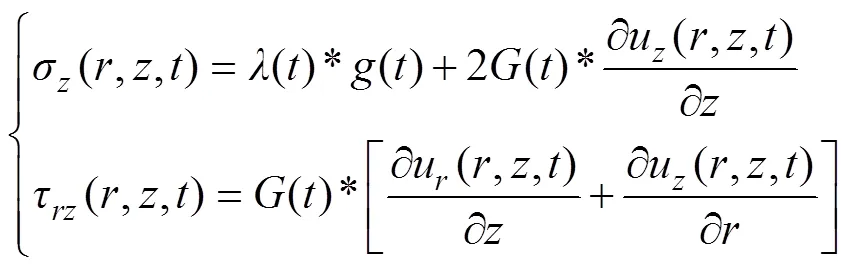
式中：为正向应力；为剪应力。

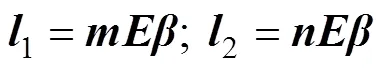
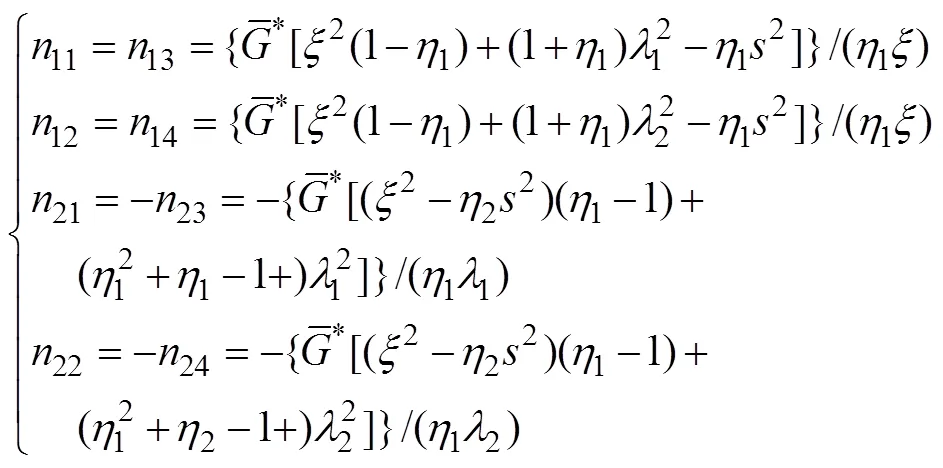
将每个结构层视为1个层单元，作为研究对象。在轴对称问题中，双节点层单元示意图如图1所示，其中，上标1和2分别表示单元上、下表面边界。

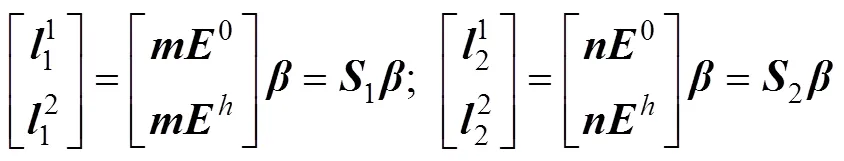
根据Cauchy应力原理，节点外力向量可以通过节点应力张量点乘单位面外法线矢量得到。结合有限元分析(FEM)中刚度矩阵的概念即刚度矩阵建立单元节点外力和节点位移的关系，可得

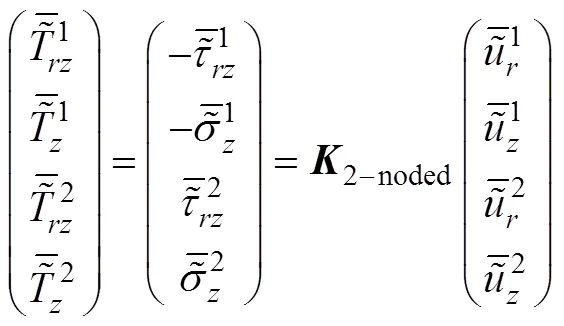
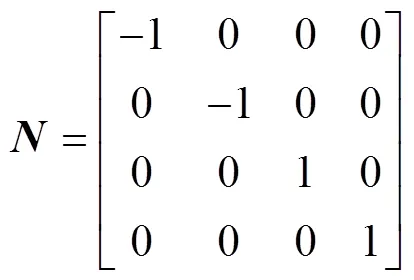
1.2 横观各向同性弹性体轴对称动力问题层单元刚度矩阵

弹性空间轴对称动力问题运动平衡微分方程为

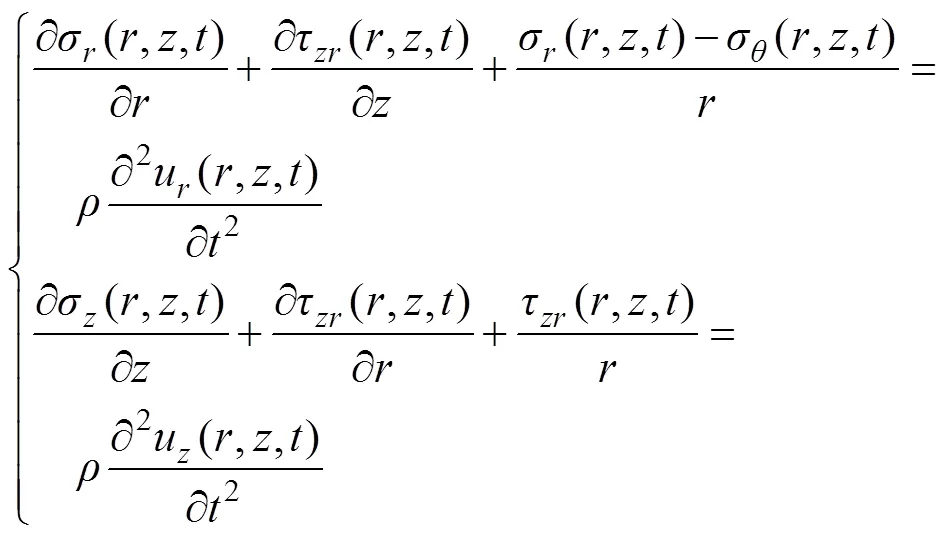
几何方程为

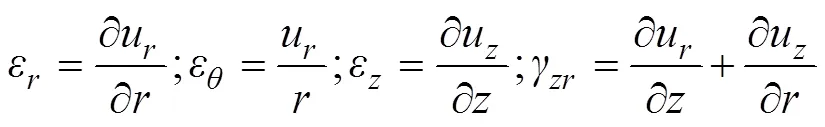
横观各向同性弹性体的应力与应变关系可以用如下形式来表示：

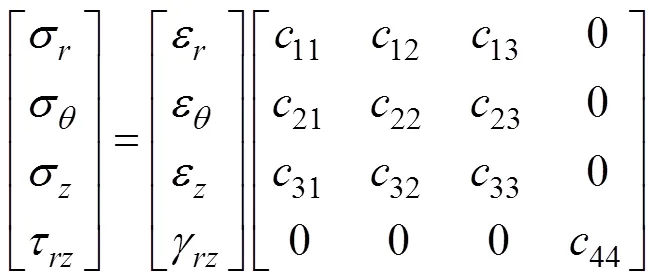
联立式(13)，(14)和(15)可以得到位移表示的横观各向同性弹性空间轴对称动力问题的控制方程：

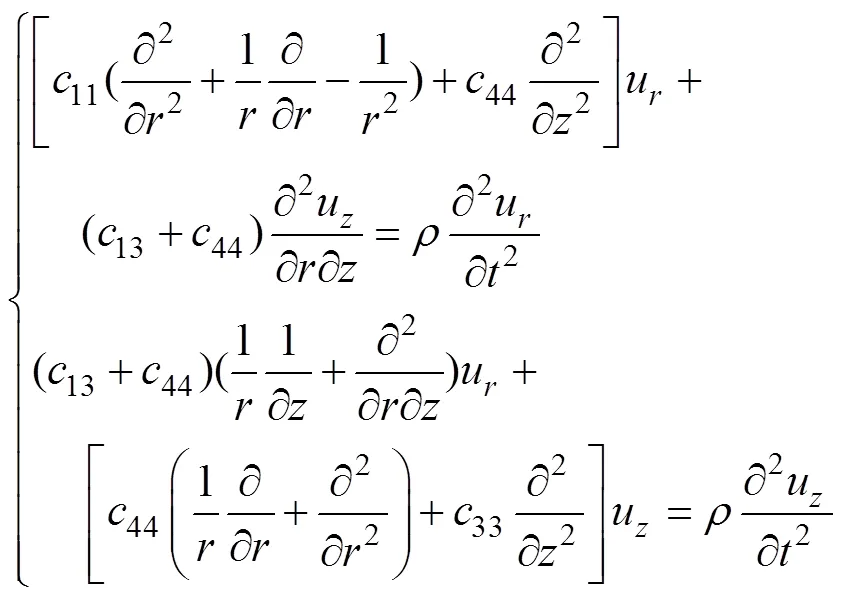
对式(16)先进行关于时间的Laplace变换，然后，对其中两式分别进行关于径向坐标的一阶和零阶Hankel变换，可得

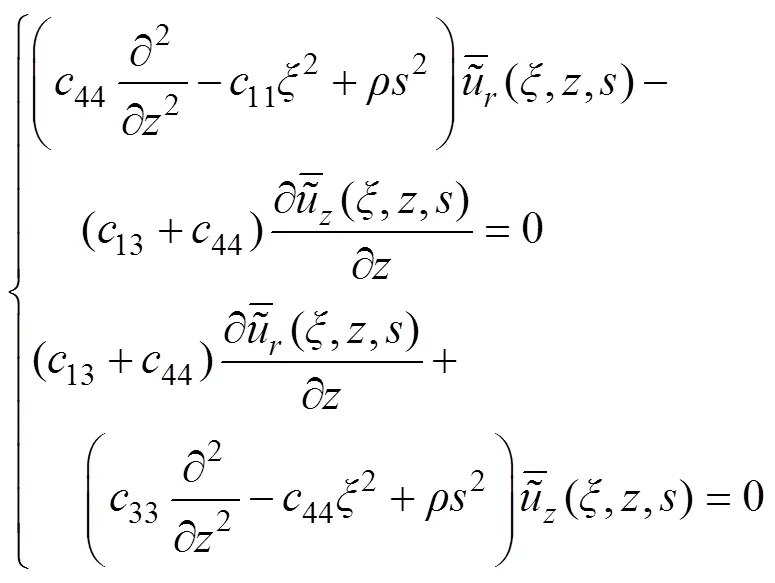
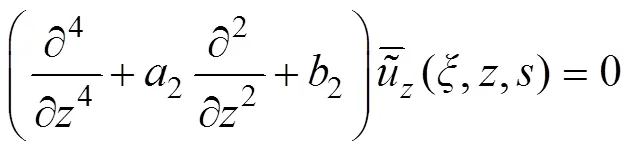
其中：

可以得到其通解为

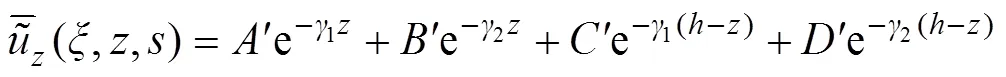
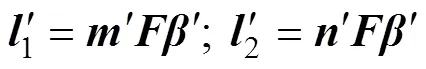
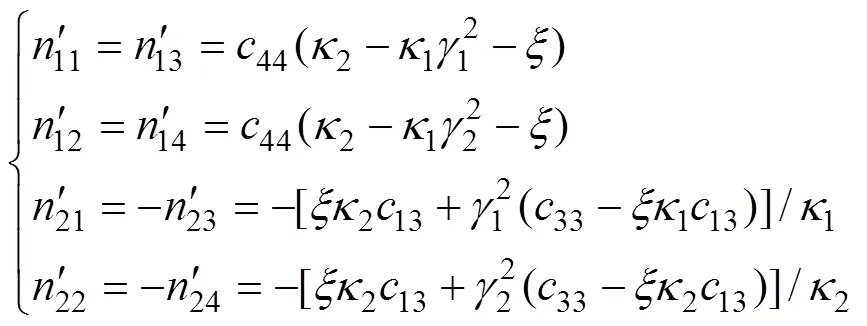
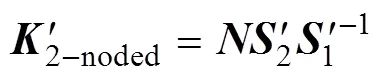
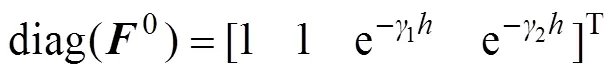
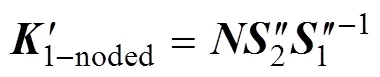
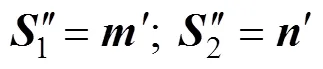
2 考虑横观各向同性的黏弹性沥青的多层路面结构求解

FWD荷载为冲击荷载，荷载作用时间一般只有0.03~0.04 s。FWD荷载对路面的冲击作用可以用如下半正弦函数来描述：

式中：为荷载圆半径(m)；0为荷载峰值(MPa)；为加载总时间(ms)。

假设路表受FWD冲击荷载，则其上表面的边界条件为

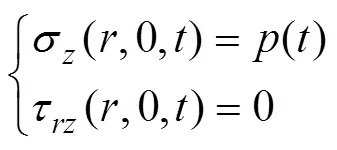
将轴对称各向同性黏弹性空间静力问题(表示沥青面层)的双节点层单元刚度矩阵、横观各向同性弹性空间静力问题的有限层(表示基层)和半无限体(表示土基)的单层刚度矩阵用于各计算层，并假定路面各结构层间完全连续，按照FEM中的对号入座原则集成整个多层路面体系的总体刚度矩阵为

式中：(i)为第层刚度矩阵。

建立了总体刚度矩阵后，可以通过以下关系式求解总体节点位移：

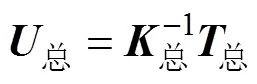
当路面表面仅受竖直向下的荷载时，根据边界条件可知：

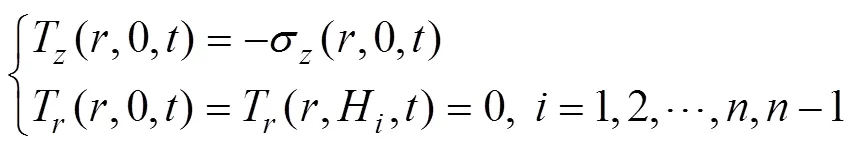
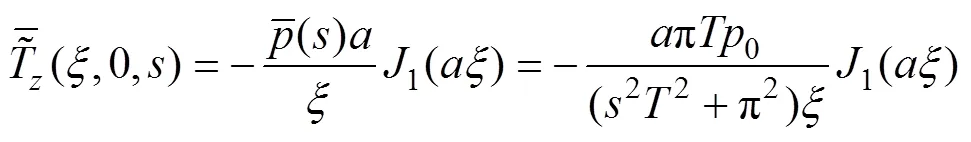
最后借助相应的积分逆变换就可以得到物理域内的解。

3 验证与计算分析

3.1 验证

为了验证本文解析刚度矩阵解的准确性，将横观各向同性问题退化为各向同性问题。将退化各向同性问题的解与任瑞波等[12]的传递矩阵解的计算结果进行对比。

计算结构为3层沥青路面结构。沥青面层材料黏弹性性质采用Burgers模型来描述，其本构方程为

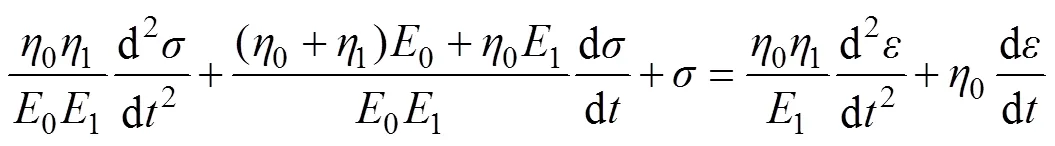
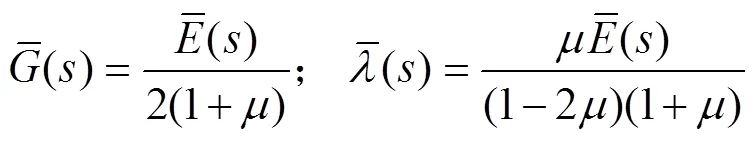
沥青面层的厚度为18 cm，其黏弹性材料力学参数弹性模量0=1=2 300 MPa，黏度1=2=2.06×105Pa∙s，密度1=2.1 t/m3，泊松比1=0.25。基层与土基均为各向同性弹性体，基层厚度为35 cm，弹性模量2=910 MPa，泊松比2=0.25，密度2=2.0 t/m3。土基弹性模量3=100 MPa，泊松比3=0.25，密度3=1.9 t/m3。FWD荷载参数为：荷载圆半径=0.15 cm，荷载峰值0=0.721 MPa，加载总时间=32 ms。这里的路面结构和材料参数与文献[11]中的一致。

本文采用与文献[12]中相同的Hankel积分和Laplace积分数值反演的方法。采用本文退化的解析刚度矩阵解与文献[11]中传递矩阵解计算的FWD荷载作用下落锤中心处(=0)弯沉时程见图3。由图3可知：本文计算路表弯沉与文献[11]中的结果很吻合。

1—本文结果；2—文献[11]中结果。

3.2 计算分析

文献[11]分析了FWD动荷载作用下沥青路面层状体黏弹解与弹性解的差异，本文着重分析材料横观各向同性特性的影响。横观各向同性材料主要参数包括竖向弹性模量v､水平向弹性模量h､竖直向应力引起的水平向应变的泊松比vh､水平向应力引起的正交水平向应变的泊松比h､竖直面上的剪切模量v(通常假定竖向和水平向剪切模量相等[14])。在路面力学分析计算中，通常假定vh=h，v=v/[2(1+vh)][14]，并引入参数模量比(=hv)来表征材料的横观各向同性特性。本文主要探讨基层和土基的横观各向同性特性对黏弹性沥青路面的动力弯沉的影响。路面结构和材料参数与验证部分的参数相同，但考虑基层和土基应为横观各向同性，它们的竖向模量分别与验证部分的各自弹性模量取相同值，并依据文献[2]，基层模量比2取为0.25，0.50，0.75和1.00，土基模量比3取为0.50，1.00，2.00和4.00。

当基层和土基模量比不同时，在FWD荷载作用下，落锤中心处(=0)的路表弯沉时程曲线分别见图4和图5。从图4和图5可见：随着基层和土基的模量比减小即水平向模量减小，路表弯沉变大，且基层模量比的变化影响非常显著。忽略路基路面材料的横观各向同性特性会使路表弯沉计算会产生偏差，从而基于路表弯沉的路面材料模量反算也会产生一定的误差。

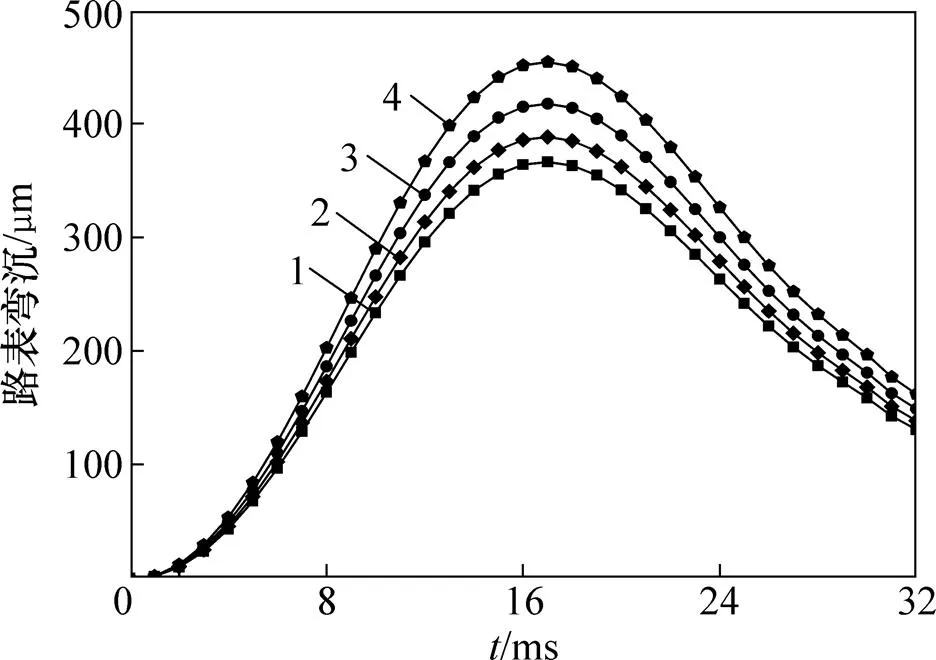
n2：1—1.00；2—0.75；3—0.50；4—0.25。

n3：1—0.50；2—1.00；3—2.00；4—4.00。

4 结论

1) 从各向同性黏弹性和横观各向同性弹性轴对称空间动力问题的基本控制方程入手，分别建立了积分变换域内的各向同性黏弹性体的双节点层单元刚度矩阵和横观各向同性弹性体的双节点与单节点层单元刚度矩阵，进而得到考虑考虑横观各向同性的黏弹性多层沥青路面结构动力问题在积分变换域内的解析刚度矩阵解，最后应用相应的积分变换数值反演方法，得到物理域内的解。

2) 为了验证本文动力解析解的准确性，将考虑横观各向同性的沥青路面黏弹性静力问题解析解退化到各向同性问题的解，并与已有的解析解进行计算对比，结果显示解析解具有很高的准确性。

3) 随着基层和土基的模量比减小即水平向模量减小，路表弯沉变大，且基层模量比变化的影响更 显著。

[1] WANG L, HOYOS L R, WANG J, et al. Anisotropic properties of asphalt concrete: characterization and implications for pavement design and analysis[J]. Journal of Materials in Civil Engineering, 2015, 17(5): 535−543.

[2] YOU L, YAN K, HU Y, et al. Spectral element solution for transversely isotropic elastic multi-layered structures subjected to axisymmetric loading[J]. Computers & Geotechnics, 2016, 72: 67−73.

[3] WANG H, AL-QADI I L. Importance of nonlinear anisotropic modeling of granular base for predicting maximum viscoelastic pavement responses under moving vehicular loading[J]. Journal of Engineering Mechanics, 2013, 139(1): 29−38.

[4] GRAHAM J, HOULSBY G T. Anisotropic elasticity of a natural clay[J]. Geotechnique, 1983, 33(2): 165−180.

[5] LO S C R, LEE I K. Response of granular soil along constant stress increment ratio path.[J]. Journal of Geotechnical Engineering, 1990, 116(3): 355−376.

[6] TUTUMLUER E. Anisotropic behavior of unbound aggregate bases-state of the art summary[C]//Proceedings of the 6th Annual Symposium of the International Center for Aggregate Research ICAR. St. Louis, Missouri, 1998.

[7] OH J H, LYTTON R L, KIM N S. Modeling of pavement response using nonlinear cross-anisotropic approach[J]. KSCE Journal of Civil Engineering, 2005, 9(4): 329−332.

[8] MASAD S, LITTLE D, MASAD E. Analysis of flexible pavement response and performance using isotropic and anisotropic material properties[J]. Journal of Transportation Engineering, 2006, 132(4): 342−349.

[9] YOU L, YAN K, HU Y, et al. Spectral element method for dynamic response of transversely isotropic asphalt pavement under impact load[J]. Road Materials & Pavement Design, 2018, 19(1): 223−238.

[10] YAN K, XU H, YOU L. Analytical layer-element approach for wave propagation of transversely isotropic pavement[J]. International Journal of Pavement Engineering, 2016, 17(3): 275−282.

[11] 吕彭民, 董忠红. 车辆−沥青路面系统力学分析[M]. 北京: 人民交通出版社, 2010: 85−93. LÜ Pengmin, DONG Zhonghong. Mechanical analysis of vehicle-asphalt pavement system[M]. Beijing: China Communications Press, 2010: 85−93.

[12] 任瑞波, 谭忆秋, 张肖宁. FWD动荷载作用下沥青路面层状粘弹体路表弯沉的求解[J]. 中国公路学报, 2001, 14(2): 9−12. REN Ruibo, TAN Yiqiu, ZHANG Xiaoning. Solution for solving asphalt pavement multilayered viscoelastic body surface deflection in the FWD dynamic case[J]. China Journal of Highway and Transport, 2001, 14(2): 9−12.

[13] LEE H S. Viscowave: a new solution for viscoelastic wave propagation of layered structures subjected to an impact load[J]. International Journal of Pavement Engineering, 2014, 15(6): 542−557.

[14] LIU N, YAN K, SHI C, et al. Influence of interface conditions on the response of transversely isotropic multi-layered medium by impact load.[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2018, 77: 485−493.

[15] 郭大智, 任瑞波．层状黏弹性体系力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2001: 31−38. GUO Dazhi, REN Ruibo. Layered viscoelasticity system mechanics[M]. Harbin: Harbin Institute of Technology Press, 2001: 31−38.

[16] ZHANG X, LIU L, WIWATANAPATAPHEE B, et al. The eigenvalue for a class of singular p-Laplacian fractional differential equations involving the riemann–stieltjes integral boundary condition[J]. Applied Mathematics and Computation, 2014, 235(4): 412−422.

[17] GUPTASARMA D, SINGH B. New digital linear filters for Hankel J0 and J1 transforms[J]. Geophysical Prospecting, 1997, 45(5): 745−762.

(编辑 陈灿华)

Dynamic response of cross-anisotropic viscoelastic asphalt pavement

LU Weiwei1, 2, ZHENG Jianlong1

(1. School of Traffic and Transportation Engineering, Changsha University of Science & Technology, Changsha 410114, China; 2. Test Centre for Highway Engineering, Changsha University of Science & Technology,Changsha 410114, China)

In order to better characterize the mechanical behavior of the pavement under fal1ing weight deflectometer (FWD for short) load, the dynamic responses of viscoelastic asphalt pavement were analyzed considering the cross-anisotropy of unbound aggregates bases (UAB for short) and subgrades. Based on the governing equations for isotropic viscoelastic and cross-anisotropic elastic axisymmetric spatial dynamic problems, the stiffness matrixesin the integral transform domain of 2-nodedlayer elementfor the isotropic viscoelastic body and 2-noded and 1-noded layer elements for the cross-anisotropic elastic body were developed respectively, and then the analytical stiffness matrix solution of viscoelastic multi-layered asphalt pavement structure considering cross-anisotropy was proposed. The validity of the developed method was verified by comparing the results of cross-anisotropic problem reducing to isotropic problem with the existing solutions. Subsequently, the influences of cross-anisotropy of UAB and subgrade on the surface defections were investigated. The results show that surface defections increase with the decrease of modulus ratios of UAB and subgrades, and the ratios of modulus of UAB have more significant impacts.

asphalt pavement; viscoelasticity; cross-anisotropic; dynamic response; analytical stiffness matrix solution

U416.217

A

1672−7207(2018)04−0964−07

10.11817/j.issn.1672−7207.2018.04.026

2017−07−10；

2017−09−12

交通运输部建设科技项目(2015318825120)(Project (2015318825120) Supported by the Ministry of Transport Construction Projects of Science and Technology)

鲁巍巍，高级工程师，从事道路工程路基路面工程研究；E-mail：13619845@qq.com