提高“天绘一号”卫星条带影像拼接精度的技术探讨

程家胜 穆春迪 李扬 姜艳媛



提高“天绘一号”卫星条带影像拼接精度的技术探讨

程家胜 穆春迪 李扬 姜艳媛

（中国天绘卫星中心，北京 102102）

“天绘一号”卫星2m全色相机焦平面共8片TDI-CCD器件，分上下两行品字形交错排列组成。目前地面处理系统采用基于SIFT特征点匹配的分段线性拼接算法，将8片条带影像进行拼接。然而受地形起伏、云层移动、影像对比度等多种因素影响，易出现局部拼接错位现象，条带拼接精度不高，降低了卫星的使用性能。为解决上述问题，文章重点分析了影响拼接精度的因素，并提出了基于分段线性拼接和拼接区域逻辑自适应影像增强技术的影像拼接方法。经过大量试验验证，该方法有效地解决了长条带影像拼接参数不一致、拼接区域影像对比度不高等问题，提高了器件片间拼接精度，在“天绘一号”卫星条带影像的拼接中取得了良好的应用效果。

尺度不变的特征转换算法 分段线性拼接 影像增强 “天绘一号”卫星 空间遥感应用

0 引言

时间延迟积分电荷藕合器件图像传感器（Time Delay Integration Charge Coupled Device，TDI-CCD）是一种面阵结构、线阵输出的新型CCD，由于单片TDI-CCD像素个数有限，在相机设计时，为解决空间分辨率和成像幅宽的矛盾，需将多片TDI-CCD连接排列。“天绘一号”卫星2m全色相机焦面共8片TDI-CCD，采用视场中心线两侧分上下两行交错排列，相邻TDI-CCD器件的视场拼接方式分两排安装。星下采用基于尺度不变特征转换（Scale-Invariant Feature Transform，SIFT）算法在相邻TDI-CCD影像上提取匹配点，统计得到片间水平偏移量和垂直偏移量，然后依次对相邻两片影像进行拼接处理，以形成覆盖整个相机有效视场的连续无缝的扫描景[1-3]。但在实际应用中发现，受地形起伏、云层移动、影像对比度等因素影响，拼接精度不高，降低了卫星的使用效能。文献[4-6]提出基于SIFT的图像匹配算法，但算法针对全部图像采用同一拼接参数，不适用于长条带影像；文献[7]提出了一种基于RANSAC （Random Sample Consensus）特征点提纯技术的SIFT匹配算法，虽然算法匹配精确度较好，但复杂度较高，不适用于长条带遥感影像处理；文献[8-10]提出了一种简化SIFT算法，但算法对低对比度影像处理效果有限。

因此，本文重点分析了影响拼接精度的因素，并提出通过引入分段线性拼接、拼接区域逻辑自适应影像增强技术提高拼接精度。经验证，该方法有效提高了产品的拼接精度，并在“天绘一号”卫星条带影像的拼接中取得了良好的应用效果。

1 SIFT算法简介

由于SIFT算法在相关文献上有详细介绍，本文只结合其在“天绘一号”卫星条带拼接中的具体应用进行简单介绍。

SIFT特征匹配方法，是由Lowe在总结现有的基于变量技术的特征提取方法基础上，提出的一种基于尺度空间局部特征的描述算子[11]，该算子对于匹配图像间的旋转、平移、拉伸等仿射变换具有良好的鲁棒性。“天绘一号”卫星基于SIFT算法的条带拼接流程主要环节如图1所示，图中虚线框内的主要步骤是经典的SIFT算法[12]，由于“天绘一号”卫星相机结构的特殊性，在SIFT算法需找到匹配点后，分段对影像进行拼接，并对拼接接缝处进行了灰度平滑处理。

图1 SIFT算法主要环节

（1）尺度空间极值检测

尺度空间（scale space）是一个抽象的框架，从算法的观点看是滤波器的迭代，尺度空间理论的目的是模拟影像数据的多尺度特征。高斯卷积核是实现尺度变换的唯一线性核，二维影像的尺度空间函数(,,)定义为：

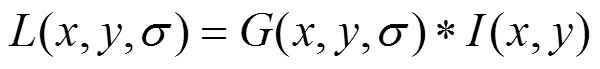
式中(,)代表影像；(,,)是尺度可变高斯函数，其表达式如下：

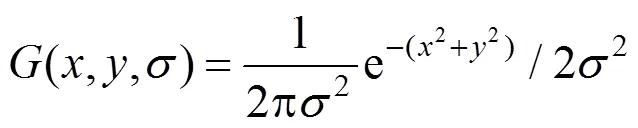
式中 (,)是像素点的空间坐标；是尺度坐标。

（2）尺度空间关键点提取

由于关键点的提取是在尺度空间中进行的，相比较传统特征点的检测方法，SIFT特征点不仅包含了点影像坐标，还包含了尺度。为了进一步增强匹配稳定性、提高抗噪声能力，SIFT算法采用了多种处理方法实现特征点的亚像素精度定位，同时去除了容易受噪声影响的低对比度的关键点和不稳定的边缘响应点[15-18]。

（3）关键点方向分配

利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数，使算子具备旋转不变性。

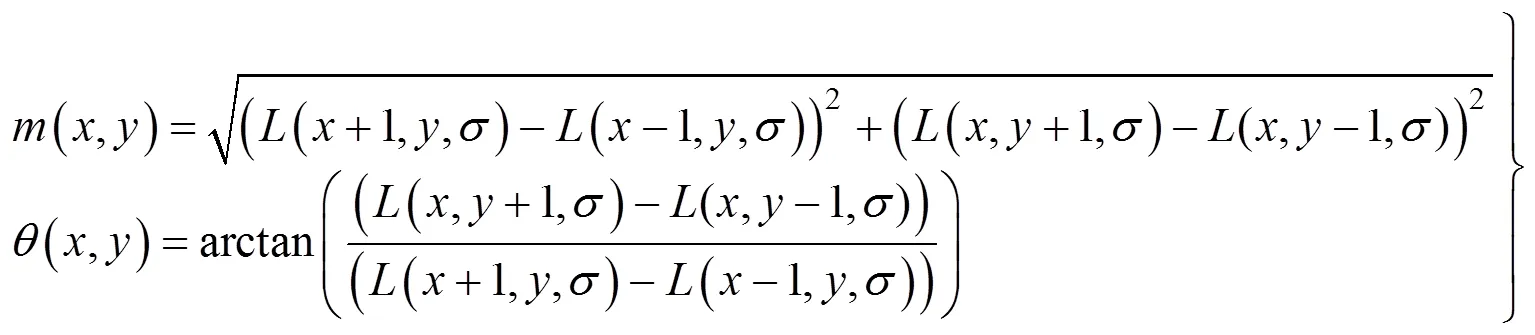
式中(,)为(,)处梯度的模值；(,)为(,)处方向公式。其中函数所用的尺度为每个关键点各自所在的尺度。

（4）特征点匹配

当生成了两幅影像的SIFT特征向量，利用关键点特征向量的欧氏距离作为相似性度量。取影像1中的某个关键点，并找出其与影像2中欧氏距离最近的两个关键点。在这两个关键点中，若最近距离与次近距离比值小于设定的阈值，则认为它们是一对匹配点。降低这个比例阈值，SIFT匹配点数目会减少，但更加稳定。

（5）剔除误匹配点

由于影像中的噪声等因素干扰，通过SIFT所提取的特征点对并不都正确。对于错误的特征点在求解几何变换参数时影响很大，所以需要采取一定的措施剔除无效的干扰点对（干扰点对：指算法判定当前点为匹配点，但实质上是错误匹配的点），即所谓的外点。“天绘一号”卫星采用RANSAC算法剔除误匹配点，RANSAC算法是根据一组包含异常数据的样本数据集，计算出数据的数学模型参数，得到有效样本数据的算法。RANSAC是一种具有鲁棒性的参数估计方法，可以处理外点比例大于50%的数据集。

2 影响拼接精度原因分析

由于影响“天绘一号”卫星条带拼接精度的因素与相机的安装结构有很强的相关性，所以在分析影响拼接精度原因之前，先介绍“天绘一号”卫星2m分辨率全色相机的TDI-CCD器件物理安装结构。

“天绘一号”卫星2m分辨率全色相机焦面共有8片TDI-CCD器件，采用视场中心线两侧分上下两行交错排列，相邻两TDI-CCD器件搭接96个像素，两行CCD器件中轴线间距为2 114个像素。其几何关系如图2所示。

图2 TDI-CCD器件安装示意

卫星摄影期间需进行偏流角控制，保证相邻两片TDI-CCD器件间的搭接像素数量，便于影像拼接处理。

（1）地形起伏对拼接精度的影响

在卫星推扫成像过程中，由于地形起伏，导致传感器空间成像的几何关系产生改变，所拍摄的影像也产生了相应的形变，这种形变是引起拼接误差的主要因素之一，称之为像点位移。针对“天绘一号”卫星，经推算，地形起伏每增加233m，线阵之间就会错位1个像素。

（2）云层移动对拼接精度的影响

云的移动速度一般为10m/s~30m/s左右，最大云速可以达到49m/s。通过计算得到，对于一般的云速，同一块云所成像的位置差异达到3.23~9.68个像素点，当云速最大时，最大位置差异可达16个像素点。可见，假设在相邻两片CCD进行拼接时，在重叠区域中有云层存在，并且在云上或云的周围找到特征点时，那么通过这些特征点得到的拼接参数会对拼接精度产生较大影响。

如果公益性的劳务派遣制度能够切实执行上述功能，那么其最显著的效果将是保护农民免受损失，使其不至于返贫，从长远看，也有利于移民的非农就业正常化。

（3）对比度对拼接精度的影响

对于两片CCD器件之间的重叠区域地物变换不明显，或者由于大气干扰、探元响应度较低等因素造成影像质量下降，此时通过SIFT算法提取的特征点数较少，甚至部分重叠区无法找到有效的匹配点对。另外，“天绘一号”卫星获取的部分高纬度地区影像，由于太阳高度角低，影像整体较暗，条带拼接精度也较差。通过对拼接过程数据的分析，结合SIFT算法原理发现，SIFT算法寻找特征点的核心主要是依据灰度梯度的变化。对于整体灰度值偏暗、对比度低的影像，重叠区域内找到的特征点较少，经过粗差剔除后剩下的较少匹配点方差较大，导致最终计算出的片间拼接参数不准确，影响了图像的拼接精度。

3 提高拼接精度的主要技术途径

影响“天绘一号”卫星2m分辨率全色相机影像条带间拼接精度的因素是多方面的，本节主要针对地形起伏、对比度低的问题，提出了分段线性拼接、拼接区域逻辑自适应增强技术，并进行试验验证。

（1）分段线性拼接技术

由于“天绘一号”卫星2m分辨率全色相机的单景影像行数较大，加之受卫星平台稳定性、偏流角控制精度、地形起伏等因素的影响，往往导致每景影像用一个统一的拼接参数无法达到较好的拼接效果，即出现局部拼接错位的现象，如图3所示。

图3 整景采用统一参数拼接效果

因此，在“天绘一号”卫星2m分辨率全色相机影像条带拼接时，采用了分段拟合的方法来解决拼接参数不一致的问题。影像拼接方法详见图4。

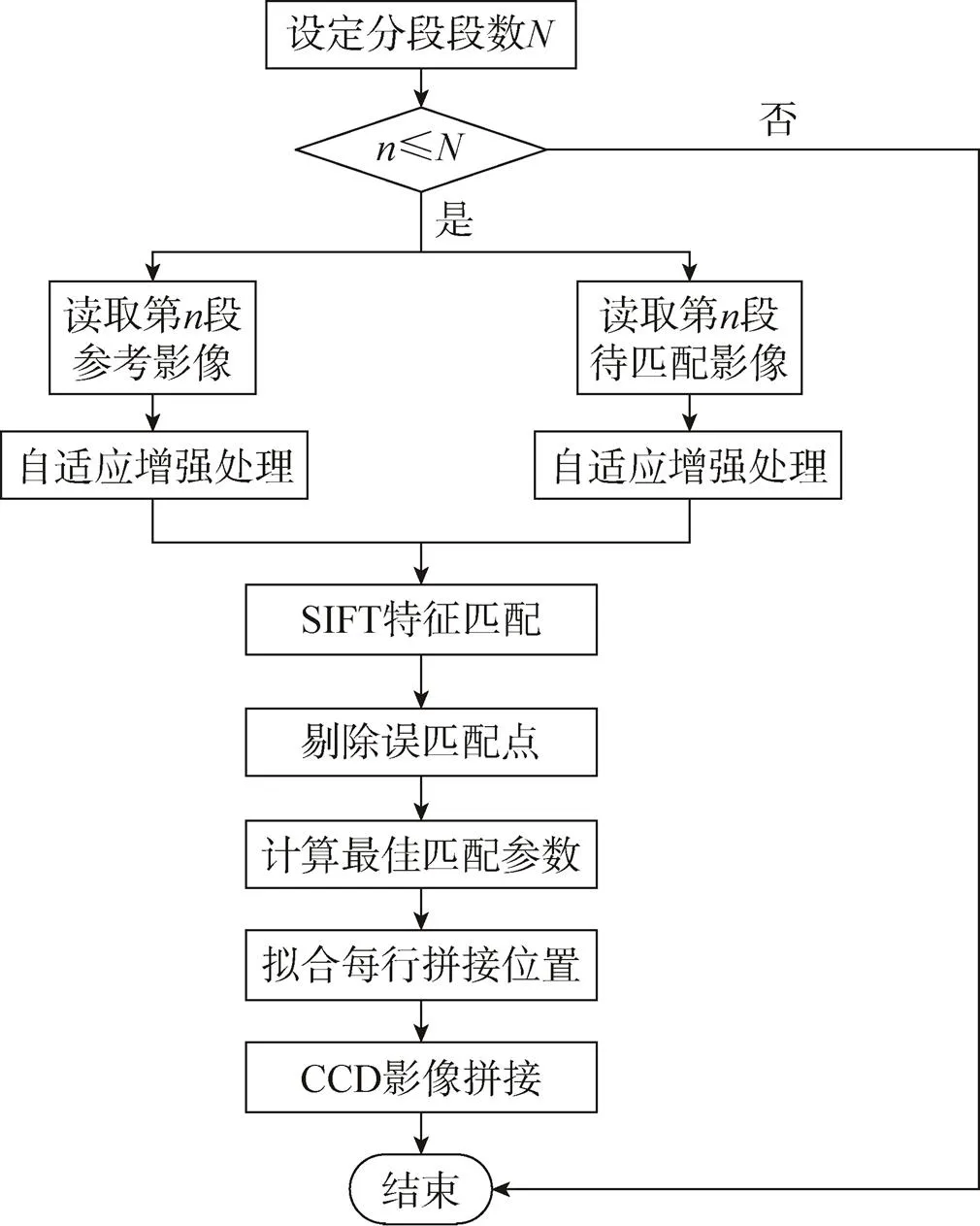
图4 基于SIFT算法的影像拼接流程

采用分段线性拼接技术后，作者选取了部分拼接精度达到指标要求的影像，并计算出每段的拼接参数。结果发现，每段的拼接参数有一定的波动，总体呈现缓慢变化的趋势，所以进一步得出“天绘一号”卫星必须采用分段线性拼接的方式，整景采用统一的参数必然导致局部拼接精度不高的结论。

3.2 拼接区域逻辑自适应增强技术

SIFT算法的核心是根据影像灰度的变化寻找特征点，提高影像的对比度，有利于特征点的寻找，进而可提高拼接精度。基于这一思想，在“天绘一号”卫星条带拼接处理之前，先对待拼接区域影像进行自适应逻辑影像增强，提高影像的对比度。

本文先建立直角坐标系，设定CCD相机安装面为轴、卫星飞行方向为轴（此处轴、轴的定义主要是依据相机的物理结构和卫星的飞行方向定义）。预处理系统接收到条带影像后，首先根据相机的物理结构读取相邻两条带的重叠区，“天绘一号”卫星相邻两条带轴方向重叠96个像素，故系统相邻两条带各读取110个像素。然后依次计算每段影像的灰度值范围，根据灰度值区间范围自动进行灰度值拉伸；之后基于SIFT算法寻找匹配点，经过粗差剔除后计算拼接参数。拼接区域逻辑自适应增强技术流程如图6所示。

图5 分段拼接效果

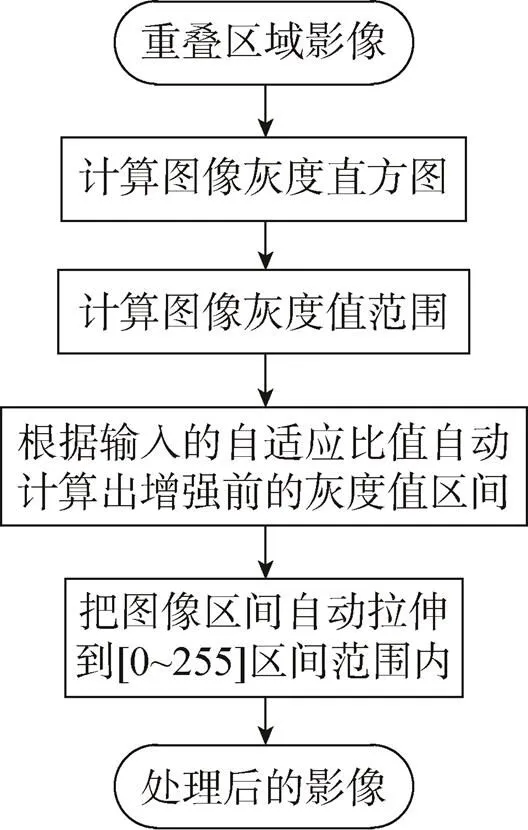
图6 影像自适应增强流程

Fig.6 Adaptive enhancement process of image

图7为拼接区域逻辑自适应增强前、后SIFT算法找到的匹配点。左图为未经过自适应逻辑增强找到的匹配点，右图为经过自适应逻辑增强后找到的匹配点。从图7可以看出，经过拼接区域逻辑自适应增强处理后，拼接区域的匹配点明显增多，理论上匹配点越多，根据匹配点计算出的拼接参数越准确，拼接精度将越高。

图7 自适应增强前后匹配点对

为验证上述结论的正确性，本文随机选取了“天绘一号”02星2017年6月18日拍摄的法国西部地区影像进行试验验证。图8为拼接区域逻辑自适应增强前后的拼接参数（为便于显示，只截取了前64段拼接区拼接参数），横轴为分段序号，纵轴为对应的拼接参数值（单位：像素）。

卫星平台在正常情况下是比较稳定的，拼接参数的变化应该是缓慢的，波动较大的参数属于异常值。从图8的拼接参数输出结果看，自适应增强处理前拼接参数波动较大；拼接区域逻辑自适应增强后，拼接参数波动明显变小。波动较大的拼接参数属于异常值，如果用异常拼接参数直接进行拼接，势必导致拼接精度下降。为验证此观点，本文对图8中自适应增强处理前、后的拼接情况进行了拼接精度对比检查。结果发现，拼接区域逻辑自适应增强后，拼接精度明显提高，如图9所示。

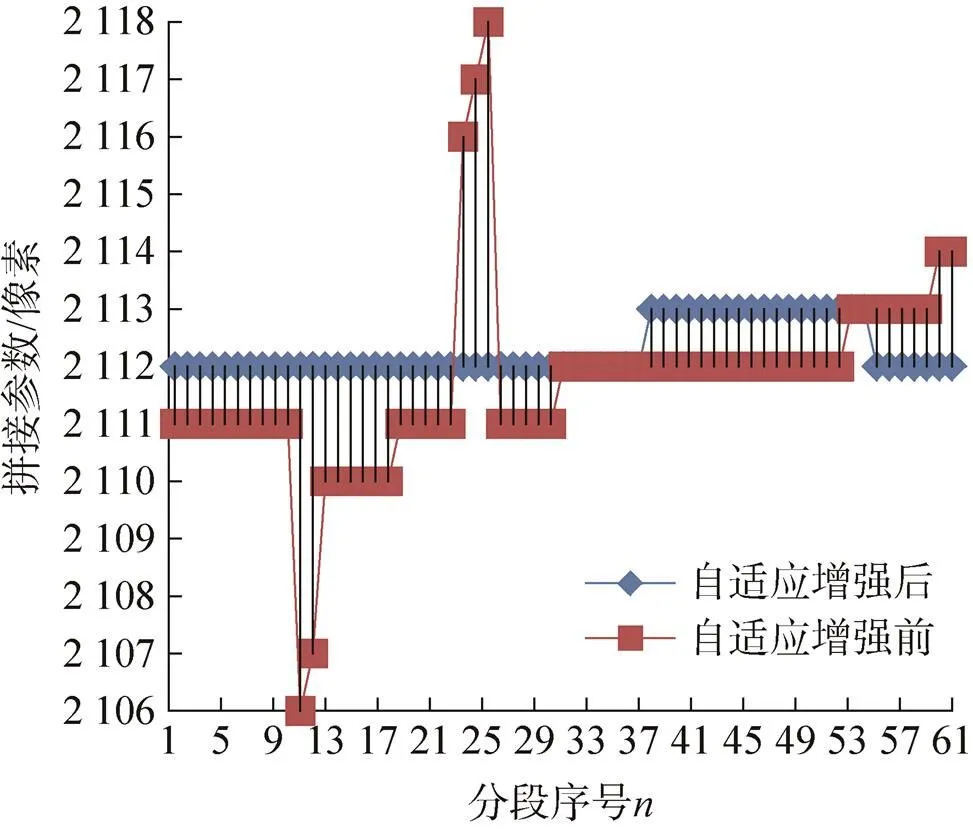
图8 自适应增强处理前后拼接参数对比

图9 自适应增强处理前后局部拼接效果

拼接区域逻辑自适应增强技术已经在“天绘一号”卫星数据预处理系统中得到工程化应用。经统计，该技术的成功应用有效提高了“天绘一号”卫星2m分辨率全色相机的影像条带间拼接精度。

在此需说明，拼接区域影像自适应增强的目的是用于计算拼接参数，最终的拼接区影像是通过对增强处理前的影像采样获取，所以称为拼接区域逻辑自适应增强。

3.3 测试结果

为验证分段线性拼接技术和拼接区域逻辑自适应增强技术对“天绘一号”卫星2m分辨率全色相机的影像条带间拼接效果，本文针对“天绘一号”卫星01、02星2017年10月、11月摄影的云量小于20%的有效数据进行了对比测试。

为便于描述，文中未采用分段线性拼接技术和拼接区域逻辑自适应增强技术的算法称为旧算法；采用分段线性拼接技术和拼接区域逻辑自适应增强技术的算法称为新算法。测试过程中，对于同一景数据，分别采用新、旧算法进行拼接，后采用相同的检测手段进行拼接精度检查。本文中，对拼接精度大于1个像素的数据视为不合格产品，称为错位数据。测试结果如表1和图10所示。表1中单月错位率为单月错位景数占单月总检测景数的百分比；合计错位率为两月错位景数之和占两月总检测景数的百分比。

表1 新、旧算法拼接错位率测试结果

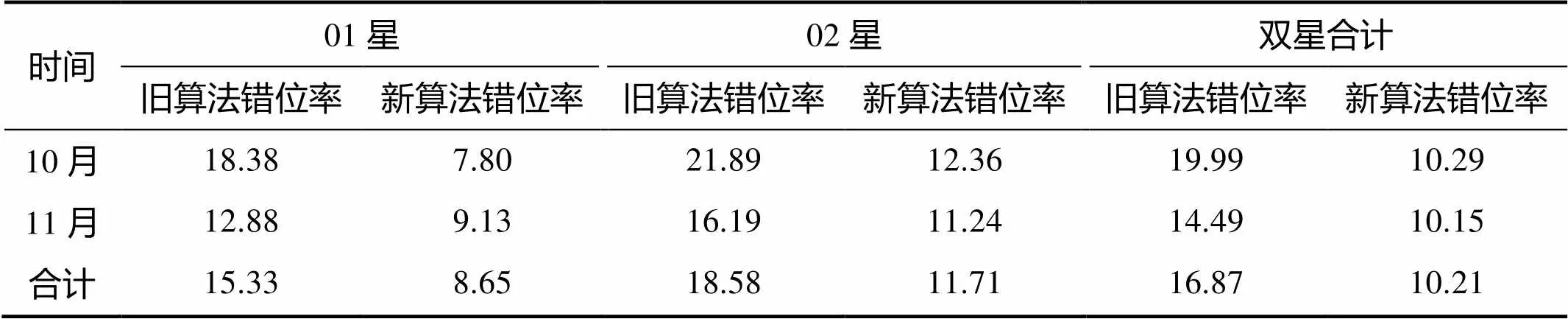
Tab.1 Test results of stitching misplacement rate of new and old algorithms %

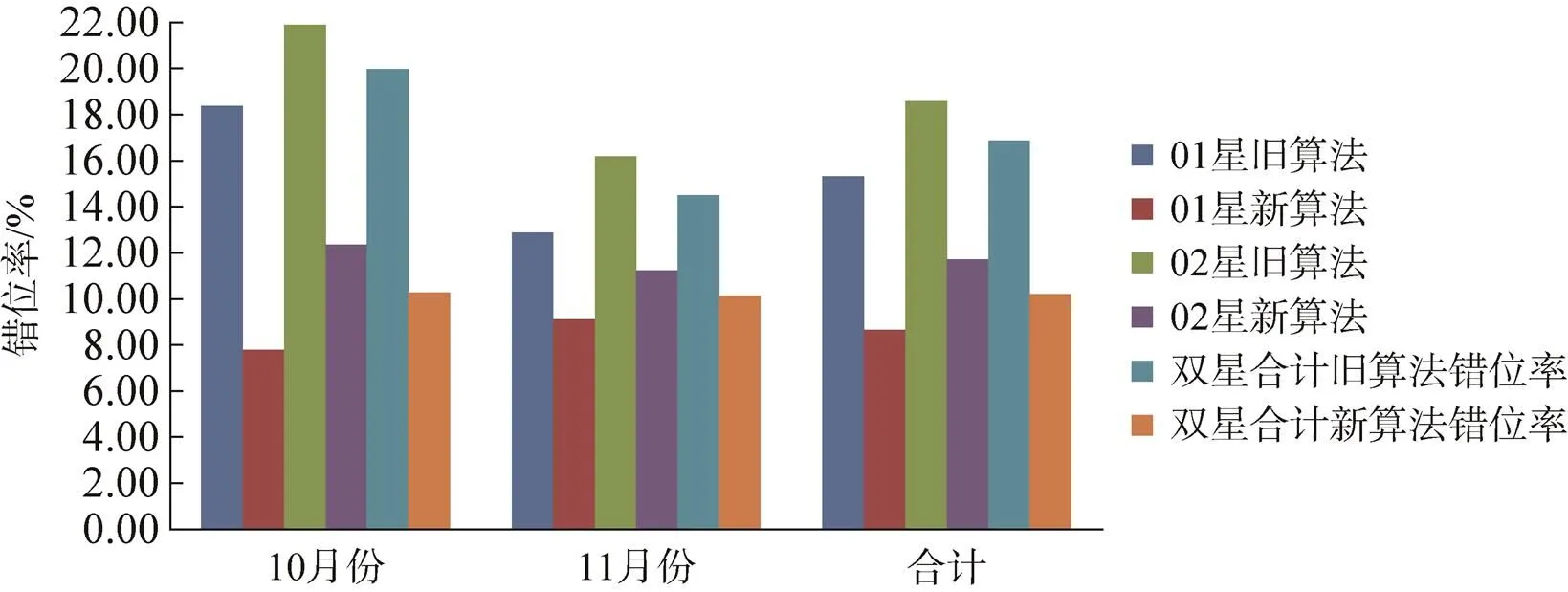
图10 新、旧算法拼接错位率测试结果

从测试结果可以看出，01星、02星、双星合计的新算法较旧算法，错位率降低约7个百分点；另外可以看出新算法01、02星错位率随时间的变化较小，算法性能较旧算法稳定。

4 结束语

“天绘一号”卫星地面预处理系统基于SIFT算法进行2m的分辨率全色相机条带影像拼接，但由于受多种因素的影响，拼接精度不理想。本文在分析各种影响因素的前提下，针对“天绘一号”卫星的成像特点，提出了分段线性拟合，并采用了拼接区域逻辑自适应增强技术，有效提高了“天绘”卫星影像拼接精度。本算法对于云层移动等因素的影响，尚无有效解决办法，目前采用该算法部分产品仍存在拼接错位现象。另外，实践证明，基于物方的虚拟线阵技术能够有效解决“天绘一号”卫星多条带影像拼接精度问题，并得到了工程化应用。笔者下一步将重点对基于像方的拼接技术和基于物方的虚拟线阵拼接技术进行对比研究。

[1] LOWE D G. Distinctive Image Features from Scale-Invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.

[2] 王任享, 王建荣, 王新义, 等. LMCCD相机卫星摄影测量的特性[J]. 测绘科学, 2004, (4): 10-12. WANG Renxiang, WANG Jianrong, WANG Xinyi, et al. The Satellite Photogrammetric Performance of LMCCD Camera[J]. Science of Surveying Mapping, 2004, (4): 15-17. (in Chinese)

[3] 谷口庆治. 数字图像处理基础[M]. 北京: 科学出版社, 2005: 31-55. Taniguchi Yoji. Digital Image Processing Foundation[M]. Science Press, 2005: 31-55. (in Chinese)

[4] 贾世杰, 王鹏翔, 姜海洋, 等. 基于SIFT的图像匹配算法[J]. 大连交通大学学报, 2010, 9, 31(4): 17-21. JIA Shijie, WANG Pengxiang, JIANG Haiyang, et al. Study of Image Matching Algorithm Based on SIFT[J]. Journal of Dalian Jiaotong University, 2010, 31(4): 17-21. (in Chinese)

[5] 曹楠, 王萍. 基于SIFT特征匹配的图像无缝拼接算法[J]. 计算机与运用化学, 2011, 28(2): 242-244. CAO Nan, WANG Ping. Seamless Image Stitching Based on SIFT Feature Matching[J]. Computers and Applied Chemistry, 2011, 28(2): 242-244. (in Chinese)

[6] 徐亚明, 刑诚, 陈晓东. 一种基于拼接线的无人机序列影像拼接方法[J]. 武汉大学学报（信息科学版）, 2011, 36(11): 1265-1269. XU Yaming, XING Cheng, CHEN Xiaodong. A Mosaicking Method for UAV Sequence Images Based on Seam Line[J]. Geomatics and Information Science of Wuhan University, 2011, 36(11): 1265-1269. (in Chinese)

[7] 贾西茜, 催希民, 邱亚辉, 等. 无地面控制点航空图像无缝拼接算法[J]. 影像技术, 2011, 23(4): 34-39. JIA Xiqian, CUI Ximin, QIU yahui, et al. Airphoto Seamless Mosaic Algorithm without Ground Control Point[J]. Image Technology, 2011, 23(4): 34-39. (in Chinese)

[8] YANG H, WANG Q. A Novel Local Feature Descriptor for Image Matching[C]//2008 IEEE International Conference on Multimedia and Expo, Hannover, Germany, 2008: 1405-1408.

[9] LOWE D G. Object Recognition from Local Scale-invariant Features[C]//The 7th International conference on Computer Vision, kerkyra, Greece, 1999.

[10] 刘立, 彭复员, 赵坤, 等. 采用简化SIFT算法实现快速图像匹配[J]. 红外与激光工程, 2008, 37(1): 181-184. LIU Li, PENG Fuyuan, ZHAO Kun, et al. Simplified SIFT Algorithm for Fast Image Matching[J]. Infrared and Laser Engineering, 2008, 37(1): 181-184. (in Chinese)

[11] 吕江安, 于晋, 陈琦. 基于SIFT特征的三线阵CCD影像立体匹配[J]. 航天返回与遥感, 2010, 31(2): 38-45. LYU Jiang’an, YU Jin, CHEN Qi. Stereo Matching of Three-line CCD Imagery Based on SIFT[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(2): 38-45. (in Chinese)

[12] 田国梁, 黄巧林, 何红艳, 等. 遥感卫星图像几何定位精度评估方法浅析[J]. 航天返回与遥感, 2017, 38(5): 106-112. TIAN Guoliang, HUANG Qiaolin, HE Hongyan, et al. Analysis on Geometric Positioning Accuracy Evaluation of Remote Sensing Satellite Image[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(5): 106-112. (in Chinese)

[13] 王欢, 蒋显岚. 4种无人机遥感影像快速拼接方法的试验分析[J]. 测绘与空间地理信息, 2015, 38(8): 117-118. WANG Huan, JIANG Xianlan. Experimental Analysis of 4 Kinds of Remote Sensing Image Mosaic Method for UAV[J]. Geomatics & Spatial Information Technology, 2015, 38(8): 117-118. (in Chinese)

[14] 付云洁. 遥感影像拼接缝消除算法改进研究[J]. 测绘与空间地理信息, 2013, 36(9): 151-153. FU Yunjie. Improving Research on Seamless Mosaicking Algorithm of Remote Sensing Images[J]. Geomatics & Spatial Information Technology, 2013, 36(9): 151-153. (in Chinese)

[15] 李国, 张俊, 龚志辉. 彩色遥感影像色彩保持直接线性增强方法[J]. 地理空间信息, 2012, 10(5): 47-49. LI Guo, ZHANG Jun, GONG Zhihui. Color Retention Direct Linear Enhancement Method for Color Remote Sensing Images[J]. Geospatial Information, 2012, 10(5): 47-49. (in Chinese)

[16] 朱红, 宋伟东, 谭海, 等. 多尺度细节增强的遥感影像超分辨率重建[J]. 测绘学报, 2016, 45(9): 1081-1088. ZHU Hong, SONG Weidong, TAN Hai, et al. Remote Sensing Images Super Resolution Reconstruction Based on Multi-scale Detail Enhancement[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1081-1088. (in Chinese)

（编辑：庞冰）

Technical Study on Improving Stitching Accuracy for TH-1 Satellite Strip Images

CHENG Jiasheng MU Chundi LI Yang JIANG Yanyuan

（Tianhui Satellite Center of China, Beijing 102102, China）

Focal plane of the full color camera on TH-1 satellite consists of eight TDI-CCD elements, which are staggered in upper and lower rows. The eight TDI-CCD strip images are currently stitched by SIFT-based feature point matching algorithm to form one wide-area image. However, due to terrain change, cloud movement and the difference of image contrast, the stitching accuracy is usually low by misplacement, thus reducing the performance of TH-1 image data significantly. In the paper, we focus on analyzing influencing factors of stitching accuracy, and then propose a new method to improve the accuracy by introducing piecewisely linear stitching and logically adaptive image enhancement of the stitching area. The method is validated by real data processing and is currently applied for TH-1strip image stitching, which is effective to solve the stitching parameters inconsistency and low remote sensing image contrast.

Scale-Invariant Feature Transform; piecewisely linear stitching; image enhancement; TH-1 satellite; space remote sensing application

P407.8

A

1009-8518(2018)02-0084-09

10.3969/j.issn.1009-8518.2018.02.010

2017-08-30

程家胜，男，1984年生，2010年获国防科技大学电子科学与工程专业硕士学位，工程师。主要从事航天摄影测量等方面的研究工作。E-mail：chengjias_heng@126.com。