基于深度门控循环单元神经网络的短期风功率预测模型

牛哲文,余泽远，李 波，唐文虎

(华南理工大学 电力学院，广东 广州 510641)

0 引言

风功率预测是风力发电系统中的关键技术，准确地对风电场未来风功率进行预测可以有效地减少和避免风电场对电力系统产生的冲击[1]。因此，风功率预测方法对风力发电的可持续发展起着重要的作用。当前的风功率预测方法可以主要分为物理方法、统计学方法、学习方法以及上述方法的混合，每种方法都有各自适应的时间尺度和数据类型[2]。

物理模型是一种间接预测风功率的方法，它通过风力发电机功率曲线来推算出风功率的预测值[3]。物理模型在长期预测中有着较好的表现，但是由于存在着物理状态到数值状态的转变，以及预测模型参数与以往数据没有直接关联，在短期预测中它的误差会相对较高。

统计模型旨在利用统计学的方法，描绘出风功率的预测值与以往的风功率数据的时间序列之间的关系[4]。常用的统计学方法有时间序列模型、回归分析模型以及卡尔曼滤波模型[5-6]。统计学模型可以有效地解决预测延迟的问题，但长期预测的准确性较低。

学习模型的核心在于通过人工智能算法来构建输入数据与输出数据之间的关系。通过大量数据的训练与学习，使得模型能捕捉到数据中隐含的规律与逻辑，从而做出准确的预测。文献[7]中建立了一种由微分进化优化的支持向量机SVM(Support Vector Machine)模型，并通过小波变换对风速数据进行预处理来得到更加精确的风功率预测结果。文献[8]将云模型与SVM相结合，并使用云变换的方法提取风速数据的特征，从而使预测效果更加准确。文献[9]建立了一种多重支持向量回归模型，并通过增强和声搜索方法来最优化模型中的参数，进而提高短期风功率预测的准确性。但是传统神经网络对长时间序列的处理能力较弱且伴随着梯度消失与过拟合等问题，使得这种方法也难以有较高的准确度。支持向量回归算法虽然能够避免陷入局部最优解，但当处理大规模训练样本时会出现收敛速度慢及难以实施的问题。

随着深度学习[10]的兴起，文献[11]提出了使用长短时间记忆LSTM(Long Short-Term Memory)神经网络的短期负荷预测方法，解决了传统神经网络不能学习长距离依赖关系的问题，使预测准确度上升了一个新的台阶。文献[12]将主成分分析PCA(Principal Component Analysis)法用于分析影响风功率的因素中，并将降维后的输入通过LSTM神经网络进行风功率预测。文献[13]将LSTM仿照自动编码器(autoencoder)的结构，提出了一种序列到序列的学习方法，相比标准的LSTM在多步预测方面做出了改进，但LSTM结构复杂，需要较长的训练和预测时间。

本文提出了一种包含卷积神经网络CNN(Convo-lutional Neural Network)和门控循环单元GRU(Gated Recurrent Unit)[14]的C-GRU深度神经网络模型，其创新点在于：该模型创新地将深度学习理论中深层构架的特征提取优势应用于风功率预测中，一方面利用卷积神经网络来降低数据规模和复杂程度，提升模型整体的泛化与学习能力；另一方面，通过GRU进一步挖掘风电场中不同数据源提供的信息特征，建立多变量时间序列与风功率时间序列之间的非线性关系，解决了传统方法由于风能的高不确定性和噪声干扰而产生的准确度低和建模困难的问题。本文模型利用风电场实例中大量有标签的数据进行训练，优化模型参数，可以有效对风电场风功率进行准确的预测。最后，通过工程实例对该模型进行验证，并与多种预测方法在预测准确度和预测速度方面进行了对比分析。

1 C-GRU深度神经网络

深度学习是机器学习的一个新的分支，它旨在构建更深层的结构来加强模型在海量数据中捕捉隐含特征的能力。与传统的浅层神经网络相比，深度学习有一系列能够进行非线性变换的隐含层，从而能够挑战更加复杂的环境与问题。本文中所使用的卷积神经网络与GRU均是深度学习中的重要方法。

1.1 卷积神经网络

卷积神经网络是一种适合用来处理计算机视觉图像的神经网络[15]，它的核心结构是卷积层。每一层卷积层中都包含一定数量的特征探测器，当输入传入卷积层后，每一个特征探测器都会沿着图像滑动平移进行卷积运算，产生与之对应的特征图谱。而随着卷积层的堆叠，输入中隐含的更深层的特征将会被提取并学习。

图1展示了一个二维卷积层的基本结构，其特征捕捉器是一个3×3维的矩阵，输入矩阵经过特征捕捉器的平移卷积之后得到特征图谱。即对于输入矩阵元素aij，特征图谱M为：

(1)

其中，σ为卷积层的激活函数；ωkl为一个3×3维系数矩阵的元素；ai+k,j+l为卷积层的输入中与ωkl对应相乘的元素，i表示行，j表示列；b为偏置项。每一个系数矩阵只能学习一种单一的特征，故一层中需要多个特征捕捉器，而数据中深层次的特征则需要堆叠更多的卷积层来捕捉。

图1 二维卷积层空间结构Fig.1 Spatial structure of two-dimensional convolutional layer

本文中的输入为时间序列向量，因此将一维的卷积神经网络设置在整个模型的顶部，使之对输入的原始风功率和风速等时间序列进行处理。如图2所示，a1—a7为输入的一维时间序列,F与T分别为2层一维卷积层中的特征捕捉器，max表示最大值池化层，它是一种最常用的池化方法，即对邻域内特征点取最大值。经过池化层后的模型参数将会减少，计算速度得到提升，最终得到特征图谱m1—m3。相比于输入，特征图谱在向量维度上有了一定的减小，并且携带着更加明显的风功率数据特征，这样就可以更好地被之后的网络利用。

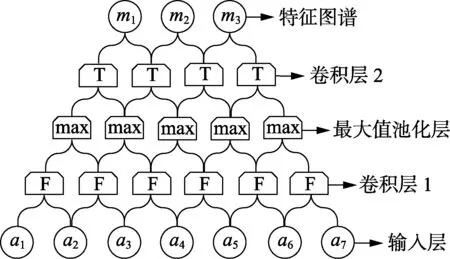
图2 双卷积层的一维卷积神经网络Fig.2 One-dimensional CNN with two convolutional layers

1.2 GRU神经网络

GRU神经网络是循环神经网络RNN(Recur-rent Neural Network)的一种[16]。相比于传统神经网络，RNN能够更好地处理输入为时间序列的任务，因为RNN能够将之前输入产生的影响保留到模型，并共同参与到对下一步输出的计算中。

鉴于RNN的这种特殊结构，它被广泛应用于文本的词句划分以及机器翻译中。理论上，RNN可以利用任意长度的时间序列信息，但是实际中当2个输入之间的步长太大时会很快出现梯度消失或者梯度爆炸现象[17]，从而难以实现。GRU神经网络作为RNN的一种新型变体，它特殊的门结构能够有效地解决长短时间序列上的变化问题。

rt=σ(Wrhht-1+Wrxxt)

(2)

zt=σ(Wzhht-1+Wzxxt)

(3)

图3 GRU内部结构Fig.3 Inner structure of GRU

(4)

(5)

故从上式中可以看出，重置门rt可以控制当前输入xt与之前时刻状态ht-1的结合方式，rt越趋近于0则前一时刻的输出状态所占的比例就越小。更新门zt决定有多少前一时刻的状态信息能够进入现在的时刻，zt越趋近于1，表示当前状态对之前时刻的信息利用得越多。因此，如果将重置门的值设置为1，而更新门的值设置为0，就会得到一个传统的RNN。

GRU可以通过堆叠来形成多层GRU，本文中构建的5层GRU神经网络的结构展开图如图4所示。

图4 5层GRU神经网络结构展开Fig.4 Unrolled architecture of a five-layer GRU neural network

1.3 基于C-GRU神经网络的风功率预测模型

本文采用历史风功率数据和数值天气预报中的风速、风向以及风的经纬分量作为风功率预测模型的输入数据，风功率的预测值作为输出，进行单步预测。模型可以由下式表示：

(6)

图5 C-GRU风功率预测模型结构Fig.5 Structure of wind power forecasting model based on C-GRU

从图5可以看出，C-GRU风功率预测模型由2个主要部分组成，即负责对原始输入数据进行特征提取和降维的卷积神经网络以及负责对处理后的时间序列进行预测的GRU 神经网络。高维的原始输入数据传入卷积神经网络后，通过特征提取器与池化层的处理，形成包含历史风功率数据以及风速数据特征的低维特征图谱。特征图谱作为输入传到GRU神经网络中，GRU神经网络中的重置门与更新门在大量训练中不断地调整自身参数，使它能够从卷积神经网络提取的信息中学习数据间的时间依从关系。最后，在模型的末端加入一个激活函数为线性激活函数的单一神经元L来计算GRU神经网络的预测值，最终整个C-GRU风功率预测模型的输出值即为这个全连接神经元的输出。

对于整个C-GRU风功率预测模型的训练，本文采用了时间反向传播算法，即将循环神经网络按照一定时间步长展开，展开结果可以看作深度的前馈神经网络，进而可以实施标准的反向传播算法。本文中采用Adam[18]算法作为模型梯度的优化算法，相比于传统的随机梯度下降SGD(Stochastic Gradient Descent)法,Adam算法采用自适应动态调整的学习率，一方面能够根据不同的参数选择不同的学习率，另一方面还能够对学习率形成一个动态约束，避免较大的梯度波动。模型中的目标损失函数采用均方误差函数，即：

(7)

其中，Q为训练集中的样本数量；pt为t时刻风电场风功率的真实值。

1.4 dropout技术

本文研究发现，单纯地增加神经网络的深度并不能有效提高模型的预测准确度。由于随着模型网络层数的增加，模型内部参数的数量呈指数型增长，而风功率预测的输入数据结构较为单一且缺乏多样性。经过大量训练之后，模型将倾向于模仿训练数据的特征而缺乏真正的预测，即出现过拟合现象。为了减少模型出现的过拟合现象，本文使用了dropout技术[19]。在训练过程中，dropout 技术按照一定概率将网络中的隐含神经元随机丢弃，即将该神经元的输入与输出置0，使这部分神经元在训练过程中不参与正向与反向传播，但其权值仍保留，如图6所示。图6为一个标准神经网络经过dropout技术处理后的结果，其中被打叉的圆表示被dropout随机丢弃掉的神经元，这样一方面能够有效地减少模型中内部参数的数量，另一方面也相当于变相增加了模型输入数据的多样性，从而在一定程度上减轻了过拟合现象。关于dropout技术和风功率预测模型中的过拟合现象在本文实验部分将进行进一步的讨论。

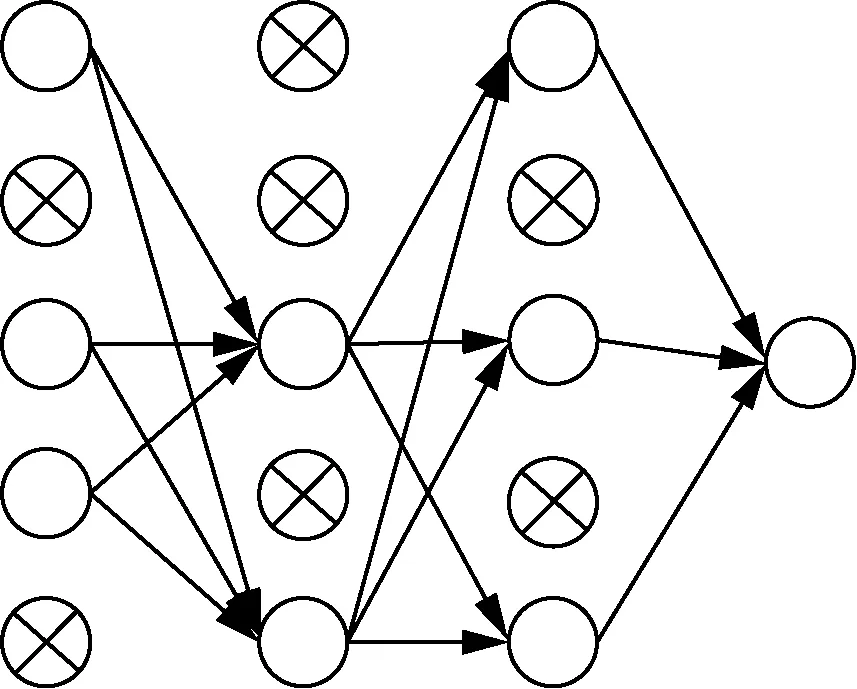
图6 dropout技术示意图Fig.6 Schematic diagram of dropout technique

2 实验算例

2.1 数据集和数据预处理

本文以中国北部的额定功率为49.5MW的某风电场发电机组数据以及数值天气预报中相应的风速预测数据作为研究对象，采样间隔周期为1h。采用从2009年7月1日至2010年11月6日的11834个点的风功率数据作为C-GRU模型的训练集，以2010年11月7日至2010年12月31日的1298个点的数据作为模型的测试集进行试验。

由于测量误差以及风的不确定性，原始数据中充满了噪声信号且有诸多异常值，为了减少测量误差造成的影响，降低由异常值造成的计算误差，采用式(8)来对数值天气预报中的风速风向和风的经纬分量进行标准化处理，并采用风功率的标幺值作为输入，以提高预测的准确率。

(8)

其中，xc为标准化之后的模型输入数据；xs为原始的输入数据；xmax和xmin分别为原始数据的最大值和最小值。

2.2 C-GRU模型预测准确性的评估

本文中采用标准化的平均绝对误差NMAE(Normalized Mean Absolute Error)与标准化的均方根误差NRMSE(Normalized Root Mean Square Error)作为模型准确性的评估标准。NMAE与NRMSE的公式表达如下：

(9)

(10)

2.3 C-GRU模型的训练及实验结果

本节对C-GRU模型进行风功率预测验证。通过实验发现，当模型风功率输入时间序列维度为16时预测结果最好，预测期间设定为4h，即对于某一特定时刻t，采用其前4～19h的真实风功率数据以及t时刻风速、风向和风的经纬分量的数值天气预报预测值作为输入数据预测其4h后时刻的风功率。经过对不同的模型结构及参数进行调参试验，最终模型参数如下。

a. 卷积神经网络：卷积神经网络中包含2层卷积层，第一层中有64个特征探测器(1×4维向量)，第二层中有32个特征探测器(1×3维向量)，它们的激活函数都为ReLu。

b. GRU神经网络：本文中模型包含5层GRU单元，经过试验测试调参，最终设定每一层中的隐含神经元数分别为64、128、64、32和16。

c. 全连接层：一个单一神经元的全连接层作为C-GRU风功率预测模型的输出层，它输出的结果即为t时刻风功率的预测值。

本文研究将C-GRU风功率预测模型与其他风功率预测模型进行比较，如基本BP神经网络模型、基本GRU模型以及SVM模型。以上所有的预测模型都建立在keras库的基础上，以theano为后端通过python语言编写。

C-GRU风功率预测模型的结果如图7所示，图中风功率为标幺值。表1展示了不同模型预测结果的NMAE与NRMSE值。

图7 C-GRU模型的预测结果Fig.7 Forecasting results of C-GRU model

从图7中可以看出，C-GRU风功率预测模型的预测曲线能较好地拟合真实的风功率曲线，具有短时风功率预测的能力。除此之外，由图7(b)可以发现，本文中测试模型存在峰值处预测值低于真实值的情况，这是由于模型输入数据均为历史风功率数据，下一个时刻的预测值取决于之前时刻的真实值，故模型具有一定的预测惯性。因此，当风速波动较大时，模型的整体预测值将偏保守。但C-GRU模型相比于其他模型能够更好地贴合真实的风功率曲线，表现出在更加极端的情形下的风功率预测能力。

表1 多种风功率预测模型在不同风速情况下的误差数据比较Table 1 Errors of different wind power forecasting models under different wind speed situations %

与此同时，在表1所示的误差指标方面，C-GRU模型拥有最小的NMAE值与NRMSE值，即C-GRU模型有最高的预测准确度。在与GRU神经网络的比较中发现，C-GRU模型的准确度有明显提升，这说明卷积神经网络具有很好的数据特征捕捉和数据降维的功能。从不同风速情况下的误差对比中发现，当风速波动较大时，模型的预测误差均会明显增加，但C-GRU模型的误差波动是最小的，在一定程度上证明了C-GRU模型的鲁棒性和适应性。

图8 预测误差随网络层数的变化Fig.8 Forecasting error vs. number of neural network layer

为了探究C-GRU风功率预测模型的预测结果与模型网络深度的关系，本文进行了预测误差与网络层数的敏感度分析实验。如图8所示，在没有施加dropout的情况下，模型在层数为3时达到最好的预测结果(NRMSE为9.64%，NMAE为7.75%)。但随着网络层数的继续增加，模型出现了严重的过拟合现象，当网络层数增加到5时，模型的预测结果比单层网络还要差，这是由于随着网络结构的深化，模型参数变得冗余而复杂，但短期风功率预测的输入数据形式单一且缺乏变化，从而造成的过拟合现象。但当增加dropout后，模型的预测效果随着网络层数的增加并没有衰减，故而在一定程度上减轻了模型的过拟合现象。

为了进一步比较C-GRU模型、LSTM神经网络模型与GRU神经网络模型在短期风功率预测中的效率和性能，本文针对不同的输入时间序列的长度，对三者的预测准确度和训练时间进行了实验比较。为了确保实验的准确性与合理性，三者均采用相同神经元数和隐含层数，并且使用相同的学习率和迭代次数。具体实验结果如表2所示。

表2 不同输入时间序列长度下风功率预测模型误差比较Table 2 Comparison of errors of different wind power forecasting models for different input sequence lengths %

图9 不同输入时间序列长度下单位时期平均训练时间和平均预测时间Fig.9 Average training time and average forecasting time in one epoch for different input time series lengths

图9为不同输入时间序列长度下单位时期的平均训练时间和平均预测时间，从中可以看出，在输入时间序列长度分别为8、16和24的情况下，C-GRU模型和GRU模型的训练时间与预测时间均小于LSTM模型。具体而言，LSTM模型的平均训练时间约为C-GRU模型的1.27倍，而在测试集上的平均预测时间约为C-GRU模型的1.36倍，这说明在短期风功率预测问题上，C-GRU神经网络比LSTM神经网络有更高的效率和更好的性能，这也与GRU网络舍弃LSTM模型中输入门、输出门、遗忘门的复杂结构，而以重置门、更新门代替的简化结构相呼应。对比图9(a)、(b)可以发现，C-GRU模型的训练时间比GRU模型长，但预测速度比GRU模型快，这说明卷积神经网络在处理原始数据的训练过程中，卷积计算会占用较长的时间，而在预测过程中，GRU神经网络使用经过卷积神经网络降维后的数据，预测时间会降低，并且这种现象会随着输入向量维度的增加而愈发明显。

3 结论

针对当前短期风功率预测中存在的准确性及效率不高的问题，本文提出一种新型的C-GRU风功率预测模型，一方面构建了包含双卷积层的一维卷积神经网络，并通过其多层特征捕捉器及最大池化结构，对输入的不确定性时间序列进行有效特征挖掘；另一方面，搭建了5层结构的深度GRU神经网络，利用其独特的门结构，提高了模型对变长度时间序列的信息利用和预测能力，具有工程应用价值。

工程实例分析表明，C-GRU模型相比于传统神经网络模型在预测准确度方面有明显提高。除此之外，在与LSTM模型的比较中发现，C-GRU模型的预测准确度更高，并且平均训练时间是LSTM模型的79%，平均预测时间是LSTM模型的74%。通过对比研究，本文还得出了模型网络深度与预测误差之间的关系以及dropout技术对于模型在训练过程中出现的过拟合现象的影响。笔者下一步研究方向旨在对C-GRU模型的预测误差进行分析与利用，将误差信息传递到模型中以不断地修正模型参数，形成闭环反馈，进一步完善模型的预测准确度。

参考文献：

[1] JUNG J，BROADWATER R P. Current status and future advances for wind speed and power forecasting[J]. Renewable & Sustainable Energy Reviews,2014,31(2)：762-777.

[2] 李文良,卫志农,孙国强,等. 基于改进空间相关法和径向基神经网络的风电场短期风速分时预测模型[J]. 电力自动化设备,2009,29(6)：89-92.

LI Wenliang，WEI Zhinong，SUN Guoqiang，et al. Multi-interval wind speed forecast model based on improved spatial correlation and RBF neural network[J]. Electric Power Automation Equipment，2009，29(6)：89-92.

[3] 张露,卢继平,梅亦蕾,等. 基于不同优化准则的风电功率预测[J]. 电力自动化设备,2015,35(5)：139-145.

ZHANG Lu，LU Jiping，MEI Yilei，et al. Wind power forecasting based on different optimization criterions[J]. Electric Power Automation Equipment，2015，35(5)：139-145.

[4] 欧阳庭辉,查晓明,秦亮,等. 含核函数切换的风电功率短期预测新方法[J]. 电力自动化设备,2016,36(9)：80-86.

OUYANG Tinghui，ZHA Xiaoming，QIN Liang，et al. Short-term wind power prediction based on kernel function switching[J]. Electric Power Automation Equipment，2016，36(9)：80-86.

[5] 甘迪,柯德平,孙元章,等. 考虑爬坡特性的短期风电功率概率预测[J]. 电力自动化设备,2016,36(4)：145-150.

GAN Di，KE Deping，SUN Yuanzhang，et al. Short-term probabilistic wind power forecast considering ramp characteristics[J]. Electric Power Automation Equipment，2016，36(4)：145-150.

[6] 杨建,张利,王明强,等. 计及出力水平影响与自相关性的风电预测误差模拟方法[J]. 电力自动化设备,2017,37(9)：96-102.

YANG Jian，ZHANG Li，WANG Mingqiang，et al. Wind-power forecasting error simulation considering output level and self-correlation[J]. Electric Power Automation Equipment，2017，37(9)：96-102.

[7] 彭春华，刘刚，孙惠娟. 基于小波分解和微分进化支持向量机的风电场风速预测[J]. 电力自动化设备，2012，32(1)：9-13.

PENG Chunhua，LIU Gang，SUN Huijuan. Wind speed forecasting based on wavelet decomposition and differential evolution-support vector machine for wind farms[J]. Electric Power Automation Equipment，2012，32(1)：9-13.

[8] 凌武能,杭乃善,李如琦. 基于云支持向量机模型的短期风电功率预测[J]. 电力自动化设备,2013,33(7)：34-38.

LING Wuneng，HANG Naishan，LI Ruqi. Short-term wind power forecasting based on cloud SVM model[J]. Electric Power Automation Equipment，2013，33(7)：34-38.

[9] HUANG Chaoming，KUO Chunjie,HUANG Yanchang. Short-term wind power forecasting and uncertainty analysis using a hybrid intelligent method[J]. IET Renewable Power Generation,2017，11(5)：678-687.

[10] HINTON G E，SALAKHUTDINOV R. Reducing the dimensionality of data with neural networks[J]. Science,2006，313(5786)：504-507.

[11] ZHENG Jian，XU Cencen. Electric load forecasting in smart grids using long-short-term-memory based recurrent neural network[C]∥2017 51st Annual Conference on Information Sciences and Systems(CISS). [S.l.]：IEEE,2017：1-6.

[12] QU Xiaoyun，KANG Xiaoning，ZHANG Chao，et al. Short-term prediction of wind power based on deep long short-term memory[C]∥2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference. [S.l.]：IEEE，2016：1148-1152.

[13] MARINO D L，AMARASINGHE K，MANIC M. Building energy load forecasting using deep neural networks[C]∥IECON 2016-42nd Annual Conference on Industrial Electronics Society. [S.l.]：IEEE，2016：7046-7051.

[14] HINTON G，LI Deng，DONG Yu，et al. Deep neural networks for acoustic modeling in speech recognition：the shared views of four research groups[J]. IEEE Signal Processing Magazine,2012,29(6)：82-97.

[15] KRIZHEVSKY A，SUTSKEVER I，HINTON G E. ImageNet classification with deep convolutional neural networks[C]∥International Conference on Neural Information Processing Systems. [S.l.]：Curran Associates Inc.，2012：1097-1105.

[16] GRAVES A，MOHAMED A，HINTON G E，et al. Speech recognition with deep recurrent neural networks[C]∥International Conference on Acoustics,Speech，and Signal Processing. [S.l.]：IEEE，2013：6645-6649.

[17] PASCANU R，MIKOLOV T，BENGIO Y，et al. On the difficulty of training recurrent neural networks[C]∥International Conference on Machine Learning. [S.l.]：ICML，2012：1310-1318.

[18] KINGMA D P，BA J. Adam：a method for stochastic optimization[C]∥International Conference on Learning Representations. [S.l.]：ICLR，2015：1-13.

[19] HINTON G E，SRIVASTAVA N，KRIZHEVSKY A，et al. Improving

neural networks by preventing co-adaptation of feature detectors[J]. Computer Science，2012，3(4)：212-223.