基于深度Q学习的强鲁棒性智能发电控制器设计

殷林飞，余 涛

(华南理工大学 电力学院，广东 广州 510640)

0 引言

随着互联电网智能化的发展(即智能电网(smart grids)[1])，参与自动发电控制AGC(Automatic Gene-ration Control)二次调频的机组在不断动态变化，从而逐渐发展了智能发电控制SGC(Smart Generation Control)技术[2]。与此同时，各种新能源和间歇性能源的接入，也给智能电网的控制问题带来了新的挑战，不仅外部扰动不断变化，而且系统内部参数也在不断变化。

对于SGC，依赖于模型的最优策略或算法不能应用于动态模型中，主要在电网环境方面(间歇性新能源的加入[3- 4]、电动汽车的接入给电网带来了较大挑战)[5-6]、电力市场(供求关系、市场实时电价与控制区域之间的博弈)、运行方式(运行方式切换时容易引起频率振荡)、控制策略(不同区域的协调控制问题，要从系统的角度去协调控制，而不是单个区域的控制策略最优)和控制目标方面(同时满足控制性能、经济性和环保等多目标最优)存在问题[2]。针对控制策略问题，目前有强化学习、改进的强化学习(如Q(λ)算法[7]和R(λ)算法[8])、人工神经网络ANN(Artificial Neural Network)[9-12]等算法。虽然这些智能控制算法能应对不同类型的外部扰动，但是当系统内部参数变化时，智能控制算法需要学习的时间较长，因此有学者采用模型参数辨识的方法进行研究[13]。然而该参数辨识一般是应用简单模型建立的参数辨识，当模型复杂、不清楚各个环节的大致模型、无法获取系统有多少环节、有多个参数需要辨识时，该参数辨识方法则有待深入研究。

而在智能控制算法领域，机器学习ML(Machine Learning)近几年成为热点话题，特别是在谷歌公司的人工智能研究团队——深智(DeepMind)[14-15]开展的围棋大赛之后更是成为热点，如文献[15-16]详细介绍了深度学习的分类与发展，文献[14，17-18]分析了深度学习在围棋等游戏中的应用。ML中的ANN可做分类和预测，对其改进后发展了深度强化学习DRL(Deep Reinforcement Learning)[18-20]。不断发展的ML还能解决多智能体系统MAS(Multi-Agent System)的问题，即通过带有深度Q学习DQL(Deep Q Learning)算法的智能体可在不断更新的奖励中寻找最优的动作，从而在整个环境中不断地进行博弈[22]。

因此，本文将ML中的深度神经网络DNN(Deep Neural Network)，融入ML中的Q学习算法框架中，利用训练后的DNN替换Q学习算法中的动作选择机制，提升算法对系统的认知能力，从而首次提出了一种全新架构的DQL算法；并利用所提算法设计智能发电控制器，在由多区域智能体构成的多智能体系统中应用，特别是进行各参数(如类型和干扰等外部扰动，汽轮机的3个关键参数[13,23]、可调容量、爬坡率等内部扰动)可变的大规模仿真。

1 智能发电控制器

1.1 SGC模型

针对高速发展的现代互联电网出现的电网环境方面的变化、电力市场的改革、运行方式的切换、控制策略的改变和控制目标的不同等问题，SGC需在非标称参数下具备最优的控制性能，且SGC具有分布式结构，每个区域利用各自的算法在互联的电网中追求各自的最优控制。在SGC模型中，区域i的SGC模型如图1所示。

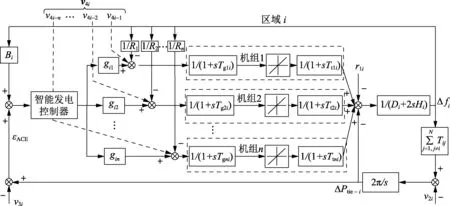
图1 区域i的SGC模型Fig.1 SGC model of Area i

与AGC模型不同的是，控制区域的联络线功率变化不仅包含本地负荷扰动，而且包含本控制区域的基础负荷。图1中基础负荷Ploci由与该地区签订的实时功率供需合同的发电机组来分担[2]。图1中，Δfi为区域i的频率偏差；Bi为区域i的频率偏差系数；ΔPtie-i为区域i的联络线总功率偏差；Ri为区域i的下垂特性系数；Hi为区域i的电力系统等值惯性常数；Di为区域i的电力系统等值阻尼系数；Tgni为区域i第n台发电机组调速器的时间常数；Ttni为区域i第n台发电机组的时间常数；N为控制区域的个数；Tij为区域i和区域j之间的联络线同步系数。该分担由v4i信号来实现。控制区域i的联络线功率变化v2i为：

(1)

而该区域联络线有功功率计划值v3i为：

(2)

其中，gki为第k台发电机机组在区域i的参与因子；ΔPloci、ΔPlocj分别为区域i、j的有功功率差值。根据式(2)可得到任意控制区域的联络线功率偏差为：

ΔPtie-i,error=ΔPtie-i,actual-v3i

(3)

其中，ΔPtie-i,actual为区域i联络线的实时功率。图1中的v4i为外区域发电公司与本区域用电客户签订实时功率供需合同信息，即：

v4i=[v4i-1v4i-2…v4i-n]

(4)

其中，

(5)

在SGC中，发电机组i在SGC模型中发电总功率为：

(6)

1.2 智能发电控制器的控制目标

图1中的智能发电控制器必须控制区域的频率偏差|Δf|尽量小，从而平衡各地区带来的功率误差。因此，智能发电控制器的目的为使频率偏差|Δf|和区域功率误差ACE(Area Control Error)均为0。

为衡量智能发电控制器的控制性能，NERC在1997年提出了统计学性能指标，即CPS指标。εACE则为该区域的功率控制误差(单位为MW)，Δf为频率偏差(单位为Hz)。εACE和Δf越小，则控制性能越优。

首先，定义CPS1指标为：

δCPS1=(2-σCF1)×100%

(7)

其中，εACE，AVE-min为1min ACE的平均值；Bi为控制区域i的频率偏差系数(单位为10MW/Hz)；n0为该统计时间内的分钟数；ε1为互联电网对全年每分钟频率平均偏差的均方根的控制目标值。

CPS2指标定义为：

(8)

其中，Tu、Ts和Tn分别为考核期间不合格时段、总时段和非考核时段。Tu为ACE每10min的平均值大于T10的考核时段数。CPS指标的判断为：

智能发电控制器从电网中采集εACE和Δf，并依据式(7)计算δCPS1指标，以δCPS1和εACE作为输入，以发电机功率指令作为输出。

2 基于DQL的控制器

2.1 Q学习算法

Q学习算法作为“外控制”是不依赖于模型的属于马尔科夫决策过程MDP(Markov Decision Process)的控制算法，它通过不断更新的奖励值来实现动态的最优的控制。Q学习算法的核心是智能体与环境进行交互。对于智能体而言，从环境中获取到状态s和奖励值r，然而事实是奖励值一般由人为设定，包含在智能体中，应为智能体的一部分。Q学习算法中矩阵Q和矩阵P的更新方式为：

Q(s,a)←Q(s,a)+α(R(s,s′,a)+

(9)

(10)

其中，s和s′分别为当前状态和下一时刻状态；β为概率分布因子；概率矩阵P(s,a)的初始值为1/|A|，|A|为动作集中动作的数量，且概率矩阵的范围是P(s,a)∈[0,1]；α为Q学习算法的学习率；γ为折扣因子；R(s,s′,a)为奖励值，奖励值函数依据控制目标而定；a和a′分别为当前时刻的动作和下一时刻的动作值。本文中Q学习算法的智能体的奖励函数为：

(11)

在Q学习算法中，算法稳定性和收敛性有一定的随机性。在概率矩阵选择动作值时，若某动作的概率过大(存在“过学习”)，且其他动作概率很小，此时若未选择概率最大的动作，则会随机地从动作集中选择一个动作进行试错。这种试错会给Q学习的收敛速度带来影响。在试错少量的几个动作之后，能预测到在该情况下选择其他动作带来的影响，而此时DNN则能够实现此预测功能。

2.2 DNN

DNN采用深层次的神经网络作为基础，将多个受限波尔兹曼机RBM(Restricted Boltzmann Machine)堆叠。在训练DNN时，采用无监督的逐层贪心训练方法(逐层进行训练)。在离线训练完成之后，可采用有监督的学习对网络进行边训练边利用；再假定所有可见和隐含单元均为二值变量(只能取0或1)，即i,j,vi,hj∈{0,1}。基于能量定义的RBM系统的能量定义为：

(12)

其中，Wij为链接权重；ai、bj分别为可见元i和隐元j的偏置。此时(v,h)的联合概率分布为：

(13)

(14)

各个可见元的激活概率为：

(15)

2.3 DQL算法

为避免在某状态下多个动作对应的概率相同时Q学习算法的不断试错，加速算法的收敛性，在Q学习算法的框架下加入DNN进行下一时刻动作的预测。设计了DQL算法的框架如附录中图A1所示。

从图A1能看出，DQL的框架和Q学习相似，通过DNN学习加速其对系统的预测能力，通过DNN对动作选择机制的替换，形成DQL算法。图2中展示：在DNN未被训练或预测输出的下一时刻状态不在“理想状态面”附近时，“训练切换开关”应置为“训练DNN”档，其他情况应置为“训练结束”档。理想状态面则由以“当前时刻”状态为x轴，以动作集为y轴，以理想状态构成z轴，平行于oxy的平面构成，“动作选择”则为每次迭代过程中选择理想状态面附近对应的动作作为输出。当DNN无法预测或预测出的状态不在“理想状态面”附近时，智能体自动将“训练切换开关”置为“训练DNN”档。对DQL算法的训练见2.4节。

2.4 基于DQL的控制器的训练与互博弈

对于DQL算法，样本获取极其关键。DQL算法的样本来自于离线训练和在线微调2种方式。离线的静态训练需要在不同的状态s下执行不同的动作a，从而获取下一时刻的状态s′。

离线训练时，对于Q学习、Q(λ)和DQL算法的样本训练，可在某种内部参数情况下采用不同幅值的阶跃输入作为外部扰动进行算法样本训练，为获取不同的“当前时刻”的状态，输入不同的阶跃一段时间(本文算例中取1 000 s)后，待系统稳定在某状态后选择不同的动作进行仿真，获取“下一时刻”的状态作为样本。

在线微调训练时，为加快算法收敛速度，可单独进行单个区域的算法训练。多区域的在线训练为多个基于DQL算法的智能体(或称为控制器)之间的“互博弈”过程，多个基于DQL算法的智能体之间的博弈过程可分多次进行，其流程如图2所示。

图2 多DQL算法控制器的互博弈过程图Fig.2 Game of multi-DQL controller

假定某智能互联大电网共有4个发电控制区域，从图2可看出多个基于DQL算法的控制器之间的互博弈过程为：

Step1 区域{2,3,4}固定选择单独训练得到的最优动作，区域{1}选择不同的动作进行训练；

Step2 区域{1}选择Step1训练得到的最优动作，区域{3,4}固定选择单独训练得到的最优动作，区域{2}选择不同的动作进行训练；

Step3 区域{1,2}选择[Step1,Step2]训练得到的最优动作，区域{4}固定选择单独训练得到的最优动作，区域{3}选择不同的动作进行训练；

Step4 区域{1,2,3}选择[Step1，Step2，Step3]训练得到的最优动作，区域{4}选择不同的动作进行训练；

Step5 区域{1,2,3,4}采用各自区域的DQL算法进行选择。

在训练“当前时刻”的样本时，在“当前时刻”之前的所有时刻的4个区域都用各自的DQL算法进行博弈。

2.5 DQL算法的智能发电控制器设计

针对智能电网的SGC问题，设计了基于DQL算法的智能发电控制器，其结构如图3所示。

图3 基于DQL算法的智能发电控制器Fig.3 Smart generation controller based on DQL algorithm

通过图3可以看出，以DQL算法为基础设计的区域i的智能发电控制器，将εACE和δCPS1指标作为输入、机组出力ΔPmi作为输出。该控制器通过εACE和δCPS1确定所在状态，并更新矩阵Q。此后，若训练未结束，则更新概率矩阵P并训练DNN，否则直接采用DNN进行预测并选择Δf最小对应的动作。针对智能发电控制问题，理想状态面可设定为ε=0.01Hz。

3 仿真算例

所有算例均在CPU为i7-2760 2.4GHz、内存为8 GB的电脑上运行，仿真软件的版本为MATLAB 2016b 9.1.0.441655。

3.1 IEEE标准2区域模型

采用IEEE标准2区域模型作为算例进行仿真，扰动是周期为1200s、幅值为1000MW的正弦扰动。模型中系统的基准容量为5000MW，模型如附录中图A2所示，图中Tg=0.08s，Tt=0.3s，Tp=20s，R=2.4Hz/p.u.，Kp=120Hz/p.u.，T12=0.545s。

DQL、Q学习和Q(λ)算法中的矩阵Q和矩阵P的状态划分为13个，如表1所示。这些算法的动作区间取值为：{-50，-40，-30，-20，-10，0，10，20，30，40，50} MW。

表1 2区域模型DQL、Q学习和Q(λ)算法的状态划分表Table 1 State set of DQL，Q learning，and Q(λ) learning algorithms for two-area model

分别采用4种算法进行仿真，将DQL算法和PID、Q学习和Q(λ)算法进行对比，仿真结果如表2和图4所示。

表2 2区域仿真结果统计表Table 2 Simulative results of two-area model

图4 IEEE标准2区域模型的仿真结果Fig.4 Simulative results of IEEE standard two-area model

表2和图4中的PID、QL、Q(λ)和DQL分别代表PID、Q学习、Q(λ)和DQL控制算法。

其中β是稀疏惩罚项的权重。在学习过程中，通过BP算法对神经网络的W和b的逐步修正，代价函数逐渐被最小化。在此过程中，必须计算隐藏层的每个神经元对输出层误差的贡献。此外，还应该计算代价函数对W和b的偏导数。文献[16]指出，L-BFGS算法在深度学习中训练维度较低的情况下，效果比较好且收敛速度快，运行稳定，因此本文采用L-BFGS算法求解。

从表2可以看出，Q学习、Q(λ)和DQL算法比PID算法的ACE和Δf小，且DQL最小。Q学习、Q(λ)和DQL算法比PID算法的ACE分别小38%、58%和60%。Q学习、Q(λ)和DQL算法比PID算法的Δf分别小35%、54%和58%。

且从图4也可以看出，DQL算法的曲线比其他3种算法的曲线光滑、ACE和Δf小、CPS指标高。因此从仿真结果能看出DQL算法的效果优于其他3种算法。

3.2 以南方电网为背景的4区域模型

为验证所提DQL算法在复杂情况下的鲁棒性，在以南方电网为背景的4区域模型中进行大规模不同参数的数值仿真，在仿真中不仅变换外部扰动的类型和幅值，而且变换系统内部参数，来模拟系统本身的变化，如可调容量模拟丰水期和枯水期，再如汽轮机3个参数(TCH、TRH、TCO)、爬坡率ηGRC和二次调频时延参数Ts等参数的变换。所有参数可选取值如下：外部扰动波形有正弦波、方波、任意波扰动3种；风电接入扰动噪声取0、10%、20%；Ts取8、20、30、35、60、120 s；ηGRC取3、5、8、10 p.u./min；可调容量取1000、500MW；TCH取0.2、0.25、0.3s；TRH取5、6、7、8、9、10s；TCO取0.3、0.4、0.5s。该算例仿真模型如附录中图A3所示。3种外部扰动在噪声为0情况下的波形如图5所示。

图5 不同外部扰动曲线图Fig.5 Curves of different external disturbances

可以看出，选择不同系统内部和外部参数时，共有3×3×6×4×2×3×6×3=23328种组合，每种不同参数组合的模型需在线仿真1 200 s，共需要23328×1200=27993600 (s)，即324d。每种组合需测试4种算法(PID、Q学习、Q(λ)和DQL算法)，共324×4=1 296 (d)。

该算例中DQL、Q学习和Q(λ)算法中的矩阵Q和矩阵P的状态也划分为13个，如表3所示。这些算法的动作取值为：{-500，-400，-300，-200，-100，0，100，200，300，400，500}MW。

表3 4区域模型DQL、Q学习和Q(λ)算法的状态划分表Table 3 State set of DQL，Q learning and Q(λ) learning algorithms for four-area model

本算例中的Q学习、Q(λ)算法是在每种变参数的组合中单独训练的。而DQL算法在某一种参数(参数如下：任意波扰动，噪声为0，Ts=30 s，ηGRC=5p.u./min，可调容量为1000MW，TCH=0.25s，TRH=8s，TCO=0.3s)下进行训练，在其他参数的情况下直接应用。

最后在模型中的4个区域都应用上述4种算法进行数值仿真，其结果统计如图6 — 8和表4所示(由于篇幅原因，只展示了不同扰动类型下其他不同参数组合的统计结果，其他不同参数组合的仿真结果与表4趋势一致)。

图6 4区域仿真结果统计箱形图Fig.6 Statistics for four-area model(box chart)

从图6和图7可以看出：在系统参数和外部参数不断变化的过程中，PID算法、Q学习和Q(λ)算法得到的Δf和εACE并非在每个区域都小，而DQL算法并非追求单一的CPS指标，而是满足综合CPS指标的情况下，尽量使得Δf最小；除区域3外，εACE和Δf以DQL算法最小，δCPS以DQL算法为最大。

图7 4区域仿真结果统计蜘蛛网图Fig.7 Statistics for four-area model(spider chart)

图8 4区域仿真结果状态分布图(区域1)Fig.8 Simulative results distribution of four-area model(Area 1)

扰动类型算法δCPS1/%δCPS2/%εACE/MWΔf/HzδCPS/%方波PID198.69681006.9987230.01375266.36QL199.88721003.4362840.037363100Q(λ)199.86311003.3895660.036728100DQL196.833810037.353040.035156100正弦波PID199.31011004.3674400.00757456.70QL199.89601003.3453310.029233100Q(λ)199.95651003.3030470.025464100DQL197.348710037.036550.034586100任意波PID198.96281005.5986480.01051672.97QL199.55621003.3934250.056542100Q(λ)199.55631003.3413600.053409100DQL197.015110037.225230.035218100总PID198.98991005.654930.01061465.35QL199.77981003.391680.041046100Q(λ)199.79191003.344650.038534100DQL197.065810037.204940.034987100

图8的状态分布图是分别以εACE、Δf和δCPS为x、y和z坐标轴绘出的区域1的性能分布图，可以看出，DQL算法的控制性能优于其他3种算法控制性能(DQL算法的δCPS高，且εACE和Δf低)。

因此从该仿真结果可以看出，与PID算法、Q学习和Q(λ)算法相比，DQL算法的控制性能最优、算法更稳定，由其设计的控制器鲁棒性更强。

4 结论

针对智能电网中的SGC问题，提出了DQL算法，并设计了基于DQL算法的智能发电控制器，最后在IEEE标准2区域和以复杂南方电网为背景的大规模不同参数4区域模型(采用了23328种不同模型参数)中进行数值仿真。所提DQL算法具有以下优点：

a. 与PID、Q学习和Q(λ)算法相比，所提DQL算法控制效果最优，验证了其解决SGC问题具有可行性和有效性；

b. 在大规模仿真实验中，基于所提DQL算法设计的智能发电控制器具有最强鲁棒性；

c. 所提DQL算法在多智能体系统中能够进行互博弈，从而探索最优控制过程。

在下一步工作中，将利用所提DQL算法设计更多电力系统控制器，如自动电压控制器、电力系统稳定控制器等。

附录见本刊网络版(http：∥www.epae.cn)。

参考文献：

[1] KEYHANI A，CHATTERJEE A. Automatic generation control structure for smart power grids[J]. IEEE Transac-tions on Smart Grid，2012，3(3)：1310-1316.

[2] 王怀智. 智能发电控制的多目标优化策略及其均衡强化学习理论[D]. 广州：华南理工大学，2015.

WANG Huaizhi. Multi-objective strategy for smart generation control and equilibrium reinforcement learning theory[D]. Guangzhou：South China University of Technology，2015.

[3] 陈丽娟,姜宇轩,汪春. 改善电厂调频性能的储能策略研究和容量配置[J]. 电力自动化设备,2017,37(8)：52-59.

CHEN Lijuan，JIANG Yuxuan，WANG Chun. Strategy and capacity of energy storage for improving AGC performance of power plant[J]. Electric Power Automation Equipment，2017,37(8)：52-59.

[4] 李本新,韩学山,刘国静,等. 风电与储能系统互补下的火电机组组合[J]. 电力自动化设备,2017,37(7)：32-37，54.

LI Benxing，HAN Xueshan，LIU Guojing，et al. Thermal unit commitment with complementary wind power and energy storage system[J]. Electric Power Automation Equipment，2017,37(7)：32-37，54.

[5] 李清,张孝顺,余涛,等. 电动汽车充换电站参与电网AGC功率分配的成本一致性算法[J]. 电力自动化设备,2018,38(3)：80-87,95.

LI Qing，ZHANG Xiaoshun，YU Tao，et al. Cost consensus algorithm of electric vehicle charging station participating in AGC power allocation of grid[J]. Electric Power Automation Equipment，2018,38(3)：80-87,95.

[6] 程军. 风光互补智能控制系统的设计与实现[D]. 合肥：中国科学技术大学，2009.

CHENG Jun. Design and realization of hybrid wind/photovoltaic intelligent generation system[D]. Hefei：University of Science and Technology of China，2009.

[7] YU T，WANG H Z，ZHOU B，et al. Multiagent correlated equilibrium Q(λ) learning for coordinated smart generation control of interconnected power grids[J]. IEEE Transactions on Power Systems，2015,30(4)：1669-1679.

[8] 余涛，梁海华，周斌. 基于R(λ)学习的孤岛微电网智能发电控制[J]. 电力系统保护与控制，2012,40(13)：7-13.

YU Tao，LIANG Haihua，ZHOU Bin. Smart power generation control for microgrids islanded operation based on R(λ) learning[J]. Power System Protection and Control，2012,40(13)：7-13.

[9] ZEYNELGIL H L，DEMIROREN A，SENGOR N S. The application of ANN technique to automatic generation control for multiarea power system[J]. International Journal of Electrical Power & Energy Systems，2002，24(5)：345-354.

[10] CHEN D，KUMAR S，YORK M，et al. Smart Automatic Generation Control[C]∥Power and Energy Society General Meeting. San Diego,California，USA：IEEE，2012：1-7.

[11] SAIKIA L C，MISHRA S，SINHA N，et al. Automatic generation control of a multi area hydrothermal system using reinforced learning neural network controller[J]. International Journal of Electrical Power & Energy Systems，2011，33(4)：1101-1108.

[12] IMTHIAS T P，NAGENDRA P S，SASTRY P S. A neural network based reinforcement learning controller for automatic generation control[C]∥National Power Systems Conference，NPSC2002. Hyderabad，India：Indian Institute of Technology，2002：161-165.

[13] 盛锴,江效龙,魏乐. 基于功率响应的汽轮机调节系统模型参数辨识方法研究[J]. 电力系统保护与控制,2016,44(12)：100-107.

SHENG Kai，JIANG Xiaolong，WEI Le. Research on parameter identification of turbine governing system based on power response characteristics[J]. Power System Protection and Control,2016，44(12)：100-107.

[14] MNIH V，KAVUKCUOGLU K，SILVER D，et al. Human-level con-trol through deep reinforcement learning[J]. Nature，2015，518(7540)：529-533.

[15] 赵冬斌,邵坤,朱圆恒，等. 深度强化学习综述：兼论计算机围棋的发展[J]. 控制理论与应用,2016,33(6)：701-717.

ZHAO Dongbin，SHAO Kun，ZHU Yuanheng，et al. Review of deep reinforcement learning and discussions on the development of computer go[J]. Control Theory & Applications,2016,33(6)：701-717.

[16] 尹宝才，王文通，王立春. 深度学习研究综述[J]. 北京工业大学学报，2015(1)：48-59.

YIN Baocai，WANG Wentong，WANG Lichun. Review of deep lear-ning[J]. Journal of Beijing University of Technology，2015(1)：48-59.

[17] 陈兴国，俞扬. 强化学习及其在电脑围棋中的应用[J]. 自动化学报，2016，42(5)：685-695.

CHEN Xingguo，YU Yang. Reinforcement learning and its application to the game of go[J]. Acta Automatica Sinica，2016，42(5)：685-695.

[18] PENG X B，BERSETH G，MICHIEL V D P. Terrain-adaptive locomotion skills using deep reinforcement learning[J]. Acm Transactions on Graphics，2016，35(4)：81.

[19] DENG Y，BAO F，KONG Y，et al. Deep direct reinforcement learning for financial signal representation and trading[J]. IEEE Transac-tions on Neural Networks & Learning Systems，2017，28(3)：653-664.

[20] LI L，LÜ Y，WANG F Y. Traffic signal timing via deep reinforcement learning[J]. IEEE/CAA Journal of Automatica Sinica，2016，3(3)：247-254.

[21] JR G V D L C，DU Y，IRWIN J，et al. Initial progress in transfer for deep reinforcement learning algorithms[C]∥Deep Reinforcement Learning：Frontiers and Challenges. New York，USA：[s.n.],2016:1-6.

[22] 郑闻成. 基于JADE的多智能体动态博弈自动发电控制仿真平台研究[D]. 广州：华南理工大学，2014.

ZHENG Wencheng. Research on multiagent simulation platform for AGC Based on JADE[D]. Guangzhou：South China University of Technology,2014.

[23] 许天宁. 汽轮机电液调节系统模型参数辨识研究[D]. 吉林：吉林大学，2015.

XU Tianning. Research on model and parameter identification of the turbine DEH system[D]. Jilin：Jilin University，2015.