基于小波分析的水稻生育期气象因子对产量的影响

李琳琳，王贺然 ，李 晶 ，宋晓巍 ，刘 青 ，李雨鸿 ，王 婷 ，胡春丽 ，黄 岩 ，张晓月 ，王 莹 ，张 琪 ，周 斌

（1.辽宁省气象科学研究所，辽宁沈阳110161；2.沈阳市气象局，辽宁沈阳110168）

水稻是辽宁省重要的粮食作物，截止2016年，辽宁省种植水稻面积约56.25万hm2。辽宁地区由于气候原因主要以种植水稻为主，通过多年的实践和发展，技术和品种不断完善，品质亦有很大的改观。光、温、水是影响水稻生长发育的重要气象因素，在水稻的某个发育期内，这些气象要素中的一个因素或者几个因素对产量会起到关键的作用，因此研究水稻产量及气象因子的时序变化特征和其相互影响关系显得尤为重要。

国内学者关于气候变化对农业生产影响方面的研究也较多。早期陈柏林在气候对常德地区水稻产量的影响研究中，对水稻主产区的主要气候因子进行了定量统计分析，认为秋季低温是影响晚稻产量的主要气候因子，并提出划分晚稻气候类型的标准[1]。涂悦贤从气象角度分析了水稻产量变动与气象因子的关系，探讨了近百年来广东气候变动的趋势，提出了实现水稻稳产高产的对策[2]。许信旺等利用传统的统计分析方法研究了气候的变化，并对水稻生产进行了时空动态分析，揭示了气候变化对水稻生长期生产的巨大影响，并提出应调整市场机制及作物布局以加强对极端气象灾害的防范[3]。张宇等则利用数值模拟的方法研究气候对我国水稻生产可能会产生的影响[4]。

对于气象因子对水稻产量的影响关系的研究，以往多采用传统的多元线性回归等统计分析方法，但该方法不能直接地分析气象因子与水稻产量的时序关系[5]。所以本研究利用1986—2015年间辽宁省水稻产量数据和同时期的气象数据，研究气象因素对水稻产量的影响，提取水稻气象产量及同期时序气象因子进行连续小波分析，研究水稻气象产量及其与各气象因子的时序变化特征；利用相干小波和交叉小波分析，研究水稻产量与各气象因子的相互影响关系，为水稻产量的定量化预报提供依据。

1 资料与方法

1.1 资料来源

选取辽中、新民、普兰店、大洼等共32个水稻主产县（市）为水稻研究区域。水稻产量资料来自辽宁省统计年鉴；水稻生育期资料来自农业气象观测报表；气象资料来自辽宁省气象局，选取年份为1986—2015年，包括日平均气温、日照时数、日最低气温、日最高气温、昼夜温差、水汽压、总风速和相对湿度。

1.2 数据处理

1.2.1 产量资料处理。粮食作物产量一般可以分解为趋势产量、气象产量和随机产量[6]，即

式中，y表示为实际产量，ya表示趋势产量，yb表示气象产量，σ表示为随机产量，其中随机产量一般可以忽略不计。

1.2.2 气象资料处理。气象因子包括日平均气温、日照时数、日最低气温、日最高气温、昼夜温差、水汽压、总风速和相对湿度。将其按照辽宁省水稻生育期各阶段，分为分蘖期（6月中旬至7月上旬）、孕穗期（7月中旬至8月上旬）和开花结实期（8月中旬），分别进行数据处理。

1.3 研究方法

1.3.1 连续小波。连续小波变换（continue wavelet transform，简写为 CWT）[7]。Morlet复数小波函数表示为：

式中，η为自变量；ω0为无量纲频率,取值ω0＝6。离散小波变换形式为：

式中，Wf（α，b） 为小波变换系数，ψ*表示复共轭函数，a为尺度因子（小波周期长度），b为时间平移因子，δt为采样时间间隔[5,7,13-14]。

1.3.2 相干小波和交叉小波。相干小波和交叉小波方法用来研究2个或多个时间序列多尺度相互关系。交叉小波变换是判断2种信号不同时间序列变化周期在时间区域中的相关性。交叉小波谱可用来表示2个时间序列在时频空间中的能量共振和协方差分布规律，揭示了2个序列不同尺度上、不同时段的相关性和一致性。相干小波可以弥补交叉小波变换的不足，并可度量两者在低能量区的相关性[8-9]。

本研究运用红色噪音标准谱对连续交叉小波功率谱和小波相干谱进行显著性检验。连续小波、交叉小波和相干小波分析计算程序来自科罗拉多大学波尔德分校大气和海洋科学网站（http://paos.colorado.edu/research/wavelets/）。

2 结果与分析

2.1 水稻产量分析

水稻气象产量连续小波分析。图1中，辽宁省水稻气象产量在1987—2001年存在5～8年的显著周期；在2～3年显著周期尺度上，较强的能量发生在1991—1997年；自2001年之后，水稻在频率上的能量强弱则分布不显著。这种周期变化表明，水稻气象产量的变化频率在减慢，气象产量连续丰年的周期在变长。

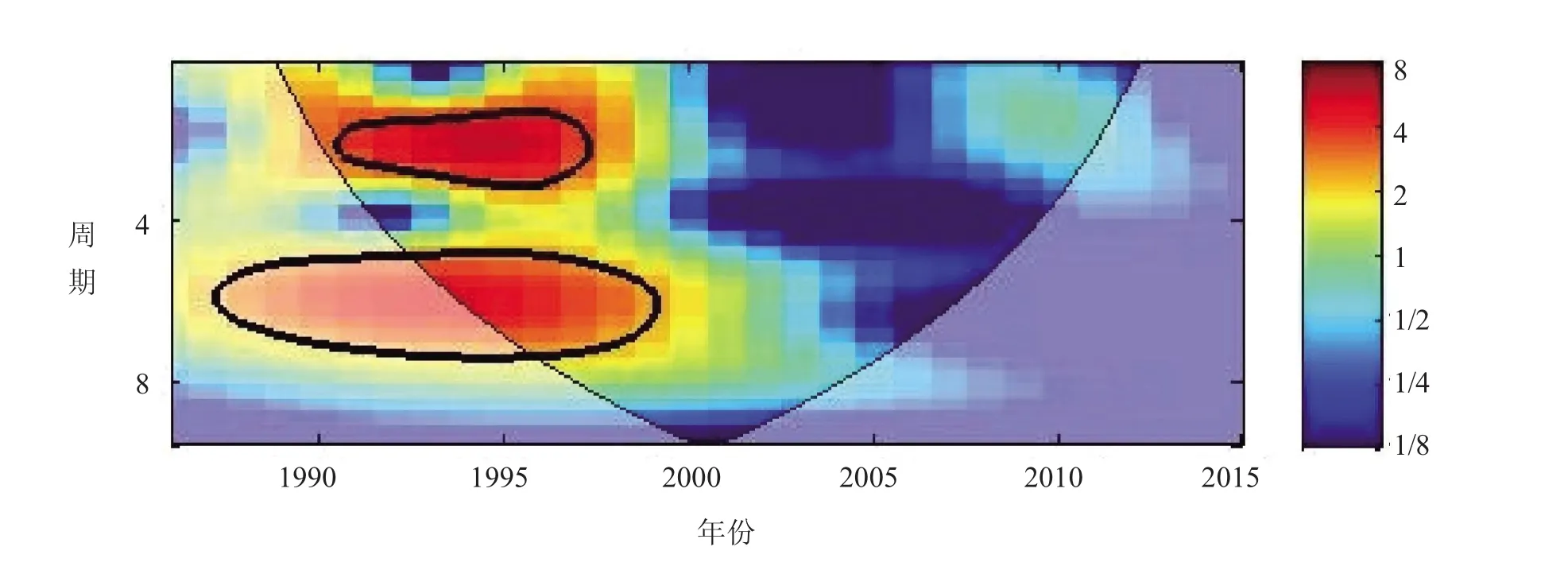
图1 辽宁省1986—2015年水稻气象产量连续小波功率谱

2.2 气象因子的连续小波分析

2.2.1 水稻分蘖期气象因子连续小波分析。由图2可知，累计降水量在2000—2002年存在1年的显著周期；日平均气温在1993—1999年有2～3年的显著周期；累计日照时数在1997—2001年有1～2年的显著周期；日最低气温在1993—2003年存在2～4年的显著周期；昼夜温差在1993—2003年存在1～4年的显著周期；日最高气温在1995—1996年存在1～2年的显著周期；相对湿度在1997—2000年存在1～2年的显著周期；总风速在1991—1996年存在3～4年的显著周期。

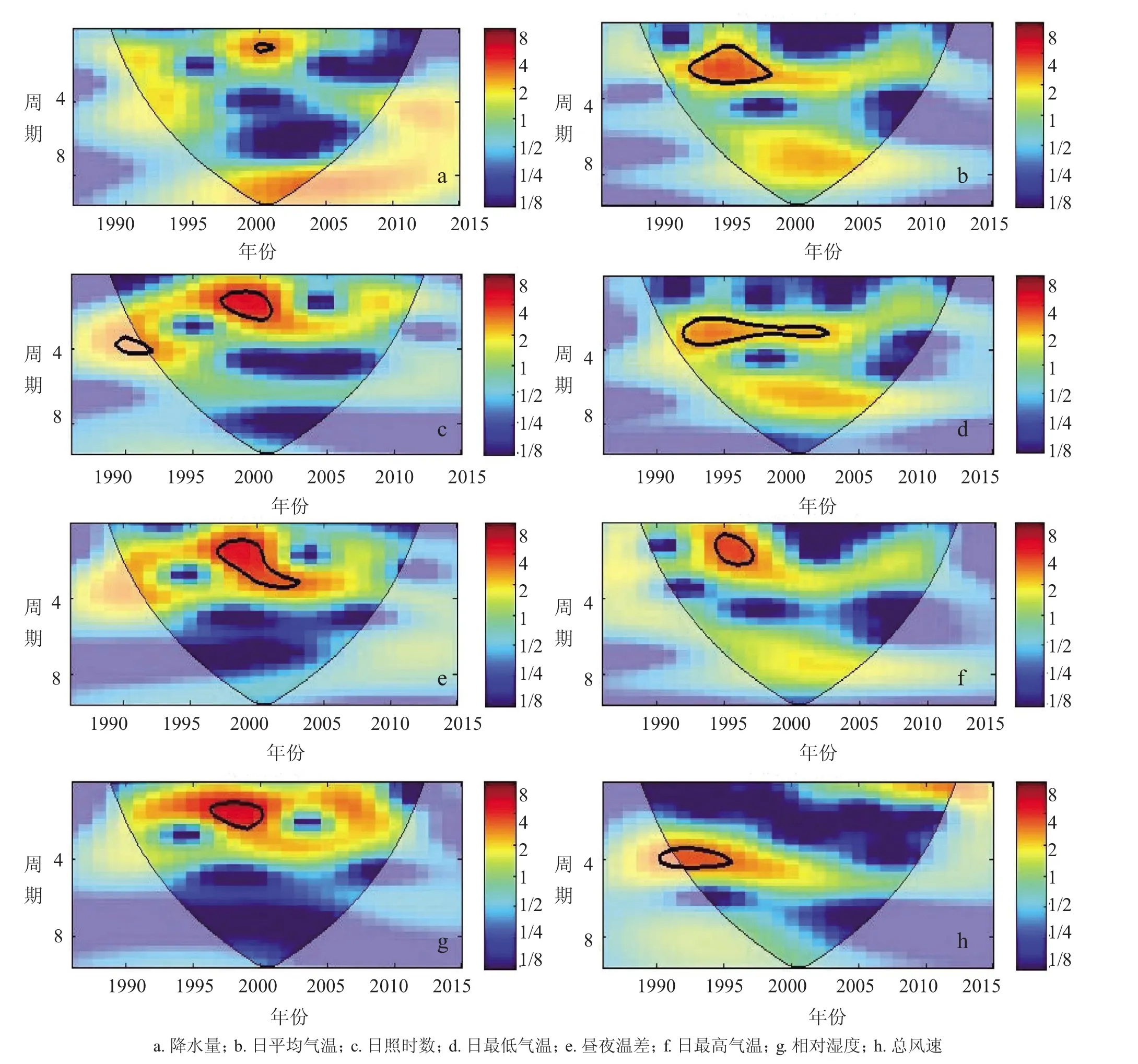
图2 水稻分蘖期降水量、日平均气温、日照、日最低气温、昼夜温差、日最高气温、相对湿度、风速的连续小波功率谱

2.2.2 水稻孕穗期气象因子连续小波分析。由图3可知，分蘖期累计降水未通过0.05显著水平的红噪音标准谱检验；日平均气温在1994—1996年有1～2年的显著周期；累计日照时数在1997—1998年有0～1年的显著周期；日最低气温在2004—2006年存在5～6年的弱显著周期；日最高气温在1994—1999年存在0～3年的显著周期；昼夜温差在1996—1998年存在0～2年的显著周期；相对湿度在1996—1997年存在0～1年的显著周期；总风速在1994—2000年存在2～3年的显著周期。

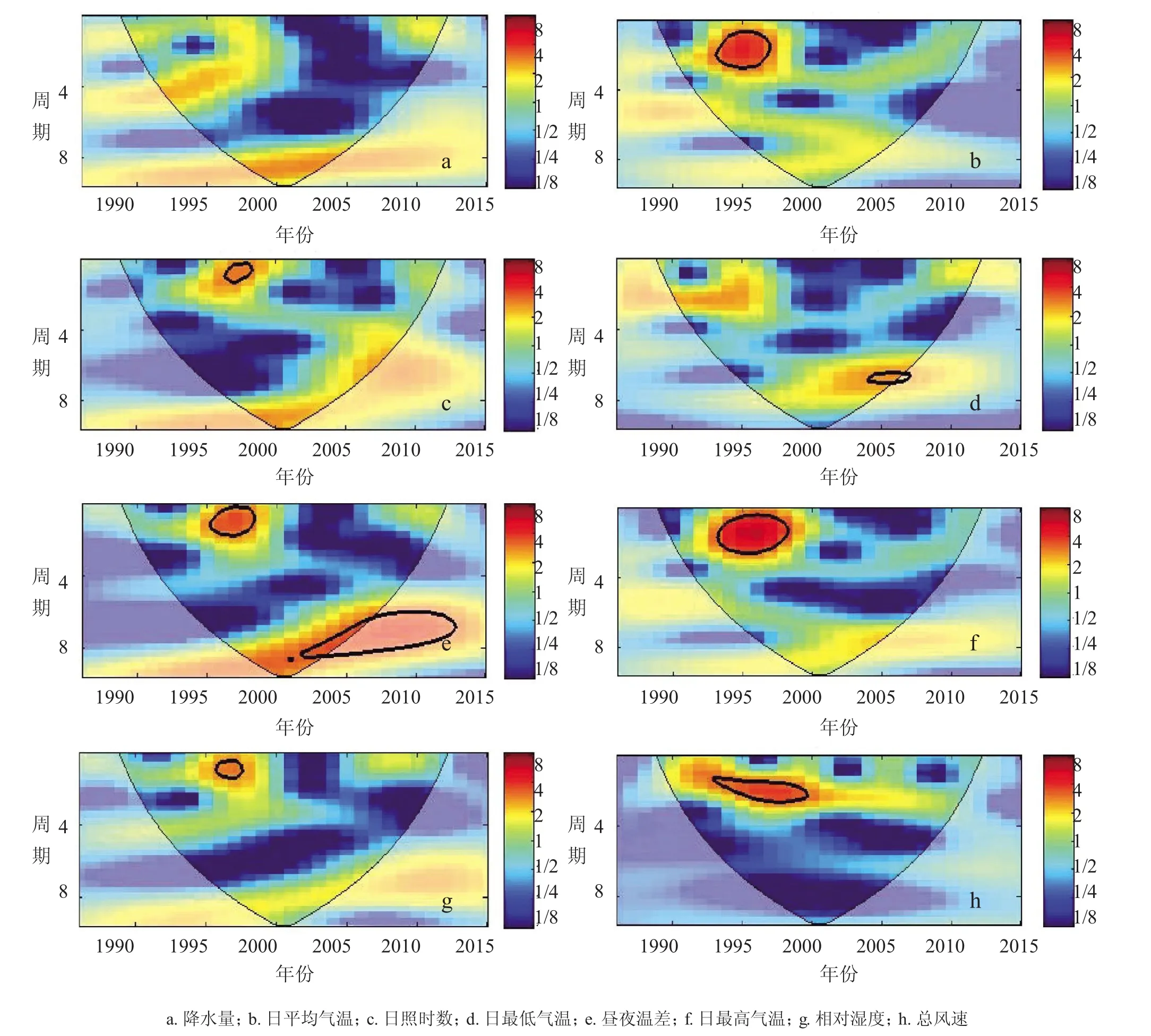
图3 水稻孕穗期降水量、日平均气温、日照、日最低气温、昼夜温差、日最高气温、相对湿度、风速的连续小波功率谱

2.2.3 水稻开花结实期气象因子连续小波分析。由图4可知，分蘖期累计降水和总风速均未通过0.05显著水平的红噪音标准谱检验；日平均气温在1989—1995年有2～3年的显著周期；日最低气温在1988—1993年存在2～3年的弱显著周期；日最高气温在1991—1998年存在2～3年的显著周期；昼夜温差在2003—2008年存在5～6年的显著周期；累计日照时数在2005—2006年有0～1年的显著周期，在2000—2007年存在5～6年的显著周期；相对湿度在2006—2010年存在2～3年的显著周期。

2.3 水稻气象产量与气象因子的交叉小波与相干小波分析

2.3.1 水稻气象产量与分蘖期气象因子的交叉小波与相干小波。由图5、图6可知，在分蘖期，水稻气象产量与累计降水量在1990—1994年存在1～2年共振周期，气象产量变化位相落后于累计降水量90°；气象产量与日最高气温在1993—1998年存在2～3年共振周期，气象产量变化位相均落后于日最高气温90°；气象产量与日平均气温在1990—1998年存在2～3年共振周期，气象产量变化位相分别落后于日平均气温90°；气象产量与累计日照时数在1990—2000年存在1～2年共振周期，气象产量与累计日照时数反位相。气象产量与日最低气温在1991—1997年存在3～4年共振周期，气象产量变化位相落后于日最低气温90°；气象产量与昼夜温差在1990—1999年存在1～2年共振周期，气象产量变化位相落后于昼夜温差90°；气象产量与相对湿度在1991—1999年存在1～2年共振周期，气象产量变化位相比昼夜温差提前90°；气象产量与总风速在1993—1996年存在3～5年共振周期，气象产量变化位相落后于总风速90°。

图4 水稻开花结实期降水量、日平均气温、日照、日最低气温、昼夜温差、日最高气温、相对湿度、风速的连续小波功率谱

在低能量区，气象产量与降水量、相对湿度及总风速没有通过95%置信水平的显著周期；气象产量与日最高气温、日平均气温、累计日照时数、日最低气温及昼夜温差间周期显著不同，且位相较乱。

2.3.2 水稻气象产量与孕穗期交叉小波与相干小波。图7、图8分别为水稻气象产量与孕穗期气象因子交叉小波变换和相干小波谱。由图7可知，在孕穗期，水稻气象产量与累计降水量在1994—1997年存在3～4年共振周期，二者反位相；气象产量与日最高气温在1991—1998年存在1～3年共振周期。气象产量与日平均气温在1991—1998年存在2～3年共振周期，气象产量变化位相分别落后于日平均气温90°；气象产量与累计日照时数在1993—1997年存在1～3年共振周期，气象产量变化位相落后于累计日照时数90°；气象产量与日最低气温在1989—1996年存在2～3年共振周期，气象产量变化位落后于日最低气温90°；气象产量与昼夜温差在1993—1998年存在1～3年共振周期，气象产量变化位相落后于昼夜温差90°；气象产量与相对湿度在1993—1997年存在1～2年共振周期，气象产量变化位相比昼夜温差提前90°；气象产量与总风速在1990—1999年存在2～5年共振周期，二者反位相。

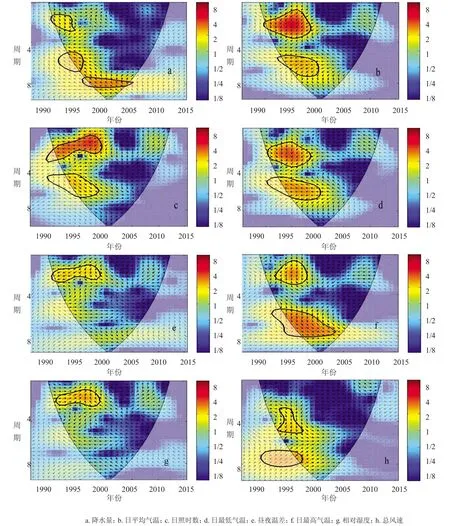
图5 水稻气象产量与分蘖期气象因子交叉小波功率谱

图6 水稻气象产量与分蘖期气象因子相干小波谱

在低能量区，气象产量与降水量、昼夜温差及相对湿度没有通过95%置信水平的显著周期；气象产量与日最高气温、日平均气温和日最低气温间显著周期基本一致，气象产量变化位相落后气象因子90°；气象产量与累计日照和总风速显著周期基本一致，二者位相相反。

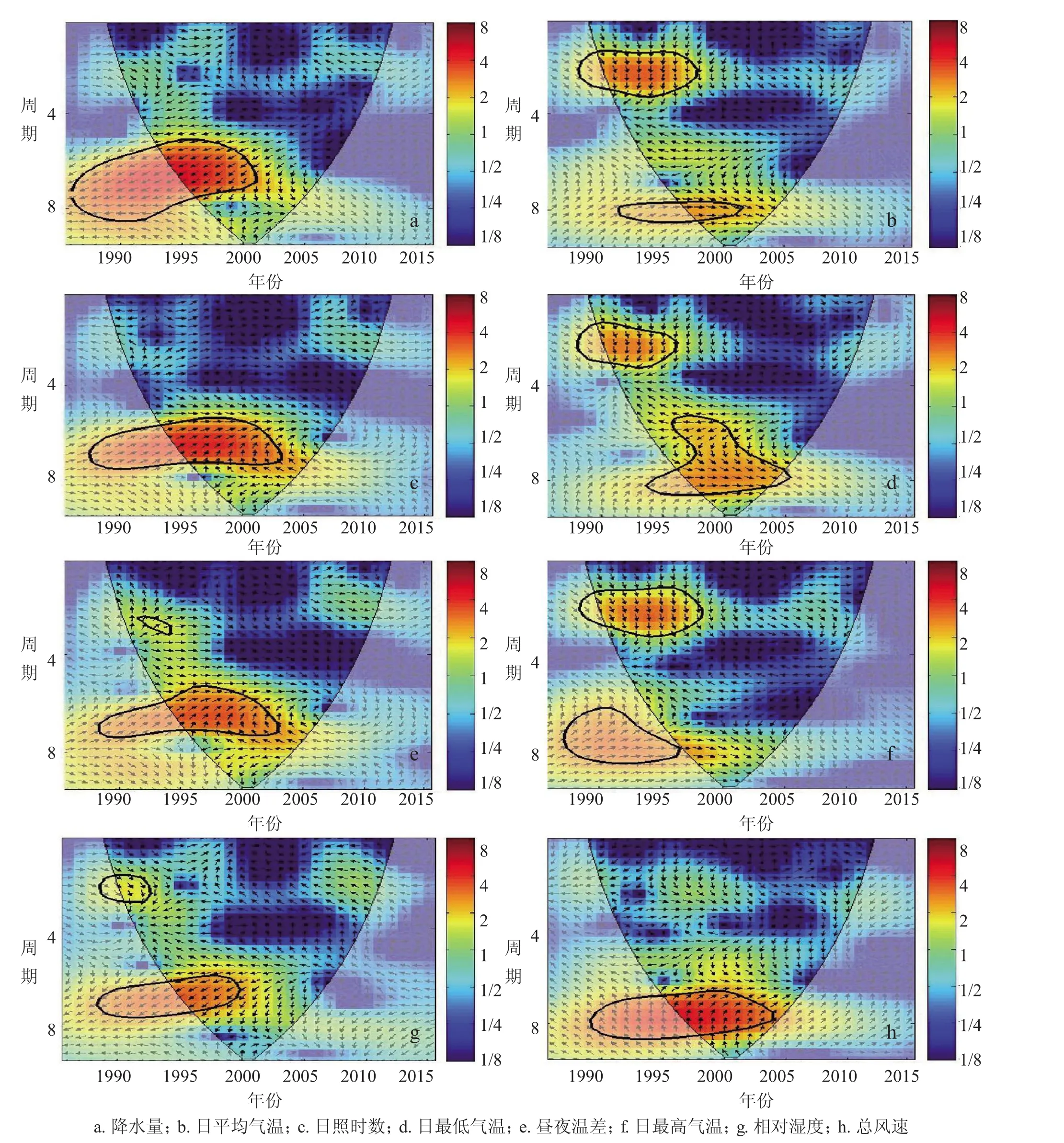
2.3.3 水稻气象产量与开花结实期交叉小波与相干小波。图9、图10分别为水稻气象产量与开花结实期气象因子交叉小波变换和相干小波谱，在开花结实期，水稻气象产量与累计降水量、累计日照时数、相对湿度和总风速大部分共振周期处于影响锥曲线外侧，故认为其无共振周期；气象产量与日最高气温在1989—1998年存在1～3年共振周期，气象产量变化位相落后于日最高气温90°；气象产量与日平均气温在1988—1998年存在2～3年共振周期，气象产量变化位相分别落后于日平均气温90°；气象产量与日最低气温在1988—1996年存在2～3年共振周期，气象产量变化位相落后于日最低气温90°；气象产量与昼夜温差在1992—1994年存在2年共振周期，气象产量变化位相提前于昼夜温差90°。

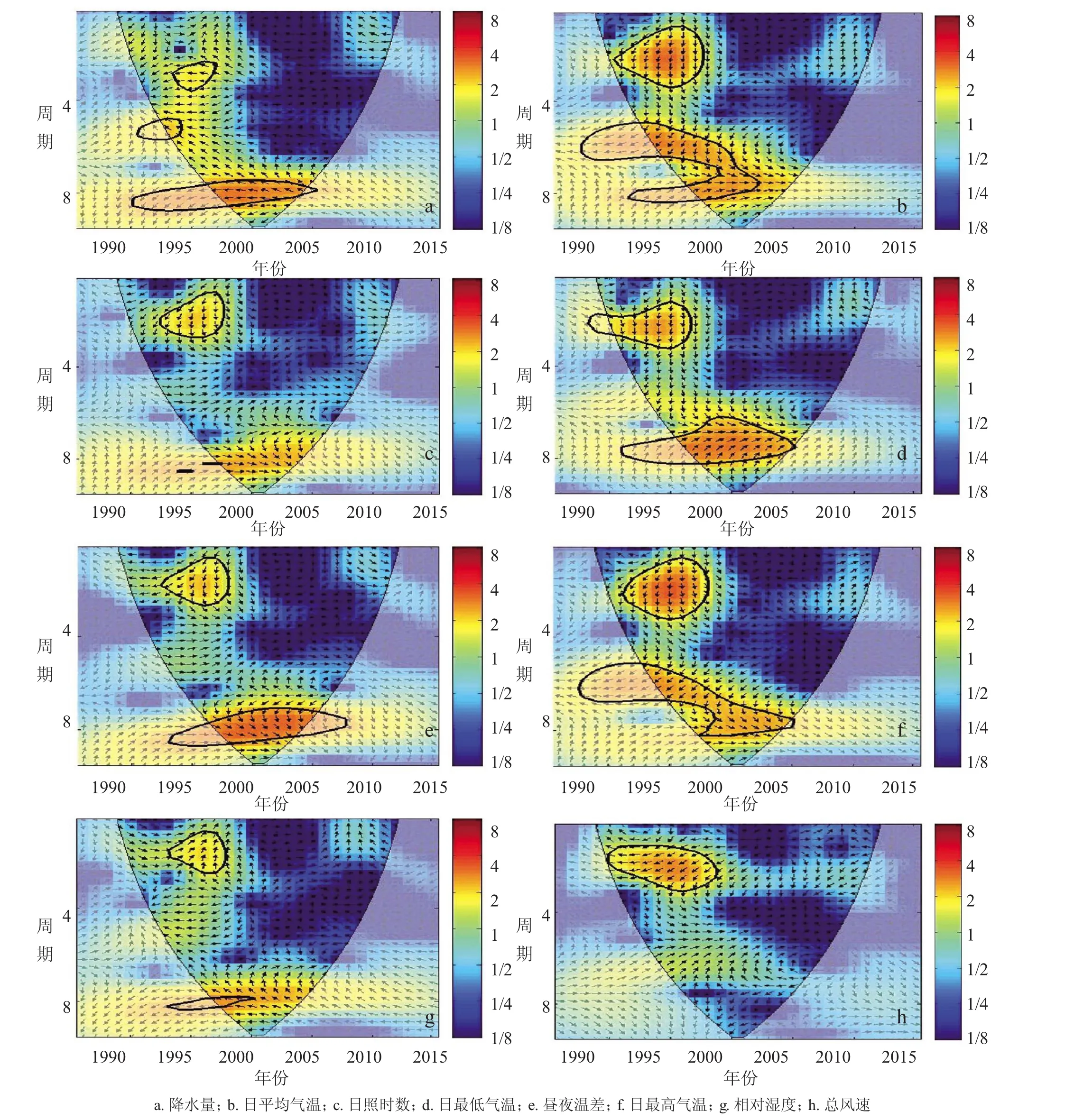
图7 水稻气象产量与孕穗期气象因子交叉小波功率谱

图8 辽宁省1986—2015年水稻气象产量与孕穗期气象因子相干小波谱

在低能量区，气象产量与总风速没有通过95%置信水平的显著周期；气象产量与日最高气温、日平均气温和日最低气温间显著周期基本一致，气象产量变化位落后气象因子90°；气象产量与累计降水量、累计日照时数、昼夜温差和相对湿度显著周期不同，且位相较乱。

3 结论与讨论

经过对多年水稻产量与同期气象因子进行统计分析，得出结论：

1）辽宁省水稻气象产量存在5～8年和2～3年的显著周期，自2001年之后，水稻在频率上的能量强弱分布不显著，表明气象产量连续丰年的周期在变长。

2）对水稻生育期内的总降水量、相对湿度、平均日最低最高气温、平均昼夜温差、平均气温、降水总量、日照总时数和总风速进行了连续小波分析，结果除总降水量外，其他气象因子均存在不同的显著周期。

3）在水稻的分蘖期，气象因子对水稻气象产量的影响主要集中在2～3年的显著周期；降水量与气象产量无明显的相关性。在水稻的孕穗期，气象因子对水稻气象产量的影响主要集中在1～3年的显著周期。风速越小越有利水稻产量增加。

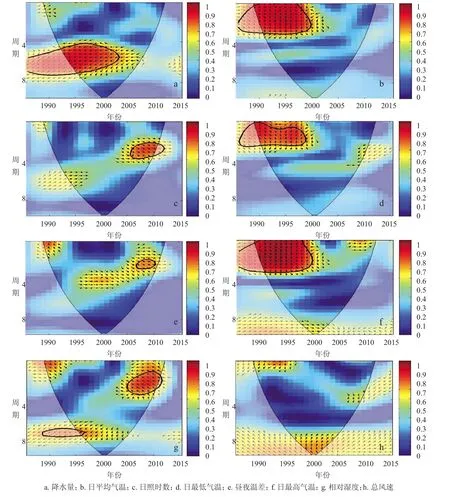
图10 水稻气象产量与开花结实期气象因子相干小波谱

本研究采用小波分析的方法来分析全省水稻的营养生长和生殖生长阶段气象产量与不同气象因子的时序关系，未考虑不同地区不同品种的影响。同时，也未突出特殊极端天气对水稻产量的影响。在今后的研究中，将细化不同地域不同品种间的营养生长和生殖生长的时间点，研究气象灾害对水稻产量的影响变化规律。

参考文献：

[1]陈柏林.气候对常德地区水稻产量的影响 [J].气象学报,1983(4):452-459.

[2]涂悦贤.广东省水稻生产与农业气候的关系[J].热带地理,1989(2):108-116.

[3]许信旺,孙满英,方宇媛,等.安徽省气候变化对水稻生产的影响及应对[J].农业环境科学学报,2011,30(9):1755-1763.

[4]张 宇,王馥棠.气候变暖对我国水稻生产可能影响的数值模拟试验研究[J].应用气象学报,1995(增刊1):19-25.

[5]沈陈华.气象因子对江苏省水稻单产的影响[J].生态学报,2015,35(12):4155-4167.

[6]唐余学,罗孳孳,范 莉,等.基于关键气象因子的中稻单产动态预报[J].中国农业气象,2011,32(增刊1):140-143.

[7]GRINSTED A,MOORE J C,JEVREJEVA S.Application of the cross wavelet transform and wavelet coherence to geophysical time series[J].Nonlinear Processes in Geophysics,2004,11(5/6):561-566.

[8]陈 涛,孙卫国,程炳岩.交叉小波变换在河南降水时频分析中的应用[J].南京气象学院学报,2002,25(5):685-692.

[9]LONNIE H,HUANG J P.Bivariate wavelet analysis of Asia monsoon and ENSO[J].Advances in Atmospheric Sciences,1996,13(3):299-312.

[10]魏中海,王建勇,夏宣炎.粮食产量预测的因子处理和建模方法[J].华中农业大学学报,2004,23(6):680-684.

[11]刘占明,陈子燊,路剑飞,等.广东北江流域降水时空分布及其与Nio3区SST相关性分析 [J].自然资源学报,2013,28(5):786-798.

[12]余丹丹,张 韧,洪 梅,等.基于交叉小波与小波相干的西太平洋副高与东亚夏季风系统的关联性分析 [J].南京气象学院学报,2007(6):755-769.

[13]TORRENCE C,COMPO G P.A practical guide to wavelet analysis[J].Bulletin of the American Meteorological Society,1998,79(1):61-78.

[14]徐科军,李永三.基于连续小波变换的功率谱估计方法[J].应用科学学报,2003,21(2):157-160.