最优环境税、影响因素及配套政策效果研究

金成晓 张东敏 王静敏

一、文献述评

1990年代以来，研究者们开始在经济增长框架下引入环境因素，探索最优环境税的选择及其与经济增长的关系问题。纵观以往文献，主要从两个角度进行研究：一是从污染影响生产效率的角度分析，

纵览以往研究，我们发现以下问题：第一，以往大部分研究把污染或者环境质量纳入到效用函数或生产函数中，实际上，在现实中，并不是所有消费者都认为污染或者环境质量是影响效用的，但是健康水平是直接影响效用水平的，比如健康的人在饮食方面受到的限制就比较少，如消费同样的商品，糖尿病人可能效用为负，而健康的人效用却为正，因此将健康直接引入效用函数更能看出污染通过环境质量进而影响健康，最终影响效用的传导机制。另外污染对生产的影响主要是通过影响劳动者健康水平，进而影响劳动供给或者劳动生产率，最终影响经济增长的，而健康水平并不单一的取决于污染，还取决于健康存量、健康生产投入时间等等，如果直接将污染纳入生产函数会夸大污染的负向作用，进而推出应该征收较高环境税的结论。因此，在效用函数和生产函数中直接引入健康因素，才能够真实地反应污染对效用及生产的影响。第二，将物质资本和人力资本合并统称为资本，认为污染影响总体生产效率水平，实际上，污染对物质资本和人力资本的影响机制是不一样的，污染通过对健康产生影响进而影响人力资本积累，最终影响产出，污染对健康人力资本的影响越大，产出下降得越多，物质资本的积累越慢，由此可见，污染对物质资本的影响是通过对人力资本的影响实现的，因此，探讨污染对人力资本的影响更能反应污染对经济的真实影响。第三，没有考虑资本所得税和劳动所得税对最优环境税的影响，实际上，资本所得税和劳动所得税都是扭曲性税，会影响经济增长，如果降低资本所得税和劳动所得税，一方面市场部门的劳动供给时间增加，有利于产出增加，进而使得污染增加，最优环境税应增加；另一方面，健康生产时间减少，健康水平下降，不利于产出增加，污染可能减少，最优环境税下降。总之，资本所得税和劳动所得税的存在会对最优环境税的选择产生影响。由于我国过去30多年经济的高速增长主要依赖于“人口红利”和“资源红利”，随着我国老龄化社会的到来，人口红利将逐渐消失，长期粗放型经济增长方式亦使得我国即将面临资源枯竭的问题，传统“人口红利”和“资源红利”很难继续作为支撑我国新一轮经济增长的驱动力，因此，只有转变经济增长方式，谋求从“人口红利”和“资源红利”向“科技红利”转变，才是唯一的出路，因此，在创新驱动内生增长理论框架下研究我国经济问题更具有现实指导意义。基于以上考虑，在此拟在一个创新驱动内生增长模型中，引入健康生产函数，在假定污染影响健康进而影响经济增长和福利水平的框架下探讨最优环境税的选择、影响因素及其配套政策的效果，以期对经济可持续增长理论推进和我国税收改革实践贡献一份力量。

二、模型框架

(一)家庭

假定经济是由连续同质且无限寿命的代表性家庭组成，每个家庭只有1个个体，且无人口增长，代表性家庭的效用水平取决于消费和健康水平，而健康水平取决于家庭用于健康生产的时间和污染水平，健康函数采用如下形式：

(1)

其中，ht表示t期健康水平，假定健康是流量的主要原因有两个，第一，我们关注的是污染的直接影响；第二，健康不同于知识，知识可以传递给下一代，但是健康不能。Pt表示t期污染水平，χ表示健康污染弹性，表示污染每增加1%，健康水平下降的百分比，Lht表示家庭t期用于健康生产的时间，包括休闲、参加体育锻炼、看医生等有利于健康改善的活动所消耗的时间，γ表示健康生产弹性，表示健康生产时间每增加1%，健康水平增加的百分比。

(2)

其中，Yt表示t期产出水平，Zt表示t期政府污染治理支出，其中ω表示污染pt关于Yt/Zt的弹性，同时ω也能体现污染治理效率大小，同等条件下，ω越大，表示污染治理效率越低。

(3)

其中，Ct代表t期消费水平，ε代表家庭健康偏好，ε大小反映了健康水平对效用的贡献大小，ρ代表时间贴现因子。为了简化问题分析，假定家庭拥有的时间禀赋是1，家庭预算约束如下：

(4)

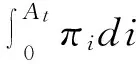
为了求解家庭效用最大化问题，构建现值汉密尔顿函数如下：

(5)

其中，λt表示资本的影子价格，用汉密尔顿函数分别对消费Ct、健康生产时间Lht及资本存量Kt求导，得出如下最优化条件：

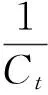
(6)

(7)

(8)

以上条件只是实现最优化的必要条件，实现最优化还有一个充分条件，即横截性条件：

limλtKtexp(-ρt)=0

(9)

(二)最终产品生产部门

假定最终产品生产部门在生产过程中排放一定的污染物，为了遏制企业肆意进行污染排放，政府直接针对污染大小征收环境税τpt，为了简化分析，假定企业每生产1单位产出，产生1单位污染，假定代表性企业的生产函数如下：

(10)

参考Fogel(2002)*Fogel R,“Nutrition Physiological Capital and Economic Growth”, Senior Policy Seminar on Heath,Washington DC,2002.、Zon 和 Muysken (2001)，将健康的改善看做是一种劳动增进型的技术进步，其中，LYtht表示投入到最终产品生产部门的有效劳动量，xt(i)代表t期中间投入商品i的投入量，其中i∈[0,At]，α表示中间投入商品的产出弹性，最终产品生产部门厂商通过选择投入劳动力的数量和中间产品投入量实现利润最大化，最终产品生产部门代表性厂商的利润函数如下：

(11)

其中，ωt表示有效劳动工资，p(i)表示第i种中间产品的价格，由利润最大化条件可以得出：

pt(i)=(1-τpt)(LYtht)1-ααxt(i)α-1

(12)

(13)

(三)中间产品生产部门

中间产品部门通过购买R&D部门生产的专利，同时租借一定的资本生产中间产品，为了简化，假定每生产一单位中间产品需要从市场上租借一单位资本，租借成本为rt，由于中间产品部门生产需要购买一定的专利，因此，中间产品厂商具有一定的垄断性，垄断利润为：

π=p(i)x(i)-rtx(i)

(14)

中间产品部门的利润最大化条件如下：

rt=α2(1-τpt)(LYtht)1-αx(i)α-1

(15)

利润函数为：

πt=α(1-α)(1-τpt)(LYtht)1-αx(i)α

(16)

(四)研发部门

假定知识生产取决于R&D部门有效劳动投入量及经济中的知识存量，知识生产函数如下：

(17)

其中，htLAt表示投入到研发部门的有效劳动数量，At代表知识存量，δ代表研发部门生产效率。假设知识生产部门是完全竞争的，根据无套利条件可以得出：

(18)

R&D部门生产知识的价格等于中间产品生产部门垄断利润的贴现值：

(19)

在这里，ru代表实际利率。

(五)政府

政府除了征收环境税外，还征收资本所得税τk和劳动所得税τL，政府支出主要包括两部分，一部分是污染治理支出Zt，另一部分是用于提供公共服务的支出Gt，假定公共服务支出占总产出的比例是β，政府在每一期保持预算平衡，即政府预算约束满足如下方程：

τkK+τLht(1-Lht)+τptYt=Zt+βYt

(20)

为了实现专款专用，企业对污染征收的税用于污染治理支出，于是下式成立：

Zt=τpYt

(21)

于是可以推出：

τkK+τLht(1-Lht)=βYt

(22)

(六)社会资源约束

(23)

根据家庭时间禀赋约束，家庭在最终产品部门、研发部门工作的时间加上健康生产的时间应等于1，即下式成立：

LYt+LAt+Lht=1

(24)

三、竞争性均衡求解

(一)竞争性均衡定义

1.家庭通过选择消费和健康生产时间实现效用最大化；

2.最终产品部门厂商通过选择劳动投入量和中间产品投入量极大化自身利润；

3.在资本边际回报rt给定的条件下，中间产品部门通过选择生产中间产品的数量实现利润最大化；

4.R&D部门通过选择劳动投入量最大化自身利润；

5.家庭每期预算平衡；

6.政府每期预算平衡；

7.中间产品市场出清；

8.R&D市场出清；

9.劳动力市场均衡；

10.资本市场均衡。

(二)竞争性均衡组成

为了求出均衡增长路径下各主要内生变量的取值，进一步假设，c=C/K，y=Y/K，s=LA/(1-Lh)，s表示研发部门劳动供给比例，根据竞争性均衡定义，可以求出以下均衡条件：

(25)

p=(τρ)-ω

(26)

h=(τρ)ωx(Lh)γ

(27)

c=(1-β-τρ)y-g

(28)

g=α2(1-tk)(1-tp)y-ρ

(29)

(30)

(31)

g=δ(τp)ωχ(Lh)γs(1-Lh)

(32)

(33)

由式(25)可以看出，健康水平是促进经济长期增长的要素之一，同时也可以看出，用于健康生产的时间是阻碍经济增长的因素之一。由(25)-(33)组成了经济的竞争性均衡方程组，通过该均衡方程组可以得出平衡增长路径上变量(g,y,c,τp,Lh,s,h,p)的取值，代入式(3)，即可求出用单位资本消费和健康水平衡量的效用水平。

(三)参数设定

表1 基准经济参数取值

(四)基准模型模拟能力检验

表2 基准模型模拟能力检验结果

四、最优环境税、影响因素及配套政策效果

(一)最优环境税的选择

表3 均衡状态主要内生变量取值

(二)最优环境税的主要影响因素

由图1可以看出，随着家庭健康偏好的增加，最优环境税水平下降。粗略计算，家庭健康偏好每增加1个单位，最优环境税水平将下降0.13个百分点，产生以上的结果的原因在于，随着家庭健康偏好的增加，家庭会将更多的时间投入到健康生产，劳动供给时间减少，虽然健康水平随着健康生产时间的增加而增加，但由于有效劳动供给水平总体是下降的，因此，产出水平下降。由于我们假定每生产单位产出，产生单位污染，因此最优环境税随着产出水平的下降而下降。

由图2可以看出，最优环境税与健康生产弹性的关系接近线性，健康生产弹性每增加1个单位，最优环境税下降0.36个百分点。健康生产弹性体现的是每投入单位健康生产时间，对健康水平的贡献大小。健康生产弹性越高，说明健康生产的效率越高，在其他部门有效劳动生产效率水平不变的条件下，家庭会将更多的时间投入到健康生产，用于生产和研发部门的劳动供给减少。由于有效劳动供给水平下降，于是产出水平下降，因此污染减少，最优环境税下降。

由图3可以看出，最优环境税随着健康污染弹性的增加而下降，粗略计算，健康污染弹性每增加1个单位，最优环境税下降0.24个百分点。健康污染弹性体现的是每产生单位污染对健康影响程度的大小，健康污染弹性越大，在其他条件不变的条件下，健康水平越低，有效劳动水平越低，产出水平越低，进而由生产导致的污染减少，于是最优环境税水平下降。

图4体现了污染治理效率大小对最优环境税的影响，根据式(2)，对应单位污染治理支出，ω越小，由生产导致的实际污染水平越低，ω越高，生产导致的实际污染水平越高，因此，ω大小可以反映污染治理效率大小，ω越小，污染治理效率越高。由图4可以看出，随着污染治理效率的提高，最优环境税增加，而且最优环境税与污染治理效率的关系近似线性，污染治理效率每提高1个单位，最优环境税增加0.31个百分点。主要原因在于，当污染治理效率增加时，同样产出水平对应的实际污染水平降低，于是健康水平增加，有效劳动供给增加，于是产出水平增加，污染随之增加，因此，最优环境税水平增加。

图1 家庭健康偏好对最优环境税的影响 图2 健康生产弹性对最优环境税的影响

图3 健康污染弹性对最优环境税的影响 图4 污染治理效率对最优环境税的影响

(三)最优环境税配套政策的效果模拟

发达国家的环境税实践表明，环境税的开征往往伴随着必要的配套政策，这些配套政策的实施往往能够帮助经济系统有效规避开征环境税对经济增长和社会福利带来的冲击，这也是为什么发达国家关于环境税的改革往往采用以环境税为中心的一揽子政策。基于此，我们拟对开征环境税的相关配套政策对经济产生的影响进行分析。结合最优环境税的主要影响因素，我们将分析改变家庭健康偏好、提高健康生产弹性、降低健康污染弹性和提高污染治理效率等配套政策对经济产生的影响。

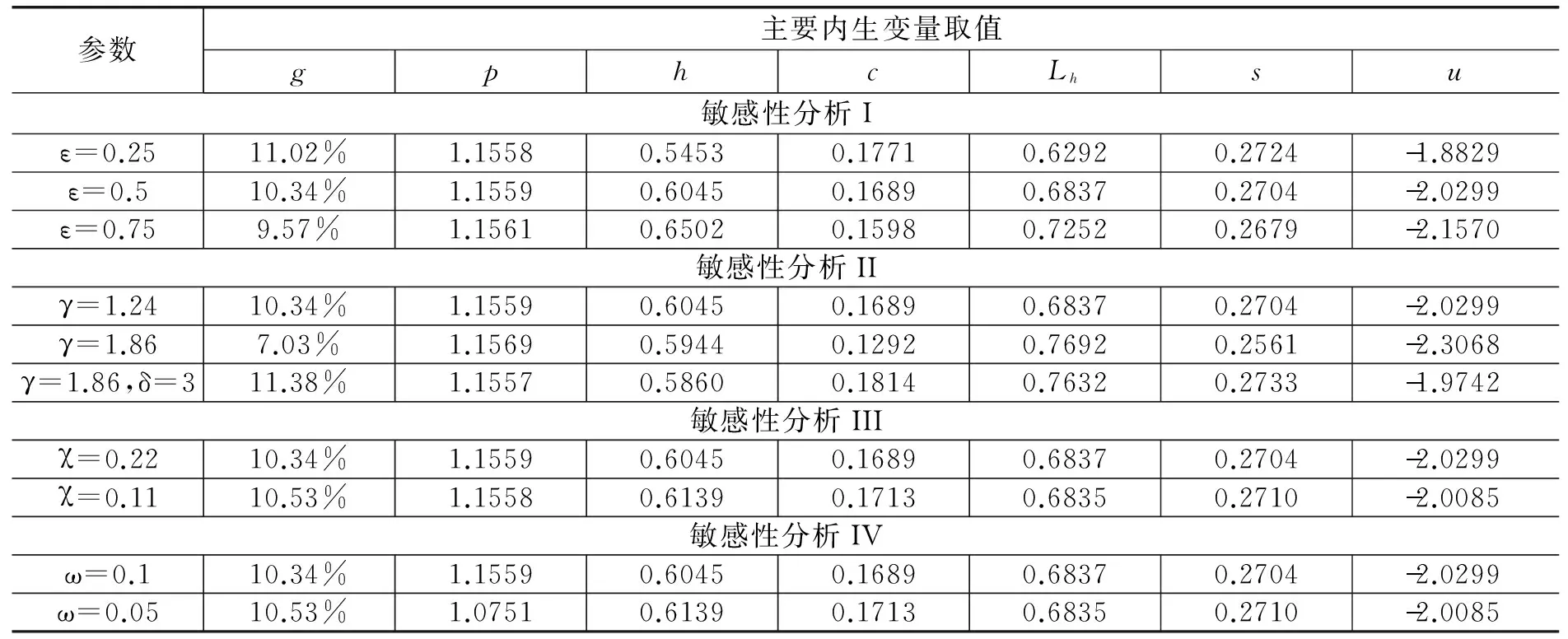
表4 环境税相关配套政策的效果

家庭是生产的主体，为了降低企业污染排放量，可以通过提高家庭健康偏好的方式，敏感性分析I分析了当家庭健康偏好提高50%对主要经济变量的影响。可见，当健康偏好增加50%时，实际污染水平没有下降，反而增加了，主要原因在于，在我们的经济系统中，污染水平与最优环境税大小反向变化。根据前面的分析，当家庭健康偏好增加时，最优环境税下降，实际污染增加，因此，采用提高健康偏好的方式并不能降低污染水平。另外，当健康偏好增加50%时，健康投入时间增加了6.07%，健康水平增加了7.56%，投入到研发部门的劳动时间比例下降了0.92%。由于投入到研发部门的总有效劳动下降了7.45%，而在创新驱动内生增长模型中，有效劳动力投入是经济增长的重要源泉，因此，经济增长率亦下降了7.45%，消费资本比率下降了5.39%。由于家庭效用水平取决于消费资本比和健康水平，在家庭的效用函数中，家庭对健康的偏好程度小于消费，因此，虽然健康水平增加了6.26%，但总体效用水平是下降的。由此可见，采用提高家庭健康偏好的方式虽然能提高健康水平，但是并不能减少污染、促进经济增长及改善福利；当降低健康偏好50%时，我们得到了一个完全相反的结果，污染水平下降了，经济增长率增加了6.58%，福利水平增加了7.24%，但是健康水平下降了9.79%。由此可见，改变家庭健康偏好的方式不能同时实现健康水平改善、经济稳定增长及福利改善，从现实经济中的情况看，家庭健康偏好和健康存量是反向变化的，健康存量水平越高，家庭对健康的关注程度越低，此时家庭会将更多资源投入到生产领域，于是产出水平和福利水平较高。反之，当健康存量水平较低时，家庭对健康的关注程度会提高，此时会将更多资源投入到健康生产，因此，健康水平得到改善，而经济增长和福利水平较低。因此，从可持续发展的角度看，提高健康存量而非健康偏好才是根本出路。

敏感性分析II体现的是健康生产效率提高50%对主要经济变量的影响，可以看出，当健康生产效率提高50%时，用于健康生产的时间增加了12.51%。由前面分析可知，当健康生产效率提高时，最优环境税水平下降，而实际污染水平与环境税反向变化，因此实际污染水平增加，于是健康水平下降了1.67%，用于研发部门的劳动时间比例下降了5.29%，有效劳动力供给水平下降，最终导致经济增长率下降了32.01%，消费资本比下降了23.51%，效用水平下降了13.64%。由此可见，单纯提高健康生产效率的政策既不利于健康的改善，也不利于经济的增长和福利水平的改善，若要通过提高健康生产效率的方式改善健康水平还需要辅以其他的配套政策。主要原因在于，在其他条件不变的条件下，提高健康生产效率意味着其他部门劳动生产率相对下降，致使资源更多的流向健康生产部门，于是产出水平和福利水平下降。因此，为了防止资源过度的集中于健康生产部门，在提高健康生产率的同时，还应采取措施提高其他部门的劳动生产率。在此，我们模拟一下同时提高健康生产部门和研发部门生产效率的政策组合时主要经济变量的变化，假定健康生产效率和研发部门生产效率分别提高50%，计算此时主要经济变量的取值，并将结果总结在表4中，由表4可以看出：当同时提高健康生产效率和研发部门生产效率水平时，与单纯提高健康生产效率比较，健康生产时间增加幅度变小，研发部门劳动投入比例大大增加，甚至超过了健康生产效率未提高的情况，经济增长率增加幅度大大增加，超过基准经济增长率1.04%。由于污染随着产出的增加而增加，健康水平略微下降；由于消费资本比随着产出增加的幅度比较大，效用水平超过了基准经济效用水平。综上，单纯提高健康生产效率水平不利于经济增长和福利改进，需要辅以研发部门生产效率的提高。

敏感性分析III分析了降低健康污染弹性50%时对主要经济变量的影响，健康污染弹性体现的是每增加一单位污染对健康的影响程度。当污染对健康的负向影响降低50%时，用于健康生产的时间减少了0.02个百分点，用于研发部门劳动时间增加了0.22个百分点，由于污染对健康的负向影响下降程度大于健康生产时间减少对健康的负向影响。因此，总体健康水平增加了1.56%，根据式(25)，经济增长率是健康水平的增函数，是健康投入时间的减函数，在降低健康污染弹性50%时，总体经济增长率增加1.84%，消费资本比增加1.42%。在消费水平增加和健康水平增加的共同作用下，福利水平增加1.05%。可见，降低污染对健康的影响既有利于健康水平提高，也有利于经济增长和福利水平改善，同时也说明，在开征环境税的同时，辅以降低健康污染弹性的政策，健康的增长和经济的增长可以同时实现。

敏感性分析IV分析了提高污染治理效率50%时对主要经济变量的影响。可以看出，当污染治理效率提高50%时，对经济的影响和降低健康污染弹性时的影响基本一致，即提高污染治理效率亦有利于健康水平的提高、经济的增长及福利水平的改善，但是二者对实际污染的影响是不一样的。采取降低健康污染弹性50%的政策时对实际污染的影响非常微小，而采取提高污染治理效率50%的政策时使得实际污染水平下降了6.99%。由此可见，若从降低污染的角度考虑，采取提高污染治理效率的方式比降低健康污染弹性更有效。

五、结论与启示

在一个创新驱动内生增长模型中，引入健康生产函数，以中国经济为样本经济，通过参数化和数值模拟的方法分析了在其他扭曲性税收存在的情况下，最优环境税的选择、影响因素及其配套政策效果研究。研究得出，在基准经济下，最优环境税是23.47%，最优环境税随着家庭健康偏好、健康生产弹性和健康污染弹性的增加而降低，随着污染治理效率的增加而增加；提高家庭健康偏好有利于健康水平提高，但不利于经济增长和福利水平改善，降低健康偏好有利于经济增长和福利水平改进，但不利于健康水平提高；单纯提高健康生产效率的政策既不利于健康的改善，也不利于经济的增长和福利水平的改善，同时提高健康生产效率和研发部门生产效率有利于经济增长和福利改进；降低污染对健康的影响既有利于健康水平提高，也有利于经济增长和福利水平改善，但不利于污染的减少；提高污染治理效率既有利于污染减少，又有利于健康改善、经济增长和福利水平改善。本研究一方面为我国开征环境税的税率选择及其配套政策的实施提供了理论指导；另一方面建立了一个分析污染、健康人力资本积累和经济增长关系的基本框架，该框架可以用于比较各种环境规制的政策效果。通过本研究，我们得出以下几点启示：第一，最优环境税税率的制定需要考虑现实经济中家庭健康偏好、健康生产弹性、健康污染弹性及污染治理效率的影响。第二，提高家庭健康存量比提高家庭健康意识更重要，应通过多种途径提高家庭健康存量，如完善带薪休假制度，严格监督食品检疫检验流程，增加公费医疗覆盖面等等。第三，虽然健康水平是经济增长的重要因素，但是研发部门劳动供给效率也是经济增长的重要源泉，如果单纯提高健康生产部门生产效率，将会导致资源过度集中于健康生产部门，进而影响经济增长，因此，若要在提高健康水平的同时不影响经济增长，一方面应加大全民健身设施公共投入，以提高健康生产效率；另一方面，应加大研发部门员工培训投入，以提高研发部门工作效率。第四，应通过加大植树造林投入、建立分类垃圾回收站等方式降低健康污染弹性，减少污染对健康及经济的影响。第五，加大污染技术研发投入，引进第三方治理污染模式，提高污染治理的技术水平和专业化程度，促进污染治疗效率的提高。

在此的研究结论建立在一定的模型假定和基准经济选取上，如果能采用更现实的假定，得到的结论将会更有意义。在以后的研究中，我们将从以下方面进行拓展，在此文中，我们假定健康是流量，事实上，从另外一个角度，健康可以是一个存量，健康水平不只取决于家庭过去对健康生产的投资，还取决于当期的健康生产投资和污染水平，同时随着年龄的增长健康的修复能力下降，类似环境的自我修复能力会会随着环境恶化程度的增加而减弱一样，因此，我们有理由把健康生产当作一个动态的过程，纳入到创新驱动内生增长模型中，相信在这种假定下我们将会得到更有用的结论。