基于优化MUSIC算法的云闪定位技术研究

2018-05-16刘钟中孙秀斌贾岸斌

气象研究与应用 2018年1期

卢舟，刘钟中，孙秀斌，贾岸斌

（1.常德市气象局，湖南常德 415000；2.成都信息工程大学电子工程学院，成都 610225；3.中国气象局大气探测重点实验室，成都 610225）

0 引言

极端天气中的闪电活动是一种灾害性天气现象，以高电压、大电流、强电磁辐射等为主要物理特征，常常造成严重的人员伤亡和经济损失［1］。随着微电子、计算机、电力以及航空航天等技术的不断发展，云闪引起的灾害越来越多，造成的危害也越来越大［2］。云闪过程中辐射的甚高频段信号比地闪辐射的低频段信号所包含的信息丰富很多，可利用云闪对地闪进行预警。因此，研究精度高实时性好的云闪探测系统对云闪放电通道进行定位就显得非常紧要。

由于云闪多发生在云内且具有瞬时性、剧烈性和频繁性，要对其进行准确实时的监测定位仍然有较大难度。近年来，随着计算机技术、电子技术和相关理论的不断发展，云闪定位随之得到快速发展，许多理论方法在实际工程应用中也逐步得到实现。根据张卫杰等［3］所著文章中对数据采集系统的硬件设计可知，用于云闪定位的硬件系统可由云闪VHF信号接收天线、前端信号调理模块、A/D采样模块和FPGA＋DSP数据处理模块等组成。本文采用MUSIC测向算法作为DSP中的解算算法，对其在云闪定位上的应用进行了分析，提出了优化MUSIC算法的方法，并用Matlab仿真了云闪空间谱图。

1 闪电定位方法

闪电是发生于云间、云地间或者云体内的瞬态强放电过程，大致可将其分为云闪和地闪两类。闪电定位主要是通过测量闪电辐射的声、光、电磁场信息，然后计算其相关参数来确定闪电的空间位置，进而推测其活动趋势［4］。云闪定位和地闪定位原理相近，但前者是利用云闪电磁脉冲辐射源发出的甚高频信号，后者则是利用闪电辐射的低频和甚低频电磁波。目前，闪电定位方法主要包括定向法、时差定位法以及时差测向联合法，总体趋于向时差测向联合法（TDOA）发展，该方法是通过多个子站既记录闪电辐射源信号到达时间差又解算其来波信号方向信息来确定闪电空间位置。采用时差测向联合法的多站云闪定位系统空间分布图如图1所示：

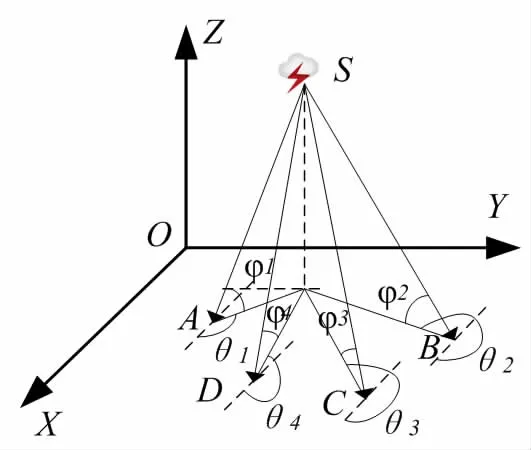
图1 多站云闪定位系统空间分布图

在多站云闪定位系统中，各探测子站的定位误差主要来源于观测时间误差、布站位置误差以及算法误差。本文采用MUSIC算法作为时差测向联合法中的测向算法来测算云闪辐射源信号的方位角和仰角，具有很高的分辨率和实时性，可以提高测向精度、减少定位误差。

2 基于均匀圆阵的二维MUSIC算法

2.1 均匀圆阵模型

均匀圆阵（UCA）是一种具有全向探测能力的阵列，它能同时获取多个云闪辐射源的方位角和俯仰角，从而对云闪进行定位。它由N个相同的全向阵元组成，按等间隔分布在半径为R的圆周上，圆周中心O为球坐标系的原点和云闪入射信号的相位参考点，如图 2 所示［5］［6］。图中，θi和 φi分别为云闪辐射源入射信号的仰角和方位角，i＝1，2，3…。若有P个远场窄带信号源S（t）入射到此均匀圆阵中，则第 i个信源的入射角度为（θi，φi）。

图2 探测系统中的均匀圆阵模型

方向矢量 a（θi，φi）是入射信号（θi，φi）对应的阵列响应，其表达式为［7］：

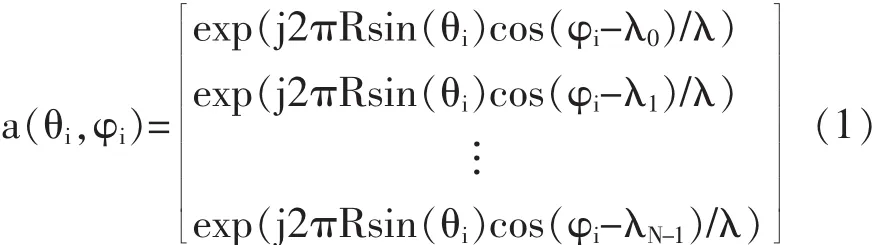
上式中：γm＝2πn/N（n＝0，1，…，N-1）；R 为圆阵半径。

事实上，均匀圆阵所接收到的信号和均匀线阵所接收到的信号是相同的，但是二者对比起来均匀圆阵的阵因子 A＝［a （θ1，φ1） a （θ2，φ2.） … a（θP，φP）］中有入射信号的方位角和仰角两个因子，比线阵的阵因子包含的方位信息多。采用MUSIC算法实现测向对阵列结构没有严格要求，因此可以直接使用均匀圆阵对来波的方位角和仰角进行测量。

2.2 二维MUSIC算法原理

MUSIC算法是通过对均匀圆阵天线所接收到的云闪辐射源信号的协方差矩阵进行特征分解，然后由信号特征值、噪声特征值分别得到信号子空间VS和噪声子空间VN，再利用它们的正交特性对谱函数进行谱峰搜索，最终完成对云闪信号的方位估计［8］。

假设P个窄带信号入射到均匀圆阵天线中，阵元数为M，阵元间夹角为固定值，而且阵元数大于此时的信号数。若这些信号的波达方向分别为（θ1，φ1），（θ2，φ2），...，（θP，φP），阵因子 A＝［a（θ1，φ1），a（θ2，φ2），...，a（θP，φP）］M×P，n（t）为噪声矢量，则阵列输出信号可用下式表示［9］：

相应的输入阵列协方差矩阵为：

其中，RSS＝E［S（t）SH（t）］是信号相关矩阵，σn2是噪声方差。

对2-3式中的RX进行特征值分解得到M个特征值，对应 M 个特征向量 VK（K＝1，2，…，M）。由较大的P个特征值对应信号子空间，较小的M-P个特征值对应噪声子空间。把噪声特征向量作为列构造成噪声子空间VN：

对应于信号分量的导向矢量空间与VN正交，可得到空间谱搜索函数Pmusic（θ）如下式：

通过上式可知，分母中的 VN和 a（θ，φ）正交，所以Pmusic（θ，φ）的值在云闪信源处会有一个很尖的谱峰，此处即为云闪信源的位置。当云闪辐射出多个信号时，可以通过搜索空间谱中的波峰来估计各信号的来波角度信息。二维MUSIC算法处理流程图如图3所示：

图3 MUSIC算法简要流程

3 算法优化

在云闪定位系统中采用MUSIC算法来解算云闪辐射源的方位角和仰角等闪电参数具有很大的优势，该方法具有实时性好、测向精度高、能多信号同时测向等优点。采用MUSIC算法实现云闪定位主要包括空间谱函数构造、信源数估计以及谱峰搜索三个步骤，下面详细介绍对这三个部分的优化。

3.1 空间谱函数优化

对均匀圆阵输出信号的协方差矩阵进行优化处理，充分利用求得的特征值对应的信号子空间和噪声子空间包含的信息。

优化空间谱函数构造方法的实现步骤如下：

（1）采集云闪输入信号样本 X（i），i＝1，2，…N，计算输入协方差矩阵Rx，如公式（2-3）所示，构造新的协方差矩阵RX如式（3-1）：

上式中I为M×M的反向单位矩阵，R^*X为R^X的共轭矩阵。

（2）对3-1式中新构造的协方差矩阵RX进行特征分解重构矩阵得：RX＝UΛH，可得对应的信号子空间RXS1和噪声子空间RXN1如下式：

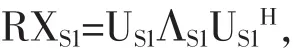
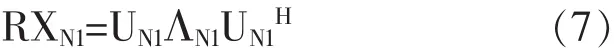
（3）用低秩矩阵代替满秩矩阵RX，再次构造新的协方差矩阵RXX并对其进行特征值分解，重复步骤（2），再一次构造新的信号子空间和噪声子空间［10］：

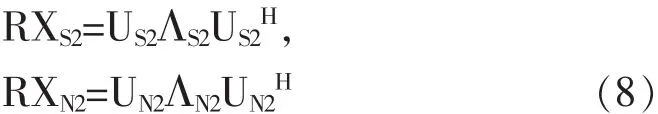
（4）对两次得到的信号子空间和噪声子空间进行平均，如式（9）：

（5）根据US和UN构造新的空间谱函数，如下式：

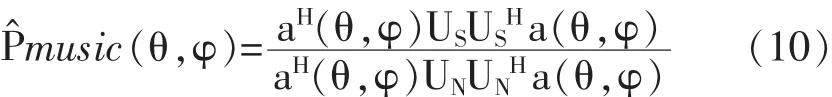
从上式可知，该空间谱函数充分利用了信号子空间和噪声子空间所包含的信息，提高了MUSIC算法的稳定性和在非理想情况下的分辨性能。根据上式进行谱峰搜索，可以得到准确性高、精度好的入射云闪辐射源信号方位角θ和仰角φ。

3.2 信号源数估计优化

在MUSIC算法中估计信号源的来波方向之前需要先估计出信源数，否则会出现虚警或漏警。一般选用基于信息论准则的信源数估计方法来完成该步骤，该方法在有高斯白噪声的情况下能获得较好的估计性能。但是在实际的云闪辐射源探测环境中，天线阵接收到的噪声往往是空间色噪声，这样便不能准确获取阵列协方差矩阵的噪声特征值，从而造成该方法的估计性能较差。为了解决这个问题，采用基于总体最小二乘拟合法来估计云闪信号源数。

基于总体最小二乘法（TLS）的信源数估计方法步骤如下：

（1）算出均匀圆阵接收信号的输出协方差矩阵：

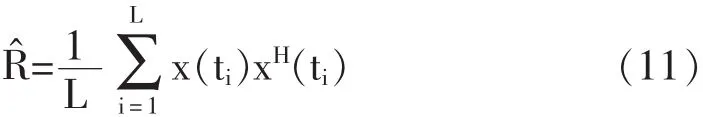
（2）根据MUSIC算法原理可知，对协方差矩阵进行特征值分解可以得到M个特征值，将其按从大到小的顺序排列如下［11］：

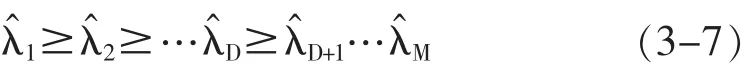
（3）对式3-7中后面的k个特征值进行拟合，拟合点数i（2≤i≤M）从所得特征值个数M到2逐渐减小，依次可以获得对应的拟合偏差 ε（1），ε（2），…，ε（M-1）。

（4）假设云闪入射信号源数为 n（n＝1，2，…，M），因为ε（k）为参与拟合数目的倒数拟合，所以待估计的信号源数目为。按式＝argmin{ε（k）＋p（k）}构造目标估计函数，式中罚函数 p（k）＝1/2k（2M-k）logL，L为快拍数，能够使该式取得最小值的k值就是所要估计的云闪信号源数。

3.3 谱峰搜索优化

由于谱峰搜索在MUSIC算法中耗时较多，影响了云闪定位的实时性，所以在保证一定测向精度的情况下，提出了一种精度高实时性好的搜索方法。（1）采用一个较大的角度搜索步长（如 2°），在［0°，180°］的范围里尽可能寻找出所有极大值出现的大概位置。假设粗略搜索到M个极大值，在没有噪声和干扰信号的情况下，M值等于信源数P。但在实际探测环境中存在无法避免的噪声以及干扰信号，所以会有多于信源数P的极大值出现。此时需要对M和信号源估计数P的大小进行比较，若M＝P则直接进入细搜，否则，将所有峰值依次从大到小排序，选出其中P个最大的极大值，这些值就对应着信号到达方向。（2）在每个经粗选的极大值（i，j）附近采用较小的角度搜索步长（如0.1°）进行搜索，并分别与周围八个点（i-1，j）、（i＋1，j）、（i，j-1）、（i，j＋1）、（i＋1，j＋1）、（i＋1，j-1）/（i-1，j-1）、（i-1，j＋1）比较；如果该极大值大于周围八个点，则其为有效谱峰，（i，j）即为来波信号的方位角和仰角。（3）如果谱峰搜索结果还未达到精度要求，那么返回（2）粗略搜索出的峰值附近继续减小角度搜索步长，重复进行搜索，直到结果满足云闪定位的精度要求［12］。

采用这种一次粗搜全方位多次细搜的优化方法，可以避免在要求较高精度的爬山搜索算法中不必要的计算量，并且可以快速确定云闪信号来波方向的大概角度，然后再通过多次细搜找到满足精度要求的方位角、仰角。优化后的谱峰搜索方法可以极大的减少搜索运算时间，同时提高了云闪定位结果的估计精度。搜索算法流程图如图4所示：

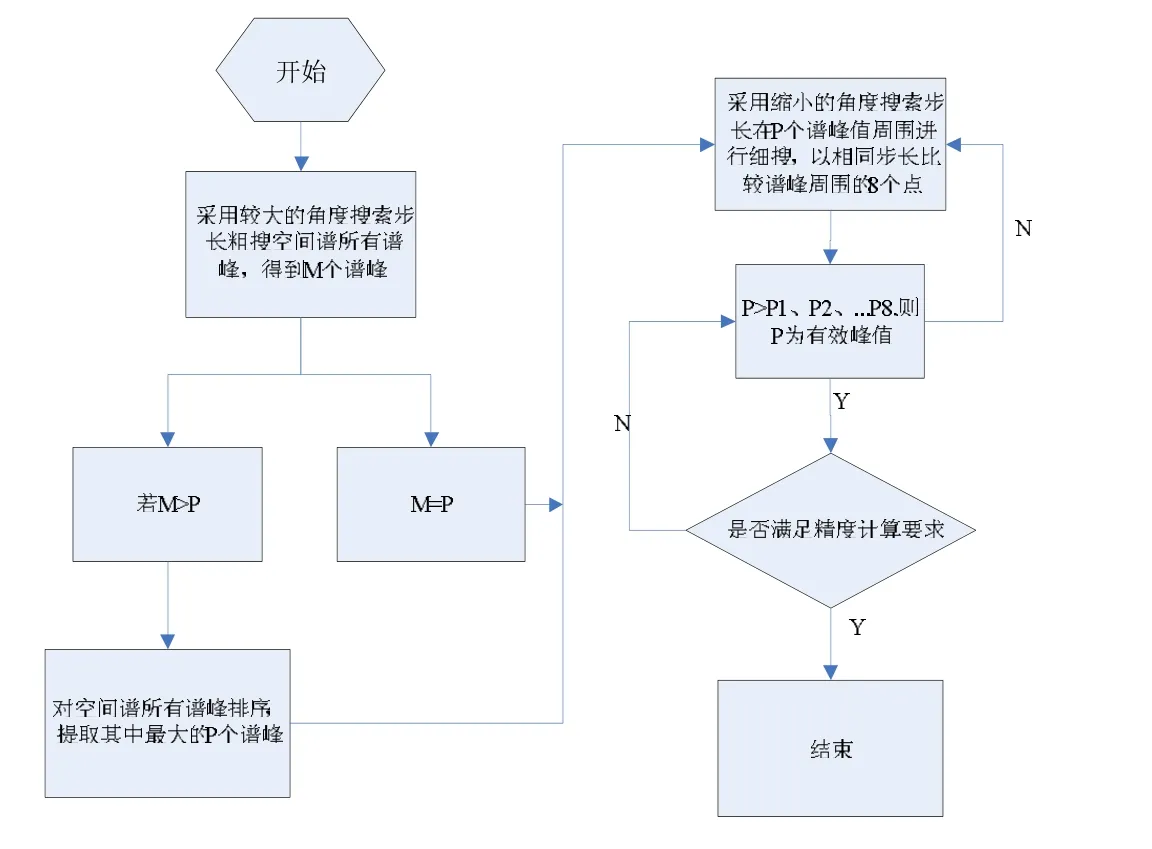
图4 谱峰搜索流程图

4 算法仿真及性能分析

假设均匀圆阵半径满足 r≤1/［4sin（π/M）］，阵元个数 M＝6，快拍数：1024，信号源数 P＝3；信号的方位角分别为（80°、100°、120°），俯仰角分别为（40°、50°、60°），分别在信噪比取 20dB、30dB 的情况下进行二维MUSIC谱估计，如图5（见彩页）、图6（见彩页）所示：

假设均匀圆阵半径满足 r≤1/［4sin（π/M）］，阵元个数 M＝8，快拍数：1024，信号源数 P＝3；信号的方位角分别为（80°、100°、120°），俯仰角分别为（35°、40°、45°），信噪比均为 30dB，二维 MUSIC 算法优化前和优化后的二维MUSIC算法谱估计如图7、图8所示：

通过多次二维分级谱峰搜索获得云闪辐射源的估计方位角、仰角平均值，如表一所示。

表1 两种情况下二维估计仿真结果

通过对比图六和图七的空间谱图可以看出，如果其他条件相同，增大信噪比可以使基于均匀圆阵的二维MUSIC算法DOA估计性能得到提高，对三个信号的分辨能力也得到增强；图7（见彩页）和图8（见彩页）的仿真条件考虑到云闪发生的连续性，针对信源之间的角度间隔可能会比较小进行了设置；将优化前和优化后的二维MUSIC算法进行仿真对比发现，优化后的二维MUSIC算法谱峰更加陡峭，表明对来波方向估计的分辨力得到进一步提升。从表一中的方位角和仰角估计数据可知，优化后的二维MUSIC算法的DOA估计精度得到了很大的提高，并且对多个相隔较近的云闪辐射源信号能够同时测向。

5 结论与展望

本文简要介绍了闪电定位基本方法和均匀圆阵建模模型，重点概述了MUSIC算法中各个重要步骤的优化方法；对算法中构造空间谱函数的方法进行了优化，充分利用了信号和噪声所包含的信息，提高了算法的分辨率；针对实际的空间噪声环境，提出采用基于总体最小二乘拟合法来估计云闪信号源数；针对MUSIC算法中谱峰搜索耗时较多影响定位实时性的问题，提出了一种精度高实时性好的谱峰搜索方法。最后给出了不同信噪比情况下基于二维MUSIC算法的空间谱估计结果，对优化前和优化后的算法性能进行了分析。通过对比分析，可以看到基于均匀圆阵二维优化MUSIC算法作为云闪定位系统测向算法的优越性，使用这种优化的测向方法可以有效提高测向结果的实时性和精度。将这种方法应用于估计云闪辐射源的来波方向，再结合多片并行高速数字信号处理器，可以实时解算多个云闪信号的方位角和仰角，准确获取云闪的空间位置，为云闪定位系统的实现提供了一种更优的方法。

参考文献：

［1］李云敏，孙秀斌，杨崧令，等.云闪定位算法及误差分析［J］.电子测量与仪器学报，2012，26（10）：917-922.

［2］张义军，周秀骥.雷电研究的回顾和进展［J］.应用气象学报，2006，17（6）：829-834.

［3］张卫杰，候孝民.高速大容量数据采集系统设计与实现［J］.电子测量与仪器学报，2005，19（4）：51-55.

［4］张义军，孟青，马明，等.闪电探测技术发展和资料应用［J］.应用气象学报，2006，17（5）：611-620.

［5］ Mathews C P， ZoltowskiM D.Eigenstructure Techniques for 2-D Angle Estimation with Uniform Circular Array［J］.IEEE trans on Sp r，1994，42（9）：2395-2404.

［6］宋士琼，陈旗，胡生亮.基于九元均匀圆阵的MUSIC测向方法研究［J］.计算机仿真，2008，25（3）：123-125.

［7］张小飞，汪飞，陈伟华.阵列信号处理的理论与应用（第2 版）［M］.北京，国防工业出版社，2013.

［8］王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M］.北京：清华大学出版社，2005：82-139.

［9］ SchmidtR.O.Multiple emitterlocation and signal parameterestimation ［J］.IEEE Trans.OnAP， 1986，34（3）：276-280.

［10］赵谦，董民，梁文娟.DOA估计算法的一种修正MUSIC算法的研究［J］.计算机工程与应用，2012，48（10）：102-105.

［11］蓝晓宇.提高空间谱估计分辨率的超分辨测向算法研究［D］.哈尔滨，哈尔滨工程大学，2012.

［12］郭跃，王宏远，陈思捷，等.阵列测向中的精确高速并行谱峰搜索算法［J］. 微电子学与计算机，2007，24（12）：50-54.

［13 潘军，钟一帆，蒙剑.雷电技术在现代建筑中的应用［J］.气象研究与应用，2008，29（3）：49-54.

［14］邹兴奋，刘志辉，李可娟.建筑物防雷接地装置结构探析［J］.气象研究与应用，2010，31（S2）.

［15］黄剑钊.新型国家自动站现场总线CAN的研究及维护方法［J］.气象研究与应用，2016，37（2）：87-89.

［16］张娟，林卓宏，陈巧淑，等.自动气象站观测场防雷接地制式的技术分析［J］.气象研究与应用，2012，33（4）69-71.

［17］姚家钊，陈华宣.基层气象台站防雷问题浅析及解决方法［J］.气象研究与应用，2009，30（1）：78-81.