基于BP神经网络与逐步回归的ERW参数研究

2018-05-16李青龙杜天苍韩宝云

自动化仪表 2018年5期

李青龙,杜天苍,韩宝云

(1.北京化工大学信息科学与技术学院，北京 100029；2.北京石油化工学院信息工程学院，北京 102617；3.中国钢研新冶高科技集团有限公司，北京 100081)

0 引言

焊管厂生产的每一根焊管，从带卷进入生产线到焊管出厂，每个环节经过精细加工，会产生各种参数。每个参数都会由人工或制造执行系统 (manufacturing execution system,MES)记录，以确保焊接质量。精焊作为生产的重要环节，对焊管质量起着重要作用。如果焊接参数稍有偏差，就会使焊管报废。精焊焊接电流过小会引起焊接困难、热量损失，进而导致电弧不稳定，造成未焊透和夹渣等缺陷、熔滴堆积在焊条表面，使焊缝成形不美观。焊接电流过大使得熔深较大，不但容易产生烧穿和咬边等缺陷，而且还会使金属烧损过多，使焊缝过热，造成接头热影响区晶粒粗大，影响焊缝机械性能。因此，控制焊接电流在某一小范围内的稳定值，对焊接质量至关重要。鉴于焊接电流对焊接质量的重要影响，对于工厂技术人员来说，有必要获取便于今后日常生产的有关焊接电流的数据，从而纠正生产过程中产生的异常数据，使得对机器的操纵更具有方向性和指导性，进而提高产品质量和生产效率。为此，本文提出采用逐步回归法建立连接各个物理量之间相互关系的数学模型，用于生产经验和生产数据的预测。同时，考虑到焊接参数的精确度对焊接质量的影响，以及数学模型的局限性，采用改进反向传播(back propagation,BP)神经网络预测数据。

1 逐步回归法

1.1 逐步回归原理

逐步回归法是数学统计模型的方法。其基本思路是将预报因子按其对预报对象的显著程度，逐个引入回归方程；每引入一个预报因子，都要对其进行F检验。当后引入的因子变得不显著时，就将当前引入因子剔除，以确保每引入新的预报因子之前，回归方程中只包含显著性因子。反复进行这样的操作，直到既没有显著因子要引入回归方程，也没有要从回归方程中剔除的不显著因子为止[1]。

1.2 数据来源及分析

本文数据来源于某直缝电阻焊管(electric resistance welding,ERW)厂MES系统。该系统记录并保存大量实时精焊数据。这些数据按每行16个数据的格式被保存在格式为XML的文件中。每列数据对应一个物理量，经C#程序处理读取。在记录的数据文件中，每一行记录值为某一时间点各个物理量的显示状态。不同时间点对应不同状态，但综合来看，一段时间内各个物理量数值均在某一范围内，以确保焊管生产质量。由于同一时间点对应一组物理状态，因此各个物理量之间存在隐函数关系。而对于同一根焊管或者同一批焊管，一天内或者几天内的各个物理焊接参数均稳定在某一范围内。因此，选取某一天数据经程序处理后得出的数学模型，作为未来一段时间内的数据经验模型。

1.3 预报因子及预报对象

本文选取1丝内焊焊接电流为预报对象Y；选取2丝内焊焊接电流、1丝内焊焊弧电压等15个物理量为预报因子[2]，预报对象如表1所示。

表1 预报对象Tab.1 Forecast objects

1.4 数学模型建立

选取MES系统某一天的精焊数据XML文件，经C#程序按原格式提取500组数据。通过统计软件IBM-SPSS22对数据作逐步回归处理，得到数学模型：

Y=-20.57+2.12X3-1.096X4+20.24X5+0.64X1-10.84X13+0.007X6-0.186X7-1.25X2

(1)

2 BP神经网络

BP神经网络是一种单向传播的多层感知器[3-4]，其拓扑结构如图1所示。每个输入节点与隐节点、隐节点与输出节点之间相互连接，每两个连接点之间有权重Wij。

图1 BP神经网络拓扑结构图Fig.1 Topologic structure of BP neural network

2.1 BP神经网络学习过程

BP神经网络学习过程由如下2个过程组成。

①正向传播阶段。

输入信号由输入节点输入，经运算之后经过隐节点，最后由输出节点输出。在正向传播过程中，各个连接点之间的权重Wij为固定值保持不变。由输出节点输出结果得到预测值Y，Y与实际值T之差为误差E。

②反向传播阶段。

输出值与实际值产生的误差信号由输出节点反向传播，经过隐节点后传至输入节点。在反向传播过程中，根据理论计算，逐个修改各个连接点权重Wij。在标准BP反向传播过程中，通过误差信号不断调节各个权重。标准BP算法又称为梯度下降法。

采用BP神经网络对权值进行修改，直到输出值与实际值非常接近为止。

2.2 改进BP算法

在实际应用中，标准BP算法的缺点主要表现为以下三个方面。

其一，学习率η不变导致的学习时间过长，收敛速度慢。在误差信号不断修改权值的同时，学习率保持不变，即误差的改变系数不变，这样在应对复杂情况(如需要多次迭代的网络)或者复杂的大型网络时，误差减小和收敛速度过慢，使网络训练时间变长。

其二，容易陷入误差局部最小解。对于复杂网络，误差函数很可能是一个多维曲面，而在收敛过程中，误差函数可能陷入曲面的某个谷底。而该谷底却不是整个误差曲面的最低点，陷入局部谷底的误差无法跳出，因而无法得到全局最优解[5]。

其三，网络不稳定以及隐节点个数选择困难。

针对标准BP神经网络存在的收敛速度慢和易陷入局部最小值的问题，提出改进的优化算法。

①附加动量法。

标准BP算法在每次对权值Wij进行修改时，没有考虑上一次权值变化对本次变化的影响。权值变化是机械刻板的，因此容易出现局部误差极小点的情况。附加动量法则考虑上一次权值变化对本次权值变化的影响，增加动量项后，其权值变化为：

W(K+1)=W(k)+η[(1-α)D(k)+

αD(k-1)]

(2)

即：

ΔW(k)=η[(1-α)D(k)+αD(k-1)]

(3)

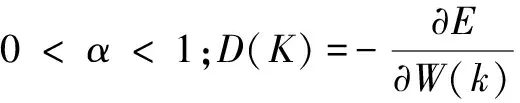
当α=0时，附加动量法则为标准BP梯度下降法；当0<α<1时，后一次权值变化受到了前一次权值变化的影响。当误差曲面处于某个极小点时，附加动量法使权值向着底部平均方向调节。由于0<α<1，因此避免了ΔW(k)=0的情况。

②自适应调整学习率。

标准BP算法收敛速度慢，在很大程度上受到学习率η的影响。当η过小时，网络权值变化速度慢，训练耗时长；当η过大时，权值变化大，从而使得权值有可能超出权值区间，造成网络不稳定，或震荡或发散，无法收敛并达到最优解。为此，采用自适应调整学习率算法。

W(k+1)=W(k)+β(k)D(k)

(4)

(5)

λ=sign[D(k)D(k-1)]

(6)

自适应调整学习率算法，考虑了上一次权值变化梯度方向对本次权值的影响。当上一次梯度变化和本次梯度方向一致时，说明权值变化在向同一方向变化，权值变化慢，此时应该增加学习率，使学习率加快。反之，权值变化正在加快，则应该使学习率减小。自适应学习率使得权值变化智能化，使网络权值变化在稳定的基础上又不失快速性。

本文采用附加动量法和自适应调整学习率相结合的算法。

3 计算试验

3.1 试验过程及结果

为了获取便于今后焊管生产的经验数据，同时纠正生产过程中某一物理量的异常数据，采用MES系统产生的数据作为依据，利用逐步回归法建立了关于1丝内焊焊接电流数学模型。同时，为保证预测准确性和稳定性，采用连续4天内某一时段的150组精焊数据作为预测检验数据。为了使最终结果准确、结论可靠，选择同一天的500组精焊数据作为BP神经网络训练数据，并用接下来连续4天内同一时段的150组数据验证训练后的BP神经网络。最后对逐步回归法和改进BP神经网络的预测结果与实际值之差进行对比研究。误差评价指标[6-8]如表2所示。

表2 误差评价指标Tab.2 Error evaluation indexes

3.2 试验分析

①表2具体列出了误差评价指标的误差最大值、误差最小值、平均误差、误差均方差。从误差最大值和最小值看，BP神经网络误差变化范围明显较逐步回归小；从平均误差看，第四天的逐步回归误差较BP神经网络小；从误差均方差看，BP神经网络较逐步回归预测小，BP神经网络对真实数据的拟合度[9-12]较逐步回归稳定性强。

②从误差最大值、误差最小值来看，为保证焊接质量，焊管焊接过程中焊接参数应保持不变，或者在某一小范围内波动。

3.3 试验结论

3.3.1 试验意义

本文提取了某ERW焊管厂MES系统精焊数据文件。数据分析表明，焊接电流、焊弧电压和焊接速度之间存在数量上的相互关系，并且能够根据这种数量关系，得出焊接过程中各个物理量之间的数学模型。利用这种经验性的模型，便可以提前推测某些物理量在生产过程中的数值范围，这对日常焊接工艺更具方向性和指导性。

3.3.2 试验结果

考虑到焊接参数的数值精度对焊接质量的影响，采用改进的BP神经网络对同一物理量进行预判。结果表明，改进BP神经网络对同一物理量的预测精度要大于逐步回归法，并且BP神经网络法产生的误差波动范围小。因此，如果考虑到焊接参数精确度对焊接质量的影响，应选择BP神经网络进行预测；如果要得出一般性的经验公式，允许有可接受的误差出现，则可以选择逐步回归法。

3.3.3 改进算法效果

改进的BP神经网络较标准BP算法收敛速度快，标准BP算法在迭代次数10 000次内，其均方误差最低降至0.06，训练时间达100 s以上。而改进BP算法的均方误差为0.05，训练时间仅为3 s。由此可见改进BP算法的优越性。