随钻测量仪传感器正交校准方法研究

刘 庆

(中国石油大学胜利学院机械与控制工程学院，山东 东营 257061)

0 引言

从20世纪八十年代中期随钻测量(measurement while drilling，MWD)技术首次在钻定向井中使用至今，MWD得到长足发展并逐步走向成熟[1-3]。随着石油勘探、开采的深入，对MWD仪器的精度也提出了更高的要求。目前，MWD仪器中井底姿态检测系统大多由三向量轴重力加速度计和三向量轴磁通门磁力计(简称磁通门)组成[4-5]。现有绝大部分正交校准算法采用坐标变换矩阵的方法，通过计算理想坐标系与仪器坐标系间的夹角得到变换矩阵，以达到对姿态传感器正交校准的目的[6-7]。但是，该方法在具体应用的过程中，工作量较大、操作繁琐、效率不高。为了改进传统方法的缺陷、简化操作过程、提高工作效率，设计了一种基于随机有限元法的新型高温MWD方案。

1 传感器正交校准模型

1.1 基本假设

基于现有方法存在的局限性，提出了一种便捷、实用的正交校准模型。为了减少操作程序、提高效率，根据大量的试验数据统计结果，在允许的范围内对传感器作如下两点假设。

①传感器输出轴与理想坐标系坐标轴夹角小于1°；

②传感器输出误差可以视作是姿态角度(井斜、方位、工具面)的正弦或余弦函数。

以某重力加速度计为例，证明以上假设的合理性。重力加速度计在井斜角87～93°范围内，输出为1 498～1 500 mV，正弦拟合曲线如图1所示。由图3可以看出，每隔1°进行拟合时，正弦曲线的拟合尚可接受；但超过1°，拟合结果偏差较大，效果不理想。根据现在的生产水平，其加工技术和装配精度满足假设①是较为容易的。

图1 正弦拟合曲线图Fig.1 Sine fitting curves

随钻测量仪器之所以能对井底姿态进行精确测量，是因为随钻测量仪传感器的输出是姿态角度的正弦或余弦函数。

1.2 正交误差消除公式

通过对试验数据的分析，依据上述两点假设的基本原理，在对正交误差进行近似简化以后，可以将重力加速度计和磁通门的正交误差消除公式表示为：

(1)

(2)

式中：Gx、Gy、Gz为重力加速度计的原始输出；Gx′、Gy′、Gz′为经过误差消除的重力加速度计输出；Mx、My、Mz为磁通门的原始输出,Mx′、My′、Mz′为经过误差消除的磁通门输出；xkj(k=1∶6,j=1∶4)为重力加速度计及磁通门的正交误差模型系数；γ为井斜角；Tf为工具面角。γ、Tf可以由传感器原始输出近似求解。

由式(1)、式(2)可知，如能对其中的正交误差模型系数进行解算，就可以得到消除正交误差之后的传感器输出，进而计算出较为精确的仪器姿态信息。

2 正交误差系数解算

2.1 数据采集

基于上述公式，以重力加速度计正交校准为例，按以下步骤对重力加速度计进行数据采集。

①摆置传感器井斜0°、工具面角90°，每转动井斜30°取Gx原始值，直至转过360°，记录每次姿态的井斜值及相对应的Gx原始值。需要指出的是：井斜角变化范围是0～180°，设定Gy值为正时，井斜角为正；Gy值为负时，井斜角为负。

②摆置传感器井斜0°、工具面角0°，每转动井斜30°取Gy原始值，直至转过360°，记录每次姿态的井斜值及相对应的Gy原始值。需要指出的是：井斜角变化范围是0～180°，设定Gx值为正时，井斜角为正；Gx值为负时，井斜角为负。

③摆置传感器方位270°，井斜90°，每转动工具面30°取Gz原始值，直至转过360°，记录重力工具面角及相对应的Gz原始值。

2.2 正交误差系数计算

以2.1节中的步骤①为例，记井斜为ti，Gx原始值为yi，i=1,2,…,n，n=12，则输出与井斜的关系式为:

yi=x11sin(x12ti+x13)+x14

(3)

采用点(ti,yi)拟合式(3)，则需使式(4)最小。

(4)

(5)

3 校准试验

依据上述基本假设，构建数学模型，对某随钻测量仪器传感器进行正交校准。以重力加速度计为例，重力加速度计数据如表1所示。

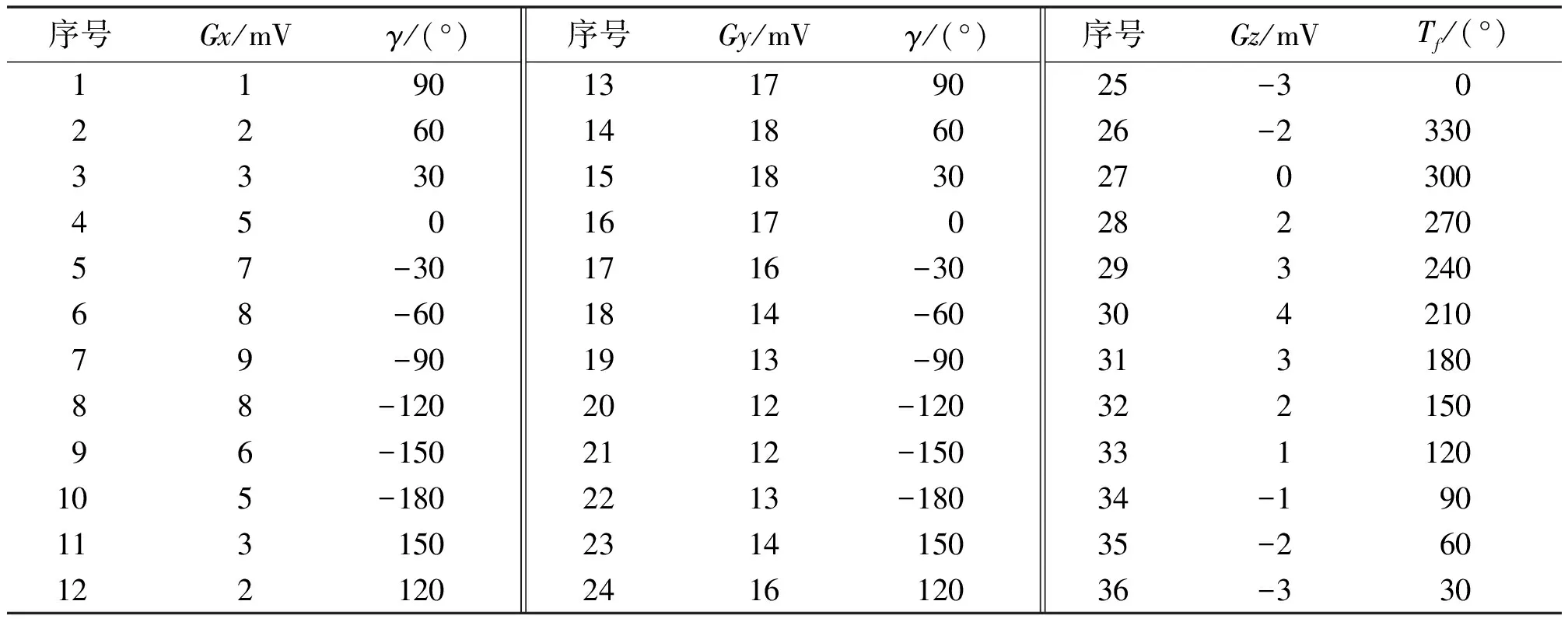
表1 重力加速度计数据Tab.1 Data of gravity accelerometer

重力加速度计正交误差系数如表2所示。校验测试结果如表3所示。

表2 重力加速度计正交误差系数Tab.2 Orthogonal error coefficient of gravity accelerometer

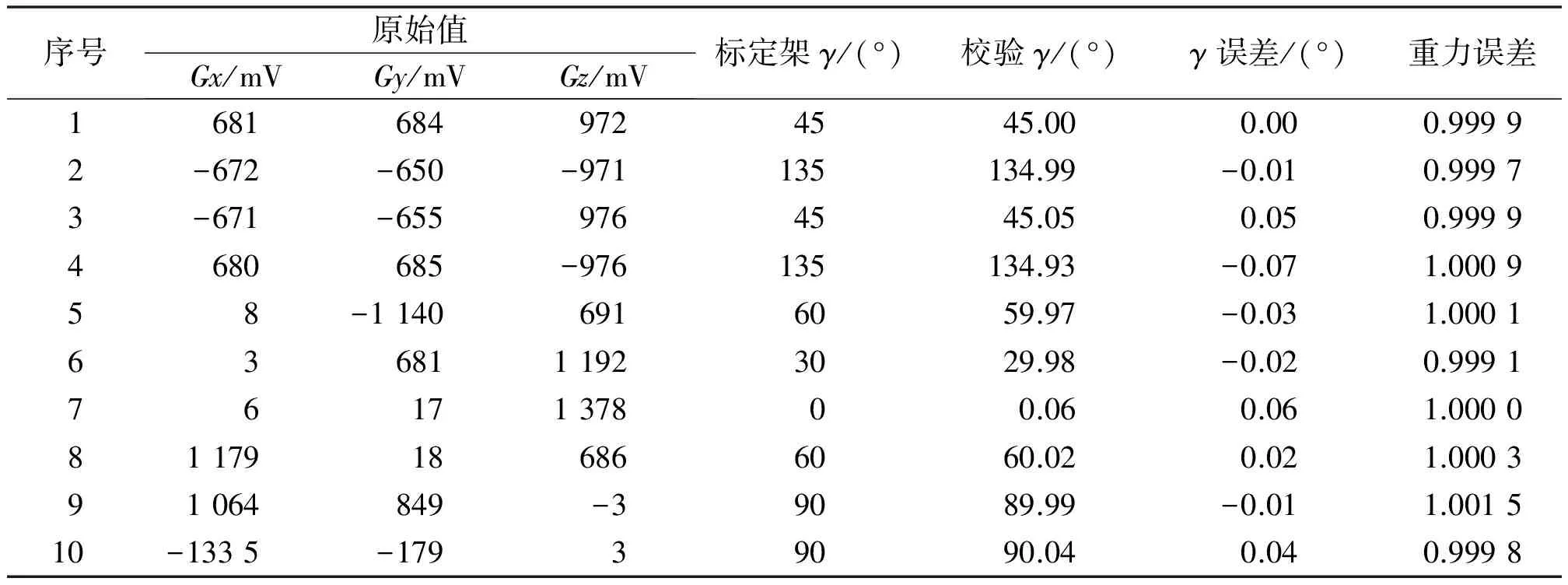
表3 校验测试结果Tab.3 Calibration test results

由表3可以发现，通过一系列的正交校准之后，重力加速度计的正交性得到了很好的保证。通过该方法校准后，随钻测量仪器测斜精度得到大幅度提高。类似地，磁通门也可以进行相同的处理，以提高磁通门测量精度。

4 结束语

针对目前随钻测量仪器传感器标定，提出了一套行之有效的正交校准方法。试验数据的处理结果表明井斜误差均在允许误差范围内。该算法具有一定的通用性，移植简单，可用于随钻测斜及垂直钻井系统；同时，较简单的单多点测斜系统及稍复杂的陀螺测斜系统均适用。目前，该算法已经应用于某随钻测斜项目中，并取得了良好的效果。

参考文献:

[1] 王鹏,窦修荣,艾维平，等.LWD随钻测井系统机械结构设计探讨[J].石油矿场机械,2015,44(2):28-31.

[2] 吕小维,李安宗,张维随，等.钻测量仪测试系统数据采集控制器设计[J].测井技术,2009,33(5):487-489.

[3] 许昊东,黄根炉,张然，等.磁力随钻测量磁干扰校正方法研究[J].石油钻探技术,2014,42(2):102-106.

[4] 叶万聪，胡泽，张淳.随钻地层压力测量装置测量控制系统的设计[J].自动化仪表,2013,34(5):20-22.

[5] 邵佩,刘白雁.垂直钻井工具测斜仪精确校正理论与试验[J].石油学报,2012,33(4):692-696.

[6] 周静,胡毅,付浩.三轴重力加速度传感器标定方法研究[J].石油仪器,2010,24(4):44-46.

[7] 王鑫,史晓锋,林恩怀.油井测斜系统数学建模及校准方法研究[J].测井技术,2009,33(2):103-105.