一种中断驱动系统的时间约束验证方法∗
2018-05-15鞠秀芳
鞠秀芳
(南京大学中国社会科学研究评价中心,江苏南京210093)
0 引言
嵌入式系统是以应用为中心,以解决特定任务为目的,致力于提高应用系统功能、可靠性、成本、体积、功耗的专用计算机系统.嵌入式系统对时间的要求有严格的限制,系统在接到处理请求的同时,必须在规定的时间内响应并完成任务处理.实时性的保证不仅与系统的调度设计有关,还取决于实际运行时系统对事件的具体调度处理和响应时间等.中断是嵌入式系统进行实时响应的重要机制,其触发的不可预测性使得系统运行时的时序较复杂.尤其是在允许中断嵌套的多级中断驱动系统中,一次中断请求在系统响应过程中可能会多次被高优先级的中断挂起,这就给系统的时间约束保证带来了困难.提供有效的中断驱动系统设计和验证方法可以在保证系统功能性需求的同时保证系统的时间约束,并为系统设计的正确性提供保障.
中断驱动系统中,任务的实际执行轨迹是由任务的优先级以及中断源共同驱动的.由于中断触发的不可预测性,且高优先级中断可以随时打断处理低优先级中断的任务,因此,系统可能的运行轨迹组成的空间是无穷的.传统的以测试为基础的方法,无法完全遍历整个运行轨迹空间,其有效性有很大局限性.同时,为使得被测系统按照指定的轨迹运行,需要搭建相应的测试支撑环境,并设计有效的测试用例,测试的代价是相当昂贵的.
当前研究主要是通过自动验证技术,构造系统的行为模型,并运用模型验证技术来验证系统的设计对满足给定的时间约束性的有效性.已有的工作以时间自动机[1−3]和Petri网[4]为建模工具,对应用非抢占式调度策略系统的时间约束进行验证.由于中断驱动系统的任务调度必须是抢占式的,而上述建模工具无法对系统的抢占式调度行为进行建模,因而这些研究工作不能直接处理中断驱动系统.在[5]中,B´erard等研究者提出了中断时间自动机作为描述中断驱动系统的建模工具.中断时间自动机引入一系列局部时钟变量来分别记录各个中断处理任务的执行时间,并通过停表机制来支持高优先级中断的处理任务可以随时打断低优先级中断的处理任务这一抢占式的调度策略.停表机制要求任一时刻,系统中只有唯一的局部时钟变量是活动的,而其它局部时钟变量保持不变.中断时间自动机的主要局限在于它不允许模型中存在全局时钟变量,因此无法满足为中断源建模的需要.以本文中系统为例,这一系统是在外部两个周期性发生的中断源驱动下运行的.在各种嵌入式控制系统中,这种基于多重控制周期性的控制方法,是被广泛使用的控制技术.在对实时控制系统进行验证时,需要同时对中断驱动系统的行为和外部中断源的行为进行建模和处理.显然,中断时间自动机并不能完全满足这样的建模和验证要求.
基于上述分析,本文提出了一种基于线性混成自动机理论,为中断驱动系统及外部中断源进行建模和验证的方法.其基本思想是将线性混成自动机中的变量分为全局时钟变量和中断时钟变量两种:全局时钟变量在任意时刻的变化率都为1,可以用来描述系统运行时刻的外部中断源的行为;而中断时钟变量对应于一个处理任务,只在描述该任务的节点中具有变化率1而在其他所有的节点中变化率均为0.对于一个中断驱动系统,可以定义全局时钟变量来描述系统的上下文、刻画中断源的行为,描述中断触发;而用中断时钟变量来描述响应中断请求任务的行为,进而建立整个系统(中断驱动系统和中断源)的行为模型.
在线性混成自动机表达的行为模型上,系统的时间约束是否得到满足,可以转化为验证系统中是否存在不满足该时间约束的路径,即可以将系统的时间约束验证问题转换为线性混成自动机上的路径可达性判定问题.本文借助模型检验工具BACH[6,7]对该路径的可达性问题进行验证.
1 中断驱动的系统建模
对于中断驱动系统,在某一时刻可能有多个中断请求等待响应.根据中断的优先级,在某一时刻系统响应具有最高优先级的中断,而将其它的请求放入等待队列中.作为应用抢占式调度策略的系统,在中断驱动系统中,高优先级的中断可以挂起正在执行的低优先级中断处理任务而优先得到处理;当高优先级的中断处理结束后,系统会返回继续低优先级中断请求的处理.中断触发的不可预测性使得中断驱动系统的时序较复杂.为了对中断驱动系统进行形式化描述,可以将其行为描述为系统的行为和外部中断源的行为两部分.系统的行为即该中断驱动系统对多级中断请求的调度和响应,外部中断源的行为即中断触发的描述,这往往依赖于系统运行的上下文环境.
线性混成自动机是描述既有连续行为又有动态变化的动态系统的形式化模型,其可达性问题已被证明是不可判定的[8,9].线性混成自动机的定义如下:
定义1线性混成自动机(Linear Hybrid Automata)
线性混成自动机是一个八元组,H=(X,Σ,V,V0,E,α,β,γ),其中:
X={x1···,xn}是一组实数变量,n为H的维数;
Σ是一个有穷的事件集;
V是位置节点的有限集;
v0⊆V是一组初始位置集;
E是一组转换关系,E中的元素具有形式(v,σ,φ,ϕ,v′),其中是一组形如b的转换约束表达式,ϕ是形如x=c的重置变量集,其中,
α是位置集到节点不变式的映射,其中节点不变式是一组形为X)的线性表达式;
β是位置集到变化率集合的映射,其中变化率是形如˙x=[a,b](a,b∈R,x,xi∈X,a≤b)的表达式.对于每个位置节点,每个变量有且仅有一个变化率;
γ是初始位置集v0到初始条件的映射,其中初始条件是形如x=a(x∈X,a∈R)的表达式.
使用线性混成自动机模型对实际系统建模,首先需要抽象时钟变量;然后使用基于时钟变量的表达式描述系统的行为约束.为了直观的描述中断驱动系统,在此我们将线性混成自动机的变量分为全局时钟变量和中断时钟变量两类:全局时钟变量在所有节点的变化率都为1,可以用来描述系统的上下文环境;而每个中断时钟变量都对应一个特定优先级的任务,其变化率只在具有当前优先级的任务节点中为1而在其他节点中都为0.
对于一个中断驱动系统,首先定义全局时钟变量来描述外部中断源的行为,即通过全局时钟变量来控制中断的触发,并根据系统的实际运行建立基于全局时钟变量的表达式,用来刻画中断请求的触发.然后定义中断时钟变量来描述中断驱动系统对中断请求的调度和响应.一般,对于每个优先级的中断请求,均定义一个中断时钟变量来描述系统对该中断请求的响应,所以一个中断时钟变量的取值对应于该中断请求的处理时间,这样就可以建立基于中断时钟变量的系统的时间约束.一般中断驱动系统中还会有非中断任务在执行,对此可以定义具有低优先级的中断时钟变量来描述系统对这些任务的处理.进而根据系统的行为来建立描述整个中断驱动系统的线性混成自动机模型.下面,以一个具体案例来说明.
某周期性中断源驱动的系统在运行前试验时发生故障.通过一系列的故障分析和试验验证,得出结论:发生故障的原因是在通信过程中连续9个周期发生错误,按照预设此时会导致故障的触发.具体的,该系统存在两级和故障相关的中断:高优先级的0.5s控制周期中断和低优先级的4s控制周期中断,在高优先级的中断触发时,系统需挂起当前任务来响应中断.0.5s控制周期中断处理任务分为长周期和短周期,响应时间分别为[155,160]和[193,197].在该系统中,长短周期处理任务中断交替出现;4s控制周期中断是系统的通信请求,需要先后完成发送数据和接收应答参数两部分任务,其中发送数据的响应时间为[345,350],接收应答参数的响应时间为4.6ms(上述响应时间单位均为ms).根据系统的预设行为,若在通信过程中接收应答参数时被中断——即此时高优先级的0.5s控制周期中断触发,则会导致此次通信错误.若在连续9个4s周期中均发生通信错误,则会导致系统故障.
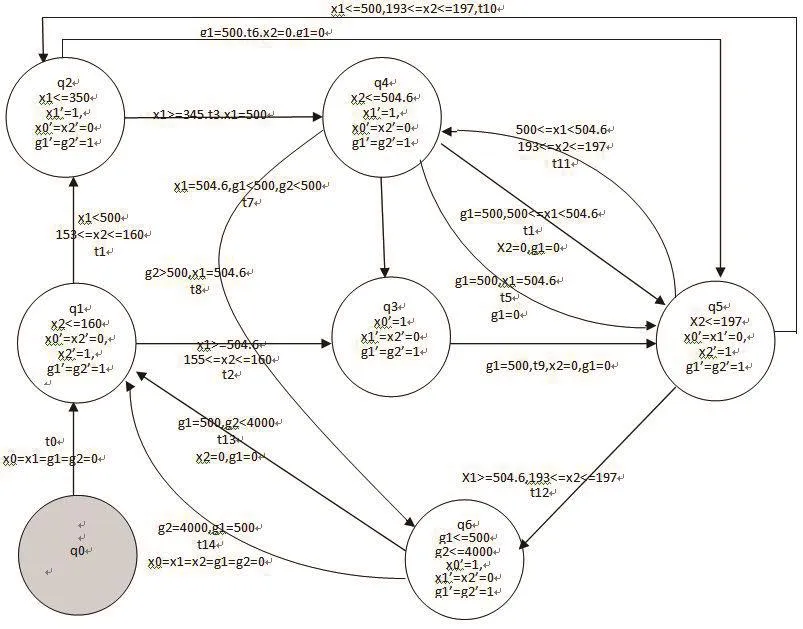
图1 某中断驱动系统的线性混成自动机模型
分析该系统进行建模,首先该中断驱动系统包含两级中断,即0.5s控制周期中断和4s控制周期中断,所以定义两个中断时钟变量x1、x2来分别描述系统对两级中断的响应.同时,定义中断时钟变量x0来描述该系统的空闲行为,空闲任务的优先级最低.接着,定义全局时钟变量来描述中断源.对于周期性触发的中断源,考虑到简化约束表达式,可以针对每个中断源都定义一个全局时钟变量gi.当gi=ci时,其中ci为该级中断的控制周期,则会触发具有该优先级的中断;若该中断请求的优先级较当前正在处理的任务的优先级高,则系统会挂起当前的任务来响应中断.抽象系统的行为,该中断驱动系统的线性混成自动机模型如图1所示.其中,q0为初始状态,q1,q5描述0.5s控制周期中断的短周期和长周期任务处理,对应优先级最高的中断时钟变量为x2;q2,q4分别描述4s控制周期的通信处理任务中发送数据和接收参数,对应的中断时钟变量为x1,其优先级较x2低而比x0高;q3、q6为空闲状态,具有最低优先级的时钟变量x0描述其行为.
根据案例中的描述,系统在通信过程中,若在接收参数时被中断,即发生了高优先级的中断,则会导致此次通信错误.对应于该线性混成自动机模型中,即出发于q4节点的转换是由于高优先级的中断触发(此时g1==500),此时在q4节点的停留时间必然小于4.6ms(对应于500≤x1<504.6),系统发生通信错误.所以若在某次运行时发生转换,则系统发生通信错误.若在连续9个4s控制周期中均触发该转换,则系统发生故障.
2 时间约束的验证方法
前面已提及,线性混成自动机可达性问题是不可判定的,现有的对线性混成自动机完整状态空间一些尝试验证,或者可以解决的问题规模很小,效果颇为有限,或者模型本身有太多的约束.在[10]中,作者针对线性混成自动机的有界可达性验证问题提出了面向路径的有效解决方法,即对线性混成自动机中的一条路径编码得到一组线性约束,进而利用线性规划技术来判断该路径是否可达.
给定线性混成自动机对于形如的位置序列,若对任意的i(0≤i≤n),序列(vi,σi,ϕi,Ψi,vi+1)∈E,则称ρ为H的一条路径.针对路径ρ对每个位置节点添加一个非负实数δi(0≤i≤n),可以得到该路径的一个时间序列
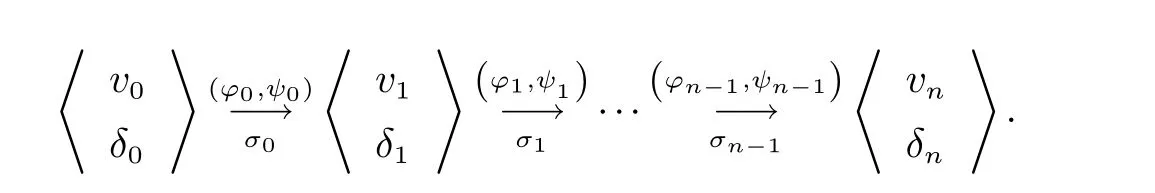
定义2给定线性混成自动机
H=(X,Σ,V,v0,E,α,β,γ)的时间序列若该序列满足下述条件,则该序列表示H的一个行为:
H存在路径:
δ1,δ2,···,δn满足转换约束ϕi(0≤i≤n−1)中的所有变量约束;δ1,δ2,···,δn满足任意位置节点vi(0≤i≤n)的节点不变式.
定义3给定线性混成自动机H中的路径及可达性约束(v,φ),H基于ρ的行为满足R(v,φ),当且仅当v=v该
n行为满足φ的所有变量约束.
基于上述定义,给定线性混成自动机H中的路径及可达性约束R(v,φ),若ρ满足R(v,φ),则必然存在行为满足R(v,φ).那么,δ1,δ2,···,δn必然同时满足ϕi,α(vi)(0≤i≤n)以及φ中的所有变量约束.以上条件构成了关于变量δ1,δ2,···,δn的一组线性不等式θ(ρ,R(v,φ)).若θ(ρ,R(v,φ))有解,那么就存在一组δ1,δ2,···,δn构成满足R(v,φ)的自动机行为.这就是[10]面向路径的可达性验证的基本原理.
基于上述理论,在[6,7]中,作者描述了一个面向线性混成系统有界可达模型检验工具BACH(Boundedre AcheabilityCHecker).BACH集合线性混成自动机图形编辑器、文本编辑器和线性混成自动机可达性验证工具集,提供了针对线性混成自动机的有界可达验证,包括面向路径的可达性验证和有界可达性验证.
对于要验证的时间约束相关性质,首先需要将其在系统模型中描述出来,这可以通过定义满足该性质的节点或是转换来实现,这样就将系统的时间约束判定问题转换为线性混成自动机的可达性问题.进而,根据系统的行为找到描述该性质的路径,借助面向路径的可达性验证技术来判定该路径是否可达,即判定该时间约束性质是否被满足.下面以上一节介绍的周期性中断源驱动的嵌入式系统为例,来说明如何借助BACH的面向路径的可达性验证功能,来验证系统是否会发生故障,即存在某次执行在连续9个4s控制周期中均发生通信错误.
首先需要定义描述该性质的节点或是转换.考虑到该系统是一个周期性中断源驱动的系统,所以可以先建立一个周期上的性质描述,即在一个控制周期中系统发生通信错误.对于该系统,一次4s控制周期中断的处理加0.5s控制周期中断的长周期和短周期任务处理所需要的时间为[698.6ms,711.6ms],即在第三个0.5s控制周期中断触发之前就可以结束4s中断处理任务,因此只需要分析系统的在最开始的1s中的行为.根据前面的分析可得若在某次执行中触发则会发生通信错误.所以,转换关系描述了一个周期中的时间约束性质,即通信错误的发生.
继而需要找到描述该时间约束性质的路径.分析该系统的行为可知,始于q4的转换都是安全的.这主要是因为这些转换都是在第二个0.5s控制周期中断触发或者在等待该次触发时的转换,所以在一个周期的执行中,这四个转换有且只有一个会被触发.至此可以得到在一个周期中系统发生通信错误的路径(根据系统的行为,可以容易的放弃其他路径由于在该系统中,转换关系描述了系统在一个周期后的重置上下文,所以对于性质——连续9个周期均发生通信错误,可以通过重复一个周期里的行为来描述.上述待验证的路径在BACH中可描述为:
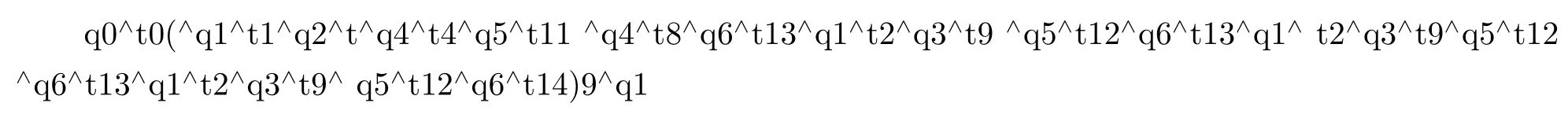
使用BACH online版本BACHOL,在PC(Intel Core2 Quad CPU 2.66G Hz/RAM 4.00G,Java 1.7.0)上对前面得到的模型和路径进行验证.在面向路径的可达性验证功能中,可以在reachability specif i cation选项中添加该待验证路径在最后一个位置节点要满足的规约.在此,针对该中断驱动系统的待验证性质,我们只需要验证上述路径是否可达,没有额外的规约需要满足.添加系统模型,在路径(path)选项中添加待验证的路径,经1.5s左右,可得实验结果如图2:满足可达性约束.即上述路径是可达的.对应该中断驱动系统的描述,其存在发生故障的风险.
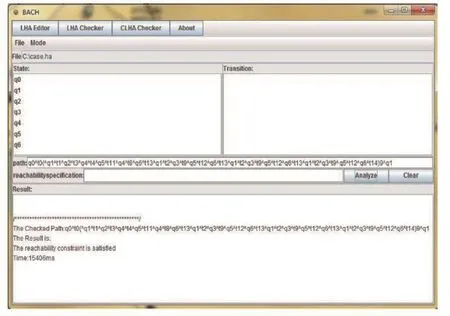
图2 实验结果
3 相关工作比较和讨论
对中断驱动系统的时间约束的保证,传统的以测试为基础的方法无法完全遍历系统的整个运行轨迹空间,其有效性受到很大的限制.同时,测试的代价是相当昂贵的.
随着自动验证技术的应用,通过构造系统的行为模型、借助现有的验证工具来验证系统的时间约束性质成为主要的研究方向.在[1]中,作者应用模型验证理论,对两个调度协议ICPP(Immediate Ceiling Priority Protocol(ICPP))和EDF(Earliest Deadline First)建立时间自动机模型,利用验证工具UPPAAL验证了互斥访问、优先调度等正确性相关性质.但这只是验证协议本身来保证调度协议的正确性,文中的实例验证也只是保证在该调度下系统的功能性需求,而没有给出在该调度下系统满足时间约束相关性质的验证方法.而在[2]中,作者针对满足固定优先级理论假设的实时系统,建立用最坏完成时间(Worst-Case Completion Time)来约束转换的时间自动机模型,利用KRONOS工具来验证任务的响应时间是否满足实际需求、不同任务所需时间的关系以及任务调度间的相关性等性质.在[3]中,作者针对使用非优先级调度的分布实时嵌入式系统提出了一套验证体系DREAM(Distributed Real-time Embedded Analysis Method).DREAM允许使用DML(Domain Modeling Language)直接描述模型,然后利用模型转换将其转换为时间自动机模型,将调度问题转换为时间自动机的可达性问题,进而借助现有的模型检验工具来检验在该调度下任务的完成时间是否满足系统的需求等性质.这些基于时间自动机理论的方法都要求系统的任务调度是不可抢占的,即一个任务必须在一次执行中完成而不允许被新的任务中断;而对于应用抢占式调度策略的中断驱动系统,其一次中断任务的响应可能会多次被高优先级的中断响应挂起,只有在高优先级的中断任务处理结束后方返回继续响应该请求,这无法通过普通时钟变量来描述——普通时钟变量只能描述任务一次执行行为的时间约束,而无法刻画可以被多次打断的可抢占中断驱动系统的时间约束.
此外,还有一些基于Petri网的实时系统调度研究[4].Petri网主要用来描述系统的动态行为,应用时间Petri网可以为一个转换的触发添加时间约束,来描述在转换前的位置的停留时间.基于时间Petri网的实时系统的调度研究,所能描述的系统调度也是不可抢占的,所以仍然无法对应用抢占式调度策略的中断驱动系统进行建模.
在[5]中,作者提出一种新的混成自动机的子类——中断时间自动机(Interrupt Timed Automata,ITA)来描述中断驱动系统.在中断时间自动机中,每个节点都被赋予一个优先级,在每个节点中只有具有当前优先级的时钟变量执行,即其所谓的中断时钟,来描述具有该优先级的中断请求的行为.此外,对转换关系中更新函数的约束使得中断时钟可以准确的描述具有当前中断优先级的中断任务的处理情况.中断时间自动机可以直观的描述应用抢占式调度策略的中断驱动系统的行为,作为线性混成自动机的子类,只允许定义中断时钟变量的约束使得其避免了线性混成自动机可达性问题的不可判定性:中断时间自动机的可达性问题的复杂度为NEXPTIME,在时钟变量数确定时复杂度为PTIME.但只允许定义中断时钟变量而无法定义普通时钟变量的约束,使得在中断时间自动机中无法定义全局时钟;而外部中断源的行为一般是独立于系统行为而依赖于全局时钟的变化,所以中断时间自动机模型对外部中断源的行为的描述有限.对前面案列中描述的中断驱动系统,其周期性中断源的行为就无法通过中断时钟变量来描述:无法通过中断时钟变量来获得系统的全局时钟.显然中断时间自动机并不能完全满足同时对中断驱动系统的行为和外部中断源的行为进行建模和处理的需要.
上述分析表明,针对非抢占式系统的验证工作无法描述中断驱动系统中高优先级中断处理任务可以随时打断低优先级中断处理任务这一基本行为模式.而中断时间自动机由于不支持全局时间变量,无法满足对中断源进行建模的需求.本文提出的基于线性混成自动机对中断驱动系统进行建模的方法,可以很好地满足中断驱动系统的这两个基本验证需求.
4 结论和进一步工作
本文针对中断驱动系统提出了一种基于线性混成自动机有界可达性验证的时间约束验证方法.首先通过抽象中断驱动系统的中断时钟变量来描述中断的响应行为,抽象普通时钟变量来刻画中断的触发,建立中断驱动系统的线性混成自动机模型来描述系统的行为;进而应用线性混成自动机的有界可达性验证和模型检验工具BACH来验证系统的时间约束相关性质.同时以一个周期性中断源驱动的嵌入式系统为例,通过找到与时间约束相关的路径,利用BACH的面向路径可达性验证功能,来验证该性质是否被满足.
目前的研究工作需要设计人员在混成自动机模型上手动标记出待验证的路径.如果模型中存在多条路径对应于待验证的性质,手动标记出所有路径的过程会比较困难且易出错.今后研究工作的重要方面是扩展BACH工具的有界验证功能,使其能够自动找出给定边界内所有的路径,并对这些路径是否满足时间约束进行验证,从而免去用户手动标记路径的工作,提高这一方法的自动化水平和有效性.
参考文献:
[1]Gerdsmeier T,Cardell-Oliver R.Analysis of scheduling behaviour using generic timed automata[J].Electronic Notes in Theoretical Computer Science,2001,42:143-157.
[2]Braberman V A,Felder M.Verif i cation of real-time designs:Combining scheduling theory with automatic formal verif i cation[J].Software Engineering-ESEC/FSE,1999,99:494-510.
[3]Madl G,Abdelwahed S,andSchmidt D.Verifying distributed real-timeproperties of embedded systems via graph transformations and modelchecking[J].Real-Time Systems,2006,33(1-3):77-100.
[4]Cortes L A,Eles P,Peng Z.Modeling and formal verif i cation of embedded systems based on a Petri net representation[J].Journal of Systems Architecture:the EUROMICRO Journal,2003,49(12-15):571-598.
[5]B´erard B,Haddad S,Sassolas M.Interrupt timed automata:verif i cation and expressiveness[J].Formal Methods in System Design,2012,40(1):41-87.
[6]Bu L,Li Y,Wang L,et al.BACH:Bounded reachability checker for linear hybrid automata[C]//In:Cimatti A,Jones R,eds.Proc.of the 8th Int’l Conf.on Formal Methods in Computer Aided Design.IEEE Computer Society Press,2008:65-68.
[7]Bu L,Li Y,Wang L Z,et al.BACH:A Toolset for Bounded Reachability Analysis of Linear Hybrid Systems[J].Journal of Software,2011,22(4):640-658.
[8]Henzinger T.The theory of hybrid automata[C]//In:Proc.of the 11th Annual IEEE Symp.on Logic in Computer Science.IEEE Computer Society Press,1996:278-292.
[9]Henzinger T,Kopke PW,Puri A,et al.What’s decidable about hybrid automata[J].Journal of Computer and System Sciences,1998,57(1):94-124.
[10]Li X,Sumit J,Bu L.Towards an eきcient path-oriented tool for bounded reachabilityanalysis of linear hybrid systems using linear programming[J].Electronic Notes in Theoretical Computer Science,2007,174:57-70.
[11]Bu L,Xie DB.Formal verif i cation of hybrid system[J].Journal of Software,2014,25(2):219-233
[12]Huang Yanhong,He Jifeng,Zhu Huibiao.Semantic theories of programs with nested interrupts[J].Frontiers of Computer Science,2015,9(3):331-345.
[13]Zhu H,Yang F,He J,et al.Linking operational semantics and algebraic semantics for a probabilistic timed shared-variable language[J].The Journal of Logic and Algebraic Programming,2012,81:2-25
