Kagome晶格中的拓扑平带和量子霍尔效应∗

徐雷，张蓓，孔维新，陈楚，张军

(新疆大学物理科学与技术学院，新疆乌鲁木齐830046)

0 引言

量子霍尔效应是二十世纪凝聚态物理中最有意义的发现之一，在过去的三十多年间研究者在此领域做了大量的实验和理论工作．量子霍尔效应首先是在二维电子气中被观测到[1,2]，当均匀磁场应用于二维电子气上，其能带变成Landau能级，此Landau能级具有非平庸的拓扑指标——Chern数[3]．当整数（或者某些分数）个Landau能级被填充时，系统将变为拓扑非平庸的绝缘体，即整数（分数）量子霍尔效应．

自1988起，研究者对无磁场格点模型的整数和分数量子霍尔效应做了大量的研究工作．第一个著名的例子就是Haldane模型[4]．Haldane模型是建立在半满填充的蜂窝状晶格上的，由于模型中引入了净磁场为零的非均匀磁场，整数量子霍尔效应可以稳定存在，而且霍尔电导等于一个拓扑不变的Chern数．最近，由于在时间反演不变的Z2拓扑绝缘体[5,6]研究方面的突破，使得这一领域再次成为研究的前沿．从拓扑学的观点看，Haldane模型和Z2拓扑绝缘体都可以看做广义的整数量子霍尔效应，但是这些体系的单粒子能带都是色散的，它们不支持分数激发，故在这些体系中不能实现分数量子霍尔效应．对于分数量子态，分数Z2拓扑绝缘体在理论上是可行的[7]，但是如何在格点模型上实现这种状态，现在还不是非常清楚，主要困难在于要实现分数量子态则需要强耦合作用．整数量子霍尔效应和Z2拓扑绝缘体基本的拓扑性质都可以通过非相互作用的图像获得，但是对于分数量子霍尔效应，相互作用则是非常重要的．事实上，在上述的格点模型中拓扑非平庸的能带宽度与带隙大小通常是可比较的，甚至是大于带隙的，这就使得体系中很难存在分数拓扑态．这样，即使在分数填充时，由于相互作用弱于关联作用，体系将处于费米液体态而非分数量子霍尔态．因此，在格点上实现类似于分数量子霍尔效应的分数拓扑态的关键在于如何在能带中实现拓扑非平庸的平带．在真实的材料中，严格的平带（带宽为零）是非物理的，因此我们可以放宽限制，只要求带宽远小于带隙宽度即可．

最近，研究者提出了一系列的拓扑平带格点模型[8−19]，有望克服上述困难，从而实现分数量子霍尔效应．这些格点模型都具有类似于Haldane模型和Z2拓扑绝缘体的拓扑非平庸的能带，可以通过调节短程跃迁参数使能带宽度减小至远小于带隙的宽度，进而导致能带接近于平带．特别地，根据抛物线型能带接触机制[8,9]，研究者可以获得一系列的平带模型，它们的带隙与带宽的比值可以达到很大值约20-50．根据接近于平的能带与Landau能级之间的相似性可以猜测[11]：在这些平带模型中，考虑到排斥相互作用，分数量子霍尔效应（或者分数拓扑绝缘体）可以稳定存在．

非常有趣的是最近连续有多个不同的课题组在平带模型研究中取得重要进展[8−19]，他们指出在此模型中可以实现分数量子霍尔效应[11,12]．到目前为止，我们知道在无Landau能级的二维体系中实现分数量子霍尔效应的关键在于能带中存在拓扑非平庸的平带和载流子之间存在相互作用．因此，在无Landau能级的二维晶格中寻找拓扑非平庸的平带结构将显得非常有意义．在本文中我们将详细地研究无相互作用的二维Kagome晶格模型（如图1所示），在无均匀磁场作用下通过简单的调控交错磁通和次近邻跃迁强度来寻找拓扑非平庸的平带结构，从而找到拓扑陈绝缘体．其中a为晶格常数．t1和t2分别表示最近邻（实线）和次近邻（虚线）跃迁强度．每个三角形和六角形内的磁通分别为ϕ和−2ϕ，晶格中总磁通量为零，沿着箭头方向的最近邻跃迁具有相位ϕ/3，次近邻跃迁相位为零．

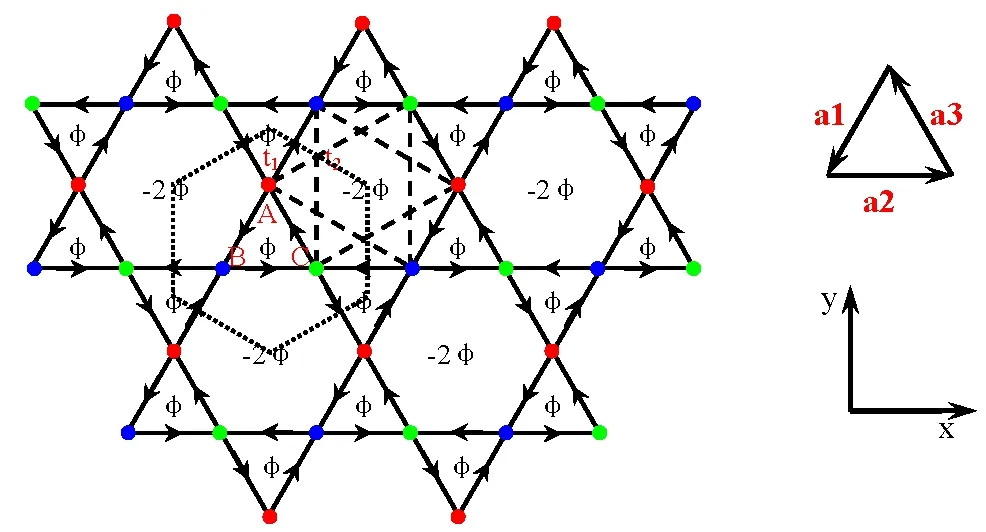
图1 Kagome晶格示意图

点线围成的六边形表示Wigner-Seitz原胞，每个原胞内含有3个原子，分别用A，B，C标记，晶格的基矢为

1 模型和方法

二维Kagome晶格模型如图1所示，其紧束缚模型哈密顿量为

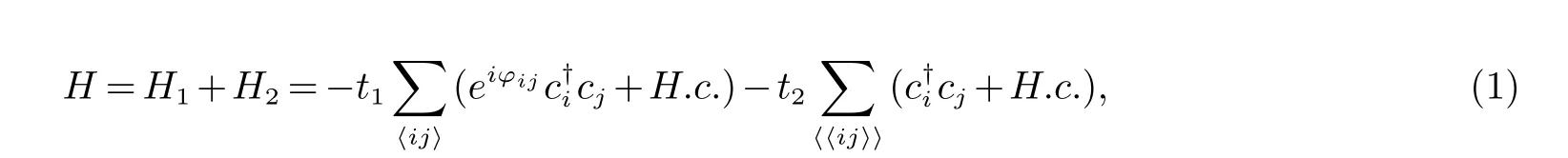
其中表示第i格点上的消灭和产生算符，〈ij〉和〈〈ij〉〉表示最近邻和次近邻格点对，ϕij=±ϕ/3表示加在最近邻格点上的磁通所产生的相位，t1和t2分别表示最近邻和次近邻跃迁强度，H1和H2分别表示最近邻和次近邻跃迁哈密顿量．

将哈密顿量进行傅里叶变换并数值对角化后，系统在零温时的霍尔电导可以通过Kubo公式计算，

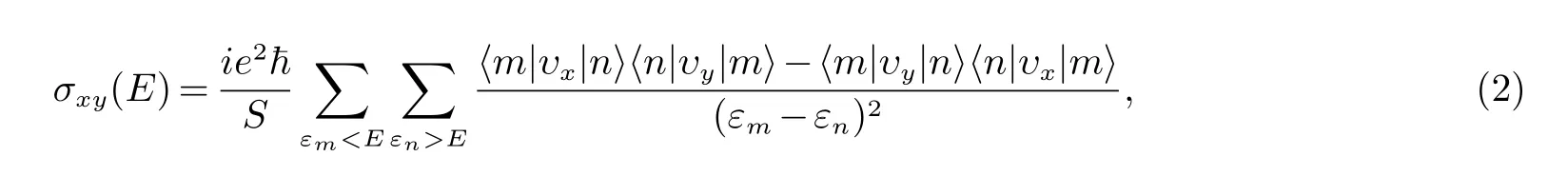
其中S表示系统的面积，E是费米能，εm和εn分别是本征态|m〉和|n〉所对应的本征能量．速度算符定义为是电子的位置算符．当费米能级E位于能隙之间时，霍尔电导可以表示为其中Cm为第m个填充的子能级的陈数[3]．

2 结果与讨论

在周期性边界条件下，经过傅里叶变换系统的哈密顿量在动量空间可以表示为

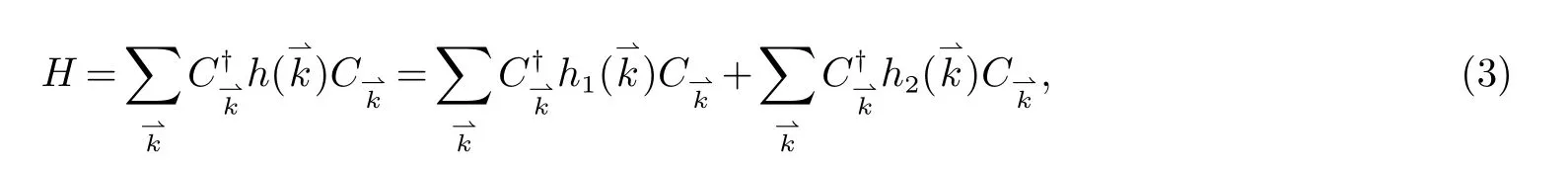
其中分别为最近邻和次近邻跃迁哈密顿量，它们都是3×3的矩阵

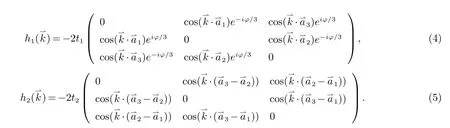
式中分别表示一个原胞内从A到B，B到C，C到A的矢量．

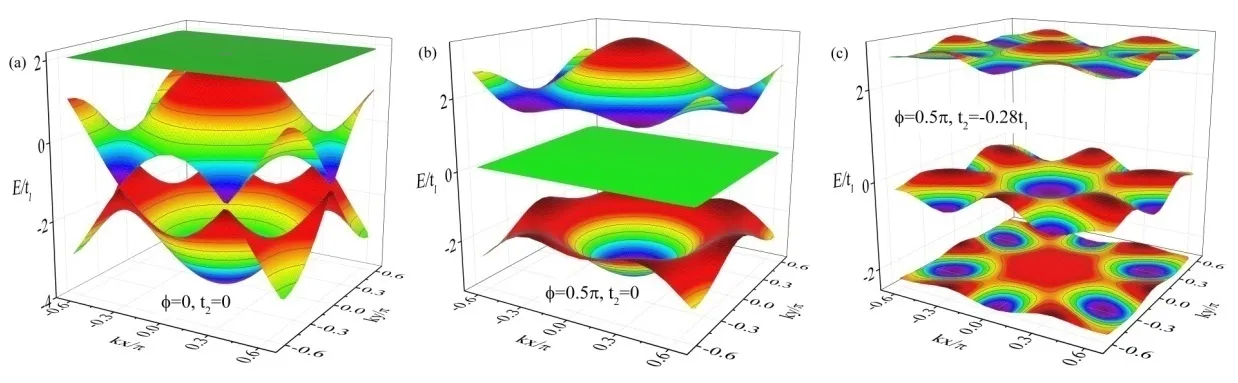
图2 Kagome晶格的能带：（a）ϕ=0，t2=0，（b）ϕ=0.5π，t2=0，（c）ϕ=0.5π，t2=−0.28t1

对动量空间中的哈密顿量（3）进行数值对角化，可以得到不同参数条件下的本征值谱和本征矢量，从而可以计算出各个能带的Chern数．如图2所示，计算结果表明在不同参数条件下，Kagome晶格的能带中都含有三个能带．当交错磁通和次近邻跃迁都为零时（如图2（a）ϕ=0和t2=0），能带的能量值由上到下的关系为Eupper≥Emiddle≥Elower，最高能带的能量值为Eupper=2是个常数．此时三个能带的Chern数均为零，C=0，能带都是拓扑平庸的．只要时间反演对称性不被破坏，这些性质始终存在．如图2（b）所示，当交错磁通ϕ=0.5π时，能带中出现了平带结构，但是此能带的Chern数为零，Cmiddle=0，能带是拓扑平庸的．然而，与此不同的是另外两个能带的Chern数却不为零，Clower=−Cupper=sgn(sinϕ)=1，这表明交错磁通可以改变能带的拓扑性质，能带由原来的拓扑平庸变为拓扑非平庸．

在交错磁通(ϕ/=0和π)作用下，Kagome晶格中部分能级的Chern数为非零值，Clower=−Cupper=sgn(sinϕ)，是拓扑非平庸的能带．因此，在以下计算过程中取交错磁通ϕ=0.5π，通过改变次近邻跃迁强度，来寻找拓扑非平庸的近平带结构．同时，考虑到粒子的激发是从低能级向高能级跃迁，所以期望较低能级具有拓扑平带结构．

如图3（a）所示，给出了带隙与带宽的比值随次近邻跃迁强度的变化曲线．从图中可以很容易发现，当t2=−0.28t1时带隙与带宽的比值最大，Δ12/W≈8，Δ13/W≈23，这里Δ12，Δ13，W分别表示中间能带和最低能带间的带隙，最高能带和最低能带间的带隙，最低能带的带宽．在此条件下，能带结构如图2（c）所示，从图上可以看出最低能带和最高能带的带宽都比较小，接近于平带结构．

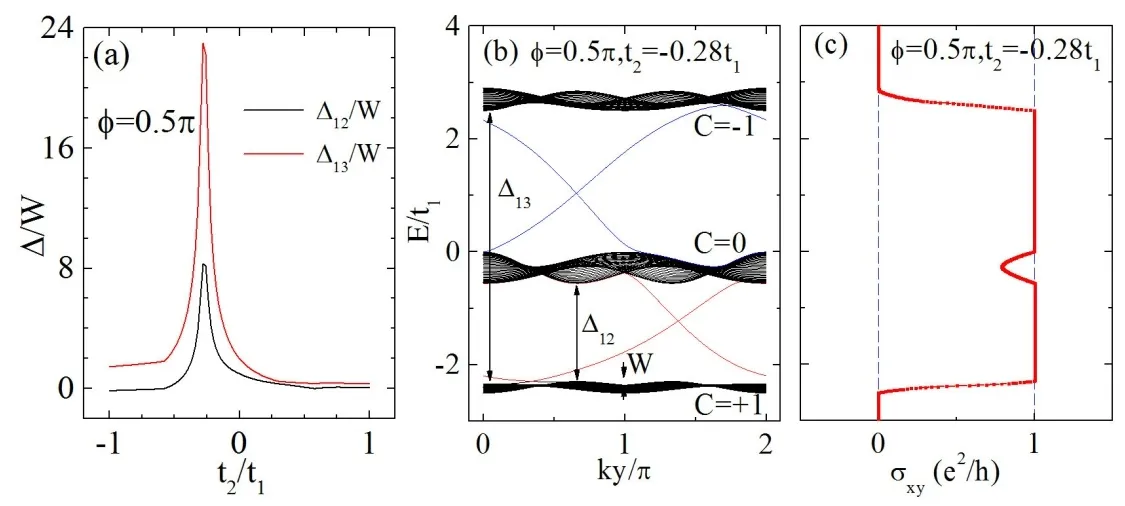
图3 （a）在给定交错磁通情况下，带隙与带宽的比值随次近邻跃迁强度变化曲线；（b）Kagome晶格纳米带的能带结构；（c）霍尔电导

为进一步说明Kagome晶格模型的拓扑性质，我们研究其边界态性质．取x方向为开边界，其宽度为Lx=80a（a为晶格常数），y方向为周期性边界条件，得到一个纳米条带，其对应的能带结构如图3（b）所示．从图中可以看到，最低能级的宽度非常小，而且在两个带隙之间都有一支表面能带随ky增加时，从低能带穿越到高能带，另一支沿相反方向穿越．通过计算发现这两支表面能带分别局域在纳米条带的两个边界，是边界态．如果费米能处于带隙之间，系统将会处于边界态导通的拓扑绝缘态．由数值计算结果可知，图中三个能带的Chern数分别为Clower=−Cupper=1，Cmiddle=0，这正是我们所要寻找的拓扑平带结构．通过Kubo公式（2）计算系统的霍尔电导可以得到，在带隙间具有量子化的霍尔电导值σxy=e2/h（如图3（c）所示），对应量子霍尔态．由于拓扑平带与二维Landau能级的相似性，在系统中加上相互作用将有可能实现无磁场的分数激发，从而产生分数量子霍尔态．

3 结论

本文采用紧束缚模型研究了二维Kagome晶格在交错磁通和次近邻跃迁强度调控下的能带结构．通过改变交错磁通和次近邻跃迁强度，可以找到拓扑非平庸的平带结构，即拓扑陈绝缘体，同时系统中还存在整数量子霍尔态．在此条件下考虑到电子间相互作用有望实现分数量子霍尔态．

参考文献：

[1]Klitzing K V,Dorda G,Popper M.New method for high-accuracy determination of the f i ne-structure constant based on quantized Hall resistance[J].Phys Rev Lett,1980,45:494-497.

[2]Tsui D C,Stormer H L,Gossard A C.Two-Dimensional Magnetotransport in the Extreme Quantum Limit[J].Phys Rev Lett,1982,48:1559-1562.

[3]Thouless D J,Kohmoto M,Nightingale M P,et al.Quantized Hall conductance in a two-dimensional periodic potential[J].Phys Rev Lett,1982,49:405-408.

[4]Haldane F D M.Model for a Quantum Hall Eあect without Landau Levels:Condensed-Matter Realization of the “Parity Anomaly”[J].Phys Rev Lett,1988,61:2015.

[5]Hasan M Z,Kane C L.Colloquium:Topological insulators[J].Rev Mod Phys,2010,82:3045-3067.

[6]Qi X L,Zhang S C.Topological insulators and superconductors[J].Rev Mod Phys,2011,83:1057-1110.

[7]Levin M,Stern A.Fractional topological insulators[J].Phys Rev Lett,2009,103:196803.

[8]Tang E,Mei J W,Wen X G.High-temperature fractional quantum Hall states[J].Phys Rev Lett,2011,106:236802.

[9]Sun K,Gu Z C,Katsura H,et al.Nearly f l atbands with nontrivial topology[J].Phys Rev Lett,2011,106:236803.

[10]Neupert T,Santos L,Chamon C,et al.Fractional quantum Hall states at zero magnetic f i eld[J].Phys Rev Lett,2011,106:236804.

[11]Sheng D N,Gu Z C,Sun K,et al.Fractional quantum Hall eあect in the absence of Landau levels[J].Nat Commun,2011,2:389.

[12]Wang Y F,Gu Z C,Gong C D,et al.Fractional quantum Hall eあect of hard-core bosons in topological f l at bands[J].Phys Rev Lett,2011,107:146803.

[13]Qi X L.Generic wavefunction description of fractional quantum anomalous Hall states and fractional topological insulators[J].Phys Rev Lett,2011,107:126803.

[14]Liu X P,Chen W C,Wang Y F,et al.Topological quantum phase transitions on the kagome and square-octagon lattices[J].J Phys:Condens Matter,2013,25:305602.

[15]He Y C,Sheng D N,Chen Y.Chiral spin liquid in a frustrated anisotropic Kagome Heisenberg model[J].Phys Rev Lett,2014,112:137202.

[16]Simon S H,Harper F,Read N.Fractional Chern insulators in bands with zero Berry curvature[J].Phys Rev B,2015,92:195104.

[17]Zeng T S,Zhu W,Sheng D N.Bosonic integer quantum Hall states in topological bands with Chern number two[J].Phys Rev B,2016,93:195121.

[18]Liang L,Vanhala T I,Peotta S,et al.Band geometry,Berry curvature,and superf l uid weight[J].Phys Rev B,2017,95:024515.

[19]Du L,Zhou X T,Fiete G A.Quadratic band touching points and f l at bands in two-dimensional topological Floquet systems[J].Phys Rev B,2017,95:035136.

[20]Ohgushi K,Murakami S,Nagaosa N.Spin anisotropy and quantum Hall eあect in thekagomelattice:Chiral spin statebased on a ferromagnet[J].Phys Rev B,2000,62:R6065-R6068.