一种改进的投影装置标定方法*

孙秀清,张笃周,王 立,吴奋陟

0 引 言

在轨操控[1-2]和服务的发展对空间航天器局部模块的快速3D模型重建和精密测量技术的需求日益迫切.自旋运动是失效卫星的一般存在状态，转动角速度很快，常规激光成像雷达由于扫描频率较低不适合高速动态目标；FLash Lidar存在探测器面阵小分辨率低且器件难以获得的问题；编码结构光具有自动化程度高、速度快、精度高等特点，是空间非合作目标的三维测量的重要技术方向.

结构光三维测量的过程中，投影装置标定是影响结构光三维测量精度的关键环节.和相机标定类似，投影装置也包括内参数标定，以及投影装置坐标系和世界坐标系之间转换矩阵(外参数)的标定.文献[3]提出了一种基于相移法的投影装置标定方法，标定过程中，将两组不同方向的光栅图像投影到一块带有圆形标志点的平面标定板上；文献[4]提出了一种基于平面的投影装置标定方法，向已知表达式的标定平面上投影棋盘格图像，根据线面交叉点确定投影图像的标定角点的三维坐标.文献[5]提出了一种不需要对相机预先标定的方法，向棋盘格标定板上投影格雷码条纹，首先通过试验得到最优匹配区域，然后在最优匹配区域内计算角点的局部单应性矩阵，通过单应性矩阵直接得到棋盘格角点对应投影装置像平面的位置坐标.以上方法都需要特殊的标定平板，只能在结构光三维测量系统工作之前提前进行标定，在测量过程中，如果三维结构光测量系统参数发生变化，系统无法进行自我修正.

本文采用的编码结构光三维测量系统，由双相机和单投影装置组成，三维重建方式灵活，可以结合立体视觉和编码结构光三维测量两种机制.编码结构光系统可以在测量的过程中，不断修正系统的标定参数，提高测量精度且不需要特定靶标.

1 投影装置模型

投影装置的光线方向和相机的光线方向相反，把投影装置看作一个逆向的相机，可以采用和相机相似的物理模型来描述：

sm=A[Rt]M

(1)

其中，m=[uv1]T为像素坐标系的扩展坐标，M=[XYZ1]T为世界坐标系的扩展坐标，s为比例系数，A为投影装置内参数矩阵，[Rt]为投影装置外参数矩阵，R为旋转向量，t为平移向量.

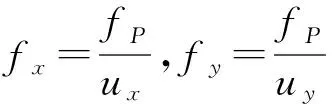
设(x，y)为图像坐标系坐标，(xn，yn)为归一化的物理坐标

(2)

(3)

2 标定方法

2.1 投影装置标定原理

投影装置参数标定的过程中可以采用和相机一致的数学模型，但是却没有办法直接像相机一样，得到像平面标定角点对应物方点的三维坐标，因此，投影装置标定的关键在于如何获得投影图像标定点的空间坐标.采用以下解决方案：

1)投影装置投射水平方向和竖直方向的格雷码条纹，双相机确定条纹三维位置，解码得出条纹在投影装置像平面的位置.

进行投影装置的标定，首先利用结构光双目三维系统中投影装置可以投影编码图案的优势，构造三维标定角点.在实际应用中，可以选择复杂空间编码图案，一次投影就可以依赖双目相机重建出标定角点的三维坐标，为了简化问题，本文选择格雷码条纹进行投影，如图1所示.

图1 四副竖向格雷码编码图案Fig.1 Four pairs of vetical gray code encoding patterns

考虑到投影装置标定的解算步骤和相机标定一致，相机标定时，每幅图像对应的标定点大约为200个，投影装置标定时也需要构造相同数量的空间标志点，投影装置投射6幅格雷码结构光编码图像，投射的次序是1幅全白的图像、1幅全黑的图像、4幅竖向格雷码编码图像，分别投影到标定场景中，并同时用相机捕获.

提取四幅格雷码图像条纹边缘的亚像素级坐标，根据解码得出的投影装置图像单元位置为约束进行匹配，根据三角形准则重建出标定点的3D坐标.双目结构光三维测量系统的示意图如图2所示.

在实际的应用中，由于成像系统噪声和相机标定参数误差等的影响，两条直线可能并不能交于一点，如图3所示，这时用两条直线中垂线的中点代替重建的3D点.

图2 双目结构光三维测量系统的示意图Fig.2 The abridged general view of binocular structured light 3D measurement system

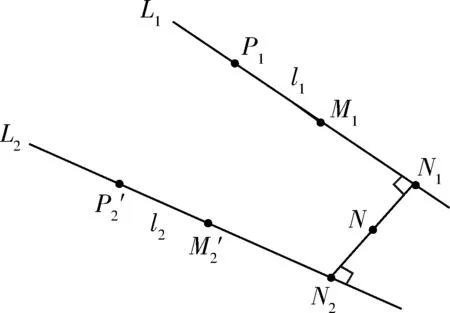
图3 异面直线公垂线中点示意图Fig.3 The abridged general view of crossover line

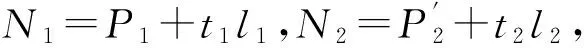
(4)

即

(5)

求解该方程可以得到：

(6)

2)常规投影装置标定，标志点都在一个三维平面上，可以直接采用张正友方法解算投影装置参数.本文标志点根据标定场景的不同而改变，不在一个平面上，相当于利用立体靶标进行标定.

式(1)中设投影装置外参数为[Rt]=[r1r2r3t]，设世界坐标系坐标M和像素坐标系坐标m之间的单应性矩阵为H，则有：

sm=HM

(7)

其中H=λA[r1r2r3t]，λ为任意系数.

H中的元素为

(8)

首先，根据极大似然估计准则，求取单应性矩阵H.理想情况下，世界坐标系坐标M和像素坐标系坐标m符合式(1)，但是由于提取的图像点含有噪声，M和m并不符合式(1)，假设图像点坐标的噪声为高斯噪声，均值为0，协方差矩阵为Λmi，则H的极大似然估计值通过最小化以下函数得到

(9)

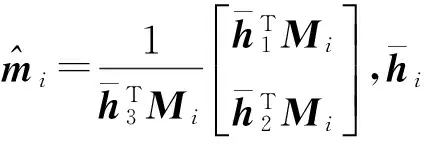
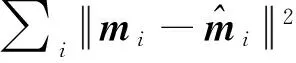
假设h34=1，式(7)可以写为

(10)

当给定n个三维点坐标时，有n个上面的等式，可以写成一个矩阵等式Lx=0，L是一个2n×n个的矩阵，n≥6时，可以得到x的最小二乘解.

假设H=[h1h2h3h4]，从式(7)得到

[h1h2h3h4]=λA[r1r2r3t]

(11)

利用旋转矩阵的正交性，可以得到

(12)

(13)

令

(14)

B是一个对称矩阵，定义一个六维变量

b=[B11B12B22B13B23B33]T

(15)

令hi=[hi1hi2hi3]T，则有

(16)

其中

Vij=[hi1hj1hi1hj2+hi2hj1hi2hj2hi3hj1+hi1hj3hi3hj2+hi2hj3hi3hj3]T

根据式(12)～(13)可得

(17)

假设拍摄了n幅场景，则V是6n×6的矩阵.如果n≥1，可以得到b的最小二乘解.一旦得到b的值，可以计算出所有投影装置的内参数矩阵A，根据式(3)，可以得到投影装置与世界坐标系之间的外参数矩阵.

为了更符合投影装置的实际物理模型，还需要考虑投影装置的畸变系数.畸变系数的求解和张正友方法完全相同，这里不做赘述.

通过最小化下列函数来优化上述投影装置参数，包括投影装置内参数，外参数和畸变系数：

(18)

2.2 投影装置精度验证

投影装置精度验证，需要对对投影装置根据其投影模型恢复投影光线.该方法根据投影装置内参数及相对于基准镜的外参数，按照投影装置模型，由已知物方点坐标计算其在投影像平面的理论坐标，并与实际图像上的位置作差比较，从而计算投影装置标定的像素精度.

图4 投影装置精度验证解算步骤Fig.4 The procedure of accuracy verification

像素精度可以用来衡量投影标定的优劣程度，来判定是否可以满足三维重建的精度要求.

3 标定实验及结果分析

为验证本文方法的实际效果，搭建了一套双目结构光三维重建系统.该系统采用Point Gray公司的相机，分辨率是2 048×2 448，像素尺寸为3.45×3.45 mm，镜头焦距是8.5 mm；闻亭公司生产的投影装置，分辨率是1 140×912，基线距离为400 mm左右，投影装置距基线的前后距离为140 mm左右.

实验时，安置好编码结构光系统后，投影仪投射格雷码图案到标定场景中去，相机同时拍摄含有格雷码图案的标定场景.接着，改变标定场景，重复以上过程，采集若干组标定场景的图片.

图5 两个摄像机拍摄的图片Fig.5 Pictures taken by two cameras

由标定原理可以看出采用该方法单个场景即可以解算出投影装置参数，但是通过多组实验验证，单个场景解算误差较大，不能满足三维重构的精度要求，下面通过实验验证标定场景数量对标定精度的影响，结果如表1所示.

由表1可知：随着标定场景数量的增加，标定参数反算的平均误差逐渐减小，但是由于标定时间和计算量的限制，在实际应用中，标定场景的数量不宜过多，可以根据实际精度要求决定标定场景的数量.

使用标定平面，对此投影装置进行标定，由标定原理可知，在标定过程中，至少需要三组标定图像，通过实验发现，采用七组标定图像，标定误差为△x=0.29 μm，△y=0.18 μm，与本文提出的这种方法精度相当.

利用此三维结构光系统对标准件进行测量，利用一个相机和投影装置重建，测得深度信息误差为

0.058 3 mm，能够满足结构光测量系统的三维重建精度要求.

图6 标定平面进行投影装置标定Fig.6 The calibration of projecting apparatus by using board calibration plane

场景数量fptanαu0v0k1k2平均误差/mm31640.95.33×10-4421.97613.770.00150.67270.00480.012441696.61.17×10-4418.81574.120.0250.36400.00140.001051704.51.17×10-4417.42572.980.0230.36220.00157.0×10-461715.51.28×10-4419.41572.070.0280.22335.8×10-44.8×10-471719.41.78e-05420.17573.410.0300.17652.2×10-41.3×10-4

4 结 论

理论分析和试验验证了提出的改进的投影装置标定方法具有以下特性：1)不需要标定平面或者靶标；2)在实际三维测量过程中，进行投影装置参数的标定；3)在实验室中投影装置标定完成后进行投影装置参数的更新修正.

实际的标定实验验证了这种方法可完成投影装置参数的标定，可随时修正投影装置参数并保持标定精度满足测量要求，且随着标定场景数量的增加，标定误差逐渐减小.

另外，分析表明可使用复杂编码图案进行投影，单次投影即可完成对一个场景的标定，提高摄影机标定的效率.

参 考 文 献

[1] COX G. On-orbit satellite servicing study[R]. NASA Internal Project report, 2010.10:411-416.

[2] MARTIN D H, ANDERSON P R, BARTAMIAN L. Communication satellites[D]. AIAA Aerospace Press Series, 5th edition, Reston, VA., 2007:227-230.

[3] 李中伟，史玉升，钟凯，等. 结构光测量技术中的投影仪标定算法[J]. 光学学报，2009，29(11):15-21.

LI Z W，SHI Y S， ZHONG K， et al.Projector calibration algorithm for the structured light measurement technique[J].Acta Optica Sinica，2009，29(11):15-21.

[4] 符红. 结构光投影三维轮廓测量系统的标定[D].杭州：浙江大学，2013.

FU H. The calibration of structured-light 3-D measurement system[D].Hang Zhou：Zhejiang University，2013.

[5] 王中任，万仁全，刘亚俊. 基于最优匹配区域的结构光系统的投影仪标定[J]. 光学学报，2016，46(3)：37-43.

WANG Z R, WAN R Q, LIU Ya J.Projector calibration of structured light system based on optimal matching area[J]. Acta Optica Sinica，2016，46(3)：37-43.

[6] ZHANG.Z Y. A flexible new technique for camera calibration[J]. IEEE Journal of Pattern Anlysis and Machine Intelligence,2000,22(11):1330-1334.

[7] 张光澄．非线性最优化计算方法[M]．北京：高等教育出版社，2005.

[8] ZHANG．Z.TOWERS E，TOWERS D P．Simple calibration of a phase-based 3D imaging system based on uneven fringe projection[J]．Optics Letters，2011,36(5)：627-629．

[9] 王伟华，孙军华，刘震，等．钢轨磨耗动态测量结构光条纹中心提取算法[J]．激光与红外，2010,40(1):87-90.

WANG W H, SUN J H， LIU Z, et al. Stripe center extrication algorithm for structured-light in rail wear dynamic measurement[J]. Laser & Infrared，2010,40(1):87-90.