月地转移轨道中应急调整异面着陆场的轨道控制及优化方法

冯 飞，张雅声，张安理

0 引 言

近年来，针对月球两极地区，尤其是南极地区的探测任务已成为各主要航天国家或组织的研究重点[1-6].其中，载人月球探测返回任务对着陆场的气象水文条件有着较高要求，但月地间转移轨道飞行时间较长，不确定性因素较多.倘若航天器在完成月地轨道射入(trans-Earth injection，TEI)之后，主着陆场出现影响回收安全的恶劣天气状况，则必要时只能通过在转移过程中实施一定的轨道控制来实现对位于不同再入平面内的主、副着陆场的调整.Apollo-11在再入地球大气之前，因主着陆场上空出现台风，被迫在再入段将再入纵程从2 200 km调整到2 800 km，最终安全降落在副着陆场.由于受到航天器再入段的横程调节能力限制，这就要求主着陆场与副着陆场应近似位于同一再入平面内，太平洋广阔的海域为Apollo飞船通过再入纵程的调整来改变再入落区提供了可能，但这并不符合我国国情.位于四子王旗的主着陆场与位于酒泉的副着陆场地理经度间隔较大，并不在同一再入平面内，这就需要研究一种在月地转移段通过脉冲机动来调整终端再入轨道面的控制策略.国内外众多学者在轨迹优化及中途修正策略方面开展了研究.其中，张锦绣等[7]通过解析方法计算摄动下目标实际位置与二体情况下目标位置的偏差，提出了一种摄动下Lambert问题的解法；HUANG[8]提出一种主矢量近似方法，避开对动力学方程的简化，而是从主矢量方程入手，在航天器共面交会问题中得以应用；徐明等[9]针对设计出的3类中途修正策略，利用Monte-Carlo和遗传算法的联合仿真求得全局概率最优解，但其中Lambert转移轨道仅考虑了地球摄动；唐国金等[10]对航天器轨道优化理论进行了较为系统的研究.

本文结合实际任务，提出了一种月地引力场中求解Lambert问题的迭代方法，而后在转移轨道段施加双脉冲机动的控制策略，通过调整再入点位置，从而实现对非共面副着陆场的再入返回，并对该机动控制策略的能量最优解进行了研究及仿真验证.

1 着陆场应急调整策略及优化

本文称以主着陆场的终端再入条件为约束的返回轨道为原返回轨道，将轨道机动推力作用函数近似为脉冲函数，在副着陆场的终端再入条件下，可解算出一条新的月地返回轨道，称其为目标返回轨道.其中，月地转移轨道的计算方法见文献[11].则该任务中轨道调整的本质可等价为由原返回轨道机动至目标返回轨道的双脉冲交会问题，即Lambert问题，或两点边值问题.

1.1 全引力场Lambert问题求解方法

普适量解法是二体问题中求解Lambert问题的有效方法，但针对力学环境更加复杂的月地返回轨道而言，综合考虑多体引力及其非球形摄动等受力情况后，很难给出拉格朗日系数及其导数的解析形式.基于此，本文应用一种利用全引力场中的外推结果对二体Lambert解法进行修正的迭代算法[12]，通过较少次数的迭代即可求解出满足较高精度的在复杂引力场中的Lambert解.

设定全引力场模型为考虑地球引力体模型JGM3的21×21阶，月球引力体模型LP150Q的21×21阶，太阳引力模型按匀质球体计算.算法具体步骤描述如下：

(1)以新的再入终端约束条件为目标变量，计算得目标返回轨道.设两点P1、P2分别为原返回轨道与目标返回轨道上一点，在J2000.0惯性坐标系下的位置矢量分别为r1、r2，依据两点轨道历元之差，易知转移飞行时间；

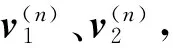
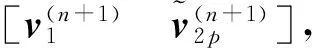
本文将STK与Matlab互联，在Matlab中实现Lambert问题的普适量解法，将计算结果作为初值写入STK中实现全引力场模型的轨道外推，再将外推结果返回Matlab继续计算.迭代算法计算流程见图1 所示.

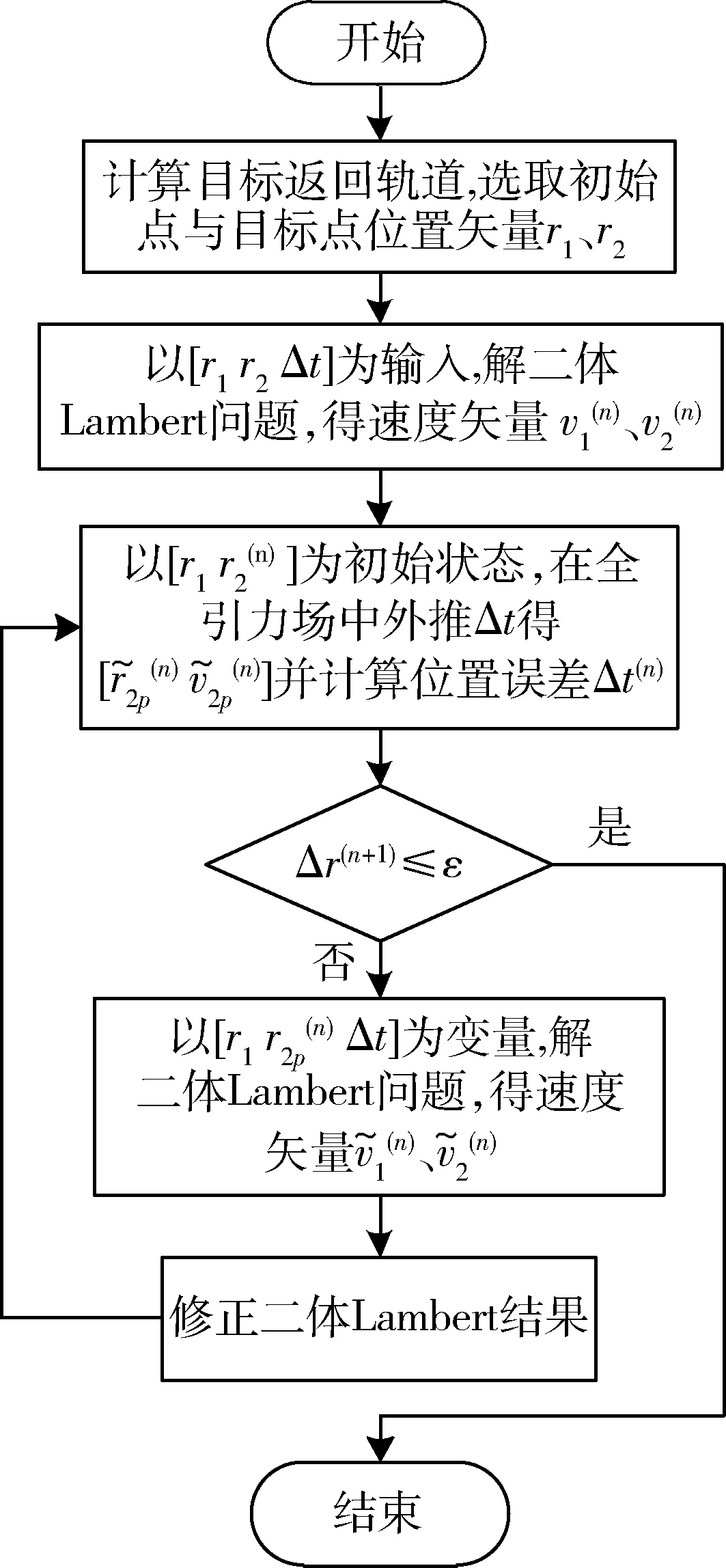
图1 全引力场中Lambert问题迭代算法流程图Fig.1 Flow chart of solving Lambert problem in a complete gravity field

1.2 轨道机动优化算法

在此任务中，轨道机动优化的实质为在何时、何处施加机动脉冲以保证能量最优的问题.其中，主矢量理论的判定条件与非最优主矢量理论相结合，可解决脉冲推力轨道机动的优化问题，但其弊端在于在每次脉冲推力的调整后，都需要人工对|λv|的曲线进行判定，效率不高.而模拟退火算法(SA)理论较为完善，其收敛性可以基于Markov过程进行分析，近年来在工程中得到了广泛应用.参考文献[13]的研究思路，本文结合最优的必要性判定条件、非最优主矢量改进措施以及模拟退火算法，应用一种交互式脉冲优化方法.

由最优控制理论，系统的哈密顿函数可描述为：

(1)

式中，λr、λv是r、v的协态变量.

哈密顿函数取极小值的必要条件为

(2)

由式(2)可得：

(3)

文献[14]提供了一种较为便捷的计算主矢量解析算法，描述如下：

(4)

Φp(t,t0)为主矢量的状态转移矩阵

Φp(t,t0)=N(t)N-1(t0)

(5)

N(t)、N-1(t)为

(6)

其中,r(t)、v(t)为参考脉冲轨道的解析表达式，为角动量矢量.其余变量表示如下：

(8)

(9)

式中，p、θ、e分别为轨道半通径、交会相位差及轨道偏心率.

(10)

此外，由Lion[15]等人发展的非最优主矢量理论进一步解决了如何把一条非最优脉冲参考轨道通过施加初始滑行段、终端滑行段以及中间脉冲的方式转变为最优脉冲轨道的问题，这里不再赘述.

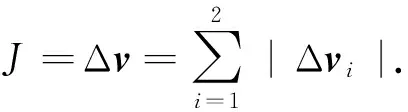
2 仿真分析

首先以文献[16]中计算的返回轨道为原返回轨道；相似地，以新的再入终端为约束条件，计算目标返回轨道，其月地转移轨道射入点与再入点轨道根数如表1中所示，参考系分别为月心惯性系与地心惯性系.酒泉副着陆场大地坐标为(41.12°N,100.32°E)，目标返回轨道再入点位置为(4.21°S,35.81°E)，地心段轨道倾角iE=43.4°，TEI时刻轨道历元2020年4月8日10:21:00 UTC，其余约束条件与原返回轨道一致.

图2 交互式最优求解流程Fig.2 Flow chart of the interactive optimization method

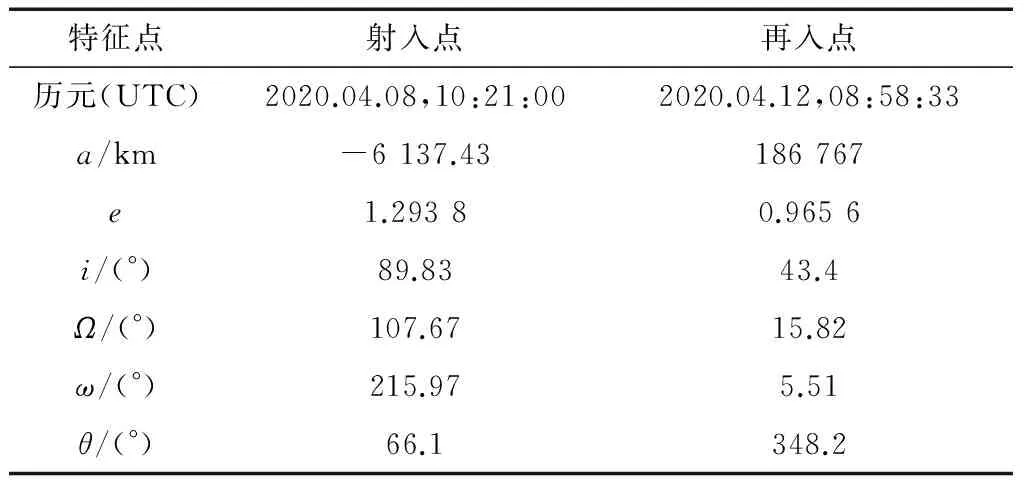
特征点射入点再入点历元(UTC)2020.04.08,10:21:002020.04.12,08:58:33a/km-6137.43186767e1.29380.9656i/(°)89.8343.4Ω/(°)107.6715.82ω/(°)215.975.51θ/(°)66.1348.2

脉冲时刻的值不易在邻近TEI时刻与终端再入时刻的区间内，其中，设定初始脉冲时刻与终端脉冲时刻的取值范围为2020 04 08 18:00:00～2020 04 12 00:00:00.

图3为非最优参考解的主矢量曲线，第一、第二脉冲时刻分别为2020 04 09 00:00与2020 04 10 12:00，总脉冲为0.04 km/s.

最优机动轨道主矢量计算结果如图4所示，脉冲最优解如表2所示.

由计算过程可知，本算例需两脉冲就可得到全局最优解，而无需增加中间脉冲.可见，最优解总脉冲大小为0.025 2 km/s，相比于参考解，最优解可以节省近一半的能量消耗.返回轨道机动全景仿真结果如图5～6所示，可以从星下点轨迹中看到再入点位置的变化情况，为返回至酒泉副着陆场，再入点经度西移了10.8°，轨道倾角由43.1°调整为43.4°.

图3 非最优参考解主矢量大小与时间关系Fig.3 The prime vector of reference results

图4 最优轨道主矢量大小与时间关系Fig.4 The prime vector of optimal results

脉冲时刻(UTC)2020,04,08,23:58:30.0002020.04,11,23:27:20.000Δv/(km/s)(-0.0104,-0.0074,-0.0023)(-0.0041,0.0109,0.0038)|Δv|/(km/s)0.0130.0122总脉冲/(km/s)0.0252

为进一步验证交互式最优方法的准确性，并更形象地说明施加脉冲时刻与速度脉冲大小的关系，做以下仿真：

(1)固定第一次脉冲时刻t0，则第一次脉冲在原返回轨道的位置r0(t0)也随即确定，以Δt为时间步长，分别计算交会点在目标返回轨道上的位置rf(t0+Δt×i)，计算每个交会位置对应的第一次转移速度脉冲、第二次转移速度脉冲与总速度脉冲.

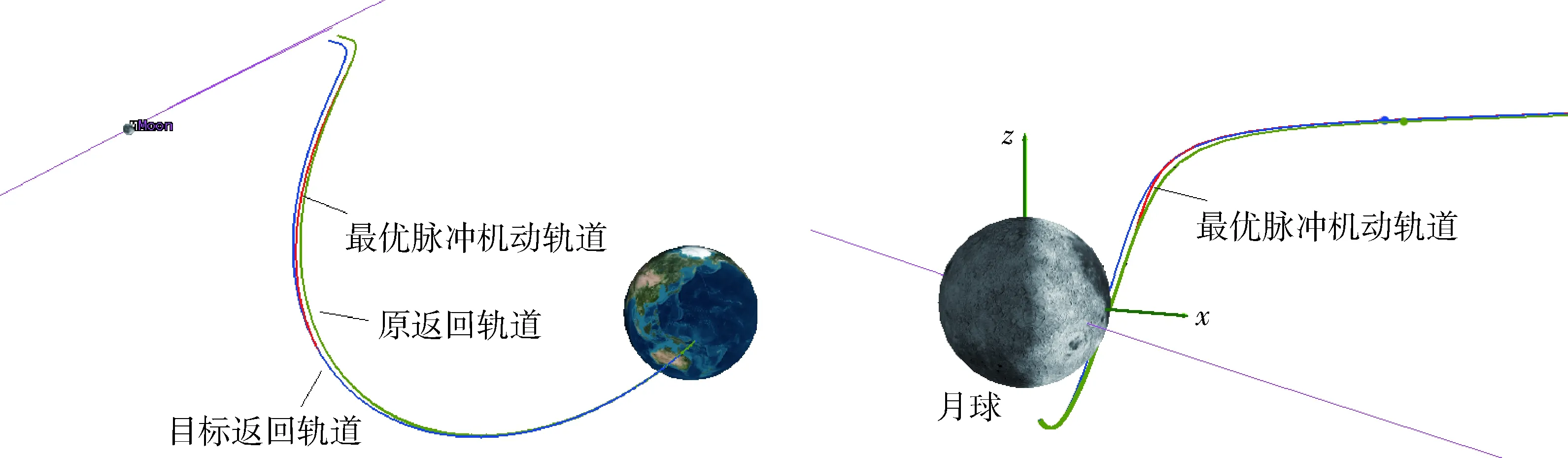
图5 最优脉冲机动轨道仿真全景图Fig.5 The simulations of optimal transfer trajectory

(2)固定第二次脉冲时刻tf，则交会点在目标返回轨道的位置rf(tf)也随即确定，以Δt为时间步长，分别计算第一次脉冲在原返回轨道上的位置r0(tf-Δt×i)，计算每个交会位置对应的第一次转移速度脉冲、第二次转移速度脉冲与总速度脉冲.

其中，Δt×i为脉冲转移时间，仿真设定Δt=2h，i=[1：40].仿真结果如图7～8所示.

图8 速度脉冲与第一次控制时间关系Fig.8 The relation between velocity pulse and the time of first impulse

可以看出，无论是固定第一脉冲位置或是第二脉冲位置，速度脉冲值的收敛值与交互式最优方法的结果十分相近.

3 结 论

本文以月球探测返回任务为背景，结合我国内陆着陆场的现状，提出了一种应急状况下，通过在月地转移轨道段实施双脉冲机动，以实现将航天器转移至再入平面以外的副着陆场的轨道机动策略，并应用一种交互式优化方法，结合仿真算例，得出了双脉冲条件下的能量最优解，仿真结果表明了该计算方法的有效性.值得说明的是，该落区调整策略不仅可用于月地转移轨道的前期设计与分析中，还可在诸如火星探测返回等其他行星探测返回任务中加以应用.但同时，应急情况本身就存在一定的随机性，工程中并不能够严格按照最优脉冲时刻实施变轨，这还取决于多种与优化本身无关的外界因素，例如主着陆场出现不利情况的时刻、决策响应时间等等.

参 考 文 献

[1] 冯飞,张雅声.多约束条件下月球南极探测返回窗口设计[J].空间控制技术与应用,2017, 43(3):21-27.

FENG F，ZHANG Y S.Design of Launch Window for Lunar South Pole Return Mission in Multi-Restrictions[J].Aerospace Control and Application,2017,43(3):21-27.

[2] CARPENTER J D,FISACKERLY R,DE ROSA D,et al.Scientific preparations for lunar exploration with the European Lunar Lander[J].Planetary and Space Science,2012, 74(1): 208-223.

[3] Russian Federal Space Agency. Russia space programs and exploration handbook[R].Moscow: Russian Federal Space Agency, 2011: 59.

[4] BENJAMIN V, DIEGO DE R,RICHARD F,et al.An analysis of illumination and communication conditions near lunar south pole based on Kaguya data[C]//Proceedings of the 7thInternational Planetary Probe Workshop.Washington D. C.:NASA,2010：1-7.

[5] COLAPRETE A,SCHULTZ P,HELDMANN J,et al.Detection of water in the LCROSS ejecta plume[J].Science,2010, 330(6003):463-468.

[6] WOODEN D H,COLAPRETE A,ENNICO K,et al.Lunar crater observation and sensing satellite (LCROSS) mission: results from the nadir near-infrared spectrometer aboard the Shepherding spacecraft[J].Lunarand Planetary Institute Science Conference Abstracts.41, 2010:2025-2026.

[7] 张锦绣,曹喜滨,张刘,等.J2项摄动下的Lambert问题算法研究[J].哈尔滨工业大学学报,2009(5):6-9.

ZHANG J X, CAO X B, ZHANG L, et al. An algorithm for Lambert solution based on J2 perturbation[J].Journal of Harbin Institute of Technology, 2009(5):6-9.

[8] HUANG W.Solving coplanar satellite rendezvous problem by primer vector approximation method[C]//AIAA/AAS Astrodynamic Specialist Conferences. Washington. D.C.: AIAA, 2012.

[9] 徐明,谭田,李志武,等.Lambert 转移中途修正的全局概率最优策略[J].北京航空航天大学学报,2012, 38(5): 574-578.

XU M, TAN T, LI Z W,et al.Optimal correction strategy during Lambert transfer from view of probability[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(5): 574-578.

[10] 唐国金，罗亚中，雍恩米.航天器轨道优化理论、方法及应用[M].北京：科学出版社，2011.

TANG G J, LUO Y Z, YONG E M. Trajectory optimization theory, method and application[M].Beijing:Science Press，2012.

[11] FENG F, ZHANG Y S.Application and analysis of an improved multiconic method in trajectory design of the lunar south pole return mission[J].Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2017:0954410017705896.

[12] 张磊,谢剑锋,刘勇.绕月返回飞行再入航程调整的轨道控制[J].飞行器测控学报, 2015,34(1):64-69.

ZHANG L, XIE J F, LIU Y.Trajectory maneuver for reentry downrange modification during circumlunar return flight[J].Journal of Spacecraft TT&C Technology,2015,34(1):64-69.

[13] LUO Y Z.Interactive optimization approach for optimal impulsive rendezvous using primer vector and evolutionary algorithms[J].ActaAstronautica,67(2):396-405.

[14] 罗亚中.空间最优交会路径规划策略研究 [D].长沙:国防科学技术大学,2007.

LUO Y Z.Study on Space Optimal Rendezvous Trajectory Planning Approach[D].Changsha:National University of Defense Technology, 2007.

[15] HANDELSMAN M,LION P M.Primer vector on fixed-time impulsive trajectories[J].AIAA Journal, 1968, 6(1): 127-132.

[16] 冯飞, 张雅声. 多约束条件下月球南极探测返回窗口设计[J].空间控制技术与应用, 2017, 43(3):21-27.

FENG F, ZHANG Y S.Design of Launch Window for Lunar South Pole Return Mission with Multi-Restrictions[J].Aerospace Control and Application,2017,43(3):21-27.