接触热阻对TPS法测量高聚物薄膜热导率的影响
2018-05-14张乃华李艳宁张国靖王雨薇
张乃华 李艳宁 张国靖 王雨薇


摘要:为研究接触热阻对瞬态平面热源(transient planesource,TPS)法测量高聚物薄膜热导率的影响规律以便提高测量准确度,阐述TPS法基本测量原理,根据串联热路中热阻的关系建立接触热阻的简化计算模型,以不同厚度硅橡胶薄膜为对象,通过回归分析的方法获得接触热阻随压力的变化规律,利用此规律测量单一厚度聚四氟乙烯薄膜和聚酯薄膜的热导率。结果表明:当未施加压力时,接触热阻的存在导致测量结果的相对误差为10%~30%,接触热阻会随压力的增大近似呈非线性关系减小,当压力达到200kPa时,可减小测量误差到6%以内。同种材质的高聚物薄膜还可通过改变厚度来减小接触热阻。
关键词:瞬态平面热源法;接触热阻;高聚物薄膜;热导率
文献标志码:A
文章编号:1674-5124(2018)02-0128-06
0引言
高聚物薄膜被广泛应用在化学化工、建筑节能、电子电气等不同领域。在这些领域的应用当中,热导率是评估此类薄膜散热或绝热能力的一个重要参数,例如燃料电池中气体扩散层、催化层的热导率测量有助于分析它们的热传递能力;建筑类高聚物薄膜热导率关乎着其节能性评价:集成电路中也需要已知导热性能的高聚物薄膜来保障电子元器件工作的可靠性。因此,高聚物薄膜热导率的准确测量已成为人们关注的热点。
目前,薄膜热导率的测量方法可以分为稳态法和瞬态法两大类。稳态法模型简单,操作方便,但所需时间长并且耗费能量多。瞬态法测量速度快,但理论模型复杂,主要有3法、激光脉冲法和瞬态平面热源法等。3法通过温度振幅随交流电频率的变化关系得到热导率,此法需要事先在被测样品表面镀上一根金属膜,操作复杂,一般用于带有衬底的半导体薄膜测量。激光脉冲法利用样品温度随时问的变化规律确定热扩散系数,进而得到热导率,此法需要配有激光器等高性能设备,而且要求样品不能透明以便于吸收激光。TPS法根据样品内部的温度响应,结合一维稳态传热模型得到热导率,现有的研究报道如:Gustavsson等对TPS法测量薄膜的理论进行了研究,利用方形探头测量了织物等薄膜的热导率;Zhang等对TPS法测量薄膜的准确度进行了数值模拟,并分析了理论与实际测量的差异:Kerr等基于TPS法测量了涂料纸的热导率。对于高聚物薄膜而言,由于其厚度极小,电气绝缘,无衬底,并且具有较高透明度,一般的薄膜测量方法已不再适用,而TPS法对样品的要求低,只需样品具有各向同性、表面平整的特点即可,因此该法适用于高聚物薄膜热导率的测量。
TPS法在测量高聚物薄膜热导率时会在串联热路中引入接触热阻。根据已有研究,接触热阻受温度、表面粗糙度以及壓力负载等诸多因素影响,而本文所测量高聚物薄膜具有表面光滑,厚度均匀的一般共性,表面粗糙度的差异不大并且对接触热阻影响很小,故在室温下压力才是最需要考量的外部因素。本文在阐述了TPS法基本测量原理的基础上,建立了接触热阻的简化计算模型,通过不同厚度硅橡胶薄膜的测量实验获得接触热阻随压力变化的经验公式,由此探讨接触热阻对热导率测量的影响,并根据总结出的规律测量单一厚度聚四氟乙烯薄膜和聚酯薄膜的热导率。
1TPS法测量薄膜热导率基本原理
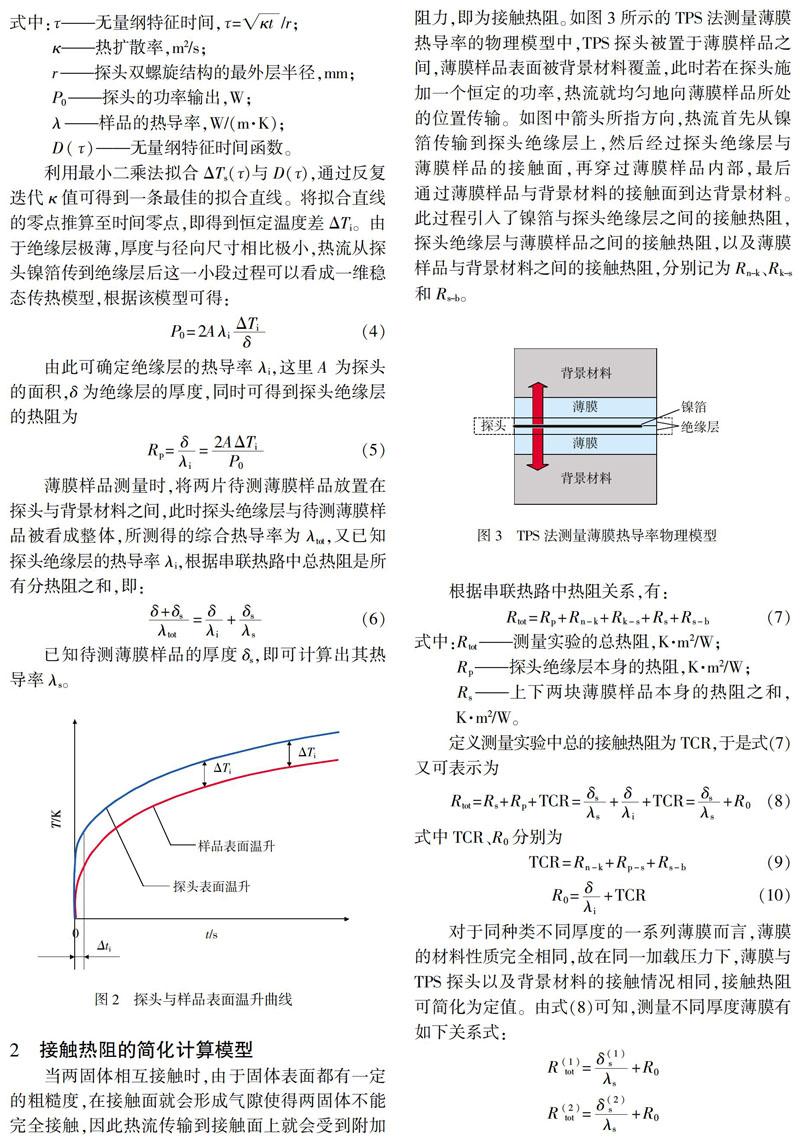
TPS法根据无限大介质中平面一维瞬态导热原理,在初始热平衡状态下,介质受到热源瞬态加热作用后产生温度场的变化,利用热传导过程中的温度数据与无量纲时间函数进行线性拟合,再结合一维稳态传热模型得到薄膜样品的热导率。该方法中的热源由图1所示的TPS探头提供,此探头包括蚀刻成双螺旋结构的镍箔和覆盖在表面的聚酰亚胺绝缘层。其中,镍箔不仅被用作热源将已知量的功率传递至样品,同时还作为电阻温度计来记录探头本身的温度增加。绝缘层可以保护镍箔不受外界破坏并使探头保持一定的机械强度。
3实验研究
3.1实验样品制备
选取4种不同厚度的硅橡胶薄膜,以及单一厚度的聚四氟乙烯和聚酯薄膜作为实验样品,硅橡胶薄膜厚度分别为0.17,0.24,0.31,0.43mm,聚四氟乙烯薄膜厚度为0.32mm,聚酯薄膜厚度为0.18mm。不同厚度硅橡胶薄膜加工工艺相同、材料性质完全一样,热导率标称值为0.24W/(m·K)。参照TPS法测量块状材料时对样品尺寸的规定:样品测试面有效直径不应小于探头直径的2倍,样品厚度应大于探头直径。故针对薄膜情况,制备的样品径向尺寸为60mmX60mm,背景材料整体尺寸为60mm×60mm×40mm。
3.2实验装置搭建
根据TPS法测量热导率的基本原理搭建了如图4所示的实验装置。该装置中TPS探头R与一个大功率精密标准电阻Rs串联,计算机控制的直流电源为探头提供恒定的加热功率。采用Agilent34410数字万用表作为高精度数据采集系统分别测量TPS探头与标准电阻两端的实时电压。计算机通过上位机软件控制TPS探头的加热时间、加热功率等实验参数,同时将采集到的电压数据进行计算得到温升曲线,最后经过分析得到实验结果。
考虑到薄膜热导率由一维稳态导热定律得到,实验过程中应使薄膜样品表面受热尽量均匀,故选择镍箔宽度为0.8mm,间距为0.2mm,半径为14mm的TPS探头。根据ISO/FDIS 22007-2——2014规定,TPS法测量薄膜热导率时应选择热导率大于薄膜热导率10倍以上的背景材料,一般推荐皂石和不锈钢。而皂石比不锈钢硬度小,表面更为光滑,更容易与薄膜样品充分接触,因此选择热导率为6.5W/(m·K)的皂石作为背景材料。实验前将探头夹在两块完全相同的样品之间形成三明治结构,再将三者置于两块皂石之间,并在皂石上表面安装好压力加载装置。
3.3实验结果与分析
设置好合适的测量参数后,利用搭建好的实验装置对4种不同厚度的硅橡胶薄膜进行了多次测量,在实验过程中改变加载在背景材料上的压力大小,得到总热阻测量值如图5所示。从图中可以看出,相同压力下总热阻Rtot随厚度δ的变化近似呈线性关系。分别对30,60,90,120,150,180kPa压力条件下的Rtot与δ进行线性拟合,所得线斜率、截距和线性相关系数如表1所示。由表中数据可知,不同压力下的拟合结果线性度良好,斜率趋于一致,截距随着压力增大而减小。
利用Rtot与δ线性拟合的截距可计算出不同加载压力下接触热阻如图6所示。当背景材料上的加载压力为30kPa时,总的接触热阻约为0.36×10-3K·m2/W,并且随着压力的增大,接触热阻急剧减小。尤其当压力从30kPa增加为60kPa时,接触热阻变化显著。原因可能是较小的压力下,探头、薄膜以及背景材料三者之间并未紧密接触,此时压力可以较大程度上减小接触热阻。然而当压力大于180kPa时,接触热阻的变化趋势很小,此时压力的增大已经很难更大程度上减小接触热阻。根据图中接触热阻随压力的变化关系,可建立接触热阻TCR与压力p的回归模型为TCR=b+a/p,其中a为回归系数,b为常系数。通过回归分析可得参数a=0.07477,b=8.73084。该回归模型的相关系数R2为0.98667,表明其具有较好的拟合程度。由此得到在加载压力为0-200kPa条件下,测量硅橡胶薄膜时接触热阻TCR随压力p变化的经验公式为:TCR=0.07477+8.73084/p。
利用Rtot与δ线性拟合的斜率可计算出硅橡胶膜热导率为0.254W/(m·K),相对误差为5.8%。另外,将不同厚度硅橡胶膜分开测量,所测得的硅橡胶薄膜热导率的相对误差如图7所示。由此看出,当未施加压力时,热导率与标称值相比偏小10%-30%,而且在相同压力下,厚度越小的薄膜热导率相对误差反而越大,随着压力的增大,不同厚度薄膜的热导率相对误差都逐渐减小,直到压力为200kPa时,相对误差减小到6%以内。结合接触热阻的分析可知,在较小的加载压力下,厚度越小的薄膜测量中的接触热阻所占薄膜本身热阻的比例更大,从而对热导率测量结果造成更大的误差。
从以上分析可知,选择不同厚度的高聚物薄膜和改变加载压力这两种方法均可减小接触热阻。然而当待测高聚物薄膜只有一种厚度时,改变加载压力才是最有效的方法。参照硅橡胶薄膜测量时接觸热阻随压力的变化规律,若压力为200kPa,回归模型可预测出接触热阻为0.118×10-3K·m2/W,在此条件下测量单一厚度的聚四氟乙烯薄膜和聚酯薄膜的热导率,结果如表2所示。从表中看出,此压力条件下,两种高聚物薄膜测量结果的相对误差都在6%以内。
4结束语
本文根据串联热路中热阻的关系建立了接触热阻的简化计算模型,选择同种材质不同厚度的硅橡胶薄膜进行实验,通过改变厚度和改变压力对其热导率进行测量,从中获得接触热阻的影响规律,并根据此规律测量了聚四氟乙烯薄膜和聚酯薄膜的热导率,得到的结论如下:
1)利用TPS法测量高聚物薄膜时,接触热阻会对测量结果造成较大误差,而且厚度越小的高聚物薄膜,所受影响越大。接触热阻会随压力的增大近似呈反比例函数的关系减小。
2)可以通过改变厚度和改变加载压力两种方法来减小接触热阻的影响。然而前者只适用于各项材质相同,并且易于获得不同厚度的高聚物薄膜,对于单一厚度的高聚物薄膜而言,只能加载更大的压力。一般在200kPa的压力条件下,测量结果的误差会减小到6%以内。
