《一次函数的图象及其性质 人教版初中数学八年级下册19.2.2.》教学案例
2018-05-14雷建金
雷建金
教学目标:
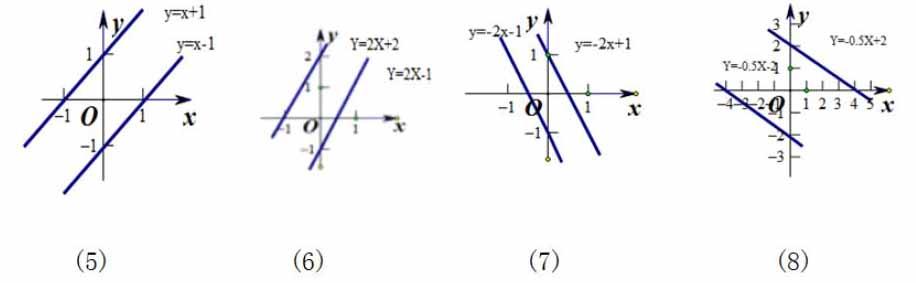
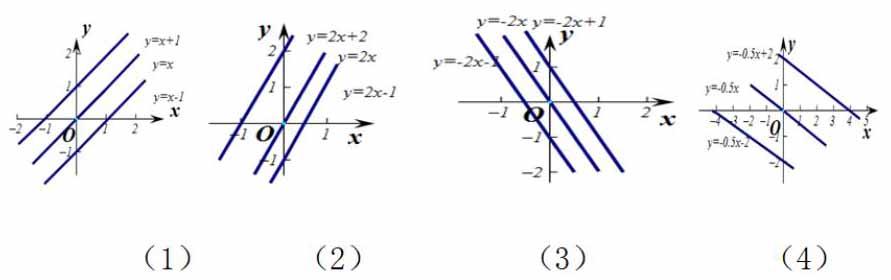
1.会画一次函数的图象,能根据一次函数图象和表达式y=kx+b(k≠0)探索并理解k>0和k<0时图象变化情况。从而理解函数的性质。
2.提高学生的思维能力、分析问题及解决问题的能力,合情推理能力及发现新知识新问题的能力。
3.培养学生学习数学的兴趣和积极性。
教学重点:一次函数的图象和性质
教学难点:探索k值的符号对图象的影响及k,b的符号决定图象的位置。
教学过程:
活动五 自主小结,自我评价
本节课你的收获是什么?在学会学习方面学会了什么?
可以引导学生从知识与技能、思考与能力、情感与态度、思想与方法等方面小结。
案例设计说明:
设计的理念是把课堂还给学生,通过学生自主学习、合作学习,主动地积极地去建构知识,达到学会学习的目的。
自主学习立足于学生先想先做,根据自己的认知、体验、思维方式进行自主探索,独立思考。活动一、活动四、活动五就是自主复习、自主练习、自主小结。自主复习,旧知识得到深化;自主练习,新知识得到反馈与评价;自主小结,学生在知识、能力、思想、方法情感等方面形成本节的知识体系。
合作学习是小组中承担共同任务,且有责任分工的一种互助性学习。案例中活动二、活动三就是合作学习的,其内容是一次函数的图象和性质,这既是本节的重点也是难点,采用小组合作的方法是让学生在学习中主动交流,大胆展示,既要展示自己在学习中的经验、体会、困难及存在的问题,也要帮助组内有困难的同学解决问题,还要认真聆听同学的见解和老师的引导,最终是学好一次函数的图象和性质。学习金字塔理论告诉我们自主学习、合作学习、教他人学习是最优效的学习方法,巩固率达90%左右。
案例中一次函数的图象和性质这些新的知识,学生都经历了它的形成与发生过程,是经过作图、观察、比较、分析、猜想、填空、验证、归纳等活动来探索出来的,如一次函数的图象,表达式y=kx+b(k≠0)中常数k,b的意义,还有直线y=kx(k≠0)与直线y=kx+b(k≠0)的位置關系,一次函数的性质。这些都有助于发展学生的合情推理能力。
案例采用了开放型的设计,活动一的第二个问题,活动三的第二个问题都是开放型的问题,这对于培养学生发散思维、创新意识和精神具有很好的作用。
教学设计中,活动都是由学生来完成的,这体现了学生在学习活动中的主体地位。即主体原理。教师成了课堂教学的组织者、合作者、指导者、评价者。
案例用计算机作为辅助性教学,大大地提高了教学效率。
