再装条款下基于效用无差别方法的经理股票期权定价

傅毅 张寄洲 吉素蕾

摘要：

“不可交易”是经理股票期权（ESO）的重要特征之一.受制于此，经理股票期权无法通过对冲其标的资产来完成定价.考虑一类具有再装条款的经理股票期权，基于效用无差别方法，运用随机控制理论，推导出了定价模型满足的Hamilton-Jacobi-Bellman（HJB）方程，并运用格林函数，计算得到了经理股票期权无差别价格的解析解.最后，对模型的解析解进行了参数分析.

关键词：

经理股票期权（ESO）; Hamilton-Jacobi-Bellman（HJB）方程; 效用无差别定价; 格林函数

中图分类号： O 175.2文献标志码： A文章编号： 1000-5137（2018）01-0001-10

Utility indifference pricing of ESO with reload terms

Fu Yi1， Zhang Jizhou1*， Ji Sulei2

（1.School of Finance and Business，Shanghai Normal University，Shanghai 200234，China;

2.Mathematics and Science College，Shanghai Normal University，Shanghai 200234，China）

Abstract：

″Nontradable″ is one of the important characters of the Executive Stock Option（ESO）.Therefore，the ESO cannot be priced by hedging the corresponding underlying asset.In this paper，we study ESO with reload terms by utility indifference method，based on stochastic control theory.We deduce the Hamilton-Jacobi-Bellman（HJB） equation of the pricing model.Using variable substitution and Green function method，we obtain its analytic solution.Finally，we analyze the parameters of the model.

Key words：

executive stock option（ESO）; Hamilton-Jacobi-Bellman（HJB） equation; utility indifference pricing; Green function

收稿日期： 2017-02-20

基金項目： 国家自然科学基金（71471117）;上海市教委科研创新重点项目（13ZZ107）;上海师范大学自科项目（SK201506）;教育部人文社会科学研究青年基金（17YJCZH044）

作者简介： 傅毅（1981-），男，副教授，主要从事金融数学方面的研究.E-mail：fuyi@shnu.edu.cn

*通信作者： 张寄洲（1958-），男，教授，主要从事金融数学方面的研究.E-mail：zhangjz@shnu.edu.cn

引用格式： 傅毅，张寄洲，吉素蕾.再装条款下基于效用无差别方法的经理股票期权定价 [J].上海师范大学学报（自然科学版），2018，47（1）：1-10.

Citation format： Fu Y，Zhang J Z，Ji S L.Utility indifference pricing of ESO with reload terms [J].Journal of Shanghai Normal University（Natural Sciences），2018，47（1）：1-10.

0引言

经理股票期权（ESO）是一种基于业绩的报酬激励机制，其实质是给予经理人一定的企业所有权和剩余索取权，将经理人的报酬与企业的长期发展业绩或者某些长期财务指标密切联系在一起，以有效地解决经理层长期激励不足的问题.自20世纪70年代以来，经理股票期权被越来越多的国家广泛应用.在美国，根据Hall和Murphy[1]的调查，1994年在标准普尔指数的500个参考公司中，94%的公司授予其经理人股票期权.股票期权占高级经理人员年收入的比重也越来越高，美国前200家大企业首席执行官的平均现金年薪略高于75万美元，但仅靠股票期权，1998年每位首席执行官的平均现金年薪税前收入约达830万美元.

在我国，据中国企业联合会和中国企业家协会的调查表明：82.64%的国企经营者认为影响我国企业经营者队伍建设的主要因素是“激励不足”.因此，近年来，我国上市公司也开始引入经理股票期权激励制度.2005年底中国证监会发布了的《上市公司股权激励管理办法》，次年9月，国资委与财政部联合发布了《国有控股上市公司实施股权激励试行办法》.2006年中捷股份成为中国第一家实施了真正意义上的股票期权激励计划的企业.根据数据库的资料显示，从2006年到2014年间，我国约有610家上市公司先后实施了股权激励计划，其中342家采用的是股票期权的方式，占比为56%;剩下的268家采用的是限制性股票和股票増值权两种方式，可以看出在所有的股权激励方式中，股票期权是运用最普遍的一种方式.与普通欧式期权不同，若要对经理股票期权定价，还需要考虑其自身的几个重要特征.

Cov（dω（1）u，dω（2）u）=ρ du（0≤ρ≤1）.

假设3：投资者效用假设

本研究选用的效用函数为指数效用函数：

U（x）=-e-γ x，

其中x ∈R，γ>0，这个效用函数称为常数完全厌恶（CARA）效用函数，即风险厌恶系数γ=-U″（x）U′（x）为常数.风险厌恶系数的大小反应了投资者对待风险的态度，即风险厌恶程度.对同一水平的风险，投资者的γ越大，越厌恶风险，即要求的风险回报越高.

假设4：交易策略假设

令经理人的初始财富为x，财富控制过程为πu，其表示在[t，T]期间投资在市场指数的头寸数量.财富控制过程πu是Fu-可测的，且满足E∫T0πu2du<∞，即πu为可容许的.定义Πt，T为这些所有可容许交易策略所构成的空间.

2再装条款下的经理股票期权定价模型建立

由前文关于效用无差别价格方法的介绍可知，要求出一份经理股票期权的效用无差别价格，实际上需要分别在投资者持有或不持有经理股票期权这两种情况下，实现投资者在到期日T时刻的期望效用最大化.所谓的无差别价格就是让这两个值函数相等的期权的价格.因此，求解效用无差别价格就需要求解两个投资组合的最优化问题.

首先，考虑第一个投资组合的最优化问题（Merton问题），也就是经理人只投资于市场指数和银行账户.那么对于u∈[t，T]，经理人的资产投资财富变化过程Xu满足：

dXu=[rXu+πu（μp-r）]du+σpπudω（2）u.（3）

引理1

若经理人只将财富x投资于市场指数和银行账户中时，则经理人的资产在T时刻的期望最大效用的值函数M（x，t）为：

M（x，t）=supΠt，TE{-e-γ XT| Xt=x}，=-exp-γ xer（T-t）-θ2p2（T-t），（4）

其中θp=μp-rσp为市场指数的夏普比率.

证明：由动态规划原理可知，值函数M（x，t）满足的HJB方程为：

Mt+[（μp-r）π+rx]Mx+12σ2pπ2Mxx=0，（5）

先对其两边求导，求得HJB方程的最优控制

π*=argmax12σ2pπ2Mxx+（μp-r）π Mx，=-θpMxσpMxx，

其中θp=μp-rσp.将π*代入（4）式得

MtMxx-θ2p2Mx2+rx MxMxx=0，（6）

为了进一步简化方程，在对变量进行变换，令x—=xer（T-t），则（6）式可简化为

MtMxx-θ2p2Mx2=0.

由于本研究是指数效用函数下的定价问题，故考虑方程解的形式为M（x，t）=-exp{-γ（x—+w（t））}.容易验证w（t）满足以下常微分方程

w′t-θ2p2=0.

再考虑边界条件w（T）=0，即可求得w（t）=θ2p2（T-t），将所有原变量代回，得Merton问题的解为

M（x，t）=-exp-γ xer（T-t）-θ2p2（T-t）.

下面考虑第二个投资组合的最优化问题，即经理人将财富x投资于3种资产中：经理股票期权、市场指数以及银行账户.为了对这一问题进行建模，首先考虑经理股票期权在到期日的收益，即经理股票期权一旦被再装，经理人将得到1-1h份的股票和1h份交割价为hK，到期日仍为T的新期权.故在T时刻经理股票期权的收益为：（ST-K ）+1{ τ ≥T}+hK-K+1h（ST-hK ）+1{τ < T}.至此，可得投资组合的值函数为：

V（x，s，t）=supΠt，TEUXT+（ST-K）+1{τ ≥T}+hK-K+1h（ST-hK）+1{τ < T}.（7）

在给出两类效用最大化问题后，运用效用无差別定价的原理可以给出经理股票期权的无差别价格的如下定义.

定义1

经理股票期权的无差别价格g（s，t）为以下方程的解：

V（x-g（s，t），s，t）=M（x，t）.（8）

因此，经理股票期权的无差别价格，实际上就转化为值函数V（x，s，t）.首先，先将上述问题转化为对应的HJB方程.

引理2

由动态规划原理及Ito^公式，值函数（7）满足的HJB方程及边界条件为：

supΠt，TLV（x，s，t）=0，（x，s，t）∈R×（0，hK]×[0，T），

V|s=hK=-exp{-γ er（T-t）（x+hK-K）}，（x，t）∈R×[0，T]，

V|t=T=-exp{-γ（x+（s-K）+）}，（x，s）∈R×（0，hK]，

（9）

其中LV=Vt+12σ2pπ2Vxx+12σ2ss2Vss+ρπσpσssVxs+[π（μp-r）+rx]Vx+μssVs.

证明：由动态规划原理可知，对 h∈[0，T-t]有

V（x，s，t）=supΠt，TE[U（XT，ST，）|Xt=x，St=s]，=supΠt，TE[V（Xt+h，St+h，t+h）|Xt=x，St=s]，

则V（x，s，t）≥qE[V（Xt+h，St+h，t+h）|Xt=x，St=s].两边同时减去V（x，s，t），乘以1h，再取极限得

0≥q limh0E[（V（Xt+h，St+h，t+h）-V（x，s，t））|Xt=x，St=s]，（10）

由Ito^公式可得

V（Xt+h，St+h，t+h）=V（x，s，t）+∫t+htLπV（Xu，Su，u）du+∫t+htσsSuVsdω（1）u+σpπuVxdω（2）u，

其中LπV=Vu+12σ2pπ2Vxx+12σ2ss2Vss+ρπσpσssVxs+[π（μp-r）+rx]Vx+μssVs.至此，（10）式可转化为LπV（x，s，t）≤0，并进一步得到

supΠt，TLπV（x，s，t）≤0.（11）

此外，若π*为最优控制过程，则对 h∈[0，T-t]有V（x，s，t）=E[V（X*t+h，S*t+h，t+h）|Xt=x，St=s]，即

Lπ*V（x，s，t）=0，（12）

由（11）和（12）式可知

supΠt，TLπV（x，s，t）=0.

3再装条款下的经理股票期权定价模型求解

在此将对上述建立的HJB方程进行求解.首先解得效用最大化问题（9）式的最优控制为：

π * argmax12σ2Pπ2Vxx+（ρσpσssVxs+（μp-r）Vx）π=-ρσpσssVxs+（μp-r）Vxσ2pVxx.

（13）

将最优控制π*（13）式代入算子L得到如下方程：

VtVxx+12σ2ss2（VssVxx-ρ2V2xs）-12θ2pV2x-ρθpσss VxVxs+μss VsVxx+rx VxVxx=0，（14）

其中θp=μp-rσp为市场指数的夏普比率.

令x—=xer（T-t），可得Vt=Vt-rx—Vx—，Vx=er（T-t）Vx—，Vxx=e2r（T-t）Vx—x—，Vxs=er（T-t）Vx—s.

那么（14）式可变换为：

VtVx—x—+12σ2ss2（VssVx—x—-ρ2Vx—s2）-12θ2pVx—2-ρθpσssVx—Vx—s+μssVsVx—x—=0.（15）

由于选用的是指数效用函数，故考虑方程解的形式为V（x—，s，t）=-exp{-γ（x—+W（s，t））}.

容易验证W（s，t）满足以下半线性偏微分方程：

Wt+12σ2sss2Wss+（μs-ρθpσs）sWs+12γ（ρ2-1）σ2ss2W2s+θ2p2γ=0，（16）

为了简化（16），并对其求解，对半线性偏微分方程做如下变换：W（s，t）=1γ（ρ2-1）lnC（s，t），则Wt=1γ（ρ2-1）·CtC，Ws=1γ（ρ2-1）·CsC，Wss=1γ（ρ2-1）·CCss-C2sC2.

那么（16）式变换为：

Ct+12σ2ss2Css+（μs-ρθpσs）sCs+12（ρ2-1）θ2pC=0.（17）

引理3

经过以上变换，C（s，t）为以下终边值问题的解：

L′C（s，t）=0，（s，t）∈（0，hK]×[0，T），

C|s=hK=exp{γ（ρ2-1）（hK-K）er（T-t）}，t∈[0，T]，

C|t=T=exp{γ（ρ2-1）（s-K）+}，s∈（0，hK].

（18）

其中L′C=Ct+12σ2ss2Css+（μs-ρθpσs）sCs+12（ρ2-1）θ2pC.

为了求得方程（18）式的解，需要先求解C（s，t）关于算子L′的格林函数.为此，先给出以下引理.

引理4

在区间R+×[0，T]上，C（s，t）关于算子L′的格林函数为：

G（s，t;ξ，T）=exp-12（1-ρ2）θ2p（T-t）ξσs2π（T-t）exp-lnsξ+A（T-t）22σ2s（T-t）×

1-exp2lnhKξlnshKσ2s（T-t），（19）

其中A=μs-ρθpσs-12σ2s.

证明：设算子L′的基本解为G（s，t;ξ，T），由基本解的定义知：

L′G（s，t;ξ，T）=0，（s，t）∈（0，hK]×[0，T），

G|s=hK=0，t∈[0，T]，

G|t=T=δ（s-ξ），s∈（0，hK].

（20）

作變换y=lnsξ，τ=T-t，则

Gτ-12σ2s2Gy2-AGy+12（1-ρ2）θ2pG=0，（y，τ）∈-∞，lnhKξ×（0，T]，

G|y=lnhKξ=0，τ∈[0，T]，

G|τ=0=1ξδ（y），y∈-∞，lnhKξ.

其中A=μs-ρθpσs-12σ2s.为了简化方程，作进一步变换，令 G（y，τ;ξ，T）=eατ+β yU（y，τ;ξ，T），其中α，β满足α=-A22σ2s-12（1-ρ2）θ2p，β=-Aσ2s.那么，上述的定解问题（20）就转换为：

Uτ-σ2p22Uy2=0，（y，τ）∈-∞，lnhKξ×（0，T]，

U|y=lnhKξ=0，τ∈[0，T]，

U|τ=0=1ξδ（y）， y∈-∞，lnhKξ.

令y—=y-lnhKξ，则y—∈（-∞，0]，再利用镜像法，可得：

Uτ-σ2p22Uy—2=0，（y—，τ）∈R×（0，T]，

U|τ=0=1ξδy—+lnhKξ-1ξδy—-lnhKξ，y—∈R.

至此，得到了一个标准的热传导方程，其解为：

U（y，τ）=1ξσs2πτexp-y—+lnhKξ22σ2sτ-exp-y—-lnhKξ22σ2sτ.

将变量代回，得到C（s，t）关于算子L′的格林函数为：

G（s，t;ξ，T）=exp-12（1-ρ2）θ2p（T-t）ξσs2π（T-t）exp-lnsξ+A（T-t）22σ2s（T-t）×1-exp2lnhKξlnshKσ2s（T-t）.

运用以上获得的格林函数便可得方程（18）的解，即为如下引理.

引理5

偏微分方程（18）的解为：

C（s，t）=∫hK0exp{γ（ρ2-1）（ξ-K）+G（s，t;ξ，T）}dξ

-σ2s2∫Ttexp{γ（ρ2-1）（hK-K）er（T-η）}（ξ2G）ξξ=hKξ=0 dη.（21）

证明：用G^（ξ，η;s，t）表示方程（18）式的共轭方程的解，则

L^′G^（ξ，η;s，t）=0，（ξ，η）∈[0，hK]×[t，T），

G^|ξ=hK=0，η∈[t，T]，

G^|η=t=δ（ξ-s），s∈[0，hK].

其中L^′G^=-G^ηG^+12σ2s2ξ2（G^ξ2）-（μs-ρθpσs）ξ（G^ξ）-12（1-ρ2）θ2p.先考虑积分

0=∫hK0dξ∫T-t+[G^（ξ，η;s，t）L′C（ξ，η）-C（ξ，η）L^′G^（ξ，η;s，t）]dη

=∫hK0dξ∫T-t+G^（ξ，η;s，t）Cη+12σ2sξ2Cξξ+（μs-ρθpσs）ξ Cξ+12（ρ2-1）θ2pC

-C（ξ，η）-G^η+12σ2s2ξ2（G^ξ2）-（μs-ρθpσs）ξ（G^ξ）-12（1-ρ2）θ2pG^dη

=∫hK0dξ∫T-t+η（G^C）+σ2s2ξξ2G^Cξ-12ξCξ（ξ2G^）

+（μs-ρθpσs）ξ（ξG^Cdη

=∫hK0（G^C）η=T-η=t+dξ+σ2s2∫T-t+ξ2G^Cξξ=hKξ=0dη

-σ2s2∫T-t+Cξ（ξ2G^）ξ=hKξ=0dη+（μs-ρθpσs）∫T-t+（ξG^C）ξ=∞ξ=hKdη

=I1+I2+I3+I4，

令ε0，則

I1=∫hK0（G^C）η=Tη=tdξ=∫hK0[G^（ξ，T;s，t）C（ξ，T）-G^（ξ，t;s，t）C（ξ，t）]dξ

=∫hK0exp{γ（ρ2-1）（ξ-K）+}G^（ξ，T;s，t）dξ-C（s，t），

I2=σ2s2∫Ttξ2G^Cξξ=hKξ=0dη=0，

I3=-σ2s2∫TtCξ（ξ2G^）ξ=hKξ=0dη =-σ2S2∫Ttexp{γ（ρ2-1）（hK-K）er（T-η）}ξ（ξ2G^）ξ=hKξ=0dη，

I4=（μs-ρθpσs）∫Tt（ξG^C）ξ=hKξ=0dη=0.

由此可得

C（s，t）=∫hK0exp{γ（ρ2-1）（ξ-K）+}G^（ξ，T;s，t）dξ

-σ2s2∫Ttexp{γ（ρ2-1）（hK-K）er（T-η）}（ξ2G^）ξξ=hKξ=0dη.

又因为G^（ξ，T;s，t）=G（s，t;ξ，T），所以结论得证.

下面将给出本研究的主要结果，即经理股票期权的无差别价格的定价公式.

定理1

若再装条款下的经理股票期权满足本文的假设1～4，则该期权的无差别价格g（s，t）为

g（s，t）=e-r（T-t）γ（ρ2-1）lnC（s，t）-12（ρ2-1）θ2p（T-t）.

（22）

证明：由经理股票期权的无差别价格的定义知，经理股票期权的无差别价格h（s，t）满足以下方程

V（x-g（s，t），s，t）=M（x，t），（23）

由V（x，s，t）与C（s，t）的转换关系可知：

V（x，s，t）=-exp-γx er（T-t）+1γ（ρ2-1）lnC（s，t），

所以，（23）式等价于

-exp-γ（x-g（s，t））er（T-t）+1γ（ρ2-1）lnC（s，t）=-exp-γ xer（T-t）-12θ2p（T-t）.

再由引理5即可得到经理股票期权的无差别价格

g（s，t）=e-r（T-t）γ（ρ2-1）lnC（s，t）-12（ρ2-1）θ2p（T-t）.

得证.

4效用无差别定价的参数分析

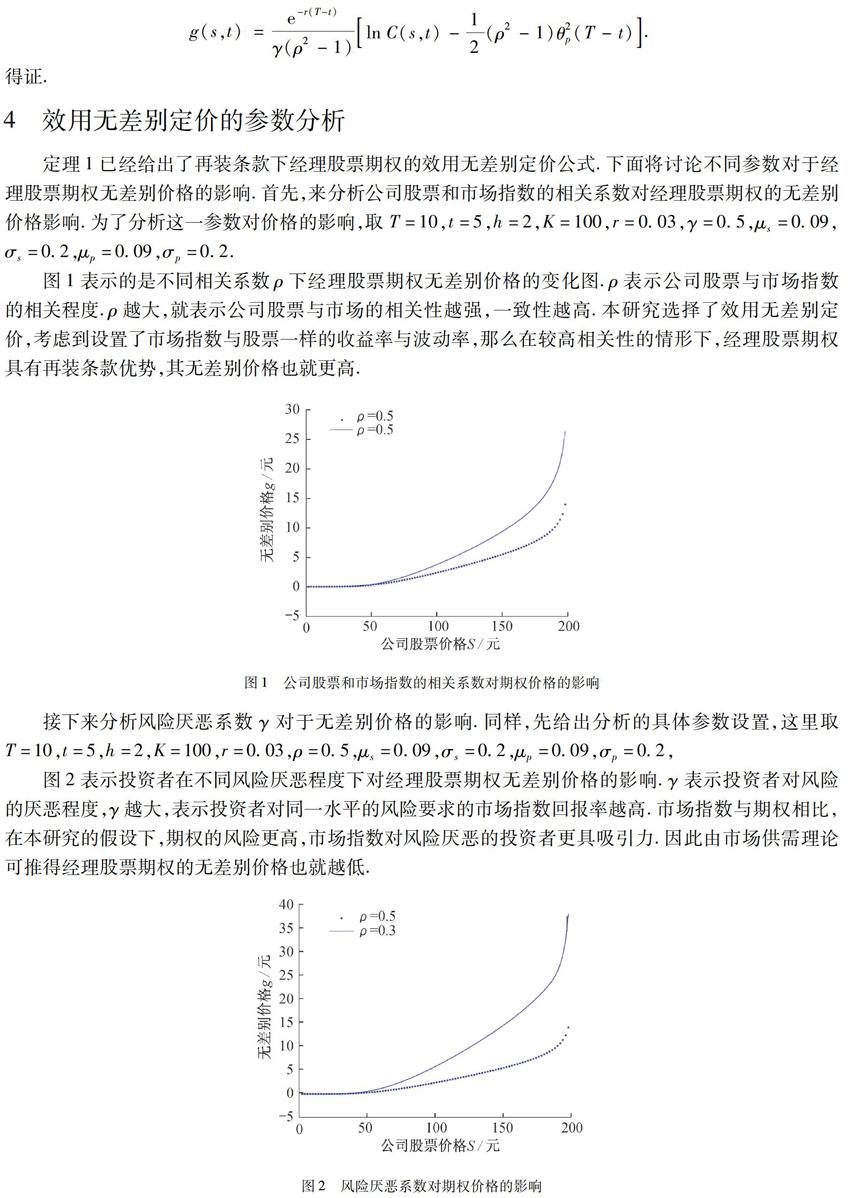
定理1已经给出了再装条款下经理股票期权的效用无差别定价公式.下面将讨论不同参数对于经理股票期权无差别价格的影响.首先，来分析公司股票和市场指数的相关系数对经理股票期权的无差别价格影响.为了分析这一参数对价格的影响，取T=10，t=5，h=2，K=100，r=0.03，γ=0.5，μs=0.09，σs=0.2，μp=0.09，σp=0.2.

图1表示的是不同相关系数ρ下经理股票期权无差别价格的变化图.ρ表示公司股票与市场指数的相关程度.ρ越大，就表示公司股票与市场的相关性越强，一致性越高.本研究选择了效用无差别定价，考虑到设置了市场指数与股票一样的收益率与波动率，那么在较高相关性的情形下，经理股票期权具有再装条款优势，其无差别价格也就更高.

图1公司股票和市场指数的相关系数对期权价格的影响

接下来分析风险厌恶系数γ对于无差别价格的影响.同样，先给出分析的具体参数设置，这里取T=10，t=5，h=2，K=100，r=0.03，ρ=0.5，μs=0.09，σs=0.2，μp=0.09，σp=0.2，

图2表示投资者在不同风险厌恶程度下对经理股票期权无差别价格的影响.γ表示投资者对风险的厌恶程度，γ越大，表示投资者对同一水平的风险要求的市场指数回报率越高.市场指数与期权相比，在本研究的假设下，期权的风险更高，市场指数对风险厌恶的投资者更具吸引力.因此由市场供需理论可推得经理股票期权的无差别价格也就越低.

圖2风险厌恶系数对期权价格的影响

5结论

在效用无差别的框架下，基于经理股票期权“不可交易”的基本特征建立了具有再装条款的经理股票期权定价模型，运用格林函数，计算得到了模型对应HJB方程的解析解.最后，对模型的参数进行了比较分析.该结果将有助于进一步完善我国职业经理人薪酬制度和会计处理方法，提高我国企业职业经理人激励的管理水平.

参考文献：

[1]Hall B J，Murphy K J.Stock options for undiversified executives [J].Journal of Accounting and Economics，2002，33（1）：3-42.

[2]Carmona J，Leon A，Vaello-Sebastia A.Pricing executive stock options under employment shocks [J].Journal of Economic Dynamics and Control，2011，35（1）：97-114.

[3]Hsiao Y L.A simple method to price window reset options [J].Journal of Mathematical Finance，2013，3（1）：96-102.

[4]Wu M C，Lin I.Determining fair values of performance-vested and forfeiture-embedded employee stock options [J].Accounting and Finance，2013，53（4）：1083-1106.

[5]Song D，Yang Z.Utility-based pricing，timing and hedging of an american call option under an incomplete market with partial information [J].Computational Economics，2014，44（1）：1-26.

[6]Kyng T，Konstandatos O，Bienek T.Valuation of employee stock options using the exercise multiple approach and life tables [J].Insurance：Mathematics and Economics，2016，68：17-26.

[7]Liang G C，Jiang L S.A modified structural model for credit risk [J].IMA Journal of Management Mathematics，2012，23（2）：147-170.

[8]Liu J，Tao M，Ma C，et al.Utility indifference pricing of convertible bonds [J].International Journal of Information Technology and Decision Making，2014，13（2）：429-444.

[9]Henderson V，Liang G.A multidimensional exponential utility indifference pricing model with applications to counterparty risk [J].SIAM Journal on Control and Optimization，2016，54（2）：690-717.

[10]Benedetti G，Campi L.Utility indifference valuation for non-smooth payoffs with an application to power derivatives [J].Applied Mathematics and Optimization，2016，73（2）：349-389.

[11]Hodges S D，Neuberger A.Optimal replication of contingent claims under transaction costs [J].Review of Futures Markets，1989，8（2）：222-239.