考虑混凝土受拉塑性应变割线刚度法的实现★
2018-05-14杨书琰
杨书琰 张 川
(1.重庆大学土木工程学院,重庆 400045; 2.重庆大学山地城镇建设与新技术教育部重点实验室,重庆 400045)
0 引言
使用广泛的钢筋混凝土结构在地震等复杂受力状态下具有明显的非线性特征,这促使众多研究者寻找合适的方法和模型来刻画这一特征。其中比较有影响的是Vecchio.F.J在1986年提出的MCFT[1]。此后,Vecchio.F.J团队又基于割线刚度法和MCFT提出了一种钢筋混凝土非线性有限元算法,即不考虑混凝土受拉塑性应变的割线刚度有限元方法(后文中称为Vecchio.F.J方法)[2,3],并利用基于该算法的有限元程序Vector2对钢筋混凝土梁、柱、剪切板、剪力墙进行了大量的单调及滞回分析,取得了较大的进展。可是在其提出的方法中,钢筋考虑了受拉、受压塑性应变,而混凝土仅考虑了受压塑性应变。在2003年,该团队Palermo.D博士曾提出考虑混凝土受拉塑性应变的割线刚度法(后文中称为Palermo.D方法)[4],但是该应变的引入给程序带来数值问题,最终Palermo.D方法未能实现。
由于Vecchio.F.J方法中不考虑这一应变,在分析混凝土起控制作用的滞回加载构件,如剪切板、低矮剪力墙时,该方法能够较为准确预测构件的极限承载力,但是分析得到的力—位移曲线(包括应力—应变曲线)往往显得干瘪,表现出强烈的捏缩效应,对构件耗能性能的模拟严重失真。为了解决这一问题,有必要在Vecchio.F.J方法中引入混凝土受拉塑性应变,而这一做法实现的最大困难在于解决该应变引入带来的数值问题。
1 改进型割线刚度法的提出
为了实现这一目的,首先需要通过算例的分析找到该数值问题产生的特点。选取处于纯剪力低周往复作用的SE8板[5]为对象,该板的材料属性及其他重要参数如表1所示。在Palermo.D方法中,各阶段中塑性应变取为应力应变曲线与应变轴的交点值,而某一点的割线刚度取为该点应力应变与塑性应变点连线的斜率。经过大量试算发现,Palermo.D方法中出现的数值问题具有阶段性,数值问题往往发生在混凝土某一主方向的应变ε<0且该方向的应变增量Δε<0的阶段。在这一阶段,混凝土在这一主方向上的割线刚度只能维持在1×102MPa或者1×103MPa的数量级,而在另一个主方向上割线刚度维持1×102MPa的数量级,如图1所示,而这一阶段对应于图1中的第30到第35荷载步。需要注意的是,如果单元第1,i荷载步的混凝土主拉方向角分别为θ1,θ2,那么满足∣θi-θ1∣≤45°的方向称为受拉立先行方向,满足∣θi-θ1∣>45°的方向称为受压先行方向。

表1 SE系列板的材料属性和主要变量

作为对比,Vecchio.F.J方法分析得到结果则呈现出一定的规律性。从图1中可以知道,在该方法中,混凝土两个主方向的割线刚度总是一个处于1×104MPa的数量级,另一个处于1×102MPa的数量级,没有出现两个主方向上割线刚度均小于1×104MPa数量级的情况。当一个方向主方向割线刚度大幅减小时,另一方向的割线刚度能够快速地增大,补充前一个方向上的刚度损失。利用Vecchio.F.J方法中暗含的这一规律对Palermo.D方法中出现数值问题的阶段中塑性应变和割线刚度的计算方法进行改进,得到当前提出的改进型考虑混凝土受拉塑性应变割线刚度方法(后文中称为改进型方法)。为了说明的需要,混凝土滞回本构模型如图2a)所示,与Palermo.D方法相比,改进型方法主要在以下两方面进行了修改:
1)对于塑性应变,除图2a)中满足Δε<0且ε<0的过程以外,混凝土本构曲线上某一点按照Palermo.D型方法的要求计算塑性应变,而该阶段上的某一点对应的塑性应变取为0或者取为该点应变对应的受压塑性应变。
2)对于割线刚度,除图2a)中满足Δε<0且ε<0的过程以外,混凝土本构曲线上某一点按照Palermo.D型方法的要求计算割线刚度,而该阶段上某一点对原点或者该点应变对应的受压塑性应变值计算割线刚度。
2 材料滞回本构中应变路径的控制方法
此外,为了使改进型方法成为一种有效的分析方法,还需要提升该方法的收敛性。具体地,需要对程序中混凝土本构的应变路径控制方法进行改进。一般地,混凝土滞回本构选择应变增量Δε作为应变路径的控制参数。但是该应变路径控制参数依然会因为迭代计算时Δε正负符号的震荡为程序带来收敛问题。为了解决该问题,滞回中混凝土应变路径的控制采取“分阶段应变路径控制”方法,该方法的具体要求如下:
1)当单元处在正向再加载(包括加载)和负向卸载时,受拉先行区的应力应变路径取图2a)中应变增加的路径,受压先行区的应力应变路径取图2中的应变减少的路径。
2)当单元处在正向卸载和负向再加载(包括加载)时,受拉先行区的应力应变路径取图2a)中应变减少的路径,受压先行区的应力应变路径取图2中的应变增加的路径。
需要补充的是,在钢筋滞回本构中,应变路径的控制选取某一点应变相较于图2b)中应变反向点(εr,σr)的应变增量Δεr作为控制参数。具体地,当Δεr>0时,应力应变的计算发生在应变增加的路径;当Δεr<0时,应力应变的计算发生在应变减少的路径。结合有限元方面的其他知识,使用程序语言把上述方法代码化就得到了最终分析程序。接下来将利用算例验证该改进型方法的收敛性、有效性。

3 算例分析及模型验证
为了模型验证的需要,使用理论分析较为困难的滞回剪切板SE系列板[5]作为分析对象。自该实验完成以来,其一直被视为混凝土剪切性能模拟方法正确性验证的重要标尺。该系列板包括尺寸一致的3块板,分别为SE8,SE9,SE10板,该系列板的长×宽×高为1 524 mm×1 524 mm×285 mm,板中钢筋正交布置,其材料属性及加载时各方向的应力比例如表1所示。其中,SE8板、SE9板为纯剪力作用下的低周往复加载,SE10板为双轴受压和剪力共同作用下的低周往复加载。
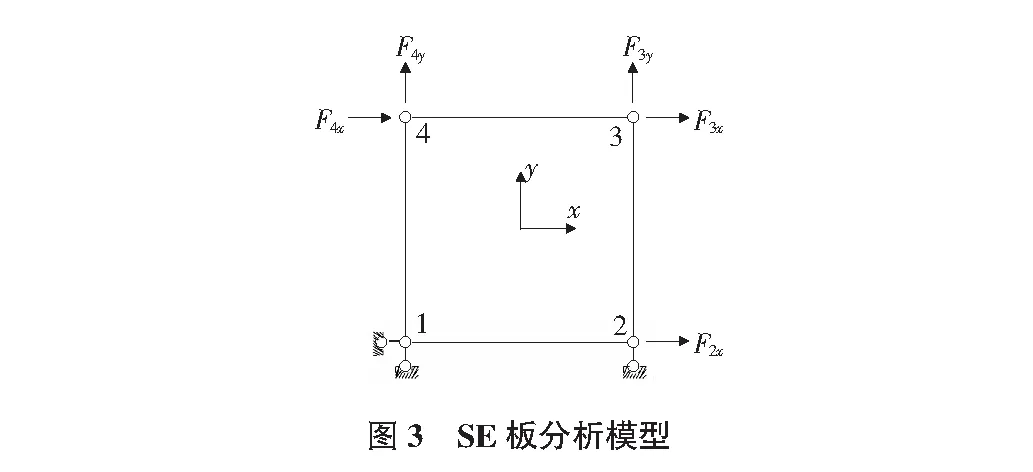
在分析时,分析模型选为1个矩形单元,如图3所示。其中,节点1的x,y方向,节点2的x方向被支座约束,板中加载应力的模拟通过图3中的节点力进行等效。同时,对比分析中的对象为Vecchio.F.J方法和改进型方法,在图3中前者使用“MCFT-1”代表,后者使用“MCFT-2”代表。
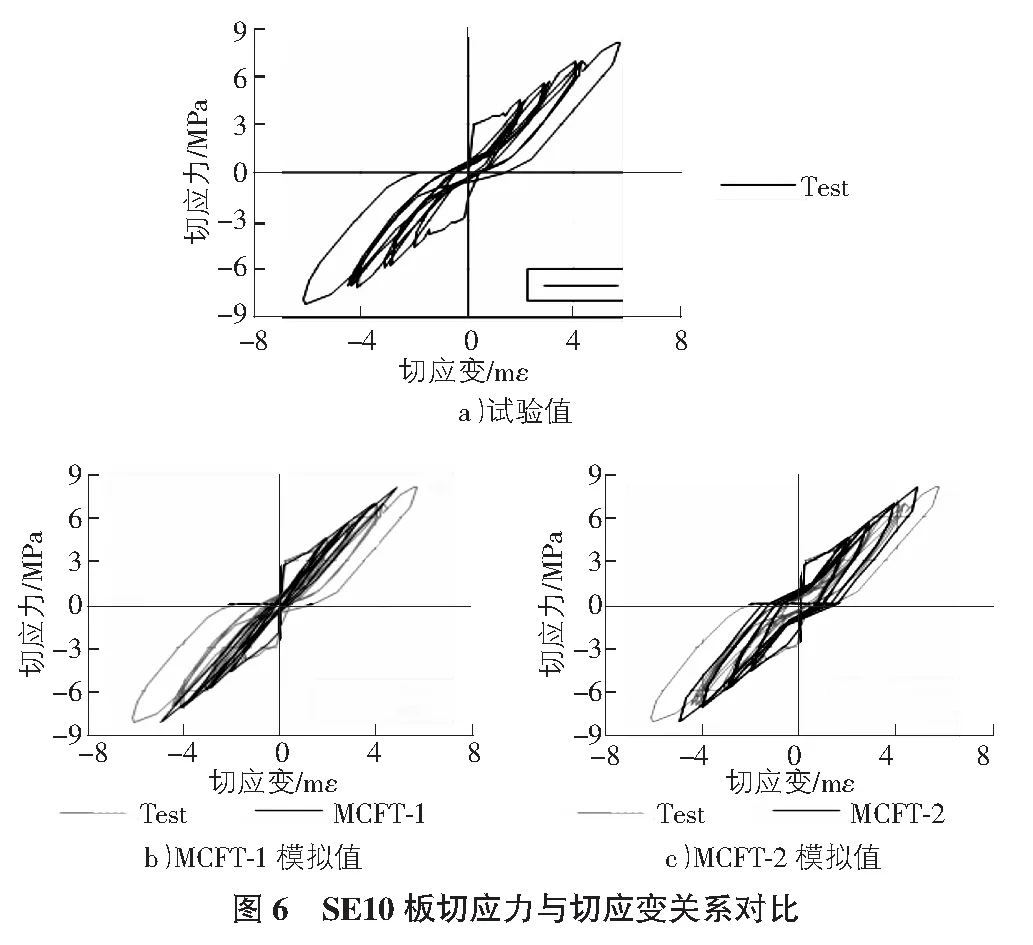
在材料模型的选择方面,两种方法中的钢筋模型相同,采用图2b)所示的Menegotto-Pinto模型,而混凝土模型的选择有所区别。在改进型方法中,混凝土采用考虑受拉、受压塑性应变的简化野口博模型,如图2a)所示。其中,受拉骨架线采用考虑混凝土受拉硬化的Vecchio1982模型,受压骨架线采用“峰值前Hognestad抛物线、峰值后Mander模型”的组合形式,受压混凝土考虑受拉软化效应,应力软化系数由Vecchio1982模型确定;滞回模型的加卸载模式选为线性加卸载规则。而两个模型唯一的区别是,在Vecchio.F.J方法中应力应变曲线在卸载时必须回到原点,即图2a)中H,H′的需要与原点重合。最终,SE8板、SE9板、SE10板的切应力与切应变关系模拟结果分别如图4~图6所示。


从模拟结果中可以看出,基于MCFT理论的Vecchio.F.J方法和改进型方法对SE板各圈切应力最大值处的切应变值的模拟是接近的,而这两型方法最大的区别在于分析曲线的饱满程度。对比Vecchio.F.J模型结果和试验可以知道,该方法预测的单元切应力与切应变曲线不饱满,这预示着该方法得到的滞回耗能性能与试验相差较大。而与前一种方法相比,改进型方法对SE板的切应力与切应变关系的模拟结果则大幅改善,曲线的饱满程度和对捏缩性能的模拟均与试验更加接近。
4 结语
通过以上算例的对比分析,可以得到以下3点结论:
1)考虑混凝土受拉塑性应变能够有效地改善Vecchio.F.J方法对往复荷载作用下剪切板的捏缩形态的预测结果,使得对变形的预测与试验更加接近。
2)改进型考虑混凝土受拉塑性应变割线刚度法是一种收敛的、可行的计算方法。
3)混凝土滞回模型程序化过程中使用的“分阶段应变路径控制”方法能够有效地提升程序的收敛性。
参考文献:
[1] Vecchio. F.J,Collins MP.The Modified Compression-Field Theory for Reinforced Concrete Elements Subjected to Shear[J].Journal of the American Concrete Institute,1986,83(2):219-31.
[2] Vecchio. F.J.Reinforced Concrete Membrane Element Formulations[J].Journal of Structural Engineering,1990,116(3):730-750.
[3] Vecchio.F.J.Towards cyclic load modeling of reinforced concrete[J].Aci Structural Journal,1999,96(2):193-202.
[4] Palermo D.Behaviour and Analysis of Reinforced Concrete Walls Subjected to Reversed Cyclic Loading[D].PhD Thesis.Graduate Depertment of Civil Engineering University of Toronto,2002.
[5] Stevens NJ,Uzumeri SM,Collins MP.Reinforced Concrete Subjected to Reversed Cyclic Shear-Experiments and Constitutive model[J].Aci Structural Journal,1991,88(2):46-135.
[6] 包洪余.基于全量割线刚度的钢筋混凝土二维非线性有限元分析[D].重庆:重庆大学硕士学位论文,2012.
[7] Ayoub A,Filippou FC.Nonlinear finite-element analysis of RC shear panels and walls[J].Journal of Structural Engineering-Asce,1998,124(3):298-308.
