基于带遗忘因子交替广义最小二乘法的多变量耦合系统参数辨识

焦慧方，陈希亮，高 敏，马忠玲

（1.西北大学 a.科学史高等研究院，b.继续教育学院，陕西 西安 710127；2.西安交通大学电气工程学院，陕西 西安 710049；3.西北工业集团，陕西 西安 710043）

近年来，随着工业自动化控制理论的不断发展，控制对象的复杂性也不断提高，有着多变量、强耦合等特征[1]。大多数情况下，被控对象数学模型往往是难以获得并且是时变的，为了实现最优控制，我们需要不断修正系统模型参数[2]。

系统辨识是一个通过观察系统输入、输出数据，来建立动态系统数学模型的方法。与理论分析法不同的是，系统辨识不需要深入了解系统的原理，只需要通过设计合理的实验来获得大量的实验数据，进行辨识计算，从而拟合出系统的数学模型。最小二乘法作为最基本的辨识算法，有着广泛的应用，但是最小二乘法每次处理数据量过大，需要消耗大量计算机资源易导致程序失去响应甚至死机[3-4]。递推最小二乘法是在最小二乘法基础上进行优化，不仅可以减小计算量和存储量，而且能实现在线实时系统辨识，但是估计结果往往是有偏的[5-6]。广义最小二乘法做了一些推广，能够实现无偏估计，但计算也变得很复杂[7-8]。

本文结合递推最小二乘法与广义最小二乘法的优点，加入遗忘因子，提出一种交替的广义最小二乘法，并通过dSPACE公司DS1103搭建了一个两入两出的水箱耦合系统，以验证该方法的有效性和可靠性。

在最小二乘法中，满足残差平方和最小的参数被认为是最佳估计值，其值为

1.2递推最小二乘法

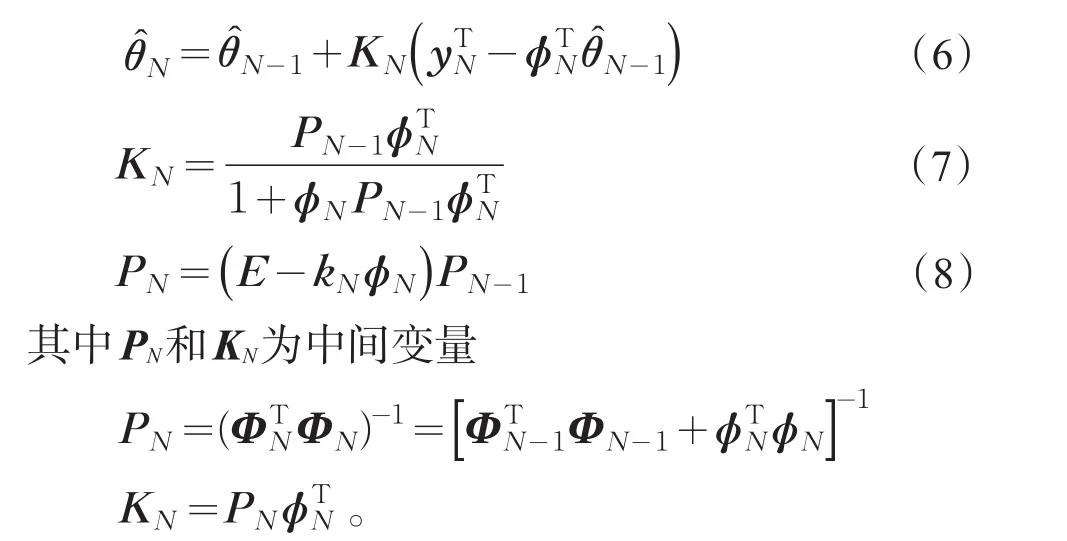
递推最小二乘法利用矩阵变化和矩阵求逆引定理，得到第N组估计值和第N+1组估计值的递推关系，

1.3广义最小二乘法

1传统最小二乘法

1.1最小二乘法

设线性定常系统的差分方程为

广义最小二乘法是针对线性自回归滑动平均模型（CARMA模型）的一种辨识方法，它能克服最小二乘法有偏估计。这种方法计算比较复杂，但效果比较好。设系统差分方程为其中u(k)和x(k)分别为系统输入信号和系统输出真实值，设x(k)的观测值为y(k)。

测得n+N个输出输入值y(1)，y(2)，… ，y(n+N)，u(1)，u(2)，… ，u(n+N)，可以得到N个方程，这N个方程的矩阵形式为

在广义最小二乘法中，有色噪声被替换为白噪声ε(k)通过线性系统后所得到的结果，目的是将有色噪声表示成白噪声，其向量矩阵形式

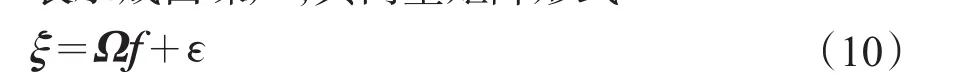
根据最小二乘法得到参数向量f的表达式为

设e(k)为 y(k)与式(3)的某一行 ŷ(k)之差，称 e(k)为残差，残差矩阵记为e，则

因为式(12)中ξ(k)是未知的，所以不能直接计算，只好在计算时用残差e(k)来代替ξ(k)，将代入系统方程得到白噪声ε(k)和系统参数的关系式。在此基础上由最小二乘法进行迭代计算得到 a1，a2，…，an，b0，b1，…，bn的无偏估计。

2带遗忘因子交替广义最小二乘法

通过对递推最小二乘法与广义最小二乘法进行优化，本文推导出一种交替广义最小二乘法。和最小二乘法相比，该方法辨识结果没有偏差。由式(2)与式(10)有

交替广义最小二乘法将方程组表示为

利用最小二乘法得到β的估计值

递推算法为

在式(18)中

其中

一般的递推算法适用于常参数估计，如果遇到时变参数，由于一般递推算法会受到大量老旧数据的影响，会降低新数据对辨识结果的影响，从而无法准确辨识出时变参数。我们可以引入遗忘因子来对新老数据加以权重影响，老数据的权重比较低，从而降低老数据对时变参数的影响，新数据的权重比较高，所以新数据对时变参数影响会加强。这样我们就可以较为精确地辨识出时变参数。

建立加入遗忘因子的系统辨识目标函数

式中0＜α≤1称为遗忘因子，也可称为加权因子。当α=1时，即为普通的递推最小二乘。对于0＜α＜1，时间越早的数据权重就越小，调整遗忘因子α的大小就可以调整遗忘数据的速度，α越小，遗忘旧数据的速度就越快。加入遗忘因子的交替广义最小二乘辨识算法为

3实验分析

3.1实验装置

本文选用两入两出水箱系统来进行相应实验，该系统有着典型的非线性、大惯性、时变性、多变量、耦合性等特性。在工业控制中，有许多被控对象均可抽象成水箱液位控制系统的数学模型，中水箱通过阀门向下水箱排水，下水箱通过阀门向储水箱排水，两个水泵分别供水。两个输入分别为电动调节阀开度、变频器输出，两个输出分别为中、下水箱水位，输入输出之间存在耦合关系，实验对象模型如图1所示。

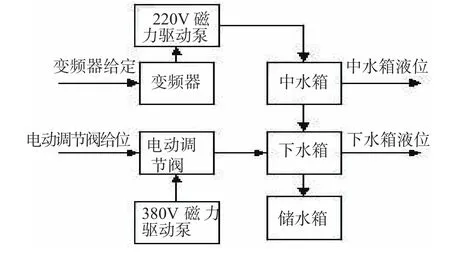
图1实验对象模型

3.2实验对象模型

由图1，设通过220V磁力驱动泵进入中水箱的流量记为u1(t)，通过阀门排出中水箱的流量记为x1(t)，中水箱液位高度记为y1(t)，中水箱截面积记为A1，通过电动调节阀进入下水箱的流量记为u2(t)，通过阀门流出下水箱的流量记为x2(t)，下水箱液位高度记为y2(t)，下水箱截面积记为A2。根据水总量不变，即入流量减去出流量等于液位高度变化率乘水箱截面积，可得到。

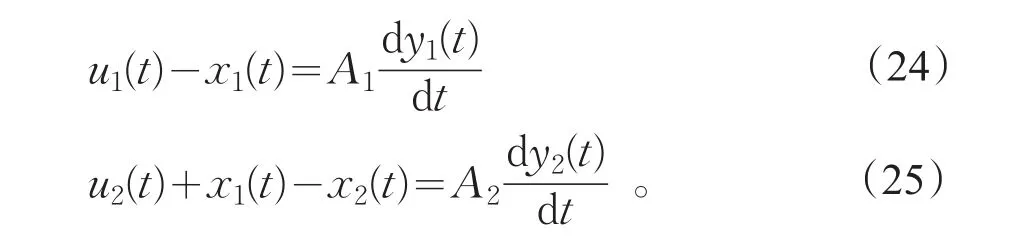
当液位平衡的时候，出水量等于入水量，即液位变化率为0，则有

当出水量不等于入水量时，液位会发生变化，进而出水口压力变化，导致出水量也发生变化。由流体力学知识可得，流体在紊流的情况下，液位高度与流量之间成非线性关系。为简化模型，可作如下近似处理：认为液位高度与流量呈线性关系，流量与液位高度成正比，与阀门阻力成反比。设中水箱出水阀阻力记为R1，下水箱出水阀阻力记为R2，则可得

将式(26)、(27)代入式(24)、(25)中，再进行拉氏变换可得

由式(28)与式(29)可得实验系统数学模型

由式(30)，图1所示的两入两出水箱系统是一个多回路之间相互耦合的多输入多输出系统。

3.3实验结果

3.3.1启动阶段

系统在启动阶段先采用手动运行，待系统辨识结果稳定后再切入自动运行。实验中系统启动阶段的输入信号、输出信号、辨识结果如图2所示。由图2(a)可以看出，手动阶段输入信号是一个阶跃信号和随机信号的叠加，这样的输入信号可让辨识算法对系统进行充分辨识。在50 s左右，系统切入自动模式。从图3(c)可以看出，切入自动模式时系统辨识结果基本稳定，此时切入自动模式是在一个较为准确的数学模型基础上的。

3.3.2中水箱设定值改变

切入自动控制后，液位可由算法自动控制。图3(a)、(b)、(c)分别为中水箱设定值由1.6 V降到1.4 V之后系统的输入信号、输出信号、辨识结果。而下水箱设定值保持1.2 V不变。

由图3(a)可得，设定值变化后中水箱液位迅速下降，而下水箱液位先有一定上升，然后下降，随后平稳到原先的1.2 V设定值，而中水箱也经过一段调整，稳定在1.4 V设定值上。理论上中水箱液位变化不会影响到下水箱，但是因为辨识模型和真实对象有一定误差，有一定波动，之后在控制算法作用下趋于稳定。

图2 启动阶段实验结果

从图3(c)中可以看出，系统辨识结果开始有一定波动，随后在30 s时候回归稳定。系统进入正常算法控制阶段，之所以有波动是因为电动调节阀的控制信号在20 s左右降为0，信号的0输入会对系统辨识造成一定影响，所以在30 s前液位变化波动很大，辨识算法会进行一段时间的辨识，到30 s时辨识结果稳定，控制算法会使液位逐渐趋于设定值。

图3中水箱设定值改变

4结论

本文针对多变量耦合系统，在传统最小二乘法基础上，提出了一种带遗忘因子交替广义最小二乘法，该方法结合了递推最小二乘法与广义最小二乘法的优点，既能够实现无偏估计，计算又得到简化。该方法应用于多变量耦合系统，通过在线系统辨识，能够快速跟踪系统时变参数，可以获得高精度参数估计。最后通过dSPACE公司DS1103搭建了一个两入两出的水箱耦合系统，实验结果表明该系统辨识方法的有效性和可靠性。

参考文献：

[1]王东风，李利平，王丽君.球磨机制粉系统控制的现状和前景[J].东北电力技术，2002（5）：5-9.

[2]毛丁辉，邱建琪，史涔溦.基于转动惯量的异步电机参数自整定系统研究[J].机电工程，2015，32（6）：830-835.

[3]刘静纨.最小二乘法在系统辨识中的应用[J].北京建筑工程学院学报，2004（3）：19-22.

[4]熊小伏，陈康，郑伟，等.基于最小二乘法的光伏逆变器模型辨识[J].电力系统保护与控制，2012，40（22）：52-57.

[5]赵海森，杜中兰，刘晓芳，等.基于递推最小二乘法与模型参考自适应法的鼠笼式异步电机转子电阻在线辨识方法[J].中国电机工程学报，2014，34（30）：5386-5394.

[6]荀倩，王培良，李祖欣，等.基于递推最小二乘法的永磁伺服系统参数辨识[J].电工技术学报，2016，31（17）：161-169.

[7]仇振安，何汉辉.基于广义最小二乘法的系统模型辨识及应用[J].计算机仿真，2007（10）：89-91.

[8]史贤俊，廖剑，马长李，等.基于MATLAB的广义最小二乘参数辨识与仿真[J].计算机与数字工程，2009，37（8）：173-175.