基于结构方程模型的多层调节效应*
2018-05-14温忠麟
方 杰 温忠麟 吴 艳
(1广东财经大学人文与传播学院,广州 510320)
(2华南师范大学心理学院/心理应用研究中心,广州 510631)
(3广东外语外贸大学应用心理学系,广州 510420)
1 前言
在心理、教育和管理等社科研究中,经常遇到多层(嵌套)数据的调节效应,称为多层调节(multilevel moderation)效应。例如,团队认同在教师人格与教师职业倦怠关系中起调节作用(王昊,周奕欣,王可欣,周明洁,2015),数据是教师嵌套于学校的两层结构,只有团队认同是在学校层面的测量,属于 2×(1→1)调节(这三个数字依次代表调节变量、自变量和因变量的层次,数字 2表示层次2,数字1表示层次1,以下类同)。又如,组织文化强度在组织创新文化与个体创新行为之间起调节作用(陈卫旗,2013),数据是员工嵌套于公司的两层结构,只有个体创新行为是在个体层面的测量,属于2×(2→1)调节。再如,领导−成员交换在任务绩效风险考量与管理者授权行为之间起调节作用(杨英,龙立荣,周立芳,2010),数据是员工嵌套于公司的两层结构,只有任务绩效风险考量是在公司层面的测量,属于 1×(2→1)调节。还有,与同事人际关系在员工工作满意度与平行建言之间起调节作用(段锦云,施嘉逸,凌斌,2017),所有变量都是在员工个体层面测量,属于1×(1→1)调节。
研究者常用多层线性模型(multilevel model,MLM)进行多层调节效应分析(方杰,邱皓政,张敏强,方路,2013),但多层线性模型将所有变量都设定为显变量并假设所有变量的测量不存在测量误差,因此难免会造成参数估计的偏差(方杰,邱皓政,张敏强,2011;方杰,温忠麟,张敏强,任皓,2014)。多层结构方程模型(Multilevel Structural Equation Model,MSEM)可以设置潜变量,有效控制误差,是比较好的方法。本文讨论如何利用MSEM 进行多层调节效应分析。以较为常用的2×(1→1)调节效应为例,在介绍多层线性模型的调节效应建模方法后,讨论了多层结构方程模型如何进行调节效应分析;接着,总结出一套多层调节SEM分析流程;然后,用一个例子说明如何用Mplus程序进行多层调节SEM分析;随后评述了多层调节效应分析方法在国内心理学的应用现状,最后对相关问题进行了讨论和拓展。
2 基于多层线性模型的调节效应分析
其实,2×(1→1)多层调节效应模型就是一般的多层线性模型,包含下面方程:
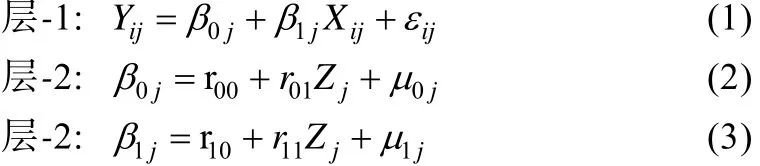
以员工嵌套于公司为例,方程中的下标i表示员工,j表示公司。将方程(2)、(3)带入方程(1)得:
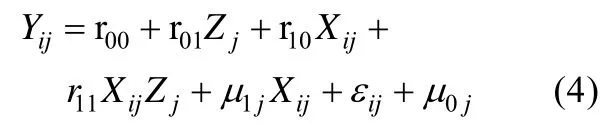
2×(1→1)多层调节效应又被称为跨层调节效应(cross-level interaction),调节项为 XijZj(见方程(4)),跨层调节效应的大小由回归系数 r11表示,如果回归系数 r11显著不为 0,则表示跨层调节效应显著。
上述多层调节分析方法(见方程(1)~(4))容易解释且操作简单,方便应用。但这种方法有不足之处,从方程(4)可以看出,主效应 r10没能区分Xij的组内和组间效应,调节效应 r11没能区分跨层调节和层2调节效应(Ender &Tofighi,2007;方杰,张敏强,邱皓政,2010)。解决的方法是,将层1自变量按组均值中心化后进行建模,同时将组均值及其与 Zj的交互项置于层2(廖卉,庄瑗嘉,2012):
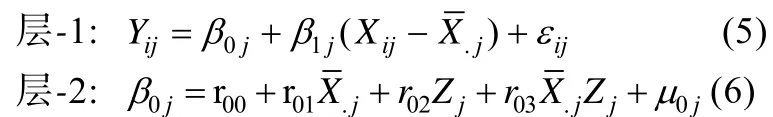
将方程(6)、(3)带入方程(5)得:
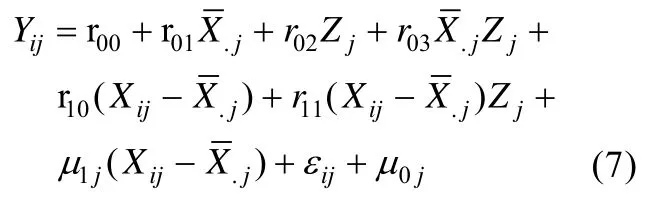
此时,系数 r10只表示自变量的组内差异的效应,系数 r01表示自变量的组间部分X.j的效应,从而区分了变量的组内和组间效应。的系数 r11表示跨层调节效应,的系数 r03表示层2调节效应。这就控制了层2调节作用,从而得到真实的跨层调节效应估计值 r11。
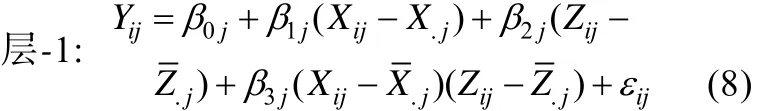
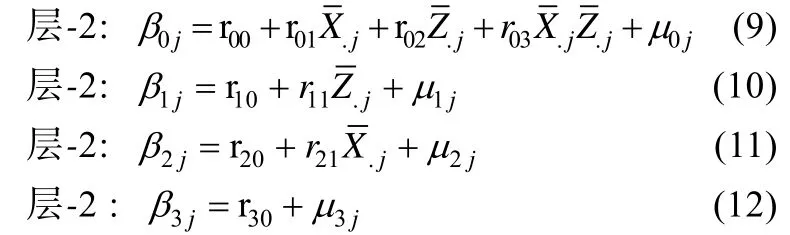
下面是一个更复杂的 1×(1→1)多层调节效应模型:将方程(9)至(12)代入方程(8)可知,的系数 r30表示层1调节效应,的系数 r03表示层 2调节效应,的系数r11表示跨层调节效应,的系数 r21表示另一个跨层调节效应(Preacher,Zhang,&Zyphur,2016)。
3 基于多层结构方程模型的调节分析
如果数据来自J个公司的 I个员工,其中,J个公司是从公司总体中随机抽样,员工是从样本公司全体员工中随机抽样,作为从层 1整合出来的层2变量,相比其他自然的层2变量(如Zj)更难控制抽样误差。因为从层 2的公司总体中抽取公司后,层 2变量(如 Zj)就确定了,所以只需要增加层2的样本量就可以控制Zj的抽样误差;但从层2的公司总体中抽取公司后,层2变量还不确定,因为不仅受层 2抽样的影响,同时还受层1抽样的影响。要想有效控制的抽样误差,需要同时增加层1和层2的样本量,这无疑增大了研究成本和难度。有学者提出将看成是无法直接观测的潜变量,使用多层结构方程模型(MSEM)进行分析,能较好控制的抽样误差(Lüdtke et al.,2008;Lüdtke,Marsh,Robitzsch,&Trautwein,2011;方杰等,2011,2014)。
已有研究者指出,多层结构方程模型(MSEM)会自动地将所有层1测量的变量(如 Xij)分解为组内部分和组间部分,组间部分用潜变量 Uxj表示,组内部分用Rxij表示,则跨层调节项为 RxijZj,层 2调节项为UxjZj(方杰等,2014;Preacher et al.,2016)。Ryu(2015)指出,正是由于 Uxj和 Rxij是潜变量,因此多层结构方程模型无法按照一般调节效应的分析步骤,先要计算出潜调节项 UxjZj和 RxijZj(包括潜调节项的乘积指标),然后再分析调节效应。
有两种无需计算潜调节项的多层调节 SEM分析方法(Preacher et al.,2016),这两种方法都无需产生乘积指标,都能在 Mplus软件上方便实现(见附录)。第一种方法是随机系数预测(Random Coefficient Prediction,RCP)法,即将随机斜率β1j当成因变量,做随机斜率1jβ对调节变量jZ的回归(见方程(3)),如果回归系数11r显著,就表示跨层调节效应显著(见方程(7))。第二种方法是潜调节结构方程(Latent Moderated Structural equations,LMS)法。LMS方法直接分析指标的分布,将全部指标的分布近似为一个有限的混合分布,每个分布都是条件正态分布,其分布函数的对数用 EM算法(Expectation Maximization algorithm)进行多层调节效应估计(Klein &Moosbrugger,2000;温忠麟,刘红云,侯杰泰,2012;温忠麟,吴艳,侯杰泰,2013)。
Preacher等(2016)对RCP和LMS法在多层调节效应分析中的作用进行了模拟比较。结果表明,在跨层调节效应分析中(对应于),RCP和LMS法的表现相当,但在层2调节效应分析中(对应于),RCP相比LMS法会产生更大的参数估计偏差并存在更多的不收敛情况。另外,LMS法适用于任何多层调节效应分析,但RCP法无法适用于1×(1→1)调节模型的层1调节效应的分析(见方程(8))。因此,在跨层调节效应分析中,建议使用RCP法,因为 RCP与LMS法效果相当,并且多数人比较熟悉这种方法;在同层调节效应分析中,建议使用LMS法。
值得注意的是,Mplus软件使用LMS法进行多层调节分析时,未提供常用的 RMSEA、CFI、TLI等拟合指数值。那如何判断基于LMS的多层调节SEM模型可以接受呢?判断方法有两种,第一种是利用对数−似然比检验(log-likelihood ratio test),根据 Mplus结果中的0H 值,计算−2LL值(不含潜调节项的基准 SEM 模型和包含潜调节项的多层调节SEM模型的似然比之差),−2LL值近似服从χ2分布,χ2分布的自由度为基准SEM模型和多层调节 SEM 模型的自由度之差,如果−2LL值的卡方检验结果显著,就表示多层调节模型更好(Klein &Moosbrugger,2000;Maslowsky,Jager,&Hemken,2015)。第二种是利用AIC判断,如果AIC变小,就表示多层调节模型更好,因为 AIC越大表示信息损失越多(Sardeshmukh &Vandenberg,2017)。
面对一个多层调节效应的SEM分析任务,研究者应当如何进行呢?根据前面的讨论,我们总结出一套多层调节效应的SEM分析流程(见图1)如下:
(1) 建立多层调节模型。模型的建立应该基于学科理论、文献资料和过往经验,模型中的每个路径关系都应当有依据,有关变量之间先后顺序的确定可参见温忠麟(2017)。
(2) 是否将层 1变量的组均值放入层 2作为自变量。如果是,则进入步骤3;如果不是,则使用多层线性模型(MLM)进行调节分析。
(3) 使用多层结构方程模型(MSEM)进行调节效应分析。如果是跨层调节效应,则选用 RCP法进行分析;如果是同层调节效应,则选用 LMS法进行分析。
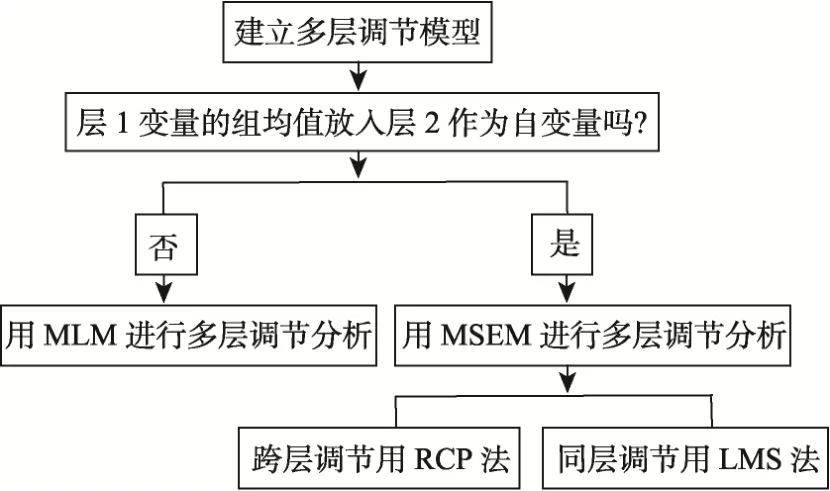
图1 多层调节分析流程
4 示例
接下来用一个示例演示如何用图1的流程检验多层调节效应。本例的数据(100个组,每组10人)由模拟产生,采用Mplus 7.4软件进行分析(多层调节分析的Mplus程序见附录)。
步骤一,假设本例要研究的是领导−部属交换关系差异化对仁慈领导与内部人身份感知关系的调节作用,使用 2×(1→1)多层调节模型(见方程(5)、(6)和(3)),领导−部属交换关系差异化是层2调节变量,仁慈领导是层1自变量,内部人身份感知是层1因变量。数据的零模型检验得到内部人身份感知的组内相关系数ICC (1) = 0.51 > 0.06,因此有必要进行多层分析。
步骤二,由于层 1自变量仁慈领导的组均值放入层 2作为预测变量,因此选择使用多层结构方程模型(MSEM)进行调节效应分析。
步骤三,用多层结构方程模型(MSEM)进行调节效应分析时,既有跨层调节效应,选用 RCP法进行分析;又有层2调节效应,选用LMS法进行分析(见方程(7)),因此本例需将RCP和LMS法混合使用。多层结构方程模型的结果如下:
首先,判断包含LMS的多层调节SEM模型的拟合情况。结果显示,包含潜调节项的多层调节SEM模型的Log Likelihood = −2862.37,AIC =5758.737,相比基准 SEM模型的 Log Likelihood值(−2948.97),增大了86.6,即−2LL 值为 86.6,自由度增加1,−2LL值的卡方检验显著(p < 0.001);相比基准 SEM 模型的 AIC值(5929.94),减少了170.5,都表明多层调节SEM模型相比基准SEM模型更好。
其次,多层调节效应的检验结果显示,跨层调节效应显著(11r = 0.139,SE = 0.089,p < 0.001),即当关系差异化水平越高,仁慈领导与内部人身份感知之间的正向关系越强;层 2调节效应不显著(03r = 0.158,SE = 0.09,p = 0.08)。为更加清晰地揭示关系差异化水平在仁慈领导和内部人身份感知关系中的跨层调节作用,随后进行简单斜率检验(Preacher,Curran,&Bauer,2006)。结果显示(图 2),在高领导−部属交换关系差异化的情境下(平均数加一个标准差),仁慈领导与内部人身份感知的正向关联性较强(简单斜率为 0.27,p <0.01);比较一下,在低领导−部属交换关系差异化的情境下(平均数减一个标准差),仁慈领导与内部人身份感知的作用不显著(简单斜率为−0.05,p > 0.05)。
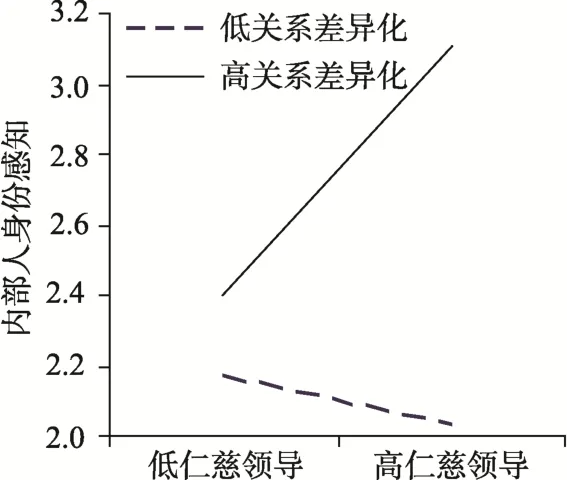
图2 调节效应的简单斜率图
5 应用现状分析
多层调节分析方法在国内心理学的应用现状如何?以中国期刊网全文数据库为数据源进行搜索,从2010年1月1日到2017年7月31日,国内 10本心理学期刊中,共找到 29篇多层调节的应用研究。以下仅对这29例应用研究进行述评。
第一,从发表杂志来看,《心理学报》发表多层调节研究最多,共发表 12篇(41%),然后依次是《心理科学》6篇(21%),《中国临床心理学杂志》4 篇(14%),《心理发展与教育》3 篇(10%),《心理与行为研究》2篇(7%),《中国心理卫生杂志》和《应用心理学》各有1篇。
第二,从研究领域上看,国内心理学的多层调节研究主要集中在企业和学校。具体而言,14篇(48%)文章的研究对象都是企业员工,其中 10篇发表在《心理学报》上;14篇(48%)文章的研究对象是在校师生(大学生4篇、高中生5篇、小学生2篇,初中生、学前儿童和教师各1篇);1篇文章的研究对象为证券投资人。
第三,从研究内容上看,国内心理学的多层调节与多层中介模型相互整合的趋势明显。有10篇(35%)文章同时进行了多层调节和多层中介分析,其中 4篇明确提出并检验了有调节的多层中介模型。
第四,国内心理学的多层调节分析目前都只研究两层调节效应,且大都使用多层线性模型进行调节效应分析,只有 1篇(3%)用多层结构方程模型对 2-1-1多层中介的后半路径进行调节效应分析(段锦云等,2017)。
第五,从多层调节模型的类型上看,2×(1→1)调节模型使用的最多,共有19个研究(61%),6个研究(19%)使用2×(2→1)调节模型,1×(2→1)和1×(1→1)调节模型各有 3个研究,所有模型都将因变量设定在层1。
第六,就中心化而言,只有 8篇(28%)文章对层1自变量按组均值中心化,1篇文章对层1自变量按总均值中心化,3篇文章对层1自变量进行了均值中心化,但没说清楚是按总均值还是组均值的中心化,17篇(59%)文章没有对层1自变量的中心化情况进行报告。更进一步,只有杨付和张丽华(2012)的研究对层 1自变量按组均值中心化的同时,还将组均值置于层2,即只有1篇文章(3%)区分了层1自变量的组内和组间效应。更严重的问题是,没有文章进行多层调节效应的分解。
除了 2×(2→1)调节模型可直接使用多层线性模型进行分析外,其他多层调节模型应当区分层 1自变量的组内和组间效应,同时对多层调节效应进行有效分解,并使用多层结构方程模型进行调节效应分析,以得到更准确的调节效应估计值。
6 讨论与拓展
多层调节分析方法的发展过程是一个追求更准确的调节效应估计值的过程。综上所述,多层调节分析方法经历了三个发展阶段。第一阶段是将层1自变量按组均值中心化(见方程5),并将组均值作为层2自变量进入方程6,实现了层1自变量组间和组内效应的有效分离,改变了过去将组间和组内效应混为一团的情况。第二阶段是实现了多层调节效应的分解,改变了过去不加区分的情况。例如,2×(1→1)多层调节效应分解为跨层调节效应和层2调节效应两部分(见方程7)。第三阶段是是将组均值设置为潜变量,利用多层结构方程模型进行调节分析,有效控制抽样误差。我们总结出一套多层调节效应分析的SEM流程,并通过一个例子演示了如何进行多层调节效应的SEM分析。但是,本文仍然存在一些不足,尚需进一步深入讨论和拓展。
6.1 多层结构方程模型的拓展
第一,本文只讨论了多层结构方程模型控制抽样误差的问题。实际上,如果变量只有单一指标或者仅以量表总分作为唯一指标,还存在测量误差(measurement error),即单指标导致变量的测验信度低,使得调节效应估计存在偏差。控制测量误差的方法就是对变量采用多指标测量(Mplus程序见附录)(Lüdtke et al.,2011;方杰等,2011,2014)。值得注意的是,随着模型复杂性的增加,模型的稳定性在降低,不收敛的风险在增大。因此,研究者在使用多层结构方程时,要注意权衡误差和稳健性的关系。Li和Beretvas (2013)的模拟研究表明,多层结构方程模型为了控制测量误差而使用多指标,这大大增加了参数估计的数目,也就意味着需要用更大的层 2样本量才能避免模型不收敛的情况出现。Lüdtke等(2011)的 2个模拟研究也一致表明,当层2信息少(ICC和层2样本小)时,控制部分误差的分析方法相比同时控制抽样误差和测量误差的分析方法会有更准确的参数估计。Lüdtke等(2011)接着用一个实例表明,校正抽样误差比较校正测量误差更有意义。
第二,本文只涉及了多层结构方程对因变量在层 1的多层调节效应分析。实际上,多层结构方程还能对因变量在层 2的多层调节(例如 1×(1→2)、1×(2→2)和 2×(1→2)调节)进行分析,相比多层线性模型(只能分析因变量在层1的多层调节效应)具有更广的适用性(Preacher et al.,2016;方杰等,2014)。值得注意的是,此时只有层2调节效应存在(Preacher et al.,2016)
多层结构方程虽然有诸多优点,但也存在计算耗时较多和数据收敛困难的问题(Depaoli &Clifton,2015;Preacher et al.,2016)。可行的解决方法有以下三种。第一,如果研究模型既包括跨层调节,又包括同层调节,则可尝试将RCP和LMS法混合使用,以减少运行时间(Preacher et al.,2016)。本文示例中,如果仅用 LMS法(程序见附录)将多耗费 21.7%的时间。第二,将多层线性模型的调节效应分析结果当成多层结构方程的调节效应分析的初始值(start values)(Depaoli &Clifton,2015;Preacher et al.,2016)。第三,可用贝叶斯法进行多层调节效应分析。在多层结构方程模型中使用贝叶斯法,也无需产生乘积指标,同样能在Mplus软件上方便实现(温忠麟等,2012)。已有模拟研究比较了贝叶斯法和极大似然(Maximum Likelihood,ML)方法在多层结构方程中的表现,结果发现,贝叶斯法能有效改善数据收敛困难或不合理收敛(如负方差)的问题,贝叶斯方法还能在某些(如样本量和 ICC都小)情况下,改善层 2估计的准确性(Depaoli &Clifton,2015;Zitzmann,Lüdtke,Robitzsch,&Marsh,2016)。值得注意的是,目前Mplus软件只能将贝叶斯法和RCP法整合在一起进行多层调节效应的SEM分析,还未能实现贝叶斯法和LMS法的整合。
6.2 多层调节模型的拓展
第一,本文仅将组均值及其与 Zj的交互项置于层2的截距方程(见方程(6)),本研究的分析方法还能拓展到同时将组均值及其与的交互项置于层 2的斜率方程(见方程(13)),将方程(6)和(13)代入方程(5)可知,2×(1→1)多层调节模型又增加了跨层调节效应和(程序见附录)。
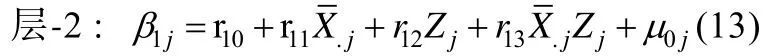
第二,本文所涉及的多层调节都设定为只有一个调节变量的两层调节效应。实际上,本研究的分析方法还能拓展到多个调节变量的高阶调节效应分析,Preacher等(2016)实现了两个层2调节变量、层1和层2各一个调节变量的三阶调节效应分析。另外,已有研究已经实现了三层中介效应的多层结构方程分析(方杰等,2014),本研究的分析方法也能拓展到三层调节模型,当前 Mplus软件允许在多层结构方程框架下,使用RCP法和贝叶斯法进行三层调节效应分析。
第三,本文只涉及了调节变量的多层结构方程模型研究。但是,许多实际问题可能同时包含调节变量和中介变量,将调节和中介变量整合起来进行研究已经成为一种趋势。Ryu (2015)将基于多层结构方程的调节模型研究拓展到 1-1-1有调节的中介模型研究,包括 1-1-1中介的后半路径分别被层1调节变量调节或层2调节变量调节的有调节的中介模型,但 Ryu (2015)只研究了同层调节效应,既不考虑跨层调节效应,又不涉及LMS方法,也没研究其他有调节的中介模型和有中介的调节模型,因此基于多层结构方程模型的中介和调节混合研究还有待深入。
从统计层面上讲,基于多层结构方程模型的多层调节分析还处于发展和完善阶段,除了讨论中已经提到的问题外,还存在诸多值得探讨的课题,例如,已有模拟研究发现,多层结构方程模型得到准确的参数估计值是以统计功效降低(即第Ⅱ类错误率增加)、需要大样本为代价的(方杰等,2014),如何提高多层调节分析的统计功效呢?在确保参数估计的准确和足够统计功效(0.8)的前提下,各层所需最小的样本量是多少?Hayes和Montoya (2017)提出了基于多元线性回归的多类别自变量(至少三个类别)的调节效应分析方法,那么基于多层结构方程模型的多类别自变量的调节效应如何分析呢?方法的进步给研究者提供了一个深入理解和应用多层结构方程模型进行调节分析的机会,相信随着多层结构方程模型和多层调节效应研究的深入,会不断增加我们对多层调节效应和多层结构方程问题的理解。
参考文献
陈卫旗.(2013).组织创新文化、组织文化强度与个体员工创新行为: 多层线性模型的分析.心理科学,36(5),1187–1193.
段锦云,施嘉逸,凌斌.(2017).高承诺组织与员工建言:双过程模型检验.心理学报,49(4),539–553.
方杰,邱皓政,张敏强.(2011).基于多层结构方程模型的情境效应分析: 兼与多层线性模型比较.心理科学进展,19(2),284–292.
方杰,邱皓政,张敏强,方路.(2013).我国近十年来心理学研究中 HLM 方法的应用述评.心理科学,36(5),1194–1200.
方杰,温忠麟,张敏强,任皓.(2014).基于结构方程模型的多层中介效应分析.心理科学进展,22(3),530–539.
方杰,张敏强,邱皓政.(2010).基于阶层线性理论的多层级中介效应.心理科学进展,18(8),1329–1338.
廖卉,庄瑗嘉.(2012).多层次理论模型的建立及研究方法.见 陈晓萍,徐淑英,樊景立 (编),组织与管理研究的实证方法 (第2版,pp.553–587).北京: 北京大学出版社.
王昊,周奕欣,王可欣,周明洁.(2015).团队认同对教师人格与职业倦怠关系的跨层调节作用.中国临床心理学杂志,23(4),741–745.
温忠麟.(2017).实证研究中的因果推理与分析.心理科学,40(1),200–208.
温忠麟,刘红云,侯杰泰.(2012).调节效应和中介效应分析.北京: 教育科学出版社.
温忠麟,吴艳,侯杰泰.(2013).潜变量交互效应结构方程:分布分析方法.心理学探新,33(5),409–414.
杨付,张丽华.(2012).团队沟通、工作不安全氛围对创新行为的影响: 创造力自我效能感的调节作用.心理学报,44(10),1383–1401.
杨英,龙立荣,周丽芳.(2010).授权风险考量与授权行为:领导-成员交换和集权度的作用.心理学报,42(8),875–885.
Depaoli,S.,&Clifton,J.P.(2015).A Bayesian approach to multilevel structural equation modeling with continuous and dichotomous outcomes.Structural Equation Modeling:A Multidisciplinary Journal,22(3),327–351.
Enders,C.K.,&Tofighi,D.(2007).Centering predictor variables in cross-sectional multilevel models: A new look at an old issue.Psychological Methods,12(2),121–138.Hayes,A.F.,&Montoya,A.K.(2017).A tutorial on testing,visualizing,and probing an interaction involving a multicategorical variable in linear regression analysis.Communication Methods and Measures,11(1),1–30.
Klein,A.G.,&Moosbrugger,H.(2000).Maximum likelihood estimation of latent interaction effects with the LMS method.Psychometrika,65(4),457–474.
Li,X.,&Beretvas,S.N.(2013).Sample size limits for estimating upper level mediation models using multilevel SEM.Structural Equation Modeling: A Multidisciplinary Journal,20(2),241–264.
Lüdtke,O.,Marsh,H.W.,Robitzsch,A.,&Trautwein,U.(2011).A 2×2 taxonomy of multilevel latent contextual models: Accuracy-bias trade-offs in full and partial error correction models.Psychological Methods,16(4),444–467.
Lüdtke,O.,Marsh,H.W.,Robitzsch,A.,Trautwein,U.,Asparouhov,T.,&Muthén,B.(2008).The multilevel latent covariate model: A new,more reliable approach to group-level effects in contextual studies.Psychological Methods,13(3),203–229.
Maslowsky,J.,Jager,J.,&Hemken,D.(2015).Estimating and interpreting latent variable interactions: A tutorial for applying the latent moderated structural equation.International Journal of Behavioral Development,39(1),87–96.
Preacher,K.J.,Curran,P.J.,&Bauer,D.J.(2006).Computational tools for probing interactions in multiple linear regression,multilevel modeling,and latent curve analysis.Journal of Educational and Behavioral Statistics,31(4),437–448.
Preacher,K.J.,Zhang,Z.,&Zyphur,M.J.(2016).Multilevel structural equation models for assessing moderation within and across levels of analysis.Psychological Methods,21(2),189–205.
Ryu,E.(2015).The role of centering for interaction of level 1 variables in multilevel structural equation models.Structural Equation Modeling: A Multidisciplinary Journal,22(4),617–630.
Sardeshmukh,S.R.,&Vandenberg,R.J.(2017).Integrating moderation and mediation: A structural equation modeling approach.Organizational Research Methods,20(4),721–745.
Zitzmann,S.,Lüdtke,O.,Robitzsch,A.,&Marsh,H.W.(2016).A Bayesian approach for estimating multilevel latent contextual models.Structural Equation Modeling: A Multidisciplinary Journal,23(5),661–679.
