基于最小二乘拟合的科学级CMOS传感器非均匀性校正
2018-05-11闫苏琪杨世洪王明富洪裕珍
闫苏琪 ,杨世洪 ,王明富 ,洪裕珍
(1.中国科学院光电技术研究所四川成都610209;2.中国科学院大学北京100049)
科学级互补金属氧化物半导体(scientific Complementary Metal Oxide Semiconductor,sCMOS)相比于传统光电传感器具有灵敏度高、线性度好以及分辨率高等突出优点,而被广泛应用到各个领域[1]。由于不同列的列放大器内部晶体管阈值电压和自身偏置电压不同会产生固定模式噪声,其图像中表现为竖直条纹。sCMOS芯片元信号的顶部和底部分别采用独立的输出,输出后信号被双列放大(低增益通道、高增益通道),并分别进行A/D转换[2],因此对于高、低增益通道需要分别进行非均匀性校正。本文以低增益通道为例进行校正,其工作饱和度范围(0,95%]。
鉴于CMOS图像传感器的响应特性以及工程上要在硬件上实现且对实时性的要求,因此适宜选用计算量小、存储参数小的校正方式[3]。其中基于两点标定的两点法最大的缺点是应用的动态范围小[4]。而基于最小二乘法两点法以及二阶多项式拟合法充分利用多个辐照度下的数据,使校正算法可适应的动态范围更大,但仍可能存在在某辐照范围内校正效果比较差,甚至校正后图像的均匀性变差的情况。因此提出通过基于最小二乘的分段线性校正算法,使在整个工作辐照度下都有较好的校正效果。
1 针对光电响应线性度良好模型的非均匀性校正
1.1 校正原理
非均匀校正技术是改善图像非均匀性的有效方法。非均匀性校正的目的就是通过校正使得图像传感器所有光敏单元在相同辐照度下表现出完全相同的光电转换关系。目前常用的非均匀校正方法主要有基于标定的校正方法和基于场景的校正方法[5],由于sCMOS稳定性比较好所以适用于基于标定的校正方法,而后者虽然具有无需参考源自适应校正的能力,但是其精确算法的硬件实现相当困难,因而工程实际应用中还是使用前者。
基于最小二乘法的曲线拟合,当选取的用于曲线拟合的定标点个数大于校正系数个数时,就导致在求取系数时存在非一致方程。非一致方程的最小二乘解有可能不是唯一的,但是不同的最小二乘解得到的Ax和Ax-y是唯一的[6]。非一致方程Ax=y的最小二乘解是非唯一的,存在通解形式为:

然而由于最小二乘解是只有在满足Moore-Penrose条件时,可以得到Moore-Penrose逆矩阵A+,由性质可以,广义逆矩阵A+是唯一的,所以可得到唯一最小二乘解。
1.2 两点校正法
两点法不仅对暗电流做了补偿还对增益做了校正,可以对线性度好的传感器有很好的校正效果[7]。假设光电传感器的光电响应是线性的,那么每个像元的响应可表示为:

式(2)中,x为像元所受辐照度,yij(x)为在辐照度为x的第i行、第j列像元的输出响应,本文用灰度值表示输出响应,lij为此像元的增益系数,mij为此像元的偏移量,每个像元有独立的的增益系数和偏移量且不随时间变化是固定的,因此校正公式可表示为:
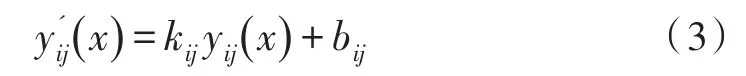
式(3)中,kij和bij分别为两点法的校正增益和校正偏移量。
基于两点定标的一般两点法是取两个辐照度x1、x2下的响应确定一条直线,并假设该直线与理想光响应曲线一致为绝对线性的[8]。得到单个像素单元的响应yij(x1)、yij(x2),所有像元的平均响应输出和。令,得到如式(3)的线性方程组,经解方程组得到每个像素单元独立的校正系数kij和bij,再代入式(2)即可对每个像元进行校正,可得:

由最小二乘原理出,最可信赖值应在使残余误差平方和为最小的条件下求得。因此,当标定点选取N=n,,即满足残差平方和最小的条件时,可得基于最小二乘的两点法校正系数[9]。要使条件满足,构建函数如下:


1.3 多项式拟合法
多项式拟合校正算法主要针对光响应线性度比较差,不适于线性拟合的情况[10]。相比于两点法和多点法,该方法需要进行更多的乘法运算消耗更多的硬件资源。
每个像元的响应可表示为:

式(7)表示像元的响应可以用n阶多项式来表示。
校正公式可表示为:
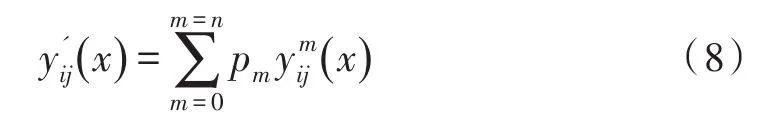
1.4 分段线性插值算法
两点校正法基于光电传感器的光电响应曲线是线性模型,具有算法简单、易于工程上实时实现,而随着非线性的程度加剧,两点法的校正误差变大[12]。为了在光电响应曲线呈非线性时更好的对其非均匀性进行校正,Milton等人提出多点法。多点法又称为分段线性插值算法。因为所有像元在不同曝光量区间均有不同的校正参数,就可以避免在整个曝光区间统一校正参数带来局部误差偏大的问题,所以校正精度较高[13]。分段区间选取的越多,校正效果越好,但在划分分段区间时并没有一标准的理论依据,造成分段区间的选取只能靠反复性实验获得,效率很低。
因此,本文提出基于最小二乘的分段线性校正算法,以各段拟合曲线的残差平方和最小为依据,即可得到最佳拟合效果,从而获得最佳分段点。针对如何确定拟合直线的条数,一种方法是根据具体的工程要求,人工的进行设定;另一种方法是给定一个阈值,当连续x个点拟合得到残差平方和小于这个阈值,而连续x+1个点拟合得到的残差平方和大于这个阈值,那么就可确定这连续的x个点作为一个分段区间,剩余点以同样方法划分分段区间[14]。因工程需要,用于存储校正参数的空间有限,本文以分两段为例,当满足下列条件时,得到两组校正系数kij1、bij1,kij2、bij2。满足N1+N2=N,
2 实验所用sCMOS图像传感器
本相机系统采用长光辰芯光电公司生产的GSENSE2020s型sCMOS图像传感器。该sCMOS光电传感器的分辨率为2048*2048、A/D转换位宽是12 bit,即其灰度值范围0~4 095,对于整个像素阵列的读取方式是分4个通道同时逐行进行读取,因此在进行非均匀性校正时需要考虑边界处有没有明显的灰度差别,是否需要在各通道连接处进行非均匀性校正。
评定经均匀性校正处理前后的图像的非均匀性指标:NU值大小、灰度直方图分布,采用NU值来表征图像传感器的非均匀性[15],其定义如下:

式(9)中,sd为输出图像信号的标准差,mu为均值。NU值的大小体现了图像传感器非均匀性的程度。
3 实验验证
3.1 光电响应实验
为了确定使用何种方式进行非均匀性校正,首先需要了解实验所用传感器的光电响应特性,因此使用积分球提供均匀光源进行性能测试,本实验在相同曝光条件下,不同辐照度下各抓取20帧图像并用20帧图像所有像素平均值绘制光电响应曲线。图像传感器光敏单元的光响应曲线反映了该光敏单元输出与辐照度之间的关系,是图像传感器的非均匀性的体现。经分析仿真得到传感器整体的光响应曲线,由于相机工作所处的工作模式决定在读取像元像素值时是分4个通道同时读出的,因此同时绘制了4个通道的光响应特性曲线,如图1所示。

图1 sCMOS传感器光电响应曲线
图1中所示横轴为传感器所受辐照度,对于整个传感器的曲线其纵轴表示整幅图像的平均灰度值,而各通道曲线所对应的纵轴表示各通道像元的平均灰度值。从图中可以显然得出以下几点结论:实验所用光电传感器的光响应线性度比较好;在平均灰度值小于2 000的范围内各通道的光响应特性几乎一致,当平均灰度值大于2 000时各通道的光响应特性略有差异。
3.2 使用最小二乘法拟合光响应曲线
从图1得到的光响应线性度很好的结论中,可以初步判断可采用两点法、分段线性插值或低阶多项式拟合的方法进行非均匀性校正。由于实验中所使用传感器低增益通道正常工作输出响应范围为饱和度0至95%,因此使用最小二乘法拟合这一范围的光电响应曲线。分别进行一阶线性拟合、分两段线性拟合和二阶多项式拟合,结果如表2所示。
表2中,根据残余误差平方和可以看出:使用两点法拟合度明显不如另外两种方式;使用分两段的线性拟合度与二阶多项式拟合度差距很小。因此,可知使用两点法进行非均匀校正效果将最差,而是用另外两种方式,校正效果将差别不大并且采用本文提出的算法校正效果很有可能优于二阶多项式拟合法。

表2 曲线拟合结果
3.3 校正效果比较分析
图2两幅图中,横轴均表示传感器所受辐照度,其单位为Lx,纵轴均表示图像非均匀度,单位%。分析两幅图可得到结论:经本文提出的基于最小二乘的多点法(分段线性插值算法)相比于两点标定的一般两点法在整个工作照度范围下校正效果有明显的提高;基于最小二乘的两点法和基于最小二乘的二阶多项式法拟合校正法在低照度下校正效果很差、甚至校正后的非均匀性变高,而本文提出的算法就可以改善这一问题,使适应性更强;因此所提出的优化算法有明显的优势。
图3为经本文提出的基于最小二乘的分段线性差值算法校正前后的对比图,左侧为未经校正的灰度图像,右侧为经校正后的。不经校正前的图像质量明显存在竖条纹以及一些人为疵点,而经校正后的图像从主观上就可看出均匀性相当好,因此针对非均匀性校正的研究仍然很有必要。所用器件低增益通道校正前的非均匀度为1.41%,表3为几种校正算法的校正算法汇总情况,可以看出本文提出的算法相比其他几种算法对平均非均匀性校正明显更有优势。

图2 校正前后非均匀度对比

图3 校正前后的图像

表3 几种校正算法在整个工作照度下的平均校正效果
4 结 论
本文从非均匀性产生的原因出发,利用积分球产生均匀光源测试了sCMOS的光电响应特性。根据光电响应特性曲线,筛选出几种适当的校正方法包括,基于两点标定的一般两点法、基于最小二乘的两点法基于最小二乘的二阶多项式拟合法进行校正分析。并总结了几种校正算法的原理以及优缺点,提出了基于最小二乘法的分段线性插值算法,使在整个工作照度下都可获得很好的非均匀校正效果。经试验验证其算法相比其他几种经典算法,可适应均匀性降低更大。同时计算量以及要存储的参数很少,适宜于工程实现[16],如FPGA实现。除此外,经过调整对比度,让看不出几个通道间有明显的非均匀性,因此没有对通道间非均匀性进行校正。
参考文献:
[1]吴胜.SCMOS高速成像系统关键技术研究[D].重庆:重庆大学,2015.
[2]孙宏海,何舒文,吴培,等.高动态科学级CMOS相机设计与成像分析[J].液晶与显示,2017,32(3):240-248.
[3]黄万伟.Xilinx FPGA应用进阶[M].北京:电子工业出版社,2014.
[4]刘则洵,全先荣,任建伟,等.CCD相机输出非均匀性线性校正系数的定标[J].红外与激光工程,2012,41(8):2211-2215.
[5]吕雷,张学峰.基于FPGA的红外图像实时非均匀性校正[J].激光与红外,2011,41(6):641-643.
[6]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2013.
[7]何火胜.红外图像两点非均匀性校正算法工程实现[J].科技与创新,2014(12):4-5.
[8]郭文豹,魏仲慧,何昕,等.CMOS图像传感器非均匀性实时校正算法研究[J].微电子学与计算机,2011,28(2):171-174.
[9]陈伟杰.最小二乘法原理及其在实验曲线拟合中的应用分析[J].辽宁科技学院学报,2014,16(4):33-34.
[10]程旺,吕群波,赵娜.基于FPGA的科学级CMOS图像传感器非均匀性校正[J].半导体光电,2016(6):873-875.
[11]黄英东,安建波.基于改进多项式拟合的红外焦平面非均匀性校正方法[J].红外,2011,32(3):29-33.
[12]夏玫,顾国华,陈钱,等.IRFPA两点校正的定标温度选择方法研究及实现[J].红外技术,2011,33(3):151-154.
[13]张红辉,罗海波,余新荣,等.多点标定的自适应非均匀性校正方法[J].红外与激光工程,2014,43(11):3651-3654.
[14]田垅,刘宗田.最小二乘法分段直线拟合[J].计算机科学,2012,39(b06):482-484.
[15]严奕,邓若汉,陈永平,等.有源像素CMOS图像传感器非均匀性研究[J].科学技术与工程,2011,11(15):3449-3455.
[16]梁超,马天翔.基于黑体标定的红外图像非均匀性校正系统设计[J].中国光学,2016,9(3):385-393.
