确定性均匀递归树的谱分析

刘远超，赵海兴，梁 静

（1.青海师范大学数学与统计学院，青海西宁810008；2.青海师范大学计算机学院，青海西宁810008）

均匀递归树（Uniform Recursive Tree，URT）是随机图中一种很重要的模型。随着URT模型在中世纪家族宗谱以及流行疾病传播等领域中的应用[1-3]，人们又提出了确定性均匀递归树（Deterministic Uniform Recursive Tree，DURT）的模型，对 DURT 的网络特性的研究已经有了很多的结果[4-9]。这些结果从多个方面展示了DURT的网络特性，例如度分布、平均路径长度、介数分布以及度相关性等。

对于DURT的谱的研究也同样有大量的结果[4-5，10]。其中在文献[4]中提出，DURT的拉普拉斯矩阵的特征值随生成过程呈现出迭代的关系。基于这个结果，我们提出了推广的拉普拉斯矩阵Lk=kD-A，通过对推广的拉普拉斯矩阵的特征值进行分析，我们发现DURT的拉普拉斯矩阵特征值的迭代关系也同样适用于邻接矩阵的特征值。同时对无符号拉普拉斯矩阵做同样的推广，对其特征值分析也发现了同样的迭代关系，并且对于相同的，推广的无符号拉普拉斯矩阵的特征值与推广的拉普拉斯矩阵的特征值是一致的，这些结果与二部图（树）的拉普拉斯矩阵的特征值与无符号拉普拉斯矩阵特征值是一致的结论是相吻合的。

文中通过构造推广的拉普拉斯矩阵，并对其特征值进行分析得到的这些结果，对我们进一步了解DURT生成过程中特征值的变化提供一些帮助。

1 DURT的生成模型

DURT是一个通过逐次迭代的过程产生的.我们用t表示网络的生成的步数，用Ut表示经过t步之后生成的DURT模型。于是DURT的生成过程为：当t=0时，U0是由两个顶点以及与之相连的一条边构成；当t≥1时，Ut通过在Ut-1的基础上的每一个顶点产生一条边以及与这条边相连的一个新顶点，前四步的生成过程如图1所示。

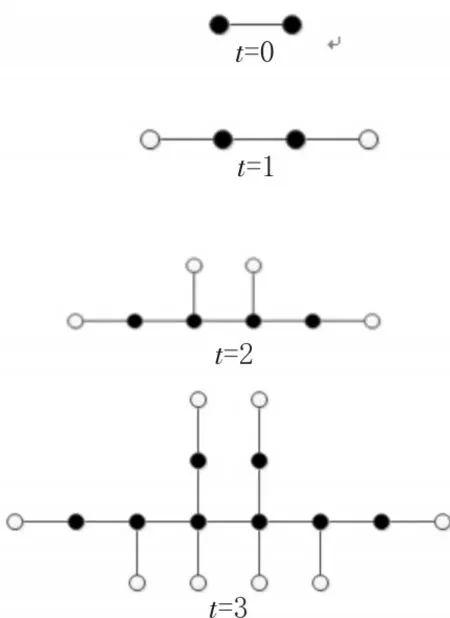
图1 DURT生成过程的前4步

图1中，每一步中的白色的顶点即为新生成的顶点。

用nt表示第t步中顶点的数目，用mt表示第t步中边的数目，那么显然有

因为这个网络是个树，于是

在这个网络中顶点的最大度是t+1，并且是第0步中就存在的那两个顶点。

2 推广的拉普拉斯矩阵

文中是基于文献[4]的基础上做的进一步的研究，文献[4]提出DURT的拉普拉斯矩阵的特征值随生成过程呈现出迭代关系。于是我们设想DURT的拉普拉斯矩阵为什么会存在递归关系，它的拉普拉斯矩阵有何特别之处。于是我们构造了推广的拉普拉斯矩阵Lk=kD-A，并对推广的拉普拉斯矩阵的特征值进行分析。

图的拉普拉斯矩阵和无符号拉普拉斯矩阵的谱的研究已经有了大量的结果[10-15]，本文未说明的符号和专用名词参考文献[16]。

我们用At表示DURT第t步的邻接矩阵，那么邻接矩阵满足下面的递归关系：

这里的每一个块都是2t×2t的矩阵，It-1是一个单位矩阵。

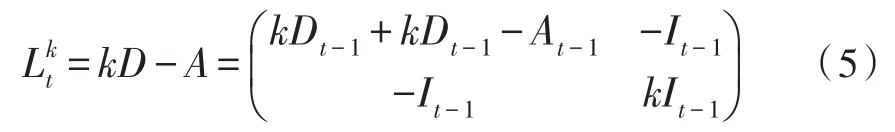
这里N1=(x-k)It-1-kDt-1+At-1，N2=f(x)It-1-kDt-1+At-1以及。

根据等式（6）我们可以得到：

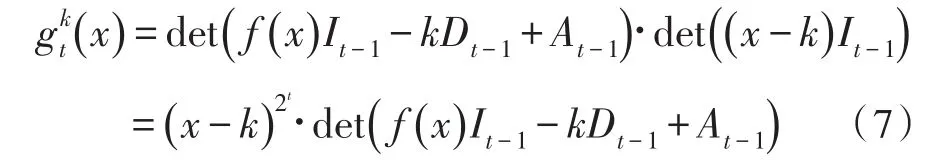
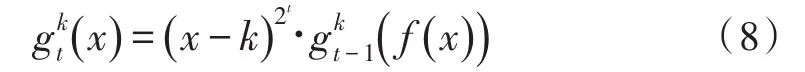
根据这个递归关系式，我们可以得到下面的递归关系式：

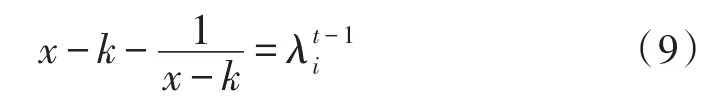
因此我们可以从式子（9）中由第t步的特征值推出第t+1步的特征值：

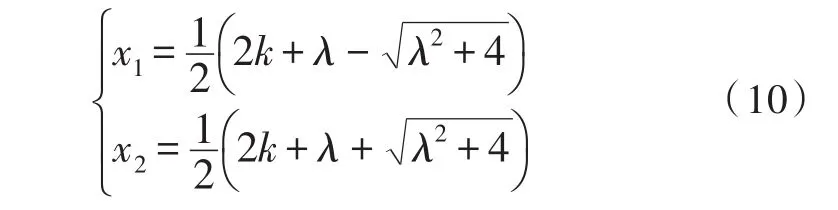
式子（10）是一个很重要的递推关系式，因为我们根据这个式子由每一步的特征值都可以直接推出下一步的特征值。

定理1：推广的拉普拉斯矩阵的第步的特征值为λ1=k-1和λ2=k+1。

证明：

所以第0步的特征值是λ1=k-1和λ2=k+1。

定理2：DURT的邻接矩阵也满足递归关系，并且特征值关于点对称。

证明：当k=0时，推广的拉普拉斯矩阵就是-A，由定理1，-A的两个特征值是±1，因此A的两个特征值也是±1。于是根据等式（10）我们可以得到第1步中的4个特征值

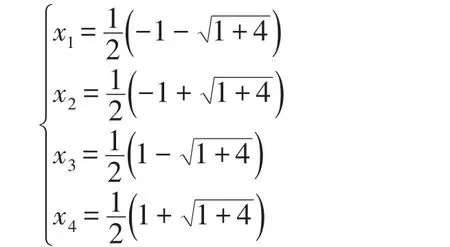
显然有x1=-x4，x2=-x3。从而我们可以根据式子（10）推出DURT的邻接矩阵的第t步的特征值有以下性质：

即邻接矩阵的特征值关于零点对称（如图2所示）。

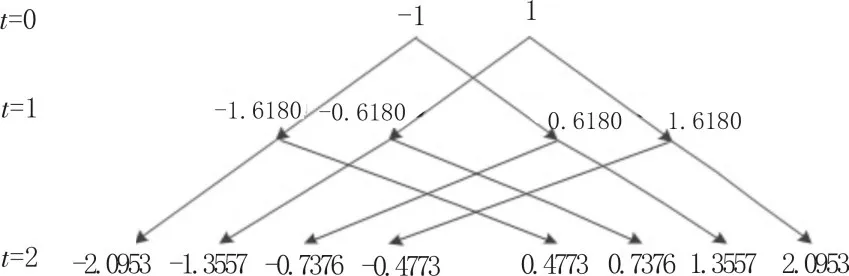
图2 当t=0,1,2时网络的邻接矩阵的特征值分布

当k=1时，即拉普拉斯矩阵。第0步的两个特征值由定理1可知是1和2。并且根据式子（10），我们把0和2代入之后发现0所迭代出的两个特征值是0和2，所以0和2是DURT生成过程中每一步的拉普拉斯矩阵的特征值。同时由于每一步中都有0和2，所以第t步中的特征值将全部出现在第t+1步中。

定理3∶0和2是DURT每一步的拉普拉斯矩阵的特征值，并且第t步中的特征值将全部出现在第t+1步中，且出现的位置是奇数位置（特征值按照递增排序）。

证明：由于第0步的特征值是0和2，并且0所迭代出的两个特征值是0和2，所以0和2是每一步中的特征值。

假定由第0步的特征值0在第t+1步所迭代出的所有特征值记为Tt+1，那么第1步中的特征值0在第t+1步中所迭代出的特征值就是Tt，所以第t步中的特征值将全部出现在第t+1步中，如图3所示。

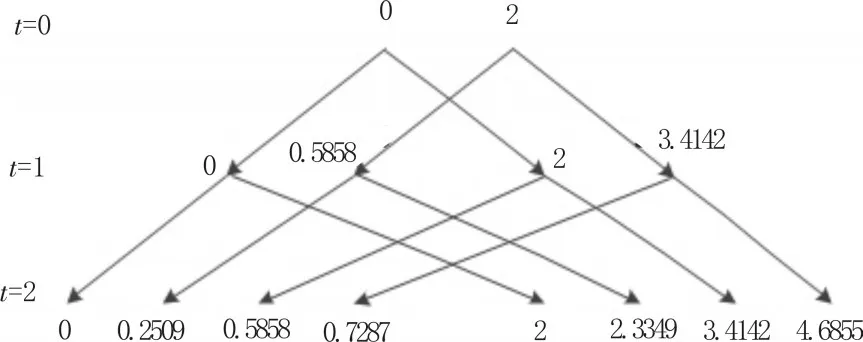
图3 当t=0,1,2时网络的拉普拉斯矩阵的特征值分布

对于它们出现的位置我们由数学归纳法证明：

根据式子（10），我们由数学归纳法：

当t=1时的4个特征值

假设当t=n-1时也成立，即第t=n-1步中的奇数位置的特征值与第t=n-2步中的特征值完全相同，所以在第t=n步中，由第t=n-1步中的奇数位置的特征值所迭代出的特征值与第t=n-1步中的特征值完全相同。根据式子（10），第t=n-1步中的每一个特征值所迭代出的两个特征值中一个严格小于1，另一个严格大于1。且由可知λ越大，x1的值也就越大，从而第t=n-1步中的2n个特征值所迭代出的第t=n步中的前2n个特征值的位置就是第t=n-1步中的2n个特征值的位置。同理，第t=n步中的后2n个特征值也是第t=n-1步中特征值的位置，所以当t=n时，定理是成立的。

当k=-1时，即负的无符号拉普拉斯矩阵，由定理1可知，此时的特征值为0和-2，我们利用式子（10）代入0和-2：

此时的结果与k-1时恰好是相反数的关系，且为负的无符号拉普拉斯矩阵的特征值，故无符号拉普拉斯矩阵的特征值与拉普拉斯矩阵的特征值是一致的，所以我们的推广满足二部图（树）的拉普拉斯矩阵与无符号拉普拉斯矩阵的特征值是一致的这一定理。

定理4：DURT的推广的拉普拉斯矩阵的特征值与推广的无符号拉普拉斯矩阵的特征值是一致的。

证明：由二部图（树是一种特殊的二部图）的拉普拉斯矩阵特征值与无符号拉普拉斯矩阵的特征值是一致的就很容易的联想到这一点了。因为当k取负值的时候就是负的推广的拉普拉斯矩阵，因此对于k取负值的时候的特征值进行分析，然后再取相反数就是推广的无符号拉普拉斯矩阵的特征值。所以由上面普通拉普拉斯矩阵的特征值和无符号拉普拉斯矩阵特征值的关系进行同样的分析即可得到这个结果。

3 结 论

基于DURT的拉普拉斯矩阵的特征值的迭代关系，我们通过构造推广的拉普拉斯矩阵（无符号拉普拉斯矩阵），并且通过同样的方法进行分析，我们发现DURT的邻接矩阵也存在同样的递归关系，这是本文的一个核心部分，同时根据推广的拉普拉斯矩阵的特征值分析，也验证了树（DURT本身就是一棵树）的拉普拉斯矩阵特征值与无符号拉普拉斯矩阵的特征值是一致的。

文中基于DURT的模型而构造了推广的拉普拉斯矩阵，在未来的研究中，我们期待利用推广的拉普拉斯矩阵这一工具，在更多的模型中挖掘出更多的网络性质以及代数性质。

参考文献：

[1]Börner K，Sanyal S，Vespignani A.Network science[J].Annual Review of Information Science&Technology，2007，41（1）:537-607.

[2]方锦清，汪小帆，郑志刚，等.电子物理学:一门崭新的交叉科学:网络科学[J].中国学术期刊文摘，2008（3）:3.

[3]方锦清，汪小帆，郑志刚，等.电子物理学:一门崭新的交叉科学:网络科学Ⅱ[J].中国学术期刊文摘，2008（7）:3.

[4]Zhang Z，Zhou S，Yi Q，et al.Topologies and Laplacian spectra ofa deterministic uniform recursive tree[J].The European Physical Journal B，2008，63（4）:507-513.

[5]Sun W，Xuan T，Qin S.Laplacian spectrum of a family of recursive trees and its applications in network coherence[J].Journal of Statistical Mechanics Theory&Experiment，2016，2016（6）:063205.

[6]赵虎，赵海兴.GDURT演化模型的拓扑性质[J].电子设计工程，2013（12）:177-180.

[7]张科.两种确定性小世界网络模型的研究[D].西宁：青海师范大学，2014.

[8]章忠志，周水庚，方锦清.复杂网络确定性模型研究的最新进展[J].复杂系统与复杂性科学，2008，5（4）:29-46.

[9]赵二岭.几类确定性网络模型的特性研究[D].西宁：青海师范大学，2013.

[10]赵虎，王丽萍.分层编号法计算GDURT模型的拉普拉斯谱[J].青海师范大学学报（自科版），2015，31（1）:15-20.

[11]吴翠芳.关于图的谱和拉普拉斯谱[D].大连：大连理工大学，2005.

[12]李发旭，卫良.复杂网络的拉普拉斯和无符号拉普拉斯特征谱分析[J].青海师范大学学报:自然科学版，2016（4）:20-26.

[13]冯瑶.关于无符号拉普拉斯谱的研究[D].长沙：湖南师范大学，2014.

[14]曾沁雪.图的无符号拉普拉斯谱的若干结果[D].上海：华东师范大学，2012.

[15]王冬冬.图的无符号拉普拉斯谱和距离谱的研究[D].上海：华东理工大学，2015.

[16]Bondy J A，Murty U S R.Graph Theory and Applications[J].1976.

[17]赵玉厚，杨喜岗，杨忠，等.热分析特征值对蠕墨铸铁蠕化率的影响[J].西安工业大学报，2015（8）:642-647.