河南省县级行政区划空间形态特征分析与优化

李 欣 王先文

(1. 河南财经政法大学 中原经济区“三化”协调发展河南省协同创新中心, 河南 郑州 450046; 2. 河南财经政法大学 资源与环境学院, 河南 郑州 450046)

行政区划是集行政和经济管理功能为一体的国家内部区域范围划分，其边界形状是长期自然和人文因素共同作用的结果。行政区划边界形态特征不但影响了行政区划的边界管理、人口流动，而且也直接和行政区划及其之间的交通通信、经济状态相关。因此研究行政区划边界的空间形态特征，对研究区域历史，优化区域结构，提高经济水平都具有重要的理论和实际意义。

目前，地理、规划、生态等学科都对区域空间形态特征展开相关研究。研究主要分为两个方向：一是行政区划改革的政策性研究，如王爱民[1]对行政区跨政区协调体系的研究，熊曦[2]对行政区经济发展的研究等；二是对行政区空间形态特征测度法的研究，如Lee等[3]提出的定量测量区域空间形态方法，Batty等[4]提出的区域空间结构分形分析方法，郭腾云[5]提出的区域空间紧凑度与效率分析方法等。随着城乡一体化、智慧城市等应用需求的不断提出，相关研究也在不断发展，如城市形态信息图谱[6]，扩展回波式空间形态模式[7]，空间破碎化和形态趋同化问题[8]等，同时空间分析、遥感、经济地理学模型、社会网络分析等技术和方法也被引入到行政区划的空间形态研究中[9-11]，以上研究成果有利于区域土地利用规律的总结，对科学调整和规划土地利用具有一定指导意义。但以上研究主要是针对城市尺度，而对于市县一级中等尺度的行政区划形态研究，以及形态特征对于交通、农业、文化、经济的影响研究较少，不足以针对社会发展需要为行政区划改革提供参考依据。

通过上述分析，拟采用定量空间形态特征分析方法，对河南省县级行政区划空间形态特征进行研究，分析由于形态特征而产生的限制区域协调发展的问题，为行政区划界线优化管理和区域空间开发提供决策依据。

1 行政区划形态特征分析方法

1.1 分形维数

空间形态特征分形是地理信息科学研究的一个重要问题[12-15]，其中分形维数是定量描述区域空间形态特征的重要指标，反映区域边界轮廓的曲折复杂程度[16]。分形维数数值越大，则其边界线越复杂，区域形状越不规则。

利用网格法计算河南省各县市的分形维数，步骤：①将一个正方形网格覆盖在研究对象上，网格完全覆盖该研究对象，此时网格数为1；②将覆盖研究对象的正方形网格边平分为2份，即可得到2×2个网格单元，此时进行叠置分析，与研究对象边界重合的格网数量为N(1/2)，与研究对象内部区域重合的网格数量记为M(1/2)；③依此规则对初始正方形不断细分，将正方形边长平均分为2n份时，再次进行叠置分析，与研究对象边界重合的格网数量为N(1/2n)，与研究对象内部区域重合的网格数量为M(1/2n)。④经过9次细分即可得到9对数据，将其绘制在双对数坐标系上，利用最小二乘法进行线性拟合，得到的回归直线斜率即为分形维数。计算分形维数流程如图1所示。

图1 网格法计算分形维数流程

在对网格进行细分时，细分次数最大值一般取9，即格网最多分为9级，因为大于9级时，回归系数的稳定性将受到一定影响，从而导致自相似性减弱[17]。根据分形理论，有下式成立[18]：

lnN(1/2n)=C+DlnM(1/2n)1/2.

(1)

式中：C为待定常数，D为分型维数。

1.2 放射状指数

地理学中经常使用粗糙测度方法[19]和图形周界测度方法来定量表达图形放射状指数。Boyce-Clark放射状指数方法[20]是一种能够反映图形一般形状特征的测度方法，该方法基本思路是将图形与标准圆做对比，从而得到一个相对指数，通过该指数即可定量描述图形的形状特征。其计算式为

(2)

式中：SBC为Boyce-Clark放射状指数，ri为图形优势点到图形轮廓边界距离，n为以优势点为中心的呈均匀角度分布的辐射半径数量。优势点可以根据应用需要灵活选择，可以是图形几何中心，也可以是具有实际地理意义的区域中心，如行政中心、商业中心等。

Boyce-Clark放射状指数的优点在于建立了优势点与区域边界的相关关系，定量表达了区域内部与边界的联系，因此通过放射状指数也可以更加真实的反映区域内部联系，具有更加突出的实践意义。

1.3 紧凑度

区域边界形态的紧凑度是反映该区域空间形态的一种重要概念[21-26]，它是衡量图形空间聚集性和完整性的重要指标。其计算式：

(3)

式中：A为平面多边形面积，P为多边形周长，C为多边形紧凑度。

此计算方法将圆作为紧凑度值为1的标准度量单位，其他任意形状图形紧凑度值都小于1，图形越不规则说明与圆形形状区别越大，其紧凑度值越小。这一指标的优点在于以整数1作为测度标准，综合了图形的周长和面积特征，有利于多个区域之间的形态特征比较。

2 河南省县级行政区划形态特征分析

2.1 分形维数特征分析

采用了9种尺度的网格在ARCGIS软件下对河南108个县和18个地级市辖区的行政区划边界进行了叠置运算，每个县市得到9对数据，经过计算可得所有河南省县级行政区划分维数据，通过整理，所有对应数据的相关指数都在0.93以上，表明在9种尺度中分维数据具备分形性质。如表1所示。

表1 河南省县级行政区划分形维数

从表1中可以得出，分形维数最小值为1.231 533，最大值为1.326 276，分形维数最大差异为0.094 743。总体来说河南省县级行政区划的分形维数值较小，说明行政区划边界形状复杂程度总体较低，区划边界受到规划控制，较为紧凑节约，也有利于管理机构行政效率的提高。利用自然间断点分类法将所有行政区划分维数值分类显示，如图2所示。

结合河南自然地貌进行分析，可以看出分维较小的县主要位于郑州、新乡、平顶山、周口，这是因为河南中部区域位于黄淮平原，地势平缓，在划分行政区时主要有历史政治和经济因素决定，而受地形因素影响较少。分维较大的县主要位于安阳、濮阳、焦作、洛阳、南阳和驻马店，这是因为安阳和濮阳主要位于河南、河北和山东交界处，边界形状受到相邻省份影响，相对较为复杂，而焦作、洛阳和南阳位于我国第二级和第三级地貌台阶的过渡地带，嵖岈山位于驻马店境内，地形较为复杂，在划分行政区划时会受到地形影响。另外，从行政管理和执行效率角度来看，行政区划边界分形维数越高，其边界形状就越复杂，行政区之间的相互影响就越大，从而影响交通组织和经济交流，不利于区域的协调发展。郑州、新乡、平顶山、周口边界形状受地形因素影响较小，分维值也较小，有利于行政效率的提高，而安阳、濮阳、洛阳、驻马店部分县的边界形状受地形因素影响较大，形状相对复杂，行政效率也会因此受到一定影响。从图2中可以看出河南省县级行政区划边界形状的分维值和地形特征具有一定的耦合性，其复杂程度也会对行政管理效率产生一定的影响。

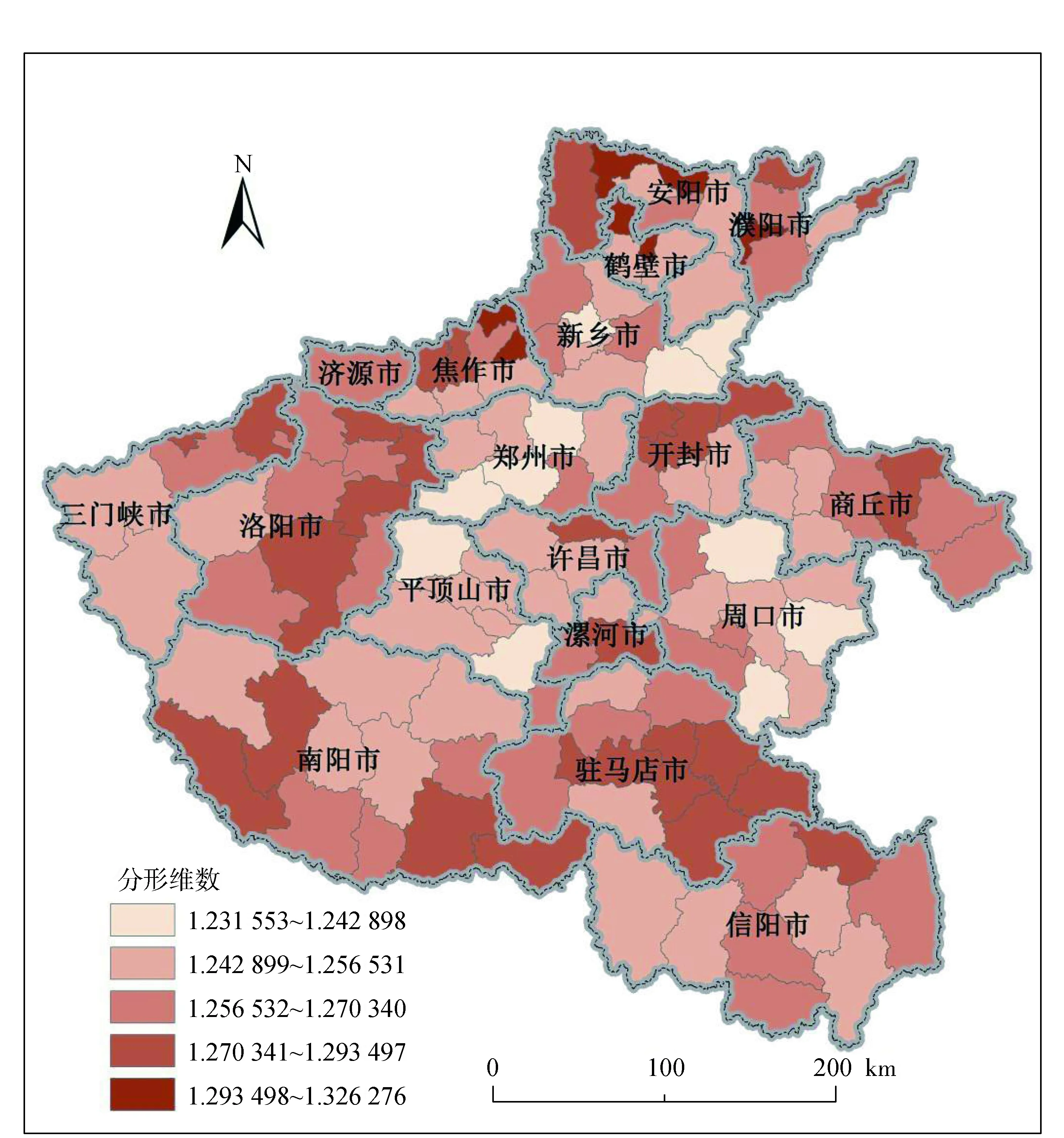
图2 河南省县级行政区划分形维数分类

2.2 放射状指数特征分析

使用了36条放射状射线计算县级行政区划的放射状指数，放射中心为县级行政区的优势点，本文使用了县政府所在位置作为区域优势点。利用式(2)，在地图中做叠加和裁剪运算，即可得到各县市的放射状指数。图3为河南省县级行政区划的放射状指数分类图。

使用的Boyce-Clark放射状指数方法体现了县级行政区划内优势点与边界之间的具体联系，图4和图5分别为河南省放射状指数最小和最大5个县级行政区划。

舞钢市、中牟县、邓州市、郑州市市辖区和太康县为放射状指数最小的5个县市，如图4所示，放射状指数为28～28.467 3，其政府所在位置接近行政区划的几何中心，有利于交通、通信及政府管理效率的提高，能够以较高效率推动区域发展。

而滑县、濮阳县、沈丘县、项城市和陕县为放射状指数最大的5个县，如图5所示，放射状指数为66.026 1～81.702 1，其政府位置位于行政区划边界，从图形和放射状指数中都可以看出该优势点相对于边界形状的结构较为松散，区域内其他位置相对于优势点的交通、通信成本较高，政府机构的管理和执行效率相对较低。

由于选用了县级政府所在位置为优势点，即图4和图5中的放射中心，体现了政府所在位置对其辖区的辐射带动作用。放射状指数越小，说明地理意义上的优势点例如行政中心、经济中心等，越接近图形几何中心，该优势点与区域内部的联系更加紧密；而放射状指数越大，表明相同面积情况下有更大的边界长度，行政区与外界有很大的接触面，优势点与其边界的联系则较松散，行政管理较为不便，不利于区域的协调发展。

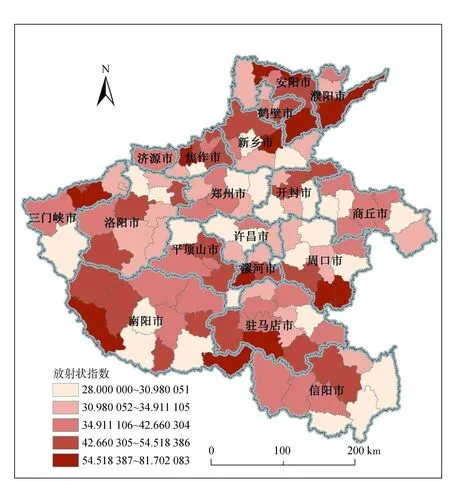
图3 河南省县级行政区划放射状指数分类

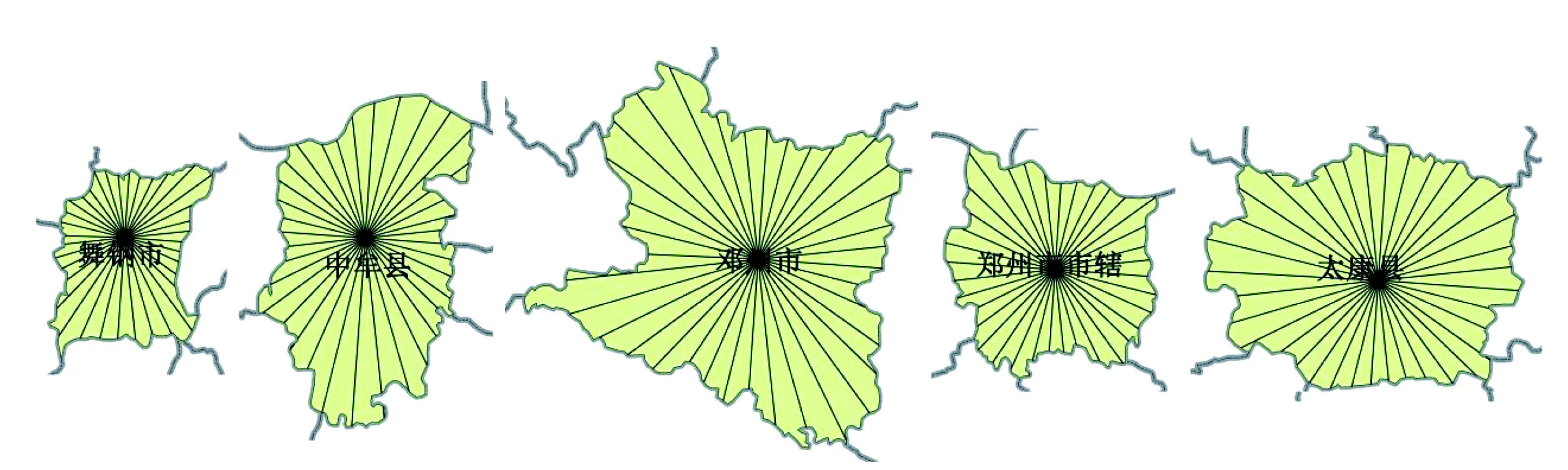
图4 河南省放射状指数最小的5个县级行政区划放射状

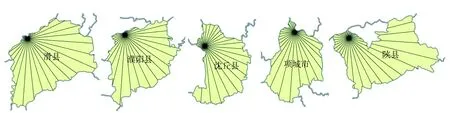
图5 河南省放射状指数最大的5个县级行政区划放射状

2.3 紧凑度特征分析

紧凑度是描述行政区划形状的重要测度指标，它在行政管理和区域规划等方面都是重要的参考指标。紧凑度取值范围为0～1，数值越小越松散，数值越大越紧凑。经过计算得到的各县市的紧凑度分类如图6所示。

图6 河南省县级行政区划紧凑度分类

从图6可以看出，安阳县、修武县、宝丰县、淅川县、汝南县和新乡县等县市的紧凑度较小，紧凑度值为0.384 873～0.536 142，而从图形形状上也可以明显看出，这些县市的形状与圆形形状相去甚远，此类行政区划形状会在一定程度上影响管理执行效率，从区域内部联系方面看，需要耗费更多成本才能满足管理需求，如“村村通”工程中，由于建设经费来源不同，且为了维护行政区划内部完整性，道路规划往往会牺牲经济和便利原则，在实施过程中产生浪费，因此在处理此类问题时，需要加强县市区域之间的交流合作，实现科学管理和规划。义马市、孟州市、镇平县、封丘县、淇县和睢县等县市的紧凑度较高，紧凑度值为0.684 451～0.761 976，以上县市从图形上看也较为接近圆形，因此这些行政区划的区域内部结构也更为紧密，政府的行政管理职能可以得到较好地发挥。

同时从图形上看，一些相邻县市的紧凑度值相差较大，如图7所示，例如安阳市为0.658 665，相邻的安阳县为0.384 873，而濮阳市为0.534 027，相邻的濮阳县为0.625 304，而渑池县为0.525 434，相邻的义马市为0.761 976，如果将二者的行政区划合并后重新计算紧凑度，其数值将得到提高，这一方面说明相邻两县市的合作需要更加紧密，另一方面也可以为将来的行政区划调整提供参考依据。

3 河南省县级行政区划存在问题及改革建议

通过对河南省县级行政区划形态特征分析，可以发现目前河南省县级行政区划还存在一些问题：

1)部分县级行政区划边界复杂度受省级边界和地形影响较大，复杂度越高行政管理越困难。河南省县级行政区划分形维数指标数值总体较小，这是由于河南省绝大部分地区地处平原，同时结合历史、文化、政治的共同作用，各县边界的复杂曲折程度总体较低，而其中分形维数较大的县，其边界形成受到太行山、大别山、黄河等地形因素的影响较大，曲折细节较多，因此会对行政管理效率造成一定影响。因此在将来行政区划调整时，除了需要考虑区划层级和行政中心，还需要将边界形状复杂程度考虑在内，一方面要保持历史和文化习惯，另一方面需要结合地形地貌优化边界复杂度，从而提高行政管理效率。

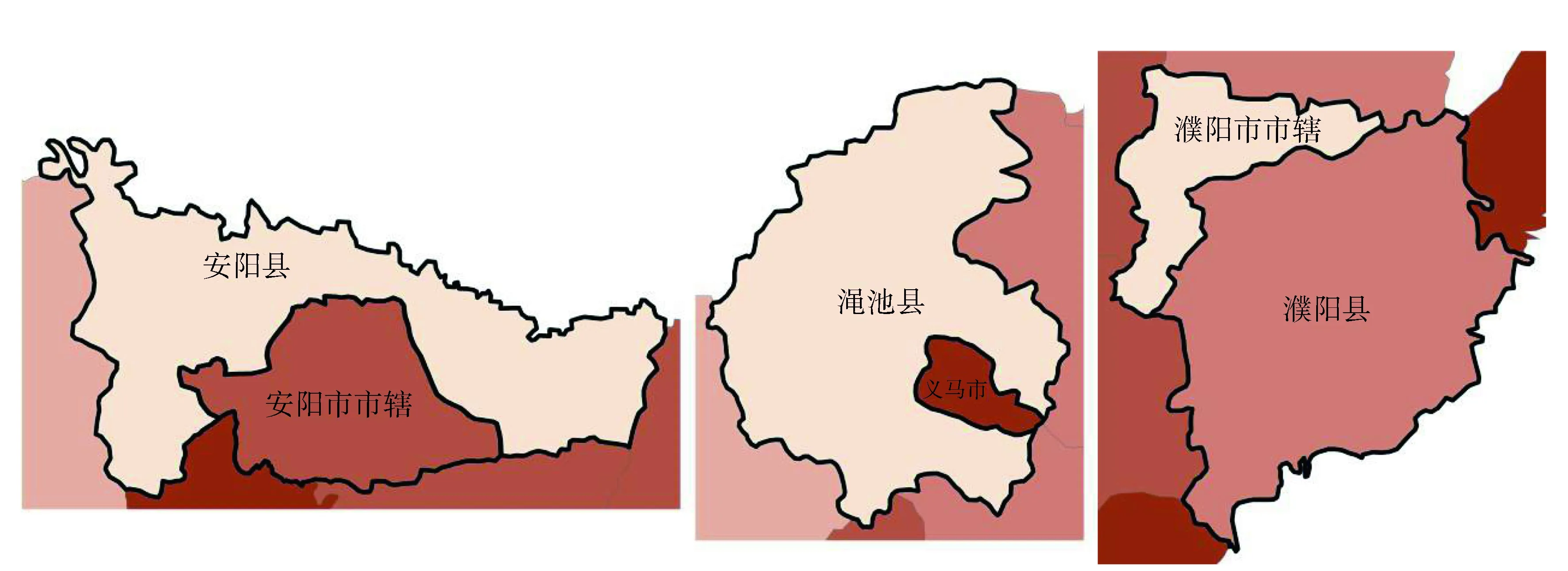
图7 相差较大的相邻县市紧凑度示意

2)行政中心边缘化，难以发挥优势带动作用。本文选取县级行政中心作为放射状指数的优势点，用以体现行政中心对该区划的辐射带动作用，优势点越靠近区域的几何中心，其行政执行效率和辐射作用越明显，图5中的放射状指数较大的几个县，其行政中心位置明显边缘化，优势点相对于边界结构松散化，从而导致行政中心进行管理时交通和通信成本增加，其辐射带动作用大大降低。因此，除了需要对行政区划边界形状进行优化调整，同时还需要对其内部结构进行优化，例如调整行政中心位置，或增设次级行政中心和经济中心，从而增强优势点辐射作用，带动区域经济发展。

3)行政区划形状空间聚集性低，提高管理效率。从行政区划紧凑度指标和其图形形状分析，某些县市的行政区划呈月牙状，与空间聚集性最高，紧凑度指标最大的圆形相去甚远，从而导致进行基础建设项目规划时，可以避开区划边界而造成规划不合理和浪费现象。因此，在目前行政区划分界状态下，需要大力加强区域间协调，以经济性和便利性为原则进行项目规划，同时还可参照紧凑度指标，对一些相邻县市进行合并，科学规划行政区划，增强区域内部联系，提高管理执行效率。

4 结 论

分形维数、放射状指数和紧凑度是对行政区划边界形状特征进行定量分析的测度方法，都有其特定适用范围和各自优缺点。通过实验可以得出分形维数与紧凑度具有较明显的相关性，而且二者较为准确地反映河南省县级行政区划的形状特征。放射状指数与二者的相关性都不十分明显，同时放射状指数的计算精度取决于辐射线数量，由于本文采用行政区政府所在地为优势点，不但避免几何中心在区域之外的问题，而且较好地反映区域优势点与边界的联系强度。

通过研究发现，河南省部分县市的空间形态特征存在边界复杂程度高、行政中心边缘化和空间聚集性低等问题，因此在将来的行政区划改革决策过程中，除了应考虑区划层级、社会经济和自然环境因素之外，还应结合定量的空间形态特征分析方法，为行政区划空间优化调整提供更加科学的理论依据。

参考文献：

[1] 王爱民, 马学广, 陈树荣. 行政边界地带跨政区协调体系构建[J]. 地理与地理信息科学, 2007(5):56-61.

[2] 熊曦, 吴冬霞, 曹姣. 关于我国“行政区经济”的思考[J]. 重庆工商大学学报, 2007(3):18-20.

[3] LEE D R, SALLEE G T. A Method of Measuring Shape[J]. Geographical Review, 1970, 60(4):555-563.

[4] BATTY M, XIE Y. From Cells to Cities[J]. Environment & Planning B Planning & Design, 1994, 21(7):31-31.

[5] 郭腾云, 董冠鹏. 基于GIS和DEA的特大城市空间紧凑度与城市效率分析[J]. 地球信息科学学报, 2009, 11(4):482-490.

[6] 郭瑛琦, 齐清文, 姜莉莉, 等. 城市形态信息图谱的理论框架与案例分析[J]. 地球信息科学学报, 2011, 13(6):781-787.

[7] 汪坚强, 朱渊, 王勇. 大城市空间形态发展模式探析——以近现代济南城市形态演变为例[J]. 城市发展研究, 2013, 20(7):90-97.

[8] 秦红岭. 当代中国城市形态问题的人文反思[J]. 中国名城, 2011(5):4-9.

[9] 冯科, 吴次芳, 韦仕川,等. 城市增长边界的理论探讨与应用[J]. 经济地理, 2008, 28(3):425-429.

[10] 王振波, 方创琳, 王婧. 1991年以来长三角快速城市化地区生态经济系统协调度评价及其空间演化模式[J]. 地理学报, 2011, 66(12):1657-1668.

[11] 程开明. 城市紧凑度影响能源消耗的理论机制及实证分析[J]. 经济地理, 2011, 31(7):1107-1112.

[12] BENGUIGUI L, CZAMANSKI D. Simulation Analysis of the Fractality of Cities[J]. Geographical Analysis, 2004, 36(1):69-84.

[13] KERSMAECKER M L D, FRANKHAUSER P, THOMAS I. Using Fractal Dimensions for Characterizing Intra-urban Diversity: The Example of Brussels[J]. Geographical Analysis, 2003, 35(4):310-328.

[14] 陈彦光, 刘继生. 城市土地利用结构和形态的定量描述:从信息熵到分数维[J]. 地理研究, 2001, 20(2):146-152.

[15] 李斌, 秦奋, 陈郁. 基于GIS的河南省地级市行政区边界形状研究[J]. 河南科学, 2009, 27(1):110-114.

[16] 王新生, 刘纪远, 庄大方,等. 中国特大城市空间形态变化的时空特征[J]. 地理学报, 2005, 60(3):392-400.

[17] 冯健. 杭州城市形态和土地利用结构的时空演化[J]. 地理学报, 2003, 58(3):343-353.

[18] SHEN Guoqiang. Fractal dimension and fractal growth of urbanized areas[J]. International Journal of Geographical Information Science, 2002, 16(5):419-437.

[19] 林炳耀. 城市空间形态的计量方法及其评价[J]. 城市规划学刊, 1998(3):42-45.

[20] BOYCE R R, CLARK W A V. The Concept of Shape in Geography[J]. Geographical Review, 1964, 54(4): 561-572.

[21] GERT R D. Environmental conflicts in compact cities[J]. Environment & Planning B Planning & Design, 2000, 27(1):151-162.

[22] MARQUEZ L O, SMITH N C. A framework for linking urban form and air quality[J]. Environmental Modelling & Software, 1999, 14(6):541-548.

[23] 刘纪远, 王新生, 庄大方,等. 凸壳原理用于城市用地空间扩展类型识别[J]. 地理学报, 2003, 58(6):885-892.

[24] 帅方敏, 王新生, 朱超平,等. 中国省级行政区边界形状的GIS分析[J]. 地球信息科学学报, 2008, 10(1):34-38.

[25] CAMAGNI R, GIBELLI M C, RIGAMONTI P. Urban mobility and urban form: the social and environmental costs of different patterns of urban expansion[J]. Ecological Economics, 2002, 40(2):199-216.

[26] PAULEIT S, DUHME F. Assessing the environmental performance of land cover types for urban planning[J]. Landscape & Urban Planning, 2000, 52(1):1-20.