自动化多面函数GPS高程拟合在既有铁路中的应用

2018-05-11花向红唐兆鹏

测绘工程 2018年6期

张伟,花向红,刘伟，唐兆鹏,4,陈鹏

(1.武汉大学测绘学院,湖北武汉 430079；2.东华理工大学江西省数字国土重点实验室，江西南昌 330013；3.株洲时代电子技术有限公司,湖南株洲 412000；4.32022部队,湖北武汉 430074)

近年来随着国家经济建设的快速稳步发展，铁路运输承担了大量的客运需求[1-2]。据2016年国家铁路局铁道统计公报显示，近年来全国铁路旅客发送量呈不断上升趋势，2016年全国铁路旅客发送量完成28.14亿人，比上年增加2.79亿人，增长11.0%。经济发展和客运需求的增加对客运线路的运输效率提出了更高的要求。国家发展和改革委员会、交通运输部以及中国铁路总公司印发的发改基础〔2016〕1536号文件的附件《中长期铁路网规划》中指出，到2020年实现邻近大中城市1～4 h交通圈，城市群内0.5～2 h交通圈，进一步提升铁路运输的效率。除了高速铁路的发展规划外，普速铁路网的建设也将进一步加强，既有线规划实施扩能改造将达到2万km。既有线的维护作业和改造提速的巨大工作量对线路控制网建设提出了更高的要求，传统全站仪测量方式只能在轨道天窗时间进行，测量效率较低[3-6]。考虑GPS静态测量的高精度，全天候优势，利用GPS静态测量建设既有线控制网，成为既有线改造控制网建设的现实需求[7]。

由于GPS静态测量的高程采用参考WGS84椭球的大地高，而施工建设通常采用基于似大地水准面的正常高，因此国内外学者和相关机构对如何将GPS椭球高转换大地高进行了大量的研究[8-10]。大面积的GPS高程拟合中常常采用基于重力场的模型，例如基于EGM2008模型的GPS高程转换[11-12]。考虑到GPS高程转换的重力场模型需要大量的重力场资料，同时既有线维护中存在大量现有水准高程控制点的实际情况，大量学者针对基于数学模型的GPS高程转换进行了研究。张小红等研究了基于Kriging统计的GPS高程拟合方法，该方法综合了移动法曲面模型和多面函数模型的优势[13]。吴迪军等研究了二次曲面函数模型GPS高程拟合在跨海桥梁中的应用[14]。于小平等研究了多项式拟合模型在GPS高程拟合中的应用[15]。目前多面函数模型中的核心点多需要根据人员经验选取[16]。本文针对多面函数核心点的自动选取进行研究，提出一种新的自动化多面函数模型。通过既有铁路的高程拟合实例证明，相比于二次曲面函数模型，新模型的拟合精度更高。

1 GPS高程拟合

近年来GPS高精度三维测量广泛地应用于工程控制网布设中，其中GPS三维坐标的大地高是相对于WGS84参考椭球的椭球高。由于工程施工采用基于似大地水准面的正常高，通常利用高精度的数学模型将GPS大地高转换为工程施工的正常高。GPS高程拟合主要包括3个步骤：

1)通过研究区域内已知控制点的GPS大地高和正常高获取高程异常，计算式如下：

δ=h-H.

(1)

式中：δ表示高程异常，h表示GPS大地高，H表示正常高。

2)假定控制点的高程异常具有空间相关性，利用高程异常和控制点的大地坐标(GPS经、纬度)或者工程平面坐标建立高程异常的数学模型。常用的模型包括二次曲面函数模型和多面函数模型等。

3)通过数学模型拟合未知点的高程异常，利用式(1)反算出未知点的正常高。

1.1 二次曲面函数模型

将研究区域的高程异常假设为一个复杂曲面，其数学模型如下：

δ=a0+a1x+a2y+a3x2+

a4y2+a5xy+ε.

(2)

式中：ai(i=0,1,…,5)表示模型的待估计参数，ε表示误差项，(x,y)表示已知点的坐标，一般取中心化归算后的坐标。二次曲面函数模型对应的误差方程如下：

v=a0+a1x+a2y+a3x2+a4y2+

a5xy-δ.

(3)

式中：v表示改正数。

假定测区内存在n个已知控制点，则误差方程的矩阵表达式如下：

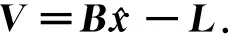
(4)

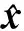
(5)

利用最小二乘可以快速解算出(4)式中的待估计参数。解算二次曲面函数模型测区内需要至少6个已知控制点。

1.2 自动化多面函数拟合模型

假定研究区域的高程异常的数学模型由多个曲面函数构成，其数学模型如下：

(6)

式中：αi表示待估计参数;θ(x,y;xi,yi)表示核函数，这里采用正双曲面函数;m表示核心点个数;(x,y)表示δ对应控制点的坐标，(xi,yi)表示选取的第i个结点。正双曲面函数计算式如下：

(7)

式中：ε2表示光滑因子，这里选取为0。

假定测区内存在n个已知控制点，选取其中m个点作为结点，则可以得到多面函数模型的误差方程矩阵形式如下：

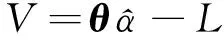
(8)

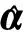
(9)

利用最小二乘可以快速计算出待估计参数建立高程异常的数学模型。

多面函数的模型中结点的选取是影响多面函数高程拟合精度的一个重要因素，为了满足既有线改造的需求，本文提出了一种自动循环选取结点的算法，其具体步骤如下：

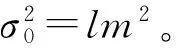
2)对于第i个结点，查找与其最邻近的两个结点，按照下式计算控制点的质量指标Qi。

(10)

式中：δi表示第i个结点的高程异常；δi1和δi2分别表示与第i个点最邻近两个点的高程异常；d1和d2分别表示第i个点与最邻近两个点之间的距离。

3)删除Qi最小的点，利用剩余的结点建立多面函数模型，其内符合精度记作σ2；

2 实验分析

为了评估分析提出的自动化多面函数模型的精度，本文利用既有线工程实例对模型进行了验证。测区内已知控制点总共为21个，选取其中8个为外符合检验点。试验中分别采用沿线路均匀选取和在线路一端均匀选取的两种策略选取外符合检验点。两种不同情况下控制点和外符合检验点的分布如图1所示。

分别采用二次曲面函数模型和自动化多面函数模型建立GPS高程拟合模型，两种情况下高程拟合模型的内符合精度和外符合精度如表1、表2所示。

图1 两种不同情况下控制点和外符合检验点的点位分布图

表1 外符合点沿线路均匀分布拟合模型的精度统计表 m

表2 外符合点沿一端均匀分布拟合模型的精度统计表 m

从表1和表2中可以看出，自动化多面函数模型的内符合精度明显优于二次曲面函数模型，其内符合精度优于0.000 5 m；自动化多面函数的外符合精度约为0.01 m，而二次曲面函数模型的外符合精度约为0.1 m;自动化多面函数的外符合精度约为二次曲面函数模型的1/10，明显优于二次曲面函数模型。同时在控制点大致均匀分布的情况下，两种情况的自动化多面函数模型的内符合精度和外符合精度均相差不大。在两种不同的外符合点分布情况下，两种模型的外符合检验误差均值，最大值，最小值分别见表3和表4。

表3，表4给出了两种模型外符合检验误差的均值，最大值，最小值。

表4 外符合点沿一端均匀分布的外符合误差统计表 m

从表3和表4中可以看出自动化多面函数模型的外符合误差的均值相比于二次曲面函数模型更接近于0，即模型的外符合误差更接近于0均值的误差分布模型。同时自动化多面函数模型的外符合误差的最大值和最小值均明显优于二次曲面函数模型。工程实例表明新提出的自动化多面函数相对于二次曲面函数模型，其GPS高程拟合的精度更高，更适用于既有线的控制网布设。

3 结论

本文研究了既有线改造提速中线路控制网布设的问题，针对两种不同的GPS高程拟合模型进行了深入探讨。利用已有既有线工程实例对新提出的自动化多面函数模型进行了精度评估分析。实验结果表明，新模型能够实现多面函数结点的自动选取，同时确保了多面函数模型高程拟合的精度。实验结果的内符合精度，外符合精度以及外符合误差的均值，最大、最小值均表明新提出的自动化多面函数模型明显优于二次曲面函数模型，其更适用于呈线状的既有线的控制网布设。

参考文献：

[1] 陈光.铁路旅客运输需求分析与对策研究[J].中小企业管理与科技,2016(16)：58-59.

[2] 崔艳萍,李艳,程文毅,等. 铁路客运发展外部环境及客运需求分析[J].中国铁路, 2014(2):9-13.

[3] 杨元明.既有铁路扩能改造若干问题探讨[J].铁道工程学报,2010(12):1-4.

[4] 方焘,刘新荣,耿大新,等. 既有线路基提速改造健康状态综合评价方法[J].西南交通大学学报,2012,47(4):591-596.

[5] 朱洪涛,徐荣.既有线三维精测技术分析[J].铁道工程学报,2009,26(1):49-51.

[6] 朱洪涛,龙辉,吴维军.一种既有线偏差约束精测网建网方法[J].铁道标准设计,2017, 61(2):20-23.

[7] 朱占荣.基于GNSS的煤矿地表移动观测系统[J].矿山测量,2015(1):59-62.

[8] 王明孝,陈建斌,赵秀杰,等.大地高误差对坐标系转换精度的影响[J].测绘工程,2013, 22(3):8-11.

[9] 张京礼,史振江,李瑞. GPS高程拟合精度探讨[J].测绘工程,2004,13(2):29-31.

[10] 郭春喜,伍寿兵.区域厘米级大地水准面的确定[J].测绘通报,2000(9):3-4.

[11] 雒养社,姚排,曲彬.基于EGM2008模型的GPS高程转换法[J].中国煤炭地质, 2013(12):79-82.