带有部分不确定性的平差算法在高程拟合中的应用

左廷英，丁俊豪，宋迎春，肖兆兵

(中南大学 地球科学与信息物理学院，湖南 长沙 410083)

GPS测量能够获得测站点高精度的WGS-84坐标，即大地经度L，大地纬度B和大地高H[1-2]。通过高斯正算公式能将大地坐标L和B转换为高斯-克吕格投影平面坐标系中的坐标(x,y)，但高程则需利用高程拟合实现，考虑到大地高与正常高的差值(高程异常)，通常的方法是以平面坐标(x,y)为自变量，高程异常值为因变量来建立拟合函数[3-4]。若仅考虑高程异常(观测向量)的误差，认为平面坐标无误差，则可直接利用最小二乘法(Least-Squares，LS)求得拟合参数。由于测量技术手段和环境因素，平面坐标必然存在误差，有时这种误差甚至是不确定的，造成法方程系数阵包含不确定性，最小二乘解不够精确。研究者针对观测向量和系数阵都含有误差的情况，提出采用总体最小二乘法(Total Least-Squares，TLS)解决[5-10]。如王乐洋等人推导了利用监测点位移或速度反演地壳应变参数的总体最小二乘方法的求解过程；陆珏在相机定标过程中，考虑像点坐标和对应地面点坐标均存在误差，采用总体最小二乘方法修正误差方程中的系数阵和观测向量，提出了更合理的计算模型。但考虑到总体最小二乘平差模型将不确定性(误差)同时融入观测矩阵和系数阵，可能导致系数阵过度修正[11]。于是，有研究者提出，引入不确定度(不确定性的度量指标)来限制不确定性。目前，在测绘领域，应用不确定度理论，研究减小不确定性的方法仍是一个新热点。如宋迎春将不确定度作为参数融入函数模型中，利用残差最大不确定度达到最小的平差准则(max-min准则)，采用迭代算法解算不确定性平差模型[12]。邹渤将前者带不确定性的平差算法成功运用于沉降AR模型中，获得了较最小二乘和总体最小二乘更高的预测精度[13]。

本文考虑到系数阵中并非所有元素都含有不确定性，针对类似于GPS高程拟合的案例，将系数阵进行分块处理[14]，对含有不确定性的区块进行限制，运用带部分不确定性的平差算法(PULS，Least-Squares with Part of Uncertainty)解算拟合参数，并与最小二乘、总体最小二乘对相同对象的解算结果进行比较，分析 PULS算法的有效性。

1 GPS高程拟合模型

目前，主流的GPS高程拟合模型是针对高程异常的曲线拟合和曲面拟合[1]。本文以二次曲面拟合为研究对象，模型为

ξ=a0+a1x+a2y+a3xy+a4x2+a5y2.

(1)

式中:ξ为高程异常值，(x,y)为高斯平面坐标，ai(i=0,1,2,3,4,5)为拟合参数。求解这6个参数，至少需要6个平面点坐标以及对应的高程异常值，若有n个观测值，则

(2)

组成误差方程V=AX-L，其中

(3)

2 高程拟合模型的部分不确定性

观测数据中常含一些不确定的附加信息或先验信息，它们的统计信息和概率分布函数无法确定。在GPS高程拟合模型中，平面坐标和高程异常值含有不确定性的量，干扰量带有不确定区间，即

(4)

‖ΔA2‖F≤α,‖ΔL‖F≤β.

(5)

融入不确定度参数α和β后，原平差模型转化为带部分不确定性的平差模型，即

(6)

在部分带不确定性的平差模型中，不确定度α和β的上限已知，即带不确定性的部分A2和观测向量L的不确定性是已知的。在总体最小二乘平差(TLS)中，系数矩阵和观测向量的不确定性都是未知的；而最小二乘平差(LS)不考虑系数矩阵的不确定性(即ΔA=0)，仅认为观测向量的不确定性未知。

在限制不确定性的情况下，对X进行参数估计，可根据文献[14]提出的min-max平差准则，使残差的不确定性达到最小，即

(7)

在上述准则下，一个类似的部分岭估计[15]为

(8)

DNP-9022恒温培养箱 上海精宏试验设备有限公司；MLS-3751立式灭菌锅 日本三洋电机公司；DZ400真空包装机 郑州星火包装机械有限公司；D90单反相机 尼康株式会社；F2038/H7001无影灯 康尔健医疗科技有限公司；UTP电子天平 上海花潮电器有限公司；FA2004分析天平 常州市幸运电子设备有限公司。

3 实验分析

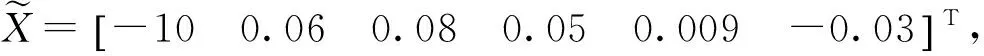
表1 模拟点坐标及其对应的高程异常值 m

图1 模拟点分布

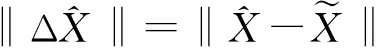
解算的拟合参数与其真值之间差值的二范数，表征解算精度见表2和图2。从表2中可以看到，带部分不确定性平差算法(PULS)解算参数的精度高于最小二乘(LS)和总体最小二乘(TLS)，差值二范数仅为0.015，而总体最小二乘平差由于系数矩阵和观测向量同时考虑不确定性，但这种不确定性的限度未知，导致了修正过度，使得结果不及最小二乘平差。为了检验所求参数的适用性，另外设置50个均匀分布模拟点进行高程异常内插，以参数真值计算的高程异常真值作为评定精度的标准。50个高程异常利用MATLAB中MESH函数绘制的三维曲面图见图3。计算的各点高程异常值分别减去对应的真值再取绝对值后绘制的折线图见图4，子图中虚线表示平均绝对差值，三种平差模型计算的参数内插高程异常得到的平均绝对差值分别为：0.56 mm(LS)、0.77 mm(TLS)和0.07 mm(PULS)，可以看到利用PULS计算的参数内插高程异常的精度较LS和TLS高一个数量级，与表2得到的结论一致。另外从图4可以看出，LS和TLS方法得到的拟合参数内插高程异常的绝对差值有呈现总体逐渐增大的趋势(随坐标的增大)，这与选取的二次曲面拟合模型有关系：带不确定性的坐标值增大，系数矩阵中的不确定性也随之增大；但PULS方法在同样的内插范围看，绝对差值却呈现减小再增大趋势，这也进一步表明PULS在一定范围内对于较强不确定性的干扰有抵抗性。

表2 拟合参数解算结果

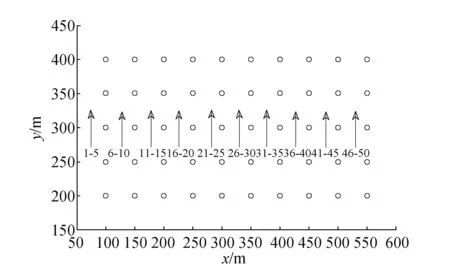
箭头表示内插点按点号排序图2 高程异常内插点的分布

图3 三组参数计算的高程异常

图4 高程异常内插值与真值的绝对差值

4 结束语

本文研究GPS高程拟合二次曲面模型的不确定性，将系数矩阵进行分块，对含有不确定性的区块加以限制，并将不确定度融入函数模型，运用带部分不确定性的平差算法(PULS)解算拟合参数。实验利用20个模拟点坐标及其高程异常值，分别运用LS，TLS以及PULS对拟合参数进行解算，结果表明，PULS得到的拟合参数精度高于LS和TLS，另外由于TLS同时考虑系数矩阵和观测向量的不确定性，但这种不确定性的限度未知，导致了修正过度，使得结果不及LS。利用解算出的3组参数，在50个均匀分布的模拟点进行高程异常内插，内插精度同样反映出PULS解算结果的优越性。

参考文献：

[1] 高原,张恒景,赵春江.多项式曲面模型在GPS高程拟合中的应用[J].测绘科学,2011,36(3):179-181.

[2] 李军海,文汉江,方爱平,等.Kriging方法结合最小二乘配置在GPS高程拟合中的应用[J].测绘科学,2011,36(1):99-101.

[3] 杨娟,陶叶青.GPS高程异常拟合的稳健总体最小二乘算法[J]. 大地测量与地球动力学,2014,34(5):130-133.

[4] 王苗苗,柯福阳.多项式曲面拟合和BP神经网络GPS高程拟合方法的比较研究[J].测绘工程,2013,22(6):22-26.

[5] 陈玮娴,陈义,袁庆，等.加权总体最小二乘在三维激光标靶拟合中的应用[J]. 大地测量与地球动力学,2010,30(5):90-96.

[6] 王乐洋.地壳应变参数反演的总体最小二乘方法[J]. 大地测量与地球动力学,2013,33(3):106-110.

[7] 王乐洋,于冬冬.病态总体最小二乘问题的虚拟观测解法[J].测绘学报,2014,43(6):575-581.

[8] 陆珏.总体最小二乘法在相机标定中的应用[J].测绘工程,2016,25(3):6-10.

[9] 余岸竹,姜挺.总体最小二乘用于线阵卫星遥感影像光束法平差解算[J].测绘学报,2016,45(4):442-449.

[10] 陈义,陆珏.以三维坐标转换为例解算稳健总体最小二乘方法[J].测绘学报,2012,41(5):715-722.

[11] 宋迎春,金昊,崔先强.带有不确定性的观测数据平差解算方法[J].武汉大学学报(信息科学版),2014,39(7):788-792.

[12] 宋迎春,谢雪梅,陈晓林.不确定性平差模型的平差准则与解算方法[J].测绘学报,2015,44(2):135-141.

[13] 邹渤,宋迎春,唐争气,等.沉降观测AR模型的不确定性平差算法[J].大地测量与地球动力学,2016,36(8):686-688.

[14] 陈晓林,宋迎春,邹渤.部分有界不确定性数据平差方法[J].大地测量与地球动力学,2015,35(1):118-121.

[15] 归庆明, 韩松辉, 隋立芬,等. 抗差部分岭估计及其在GPS快速定位中的应用[J]. 大地测量与地球动力学, 2006, 26(2):62-65.