双旋转毂式矫直机的参数研究及数值模拟
2018-05-11张保华翟富兵
张保华 翟富兵
(①新疆有色集团明苑置业管理有限公司 乌鲁木齐 830000②新疆新鑫矿业股份有限公司阜康冶炼厂 阜康 831500)
本文主要针对在矫直过程中出现的小间距弯曲,即导电棒两端的盲区,来进行数值模拟分析,通过对双旋转毂式矫直机调整转毂的转向和送料-出料差,从而来分析导电棒在矫直过程中的应力、应变分布,并对矫完的导电棒进行矫后平直度及表面热分布,以此得出合理的矫直参数。
1 双旋转毂式矫直机的有限元模型建立
有限元分析方法依靠其物理概念清晰、数学逻辑严谨、能够处理各种复杂问题而被广泛应用[1]。有限元分析法的基本思路是把结构整体划分为有限个小单元,从而以小单元内的节点力和位移作为未知量来求解。
1.1 双旋转毂式矫直机模型简化
利用DEFORM-3D软件分析电镍导电棒的矫直过程,主要为了研究导电棒在矫直过程中的应力应变变化情况。在明确目标之后对双旋转毂式矫直机进行模型简化。本文中要矫直的导电棒的规格为Φ 36×3×1350,在矫直过程中以导电棒为研究对象,与导电棒接触的矫直机零部件对导电棒进行矫直作用,所以在简化模型中需要设置送料辊、斜辊、出料辊,然后根据设计的矫直参数对导电棒、斜辊、送料-出料辊进行位置固定。因为DEFORM不能建立三维的几何模型,则通过SolidWorks建立三维模型,并按照矫直参数装配在一起,然后转化为STL格式导入DEFORM软件中。在查阅大量资料并进行计算后,将矫直机的矫直速度定为30m/min;由导电棒的直径为36mm,则在本文中近似取辊距P=380mm;而辊形中各参数为辊腰段S=4t、辊腹段S=t、辊胸段S=2t,辊子的实际长度为L=6t+2R,且t为两端矫直辊与导电棒的接触区长度,R为导电棒的半径。

图1双旋转毂式矫直机简化模型
图1 所示即为双旋转毂式矫直机的简化模型。为了达到与实际情况尽可能接近,实际矫直过程中导电棒是人为送进矫直机,则在简化模型布置中需要让电镍导电棒与送料辊有一段接触,从而实现预作用。为了让导电棒在矫直前后效果有明显对比,现统一设置矫前导电棒平直度为15mm/m。
1.2 双旋转毂式矫直机模型处理
1.2.1 材料设置及网格划分
在导电棒矫直的过程中,送料辊、斜辊、出料辊在其中的作用是矫直工具,不对其应力和应变进行分析,则可以把出料辊、斜辊、送料辊设置为刚性材料,把研究对象-导电棒设置为塑性材料,温度设置为常温,材料设置为铜。
同时,对导电棒进行网格划分时,将导电棒划分为150000个单元进行分散计算。将导电棒中容易发生严重弯曲的部位进行局部细化,网格比调整为0.05。
1.2.2 运动及体积补偿设置
DEFORM中模型的运动控制主要分为两部分:一个为直线运动设置,另一个为旋转运动设置。导电棒在矫直的过程中是没有初速度的,完全靠辊子的作用来移动,所以不对导电棒施加任何运动设置。8个平辊分别施加相同的角速度,且围绕自身中心自转。4个斜辊两两成对安装在两个不同的转毂上被施加相反的角速度,使其围绕导电棒进行公转。
在运动设置完成后,需要对材料进行补偿设置。一般而言极限应变率的值是平均应变率。极限应变率对仿真计算影响较大,如果极限应变率设置的过大会造成求解精度下降,设置的过小会使收敛困难。
1.2.3 摩擦与接触设置
本文主要研究的是导电棒在辊子的作用下弯曲变形的过程,在弯曲过程中涉及到导电棒与辊子的接触、作用、分离,并且接触问题的设置也关系到整个仿真的真实性和成功率,是一个比较难解决的非线性问题[8]。
在本文中主要涉及到的接触关系有导电棒和8个平辊的接触,导电棒与4个斜辊的接触,总共12个接触关系。DEFORM系统提供的接触关系主要有3种,分别为剪摩擦、库伦摩擦、混合摩擦,本文所定义的导电棒与平辊和斜辊之间的摩擦均为剪摩擦,但是导电棒与平辊之间的接触和导电棒与斜辊之间的接触面积、方式不同,则设置导电棒与平辊和斜辊之间的摩擦系数也不同。表1为体积补偿与摩擦系数的参数设置。

表1 主要参数设置
2 模拟结果与分析
2.1 转毂转向对矫直效果的影响
本文所研究的转毂式矫直机除了在结构上有所改变外,最主要的调整是采用两个转毂结构,即可以保证两组斜辊的旋转方向不同,使导电棒经过有效矫直区时,接触面积增大,接触轨迹不重合,从而对导电棒的小变形弯曲起到很好的矫直效果。所以下面将对转毂的转向进行重点分析,在其余结构参数和工艺参数确定的情况下,对单旋式转毂矫直过程和双旋式转毂矫直过程进行模拟仿真,单独分析转向对矫直效果的影响,在对比矫后导电棒的平直度的前提下,确定转向对矫直效果的影响作用。
设立两组转毂转向不同的矫直模型,第一组是两个转毂转向相同(统一将转毂转向设置为正),第二组为两个转毂转向相反(第一对转毂转向设置为正,第二组转毂转向设置为负),其余参数均设置相同。经过有限元模拟分析,两组导电棒按设定参数均可以正常完成矫直工作,且在矫直过程中没有出现导电棒失真变形或其他情况,两组完成的情况见图2。

图2 矫直完成情况
当把两个转毂的转向设置为相同时,即可等同于传统的转毂式矫直机,根据仿真模拟结果来分析转毂的转向对矫直过程的应力分布情况以及矫后导电棒的平直度变化。
在相同条件下对单旋转毂式矫直机和双旋转毂式矫直机进行了导电棒矫直模拟仿真,仿真过程中如图3和图4所示,选取导电棒刚好经过两个转毂的节点来分析。单旋转毂式矫直机在此时刻受到的最小应力为0.00939MPa,受到的最大应力为484MPa,面对小变形的弯曲,导电棒并未受到合适的应力。而双旋转毂式矫直机在同一时刻所受到的最小应力为20.2MPa,受到的最大应力为524MPa,在应力分布图中可以明显看到,导电棒受到了比较明显的应力变化。在图3、图4中,我们可以发现,双旋转毂式矫直机在矫直过程中使导电棒受到了比较均匀的应力变化,并且较为全面的对导电棒进行了应力覆盖。综上所述:双旋转毂式矫直机在矫直力分布以及接触面积上较单旋转毂式矫直机有很大的提高。
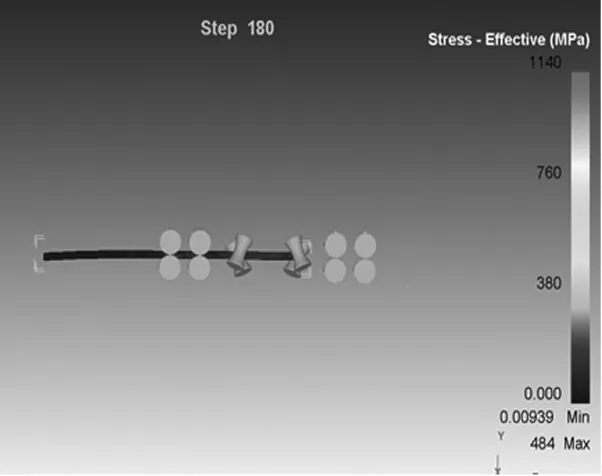
图3 单旋转毂式矫直导电棒应力分布情况
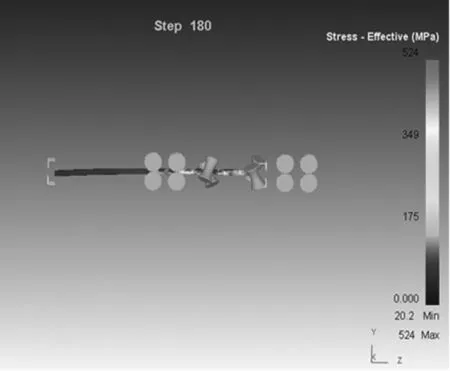
图4 双旋转毂式矫直导电棒应力分布情况
为了更方便的对导电棒的矫后平直度进行分析,现在平均的在导电棒上标识10个点,先获得这10个点的坐标,从而用线性回归法获得线性回归图得到矫后导电棒的平直度。两种不同转毂转向分布的线性回归图5、图6。
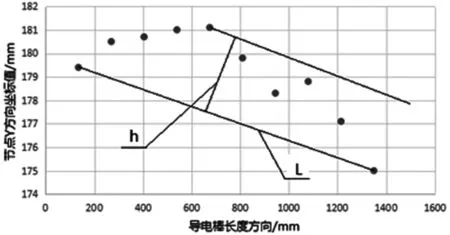
图5 单旋转毂式矫直导电棒节点分布图
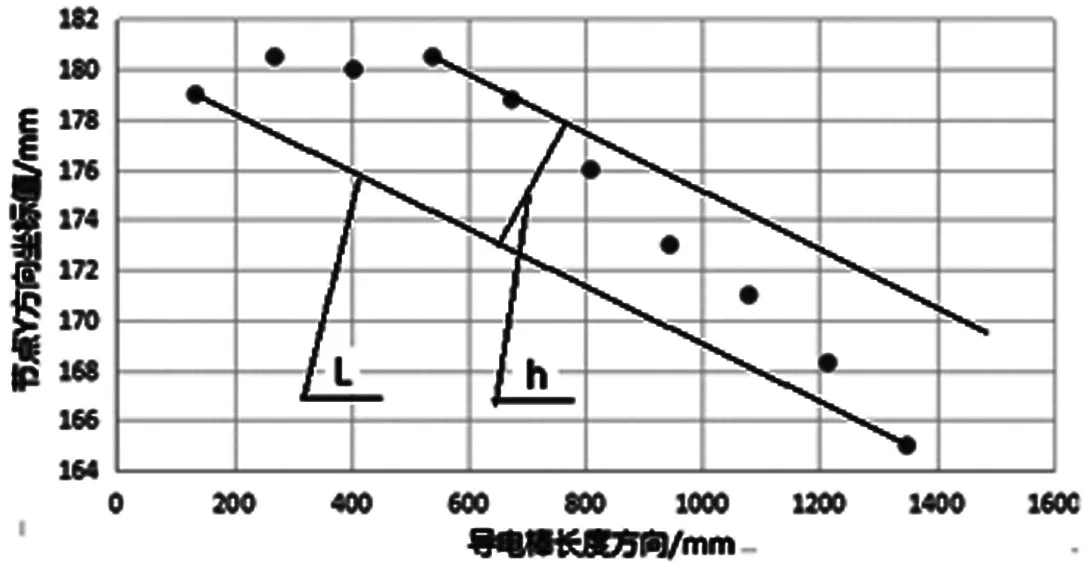
图6 双旋转毂式矫直导电棒节点分布图

图7 导电棒测量数据示意图
导电棒的近似弯曲如图7所示,其平直度与弦长L和挠度h有关,直线度的计算公式如下:
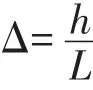
根据图5、图6按比例的原则可以计算出单旋转毂式矫直机和双旋转毂式矫直机下导电棒矫后的平直度,计算结果如下:
单旋:Δ=5.89mm/1.363m=4.32mm/m
双旋:Δ=3.54mm/1.358m=2.60mm/m
由结果可知:两种不同旋向的矫直机相比,双旋转毂式矫直机比单旋转毂式矫直机在矫直小变形弯曲方面有更好的效果。
2.2 拉料速度差对矫直效果的影响
送料速度指的是导电棒在矫直过程中,夹紧辊(送料辊)以多大的速度将导电棒送入转毂内。拉料速度指的是导电棒在经过矫直后即将走出转毂时,夹紧辊(拉料辊)以多大的速度将导电棒拉出转毂。需要注意的是夹紧辊的作用主要是将导电棒能够送入和拉出转毂并防止其发生转动,所以在连续工作时不需要很大的拉送力和夹紧力,并且送料速度和拉料速度必须能够实现无级调节。拉料速度差不仅对矫直精度能够产生影响,设置的恰当可以使工件在矫直区内形成一定的张力。所以很有必要对拉料速度差进行模拟研究。在设定转毂转向、转速等其余参数不变的情况下,设置送料-拉料速度差来进行矫直过程的模拟仿真,从而分析拉料速度差对矫直效果所产生的影响。
分别设置3组不同的拉料速度来进行导电棒的矫直模拟仿真,三组参数分别设置为:⑴送料速度=32m/min,拉料速度=30m/min;⑵拉料速度=送料速度=30m/min。⑶送料速度=30m/min,拉料速度=32m/min。经过有限元模拟分析,后两组导电棒按设定参数均可以正常完成矫直工作,即送料速度等于拉料速度、送料速度小于拉料速度的情况,且在矫直过程中没有出现导电棒失真变形或其他情况,这两组完成的情况见图8。
第一组当送料速度大于拉料速度时,导电棒在出料辊出发生了应力集中,导致导电棒在模拟过程中出现失稳情况,使导电棒出现严重的弯曲变形并接近报废,则应力分布和直线度不予讨论,情况见图8。

图8 第一组拉料速度差导电棒矫直情况
但是当送料速度等于或小于拉料速度对矫直效果的情况并不清楚,即在其余两组设定的参数下,在矫直过程中哪组的矫直应力分布的最均匀以及在矫直完成后哪种的导电棒平直度最小。图9、图10为后两组在矫直过程中的应力分布情况。

图9 第二组拉料速度差矫直导电棒应力分布情况

图10 第三组拉料速度差矫直导电棒应力分布情况
在相同条件下对三组参数进行了导电棒矫直模拟仿真,第一组发生了矫直失稳现象,其余两组的仿真过程如图9和图10所示,选取导电棒完全经过送料辊的节点来分析。当送料速度等于拉料速度时矫直机在此时刻受到的最小应力为0.982MPa,受到的最大应力为345MPa。而当拉料速度大于送料速度时,且在同一时刻所受到的最小应力为1.254MPa,受到的最大应力为425MPa,在应力分布图中可以明显看到,导电棒均受到了比较明显的应力变化。在以上两图中,我们不难发现,当拉料速度大于送料速度时,导电棒内部所受的力更加均匀,并且应力集中在拉料辊和送料辊之间,使这段导电棒产生了一定的张力。综上所述:对双旋转毂式矫直机而言,当拉料速度小于送料速度时,在一定程度上会造成导电棒失稳甚至产生事故。当拉料速度大于送料速度时对导电棒的表面应力并没有多大影响,但是会在导电棒内部产生一定的张力,有利于提高导电棒的矫直质量。
为了更方便的对导电棒的矫后平直度进行分析,现在平均的在导电棒上标识10个点,先获得这10个点的坐标,从而用线性回归法获得线性回归图得到矫后导电棒的平直度。两组不同拉料速度差矫后导电棒的线性回归见图11、图12。
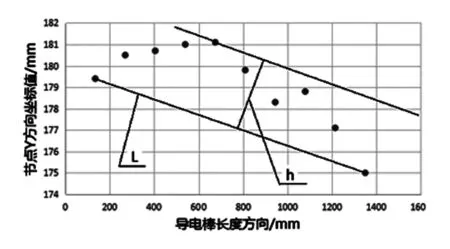
图11 第二组拉料速度差矫直导电棒节点分布图
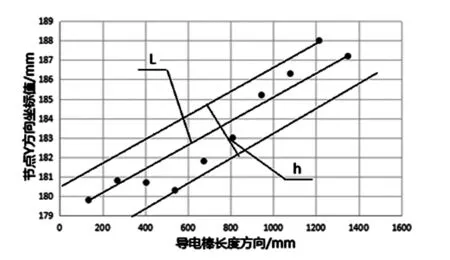
图12 第三组拉料速度差矫直导电棒节点分布图
根据图11、图12按比例的原则可以计算出按两种拉料速度差设置的导电棒矫后的平直度,计算结果如下:
第二组:Δ=3.54mm/1.358m=2.607mm/m
第三组:Δ=3.31mm/1.356m=2.441mm/m
由以上结果可知:此两组速度设置,即拉料速度等于送料速度和拉料速度大于送料速度对矫直效果的影响并不是很明显。
3 结论
通过之前的仿真分析,得到了主要矫直参数转毂转向、拉料速度差对导电棒矫直质量的影响规律,对这些参数的研究为我们提高矫直质量提供了很大的依据。
⑴从两种矫直方式的模拟结果可以发现,双旋转毂式矫直在矫直的应力分布方面和导电棒的矫后平直度方面都比单旋转毂式矫直有更好的效果,说明双旋转毂式在接触轨迹和应力分散等方面相比于单旋转毂式都有了很大的改善。
⑵从两种速度差设置的模拟结果可以发现,虽然当拉料速度大于送料速度时,矫直效果没有明显的改善,但是观察导电棒的内部应力可以发现,拉料速度大于送料速度时,导电棒内部产生一定的张力,更有利于提高导电棒的矫直效果。
[1]王富耻,张朝晖.有限元分析理论与工程应用[M].北京:电子工业出版社,2006:3-9.
[2]李树珍.棒材矫直变形过程的有限元数值模拟[D].燕山大学,2006:2-50.
[3]崔甫.二辊矫直机的理论分析与计算[J].冶金设备,1982,4(5):41-49.
[4]刘勇.二辊矫直工艺及关键技术研究[D].太原科技大学,2011:12-16.
[5]敖列伟,吴伯杰.二辊矫直原理及精度分析[J].重型机械,1997,45(6):41-46.
[6]敖列伟.二辊矫直辊面接触应力的计算[J].重型机械,2000,48(1):34-35.
[7]童切.电镍导电棒六斜辊转毂矫直机参数设计及优化[D].昆明理工大学,2016.
