宏观流动性与银行流动性相依结构分析

邓秉德，庞晓波，李 文

（1.吉林大学 商学院，长春 130012；2.吉林财经大学 统计学院，长春 130117）

0 引言

2013年前后中国经济进入“新常态”，经济增长下行压力陡增，央行此时虽然已经摒弃了“大水漫灌”式的使用调整存款准备金率的方式调控流动性，但流动性管理的态势仍然十分严峻，不断受到各种经济波动事件的冲击和挑战。2013年6月20日银行间隔夜回购利率最高达到30%，7日回购利率最高达28%，银行间拆借市场资金紧张，部分金融机构短期流动性风险突显；25日央行为符合宏观审慎要求的金融机构提供了流动性的支持才缓解了此次危机，“钱荒”事件为宏观流动性管理拉响了警钟。2014年起原本较为稳健的债券市场违约频现，据Wind统计2014年1月至2016年9月债券市场共有255家发债主体发生436起信用事件。且这三年违约资金逐年倍增，仅2016年发生的违约资金就达400多亿，涉及银行授信逾千亿；而2017年到期的信用债规模近4万亿，这对于大量授信于企业的银行系统而言潜在的风险传递效应不容小觑。受2015年末美联储加息的影响，中国自2016年7月起外汇储备连续5个月下降，外汇占款不断流失，银行系统流动性的供给面趋紧；央行在面对国际间资产价格的强对比和汇率硬约束时，银行系统所面对的流动性风险加大。

本文在分析宏观流动性与银行流动性理论模型的基础上，应用Copula模型测度了二者的相依结构和动态关系，这对于货币政策制定和宏观审慎管理都有理论与实践意义。

1 理论分析

分析宏观流动性与银行系统流动性的关联需要将银行系统的流动性作为一个整体进行分析，将货币政策、国内产出、汇率、国际收支、利率水平等各因素综合进行宏观与中观的综合分析。Ming Ming（2015）基于Atish R.Ghosh,Jonathan D.Ostry和Marcos Chamon（2014）所建立的“双重目标，双重工具”货币模型，构建了适用中国货币政策现状的模型。为便于分析流动性问题，简述模型如下。

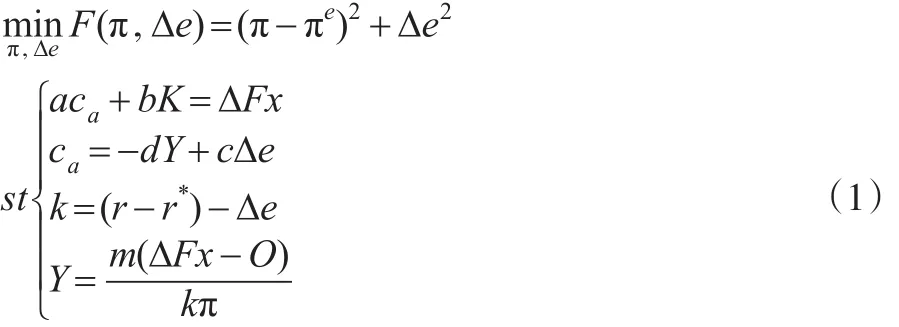
将式（2）中的约束条件代入到目标函数，令其一阶条件为0，可以求解到e*和π*。通过e*的一个解的情况可知：

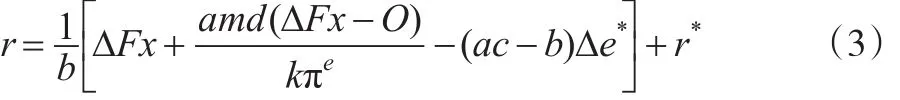
通过式（3）可以看到表征国内银行流动性水平的指标利率r受到外汇占款、通胀管理目标、基础货币投放、国际收支、国外产出等因素的综合影响，其影响机制较为复杂。还可以看出宏观的货币政策操作对国内利率的影响是掣肘于国际和国内两个方面的经济形态：一方面，央行要实现货币政策目标就要降低新增外汇占款对国内货币市场的冲击；另一方面，央行要保持汇率稳定其购买的外汇数量应当是国内外利率差乘以一个固定的倍数，即△e*=0这样才能保障汇率平稳。由此，国内利率水平r受货币政策的影响就是较为复杂的，并非总体上货币总供给数量增加，国内流动性水平就提高，利率水平就会下降。其政策传导还受制于国内和国际复杂经济状态的影响，因此，以宏观审慎视角测度宏观流动性与银行流动性有利于宏观审慎政策和货币政策的执行与完善。

2 基于Copula模型实证分析

2.1 指标选择与测度方法

本文在经济理论分析的基础上测度宏观流动性与银行流动性之间的关系，就要选择恰当的统计指标和测度方法。

（1）指标选择。宏观流动性、银行流动性、市场流动性是流动性水平的三个层次，借鉴《新帕尔格雷夫货币金融大辞典》以及相关学者的研究，宏观流动性主要体现整个经济运行和货币金融资产状况。因此其相关指标就涉及狭义货币M1、广义货币M2、外汇占款以及各类银行存款和短期债券等。综合来看，广义货币供给M2是宏观流动性中最主要的指标，此外货币供给量同实际产出存在耦合关联，因此从宏观流动性的测度上进行指标选择和设计，本文使用M2/GDP比值作为测度宏观流动性的指标；国际贸易对宏观流动性的影响则需要参考外汇占款这一指标。相应地，银行流动性主要指银行信用系统资金创造能力和流动性资产的供需动态，涉及的指标包含银行系统的存贷款利率、银行间拆借利率、债券投资与回购、信贷投放等。银行流动性需要将银行系统作为一个整体进行分析且能够反映出这个系统的资金供给状态，因而本文选择银行间同业拆放利率SHIBOR作为测度指标①数据说明：以月度工业增加值增速为参考，将此增速作为月度GDP增速计算出月度GDP，并应用X12方法剔除季节因素；考虑到银行间市场利率SHIBOR数据的起始为2006年10月，本文数据选择时间段为2006年10月至2015年12月；数据来源于国家统计局和上海SHIBOR官网。，数据时序图和图1和图2所示。

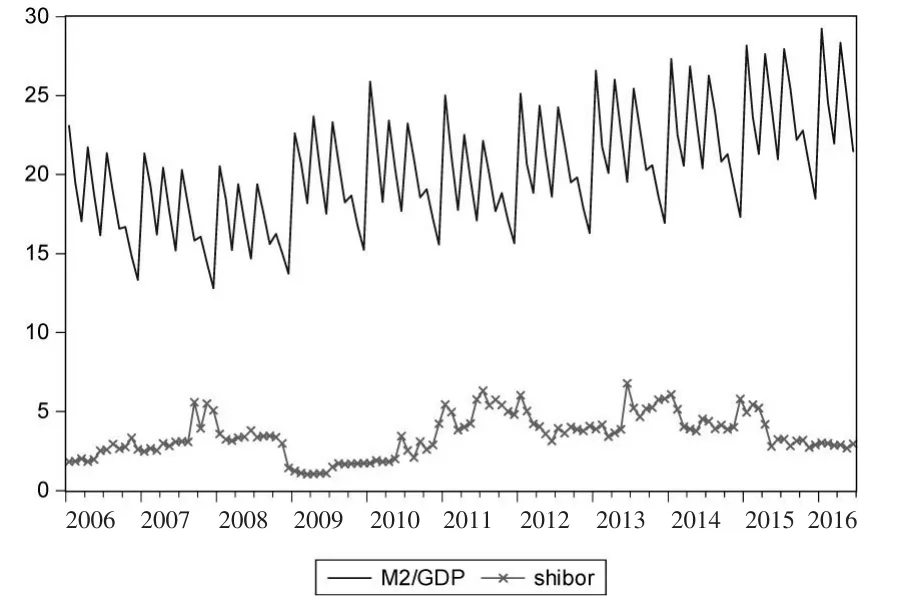
图1 月度M2/GDP和SHIBOR利率

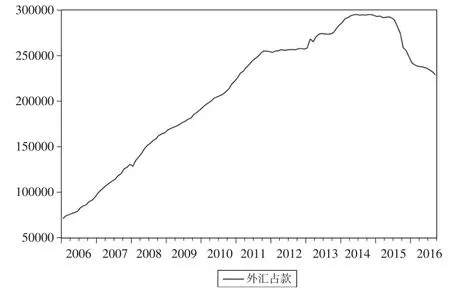
图2 外汇占款

（2）测度方法。测度两个经济变量间的关系最常用的就是线性相关系数法、Granger因果分析检验等，但这些方法在研究金融领域变量的相关性时都有一些局限性。线性相关系数法要求随机变量之间的关系是线性的，并且要求变量服从正态分布，然而金融领域变量不一定都是线性的且其相关性也不一定是正态的，往往金融时间序列通常具有“尖峰厚尾”的非正态分布特点。因此，在使用线性相关系数法来测度金融领域随机变量间非线性的相关关系就非常容易出现偏误。Granger因果分析检验法只给出了随机变量间的定性分析得结果，无法对随机变量间相依结构给出定量描述。随着Copula理论的出现与发展，上述问题得到了较好的解决，变量间的相关关系分析研究得到了进一步的发展。Copula函数概括来说是用来确定随机向量的联合分布以及多个随机变量间相依结构的统计方法。它描述了多个随机变量之间的相关性结构，使得多个随机变量的联合分布函数可以由随机变量的边缘分布和Copula函数综合来确定。早期的Copula函数可回溯到1959年Sklar的提出，SKlar定理为Copula与分布函数之间建立对等关系奠定了理论基础。本文主要基于二元Copula函数对宏观流动性与银行流动性进行相关性分析。

2.2 货币供给、经济产出与银行流动性的相依结构分析

Copula的具体理论方法本文不再赘述，下面按照Copula方法的一般步骤先分析影响影响银行流动性的国内因素（M2/GDP）与SHIBOR之间的相依关系。

（1）确定随机变量的边缘分布。确定变量的边缘分布有参数法和非参数法，先应用Jarque-Bera、Kolmogorov-Smirnov统计量分别对SHIBOR、M2/GDP序列进行检验。检验结果表明名在10%的显著性水平下，两序列均非正态分布。因此考虑应用非参数方法估计序列的边缘分布。应用ksdensity函数分别计算两序列的边缘分布，估计结果如图3、图4所示，可以看到核密度估计的结果较为理想。

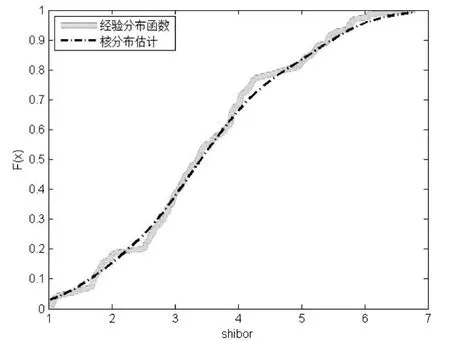
图3 SHIBOR经验分布函数和核分布估计

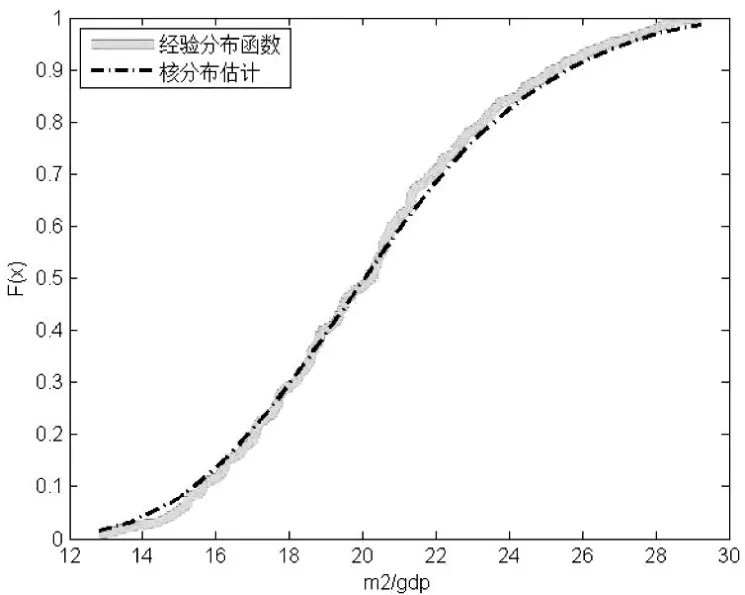
图4 M2/GDP经验分布函数和核分布估计

（2）选择适当的能够描述随机变量关系的Copula模型。应用Matlab中提供的多元正态Copula、多元t Copula、二元Gumbel Copula、二元Clayton Copula、Frank Copula等常用Copula函数对两个变量相依结构进行测度。尝试了上述常用模型后计算发现：M2/GDP同SHIBOR较适用于二元Clayton Copula模型。u和ν分别代表两个变量的边缘分布，标准模型形式为：

估计参数α=0.3，因此得到两变量的相依结构为：

（3）相依结构分析。估计得到的Clayton Copula概率密度图和等高线图参如图5和图6所示。观察估计的Clayton Copula分布可以发现服从其分布的两个变量在下尾部有更为密切的关系，而在上尾处则关联不大。而且Clayton Copula仅有下尾相关系数为2-1/α，带入α=0.3，可以计算得到尾部相关系数为0.81。Copula模型不仅测度了两个变量之间的相依结构，而且也解释了一个非常有意义的现象:银行间的流动性水平对较为充裕的宏观流动性不是非常敏感，但是当货币供应量下降或者经济下行时，宏观流动性降低对银行间的流动性就会有较为显著的影响，下尾相关系数高达0.81，很好地刻画了目前中国银行间流动性的特征。这种宏观流动性与银行流动性的下尾相关，上尾无关的实证结果也为央行货币政策的制定与执行提供了一个很好的参考依据，即央行在抑制通胀时仍要保持一定的经济增速，否则可能会对银行间流动性造成巨大冲击。

图5 Clayton Copula分布密度图

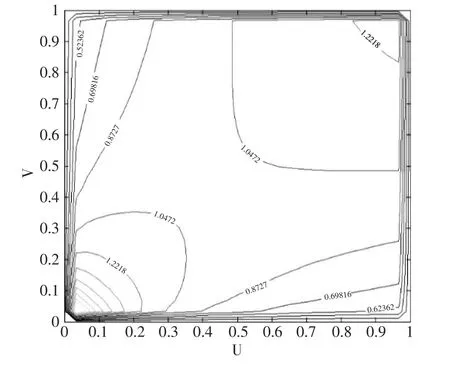
图6 Clayton Copula等高线图

2.3 外汇占款与银行流动性的相依结构分析

类似地，分析外汇占款与SHIBOR月度利率之间的相依结构。步骤和部分结果同上面的分析相近，不再赘述。首先，对两序列进行正态性检验，否定了正态性的假定。其次，应用非参数方法确定外汇占款与SHIBOR的边缘分布。计算表明应用二元t Copula模型较好地将两变量间的相依结构刻画出来。自由度为k的二元Copula可以表示为：

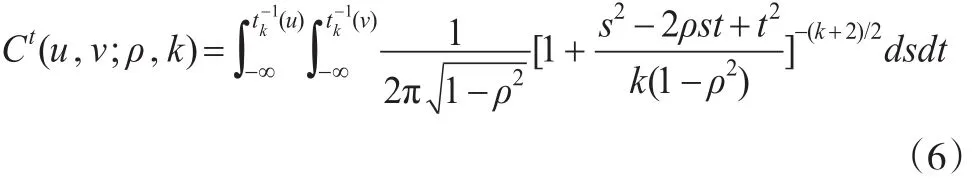
带入数据，参数估计结果为：系数ρ=0.61，自由度k=5。即有：

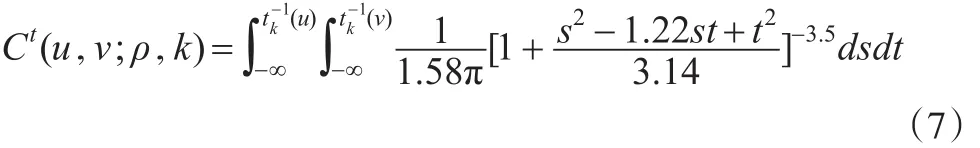
从图7和图8可以看到外汇占款同SHIBOR月度利率之间存在非常显著的二元t Copula分布形态，并且在上尾部和下尾部都有较强的关联性和对称性。

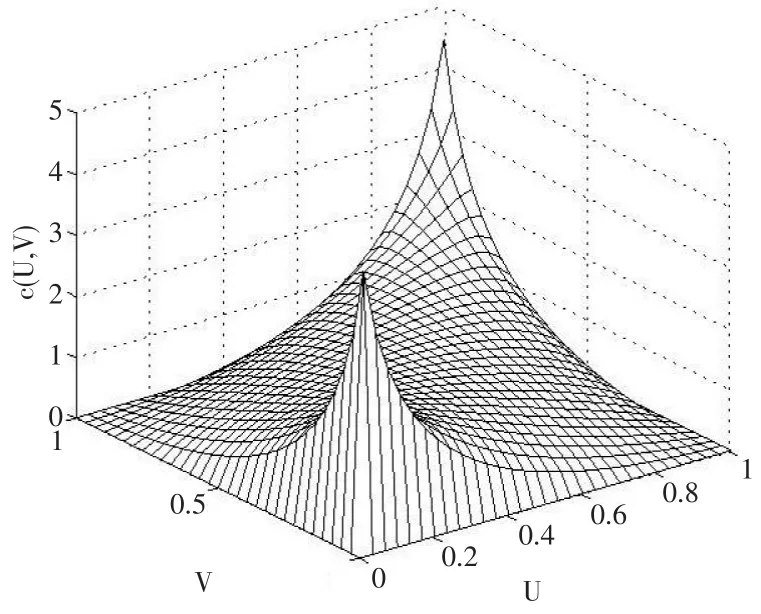
图7 二元t Copula分布密度图

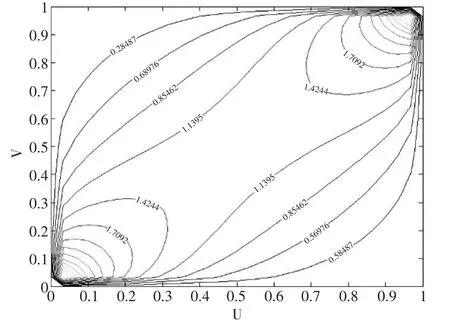
图8 二元t Copula等高线图

二元t Copula具有上尾和下尾的相关系数，其公式为：

代入参数可以计算尾部相关系数为0.28。二元t Copula模型的计算说明外汇占款对银行间的SHIBOR利率影响非常显著，外汇占款的增减对SHIBOR利率的影响是对称且双向的。当外汇占款增加时，货币供应量被动增加、银行系统资金流充裕、利率较低；当汇款占款降低时，银行系统流动性资金减少、银行系统流动性降低、利率波动较大。

2.4 模型检验

基于Copula的模型很好的测度了M2/GDP、外汇占款与SHIBOR利率之间的相依结构，反映了宏观流动性与银行流动性之间的关联关系。为了评价所应用的Copula模型的适用性，引入经验Copula。设 (xi，yi)(i=1，2，⋅⋅⋅,n)为取自二维总体(X，Y)的样本，记X，Y的经验分布函数分别为Fn(x)和Gn(y)，定义样本的经验Copula如下：

其中，I[·]为示性函数，当 Fn(xi)≤u 时，I[Fn(xi)≤u]=1，否则 I[Fn(xi)≤u]=0 。应用经验 Copula函数n(u，ν)可以计算对式（5）和式（7）的欧式距离。欧式距离较小的模型，拟合

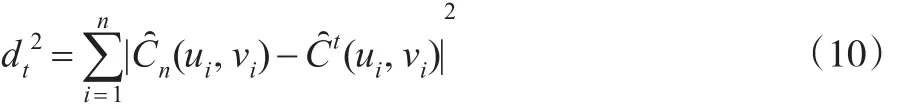
类似地，应用何种Copula模型同原数据较为理想可以进行比较分析。通过计算二元正态Copula、二元t Copula、二元Gumbel Copula、二元Clayton Copula和Frank Copula同上述两个Copula模型进行对比。欧式距离计算结果表明（见表1），所应用的Clayton Copula和二元t Copula是欧式距离最小的模型，拟合效果也是最好的，此外通过图7和图8也可以看出拟合效果较为理想。效果较优。以计算二元t Copula模型欧式距离为例，计算公式为：

表1 欧式距离计算结果

3 结论及政策建议

本文在“双重目标，双重工具”货币模型的基础上分析了银行系统流动性受宏观流动性的影响机制。在此基础上应用Copula方法测度了SHIBOR月度利率同外汇占款和M2/GDP之间的相依结构关系。宏观审慎和微观审慎的结合是目前研究的热点与难点，建立宏观流动性与银行流动性两个层面的关联关系，对于央行开展宏观审慎监管、货币政策执行以及银行系统领会央行货币政策意图都具有理论与现实意义，本文结论总结如下：

（1）M2/GDP同SHIBOR之间具有Clayton Copula相依结构关系。宏观流动性对银行流动性具有下尾相关、上尾无关的统计分布特征，这也就意味着执行宏观货币政策时要注意把握宏观流动性与银行流动性之间的关联特征。面对当前产业结构调整的宏观经济背景，银行系统积累的信贷方向错配、信贷结构错配以及信贷期限错配都可能造成银行系统在某一时期流动性的骤然紧张，央行一定要注意银行系统对宽松的流动性环境已经有些“依赖”，突然的流动性紧张就会造成类似2013年的“钱荒”冲击。

（2）外汇占款同SHIBOR之间具有t Copula相依结构关系。t Copula分布中两个变量具有上尾部和下尾部同时关联的特征。这也进一步说明了外汇占款在过去相当长一段时间提供了基础货币投放的功能：当外汇占款增加时，相当于货币供给增大，银行系统流动性增强；当外汇占款自2014年开始减少以后，银行系统流动性紧张就有所加剧。央行在制定货币政策时应当充分认识到外汇占款的“双重”作用，且由于外汇占款的变化受国际贸易影响，不由央行决定，因此央行被动接受其变化时应灵活使用“常备借贷便利”进行逆周期操作。

（3）“双重目标，双重工具”货币模型的分析也可以看到银行系统流动性水平SHIBOR受到GDP、汇率、外汇占款、M2等因素的影响，由于相关参数的不确定性，其影响机制复杂且可能为非线性。通过构建VAR模型并分析其冲击响应可以看到对SHIBOR影响最迅速的是外汇占款和M2，二者的冲击均在第2个月就达到峰值；而汇率则是在第4个月份，GDP则是在第6个月份才达到对SHIBOR的冲击的峰值。央行在进行货币政策调整时可以参考上述结果，以便在时间维度上把控其政策效应。

参考文献:

[1]End J W V D.A Macroprudential Approach to Address Liquidity Risk With the Loan-to-Deposit Ratio[J].The European Journal of Finance,2016,22(3).

[2]Claessens S.An Overview of Macroprudential Policy Tools[J].Annual Review of Financial Economics,2015,(7).

[3]王爱俭,王璟怡.宏观审慎政策效应及其与货币政策关系研究[J].经济研究,2014,(4).

[4]范小云,王道平.巴塞尔Ⅲ在监管理论与框架上的改进:微观与宏观审慎有机结合[J].国际金融研究,2012,(1).

[5]周吉人.重新认识流动性和流动性风险管理[J].宏观经济研究,2013,(9).

[6]高国华.逆周期资本监管框架下的宏观系统性风险度量与风险识别研究[J].国际金融研究，2013,(3).

[7]陈守东,孙彦林,刘洋.货币政策对流动性去向的动态影响[J].财经科学,2015,(10).

[8]彭建刚,王佳,邹克.宏观审慎视角下存贷期限错配流动性风险的识别与控制[J].财经理论与实践,2014,(4).