深基槽重力式码头地基应力分布研究及基槽开挖优化

郭隆洽，邬光远，袁 达，宋兰芳，陈 达

(1.河海大学，南京 210098；2.中交第四航务工程勘察设计院有限公司，广州 510230；3.宁波市港航管理局，宁波 315042；4.长江勘测规划设计研究院，武汉 430010)

《重力式码头设计与施工规范》(JTS167-2-2009)规定，对于背后有回填的重力式码头，基顶应力向下传递时，前肩按1：1.5扩散，后肩1：0.5扩散；此外《港口工程地基规范》(JTS147-1-2010)规定任一深度处的地基应力都呈前大后小的线性分布。有研究指出，当基床较浅时，以上规范的规定是合理的，但是当基床较深时，基床应力的扩散范围将发生较大的变化[1-5]，地基应力也并非简单的线性分布。当基槽较深时，若仍然根据以上两本规范设计基槽底宽，则基槽开挖量和砂、石的回填量将变得十分巨大，对工程造价的影响较大。因此对深基槽重力式码头地基应力的分布规律及扩散范围进行研究，并提出基槽开挖优化的方法将具有重要意义。

1 地基应力分布的一般规律

对于后方有回填陆域的重力式码头，可以将地基所受的力简化为基顶应力p1、p2、τ以及后方边载p3，其中边载包括填料的自重以及码头面的堆载，如图1所示。

图1 荷载图示 图2 模型图示

某工程断面形式如图2所示，沉箱前趾的坐标为(0,-18.5)，沉箱底宽b=17 m，抛石基床深度h=20 m，基槽宽度按照《重力式码头设计与施工规范》规定的前肩扩散至1.5d，后肩扩散至0.5d确定；下卧层为SPT达到N=40～50的硬粘土，将其作为持力层，抛石基床前后位回填砂，基槽两侧为较软的粘土。荷载大小如表1所示。土体采用Mohr-Coulomb模型，材料参数如表2所示。使用Plaxis建立有限元模型，单元选用15节点三角形平面应变单元。

通过计算，可以得到由基顶应力与后方边载引起的竖向附加应力情况如图3所示。分析计算结果可知，随着深度的增加，后方边载引起的竖向附加应力会向前趾方向扩散，而基顶应力引起的竖向附加应力会向前趾及后趾两个方向扩散。在较浅处，是以基顶应力引起的竖向附加应力主导的，沉箱宽度范围内有明显的“峰”形，随着深度的逐渐增加，后方边载的影响相对来说逐渐变明显，“峰”形越来越不明显，直至最后消失。在较浅处，前趾处的竖向附加应力比后趾处大，随着深度的增加竖向应力分布越来越均匀，在较深处，后趾处的数值可能反而比前趾处大，且沉箱宽度范围内的峰值就出现在后趾处。

表1 荷载大小Tab.1 Load value kPa

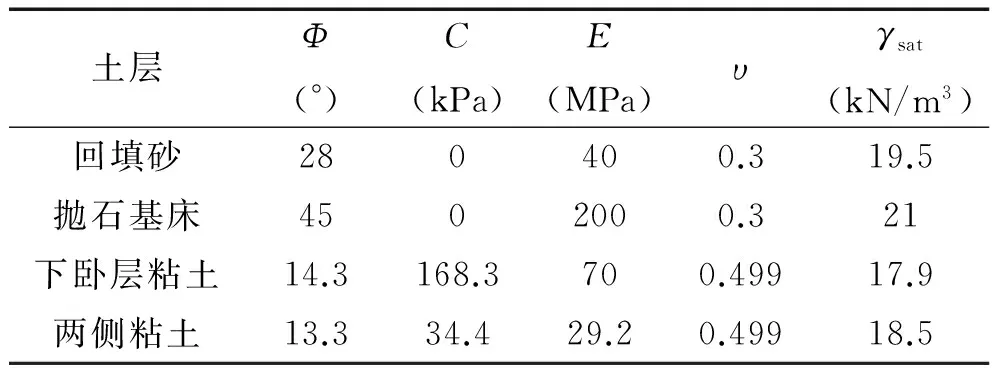
表2 土体参数Tab.2 Basic indices of soils

3-a 由基顶应力与后方边载产生 3-b 由后方边载产生 3-c 由基顶应力产生图3 各深度处的竖向附加应力Fig.3 Curves of vertical additional stress at the corresponding depth

改变地基的地质条件，将基槽两侧土体的弹性模量分别设置为30 MPa，60 MPa，100 MPa，将下卧层土体的弹性模量分别设置为70 MPa，250 MPa，500 MPa，可以得到5 m和20 m深处的竖向附加应力分布，如图4～图5所示。可见，基槽两侧和下卧层土体的弹模对地基应力分布的影响不大。

4-ah=5m4-bh=20m5-ah=5m5-bh=20m图4 各深度处不同基槽两侧土体弹模对应的竖向附加应力Fig.4Curvesofverticaladditionalstressofthecorrespondingdepthandyoung'smodulusofthestratumoutsidethetrench图5 各深度处不同下卧层土体弹模对应的竖向附加应力Fig.5Curvesofverticaladditionalstressofthecorrespondingdepthandyoung'smodulusofthestratumbelowthetrench

改变模型所受的荷载。将基顶应力的偏心距分别取为0.7 m、1.4 m及2.8 m，将基顶应力的荷载分布范围分别取为10 m、17 m及25 m，将基顶切向荷载τ分别取为70 kPa、100 kPa及130 kPa，将后方边载p3分别取为234 kPa、264 kPa及294 kPa，可以得到各情况下深度为5 m和20 m处的竖向附加应力分布，如图6～图9所示。可见，在较浅处，附加应力峰值随着基顶应力偏心距、分布范围及切向荷载的增大而增大，且峰值位置会随之往前趾处偏移。但是在不同荷载及地质条件下，地基应力分布的大致规律仍然如本节第三段所述。

6-ah=5m6-bh=20m7-ah=5m7-bh=20m图6 各深度处不同基顶应力偏心距对应的竖向附加应力Fig.6Curvesofverticaladditionalstressofthecorrespondingdepthandeccentricitiesofthebaseload图7 各深度处不同基顶应力分布范围对应的竖向附加应力Fig.7Curvesofverticaladditionalstressofthecorrespondingdepthandrangesofthebaseload

8-ah=5m8-bh=20m9-ah=5m9-bh=20m图8 各深度处不同基顶切向荷载对应的竖向附加应力Fig.8Curvesofverticaladditionalstressofthecorrespondingdepthandtangentialload图9 各深度处不同后方边载对应的竖向附加应力Fig.9Curvesofverticaladditionalstressofthecorrespondingdepthandrearsurcharges

2 地基应力扩散范围

已有研究在定义地基应力扩散角的时候，通常只是取一个定值或者粗略地确定荷载消散较快的地方，没有一个定量的标准[1,6-7]。所以可以确定一个考虑沉降和地基承载力计算的确定标准。

在进行地基沉降计算的时候，《港口工程地基规范》中规定对于一般的土质地基压缩层的计算深度应该按σz=0.2σ自重来控制，即当附加应力达不到土层自重应力的20%这个标准的时候可以认为应力水平较低可以忽略。从图3可以看出附加应力从前趾处向前会从一个较大值逐渐减小，到达某一位置后会达到此深度土层自重的20%，越过这个点后数值会继续减小。所以就沉降计算来说将这个点定义为这一深度处附加应力的消散点是比较合适的，这样荷载的分布范围就是从消散点往后的范围。而对于承载力计算来说，以某一深度为计算面，从这一深度直至泥面范围内土层的自重可以认为是一种边载，可以增加围压，起到有利作用，将附加应力的消散值定义为与土层自重相关的一个值也是合理的[8]。

图10 地基应力扩散图Fig.10 Diagram of foundation stress diffusion

如图10所示，按照以上方法，将模型从基顶至基槽底部范围内每一深度处(间隔1 m)的应力消散点，即附加应力数值等于此深度土层自重应力20%的点，在图中标出来，并将基顶前趾处与基底的消散点用直线连接起来，即可以得到模型在基顶应力与后方边载作用下的应力扩散线，应力扩散线与竖直方向的夹角即为应力扩散角，为42.8°。可以看到在应力消散点随着深度的增加，往x方向的增加减缓，在较深处甚至会有所减小。虽然应力消散点会落在应力扩散线的外侧，但是仍然处于抛石基床的范围内，不会影响到基槽外侧的土体，也就是说以这种方式应力扩散线的定义是合理的。

改变基槽深度，分别取为3 m、5 m、10 m、15 m和20 m，并改变模型所受的荷载及地基的地质条件，通过有限元模型的计算可以求得荷载、地质条件和基槽深度对地基应力扩散角的影响情况，如表3和图11所示。

表3 不同荷载条件及地质条件对应的应力扩散角Tab.3 Stress diffusion angle of the corresponding load and geologic parameters

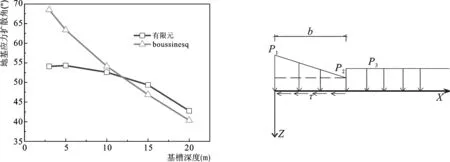
图11 扩散角随基槽深度的变化Fig.11Curvesofthevariationofstressdiffusionanglewiththetrenchdepth图12 基顶应力与码头后方边载作用下建立的坐标系Fig.12Coordinatesystemofbasestressandrearcharge

通过分析可知，基床深度在5 m以内时，有限元法算得的扩散角与《重力式码头设计与施工规范》规定的56.8°较接近，而根据Boussinesq解算得的扩散角比有限元法大。深度在5 m以上时，扩散角随着基槽深度的增加而减小，与上述规范的规定差别较大；并且在较深处，根据Boussinesq解算得的扩散角与有限元法差别不大；此外，地基应力扩散角对下卧层和基槽两侧土体的弹模以及后方边载不敏感，对基槽深度以及基顶应力大小、分布范围、偏心距、切向荷载较敏感，而在其中对偏心距相对不敏感。这也说明了在通常的计算方法中忽略荷载影响的做法可能存在问题。

3 地基应力分布的确定方法

首先考虑将地基当成均质线弹性材料，利用Boussinesq解求解应力场。由于码头的纵向长度l相比横向宽度b较大，l/b≥10，所以将其视为平面问题进行计算所导致的误差很小，完全为工程所允许。将Boussinesq解[9-10]沿码头纵向(无限长)积分，再沿码头横向积分，则可以得到条形基底均布荷载、三角形荷载及切向荷载作用下地基竖向附加应力。如图12所示，将地基所受的荷载分解为三角形分布荷载p1-p2，有限宽度的均布荷载p2，无限宽度的均布荷载p3以及切向荷载τ。根据图12的坐标系对公式进行坐标变换，则可以得到地基中任一点(x,z)的竖向附加应力，如式(1)～式(11)所示。

由图4～图5可知，基于Boussinesq解的理论解与有限元法的算得的竖向附加应力分布趋势相同，且在数值上也差别不大，所以可以考虑以此确定地基应力的分布。

σZ=σp2+σp1-p2+στ+σp3

(1)

σp2=Kp2p2

(2)

σp1-p2=Kp1-p2(p1-p2)

(3)

στ=Kτpτ

(4)

σp3=Kp3p3

(5)

(6)

(7)

(8)

(9)

m1=x/b

(10)

m2=(b-x)/b

(11)

由于式(1)～式(11)的表达式较复杂，所以，如图13所示，可以取如下4个关键点来确定指定深度处的竖向附加应力分布：A前趾位置、B后趾位置1、C后趾位置2、D消散点。其中D点位置按照应力扩散角θdiffusion来确定。

(12)

pB=px=b

(13)

pC=p3

(14)

pD=0.2σ自重

(15)

xD=-z·tan(θdiffusion)

(16)

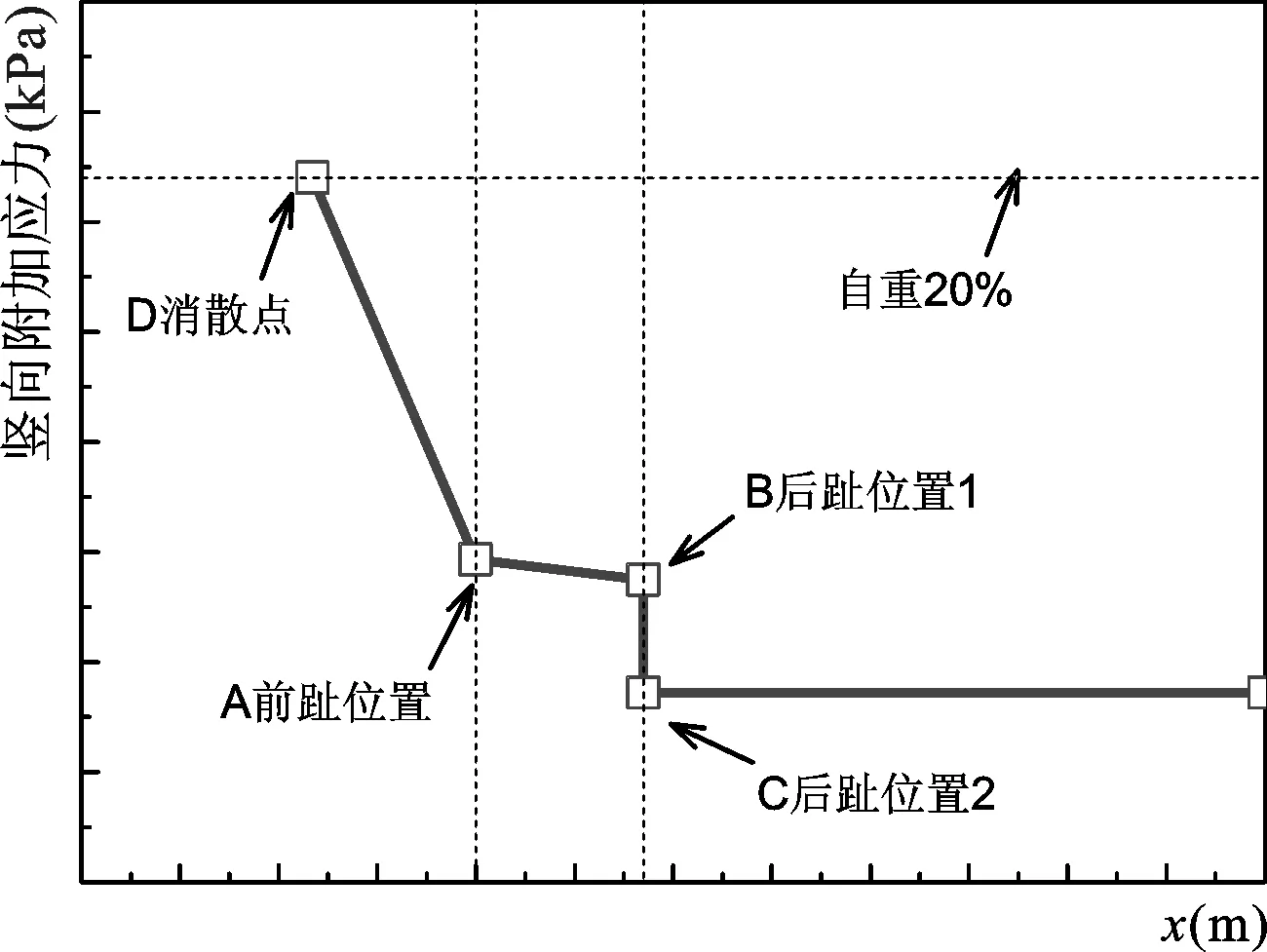
图13 简化计算方法各关键点示意图Fig.13 Diagram of the control points in simplified method

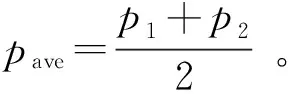
下面采取《港口工程地基规范》中规定的方法、有限单元法、文献方法1[11]、文献方法2[6-7]以及本文提出的计算方法进行计算，可以得到各深度处由基顶应力与后方边载引起的竖向附加应力如图14所示。

14-ah=2m14-bh=5m14-ch=10m14-dh=20m图14 各计算方法在各深度处的竖向附加应力Fig.14Curvesofverticaladditionalstressofthecorrespondingcalculationmethodsanddepths

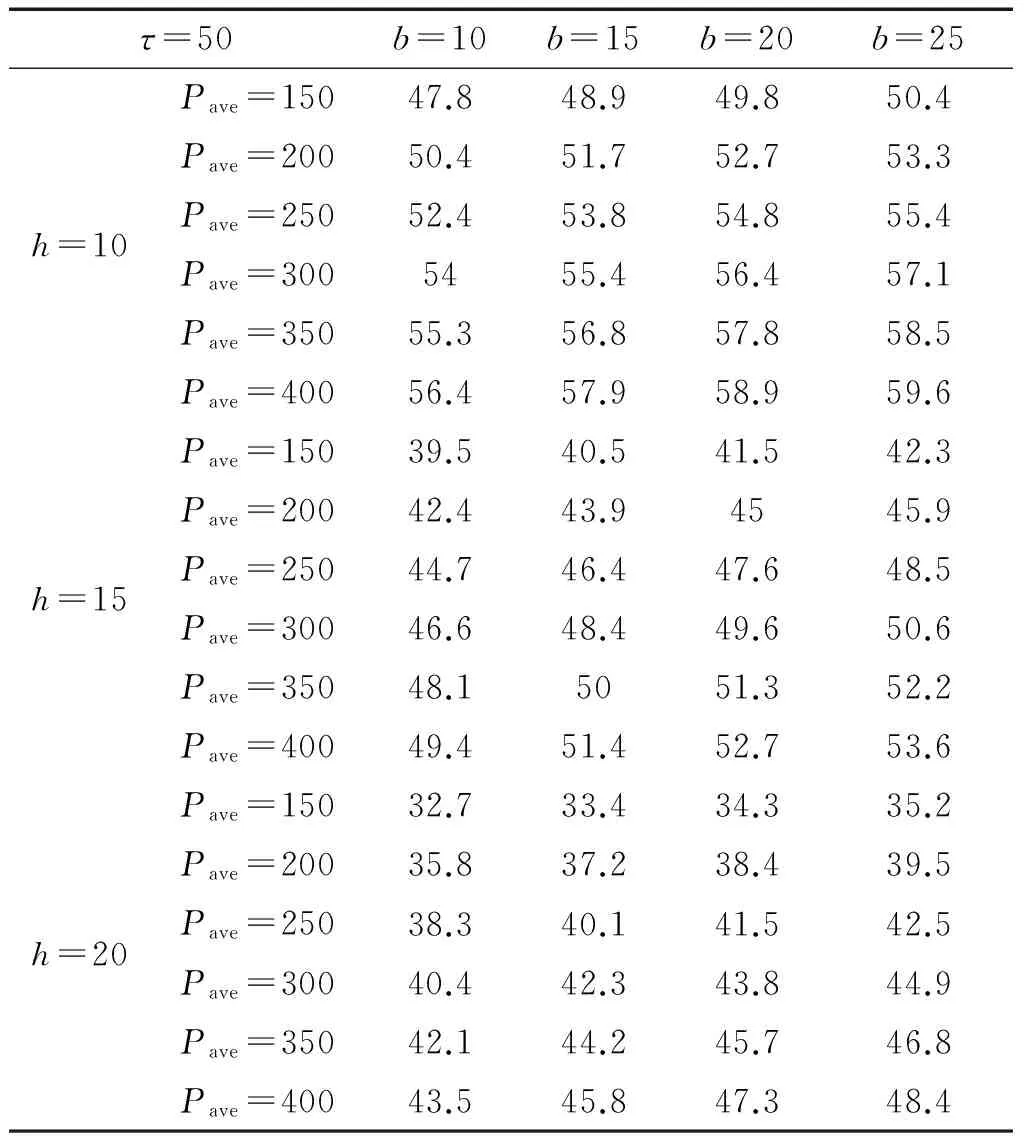
表4 地基应力扩散角θdiffusion(1)Tab.4 Stress diffusion angle θdiffusion(1)

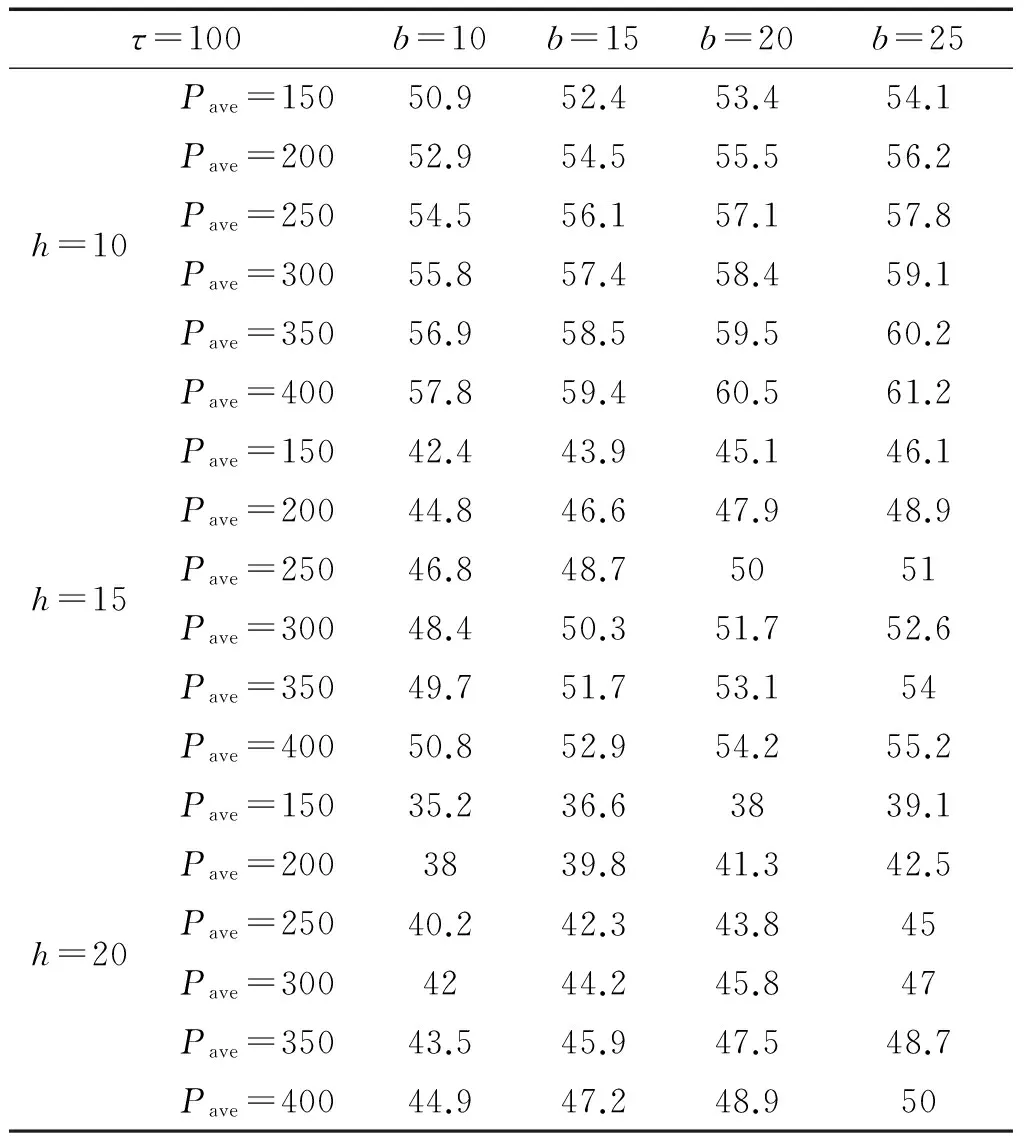
表5 地基应力扩散角θdiffusion(2)Tab.5 Stress diffusion angle θdiffusion(2)

当基槽深度小于5 m时，几种方法的计算结果比较接近。当基槽深度大于5 m后，《港口工程地基规范》规定的方法和文献方法1可能会高估抛石基床对应力的扩散能力，地基附加应力的大小明显偏小，且分布形态与其他几种方法有较大的差别；此外，随着深度的继续增加，实际地基应力扩散范围与上述规范的差别将逐渐增大，如图11所示。因此，深度大于5 m的基槽可以认为属于深基槽，此时按照《港口工程地基规范》计算地基应力将带来一定的误差。

由图14可见，在各深度处本文简化计算方法、文献方法2和有限元模型的结果相差较小，说明本文简化计算方法具有一定的可行性。其中，文献方法2的后趾处地基应力可能会有所低估。

4 基槽开挖优化设计方法

国外相关标准，如欧标《Code of practice for geotechnical design》和日标《Technical standards and commentaries for port and harbour facilities in Japan》等，并未规定基槽开挖宽度，而只要求地基承载力和沉降满足要求。此外，现有的一些研究[1-5]和本文研究也表明基槽的开挖方案存在优化的空间。一方面可以按照本文提出的应力扩散角θdiffusion来确定基槽的底宽，另一方面还可以不按照应力扩散范围来开挖，进一步减小基槽底宽。

图15 窄基槽模型Fig.15 Schematic diagram of model with a narrow trench

为了对基槽较窄，不按应力扩散范围开挖时的地基应力分布进行研究，将基槽的底宽取为基顶宽度加上前后各3 m的富余宽度，模型如图15所示，荷载大小如表6所示，通过计算可得到地基应力分布情况如图16所示。

表6 荷载大小Tab.6 Load value kPa

可见当基槽宽度较小时，会在底宽范围内产生应力集中现象，而基槽两侧土体中的应力分布与基槽较宽时的差别不大，即本文简化计算方法可以用于计算基槽两侧土体中的应力分布。此外，基槽两侧中的地基应力值较大，有必要进行地基承载力的验算。

若令模型的基槽分别向前加宽4 m、8 m，向后加宽7 m(按《重力式码头设计与施工规范》规定的1：0.5扩散线确定)，则可以得到其地基应力分布情况如图17～图18所示。

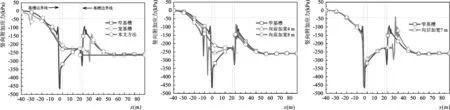
图16 各情况下深度h=20m处竖向附加应力Fig.16Curvesofverticaladditionalstressatcorrespondingsituationsat20mdepth图17 基槽向前加宽时深度h=20m处竖向附加应力Fig.17Curvesofverticaladditionalstressat20mdepthwhenthetrenchiswidenedforward图18 基槽向后加宽时深度h=20m处竖向附加应力Fig.18Curvesofverticaladditionalstressat20mdepthwhenthetrenchiswidenedbackward

可见当基槽向前加宽时可以显著减小基槽底宽范围内的应力集中现象，而基槽向后加宽时对地基应力分布的影响不大。这点可以为不按照应力扩散范围设计基槽底宽时提供参照。

5 结论

本文对深基槽重力式码头的地基应力进行分析，得到以下结论：

(1)在较浅处，前趾处的竖向附加应力比后趾处大，随着深度的增加竖向应力分布越来越均匀，在较深处，后趾处的数值可能反而比前趾处大。

(2)地基应力扩散范围受荷载及基槽深度的影响，当基槽深度大于5 m后，地基应力扩散角会比《重力式码头设计与施工规范》规定的小。本文提出了相应基槽深度和荷载下的地基应力扩散角建议值，可以据此进行基槽的开挖。

(3)本文简化计算方法的地基应力扩散范围和地基应力值与有限单元法差别较小，具有一定的可行性。深度大于5 m后，《港口工程地基规范》规定的方法会高估地基应力扩散范围而低估地基应力值，且无法正确反映地基应力的分布形态，此时建议采用本文简化计算方法来确定地基应力分布。

(4)当不按照应力扩散范围设计基槽底宽时，需要对基槽两侧土体的地基承载力进行验算；同时需要注意基槽底宽范围内的应力集中现象，可以考虑向前加宽基槽底宽来减小这种应力集中现象。

参考文献：

[1] 关兴. 重力式码头暗基床应力扩散特征分析[J]. 水运工程, 2014(8): 66-70.

GUAN X. Diffusion characteristics of subgrade stress of gravity wharf′s rubble bed [J]. Port & Waterway Engineering, 2014 (8): 66-70.

[2] 金文龙. 广州南沙港区二期码头结构设计难点与对策[J]. 水运工程, 2009 (7): 112-117.

JIN W L. Difficulties and solutions in wharf structural design of Guangzhou Nansha Port Area Phase II project [J]. Port & Waterway Engineering, 2009 (7): 112-117.

[3] 张炜煌. 超深基槽重力式码头结构选型与设计关键技术[J]. 水运工程, 2014 (4): 52-56.

ZHANG H W. Key technologies of structure selection and design for ultra-deep foundation trench gravity quay[J]. Port & Waterway Engineering, 2014 (4): 52-56.

[4] 卢少彦. 重力式码头换填基槽开挖底宽优化设计探讨[J]. 工程建设与设计, 2012 (10): 141-144.

LU S Y. Discussion on optimization design of replacement foundation trench′s excavation width on gravity quay[J]. Construction & Design for Engineering, 2012 (10): 141-144.

[5] 刘华如. 超深基槽重力式码头结构选型和设计关键技术[J]. 科技资讯, 2015, 13(8): 82-82.

LIU H R. Key technologies of structure selection and design for ultra-deep foundation trench gravity quay[J]. Science & Technology Information, 2015, 13(8): 82-82.

[6] 秦川. 重力式码头抛石基床应力分析[D]. 天津: 天津大学, 2007: 88-93.

[7] QIN C, BIE S A. Stress distribution in rubble bed of gravity wharf[J]. Port & Waterway Engineering, 2014(3):103-108.

[8] 李建国, 王珣, 孙立勋. 复合地基下卧层附加应力实用计算方法研究[J]. 铁道工程学报, 2015, 32(10): 32-37.

LI J G, WANG X, SUN L X. Research on the practical calculation method for additional stress in substratum of composite ground[J]. Journal of Railway Engineering Society, 2015, 32(10): 32-37.

[9] Love A. The Stress Produced in a Semi-Infinite Solid by Pressure on Part of the Boundary[J]. Philosophical Transactions of the Royal Society A Mathematical Physical & Engineering Sciences, 1929, 228(659-669): 377-420.

[10] 王甲春, 陈峰. 地基中附加应力分布规律分析[J]. 湖南科技大学学报:自然科学版, 2014 (4): 65-68.

WANG J C, CHEN F. Analysis of foundation additional stress distribution[J]. Journal of Hunan University of Science & Technology:Natural Science Edition, 2014 (4): 65-68.

[11] 只红茹. 重力式码头厚抛石基床稳定性研究[D]. 天津: 天津大学, 2006.