大尺度结构波浪力计算研究
2018-05-10刘清君王登婷
张 胡,刘清君,王登婷
(1.中铁大桥勘测设计院集团有限公司,武汉 430050;2.南京水利科学研究院,南京 210029;3.水文水资源与水利工程科学国家重点实验室,南京210098)
近年来,我国跨海桥梁发展迅速,相对于内河桥梁,跨海桥梁所处水文环境更为复杂,波浪荷载是基础设计必须考虑的荷载之一。目前有关基础波浪力的计算,工程应用中主要采用两类方法,一类是Morison方程,该方法主要针对小尺度结构物(D/L<0.2),此方法经过多年的发展,研究成果较多,已较为成熟[1];另一类为绕射理论计算方法,该方法主要针对大尺度结构物(D/L≥0.2),通过计算波浪场的绕射势,进而得到结构物所受的波浪力,但由于数学上的困难,仅对几种简单几何形状的物体得到了精确的解析解[2],对于复杂的结构物则需通过数值模拟法进行计算。
跨海桥梁基础多采用桥墩-承台-群桩形式,承台结构尺寸往往较大,多属于大尺度,且承台结构形式多种多样,因此有必要开展对任意截面形状的大尺度结构波浪力计算的研究。近年来,随着计算机模拟技术的进步,基于N-S方程的波浪力计算方法得到了发展[3-6]。但此方法需要建立专门的数值模型,计算周期长,工程应用受到限制。本文拟基于绕射理论,采用边界元法,建立三维大尺度结构波浪力计算的数值模型,该数学模型具有计算效率高,便于工程应用的特点。
1 基本方程
假定流体无粘性、不可压缩、做无旋运动,在静水面处,建立如图1所示的oxyz坐标系。基于线性绕射理论,扰动后的新波动场中任一点的速度势Φ
Φ(x,y,z,t)=Re{[ΦI(x,y,z)+ΦS(x,y,z)]e-iωt}
(1)
式中:Re( )表示取复数表达式的实部;ΦI为入射波复速度势;ΦS为绕射波复速度势;ω为入射波角频率;i为表示复数。
入射波势ΦI(x,y,z)具有下述形式[7]
(2)

图1 大尺度柱状结构物波浪场示意图Fig.1 Sketch of wave field for large scale columnar structure
式中:H为波高;k为波数;β为波浪的入射角;d为水深。
绕射波速度势ΦS(x,y,z)利用三维源汇分布法求解[4],即若结构物湿表面上的点源M(ξ,η,ζ) 的源强函数f(ξ,η,ζ)是连续的,则波动场中任一点q(x,y,z)的绕射势ΦS(x,y,z)为结构物表面上所有点源对q点所引起的源势之和
(3)
式中:(x,y,z)表示计算点坐标;(ξ,η,ζ) 表示物面上变化点的坐标;f(ξ,η,ζ) 为结构物表面上的源强度函数;G(x,y,z;ξ,η,ζ)为Green函数。
由式(3)可知,若要得到波动场中任一点的绕射势,就必须求解出函数G(x,y,z;ξ,η,ζ)和f(ξ,η,ζ)。其中,Wehausen[8]找到了满足条件的Green函数
(4)
式中:v=ω2/g=kthkd;r=[(x-ξ)2+(y-η)2+(z-ζ)2]1/2;J0(kr)和Y0(kr)分别为零阶第一类和第二类Bessel函数;K0(μmr)为零阶第二类修正Bessel函数,μm为方程μmtan(μmd)+v=0的正实数根。
源强函数f(ξ,η,ζ) 是由结构物表面S上流体运动的边界条件决定的,即
(5)
将式(2)、(3)代入式(5)则有
(6)

(7)
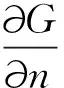
(8)
将结构物表面S离散化为N个面积单元△Sk(k=1,2…,N),以每个面积单元的形心点(xj,yj,zj)作为控制点j(j=1,2…,N),求出该点的源强函数,并用该点的源强函数值代替整个面积单元的源强函数值。
则式(6)离散化后可写成
(9)
由式(9)可写出N个方程的线性方程组,其简化写法为
(10)
式中:
(11)
将式(10)写成矩阵形式为
[f]=2[α-I]-1[Un]
(12)
式中:I为单位矩阵。
离散化的式(3)表示为
(13)
写成矩阵形式为
[ΦS]=[β][f]
(14)
当求得结构物表面上的入射势和绕射势后,作用在每一面积单元上的波浪力可由Bernoulli方程计算得到
(15)
于是,沿湿表面对压强积分得到作用在结构上的波浪力的水平分量和力矩为
(16)
(17)
2 数学模型的建立与验证
2.1 模型的建立
基于上述理论,建立计算任意截面形状大尺度结构物波浪力的数学模型。在模型建立过程中遵循以下思路:
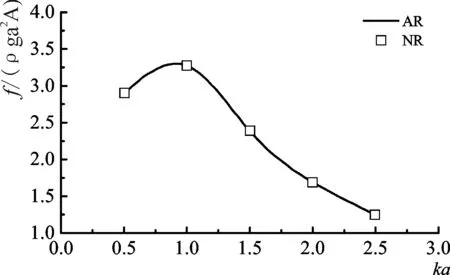
图2 圆柱墩结构波浪力对比Fig.2 Comparison of cylindrical wave forces acting on the pier structure
(1)计算结构物的几何参数,包括划分的单元数N、每一小平面单元的面积ΔS、每个单元形心点i的坐标(xi,yi,zi) 以及其单位外法线的方向余弦(nxi,nyi,nzi)等;
(2)计算两个系数矩阵[α]、[β]和列矢量[Un];
(3)求出源强度f,进而得到每一面积单元形心i处的绕射势Φsi;
(4)计算结构物表面S上每一面积单元形心处的压强pi,进而得到整个结构物上的总波浪力F和力矩M。
2.2 模型的验证
采用本文方法对一均匀圆柱进行了数值计算,并将数值计算结果(NR)与MacCamy & Fuchs的解析解进行了比较。圆柱直径为a,水深d=a。从图 2中可以看出两者吻合良好。

图3 SR40#墩围堰示意Fig.3 Sketch of SR40 # pier cofferdam
3 波浪力的测量与估算
3.1 波浪力测量概况
2015年9月29日,中铁大桥局对在建平潭海峡公铁桥SR40#墩围堰进行了波浪压强测量,期间有台风杜鹃出现,且同步观测桥墩附近风、流、波浪等要素内容。波浪要素实测值如表2所示,由于围堰所受波浪力非常大,直接测量其受力是非常困难的,故本次采用间接方法测量围堰所受的波浪力,即通过围堰压强的测量间接得到围堰所受波浪力。

表1 实测期间风向角度Tab.1 Wind direction during measurement

表2 实测波浪要素值Tab.2 Wave parameter of measured values
3.2 实测波浪力的估算
围堰顶高程+7.9 m,底高程-4.4 m,海床面高程-9.9 m。其中围堰顺桥向长23 m,横桥向宽14.8 m。本次压强测点共24个,分三层布置,如图4所示。

4-a 正向布置 4-b 侧向布置图4 围堰压强测量点布置示意Fig.4 Layout sketch of pressure measurement point of cofferdam
根据围堰各测点同步压强实测值,在扣除各测点的静水压强后,通过与受力面积的乘积,得到作用在围堰上的波浪力。
P波=P测-P静
(18)
式中:P波为围堰所受的波浪压强;P测为实际测量的围堰总压强;P静为围堰所受静水压强,等于ρgh,其中,ρ为水体密度,g为重力加速度,h为相应测点处水深。
波浪力计算原则为波浪力=波动压强×受力面积,则围堰所受波浪力实测值如表3所示。
(19)
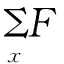

表3 SR40#围堰所受波浪力实测结果Tab.3 Measured values of wave force on SR40# cofferdam kN
4 波浪力特性研究与分析
4.1 波浪力模拟值特性分析
根据同期观测的波浪要素资料,采用本次研究建立的数学模型,对围堰波浪力进行计算。由于实测的波浪要素资料中缺少波向的相关内容,故计算中考虑了多种波浪入射角(分别为0°、11.3°、22.5°、33.8°、45°、67.5°、90°,角度为波浪入射方向与围堰长轴的夹角)的情况。
如图 5所示,当波浪以不同入射角作用于围堰时,围堰横桥向的波浪力呈现随入射角度增大而减小的变化规律,则顺桥向呈现随入射角度增大而增大的变化规律。同时顺桥向的波浪力最大值都大于横桥向的波浪力最大值,这是由于顺桥向在波浪垂直入射时的受力面积大于横桥向造成的。
4.2 波浪力模拟值与实测值对比及分析
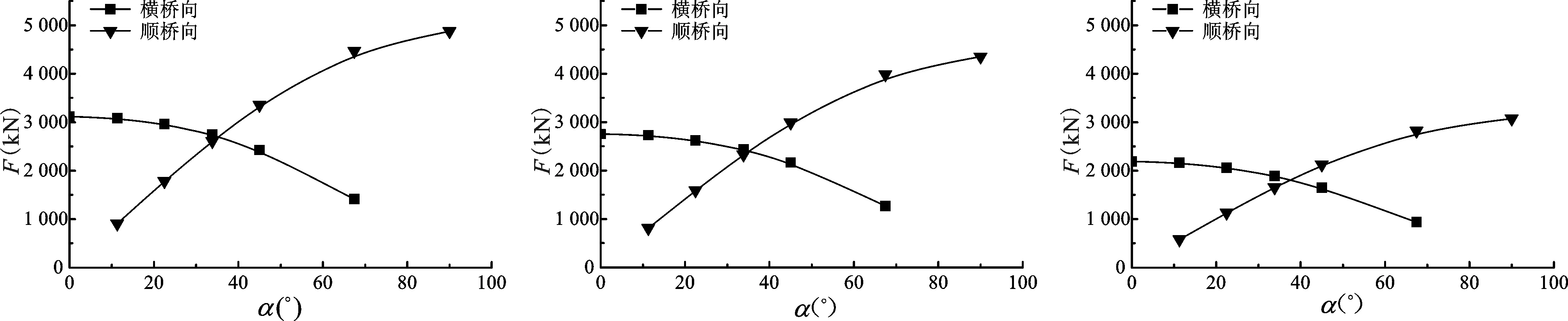
5-a 2015-09-29-00时刻 5-b 2015-09-29-01时刻 5-c 2015-09-29-02时刻
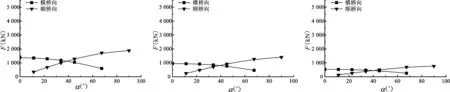
5-d 2015-09-29-03时刻 5-e 2015-09-29-04时刻 5-f 2015-09-29-05时刻

5-g 2015-09-29-06时刻 5-h 2015-09-29-07时刻 5-i 2015-09-29-08时刻图5 不同时刻变化波浪入射方向的横桥向与顺桥向波浪力Fig.5 Wave force of transverse and longitude of varied wave incident direction in different period

6-a 横桥向对比 6-b 顺桥向对比图6 波浪力模拟值与实测值的对比Fig.6 Comparison of wave force in simulating value and measuring value
如图6-a所示,横桥向模型计算值与实测值吻合较好的点大部分都在22.5°~67.5°之间。如图6-b所示,顺桥向模型计算值与实测值吻合较好的点大部分都在33.8°~90°之间。这可能是由测量时段大部分波浪入射方向集中在此角度范围内引起的。根据同期观测的风速资料显示,风向大致在27°~133°之间(与正北向夹角),假定波向与风向大致相同,据此推测,波浪入射方向大致在23°~90°之间,与计算吻合较好。这也从侧面验证了本次模型计算结果的正确性。但除横桥向2015-09-29-05(图中以“5”表示)时外,模型计算值与实测值符合较好。横桥向2015-09-29-05时计算值与实测值相差较大,这可能是由2015-09-29-05时测量的波浪要素偏小所致。顺桥向2015-09-29-06与2015-09-29-09(图中以“6”“9”表示)时外,模型计算值与实测值符合较好。顺桥向2015-09-29-06与2015-09-29-09时计算值与实测值相差较大,这可能是测量时仪器或者估算误差所致。
4.3 工程应用
平潭海峡公铁大桥起于长乐市松下镇,从松下港规划的山前作业区与牛头湾作业区之间入海,经人屿岛,跨越松下港区进港航道(即元洪航道)和鼓屿门水道,再依次通过长屿岛和小练岛、跨越大小练岛水道抵达大练岛,跨越北东口水道上平潭岛,大桥全长约16.338 km。
本次计算选取Z03主塔基础的承台结构进行波浪力计算,承台结构如图7所示,本次计算建立的承台三维数学模型及网格划分如图8所示。将计算结果与模型试验成果进行对比,对比结果表明本模型计算值与试验值符合较好。计算和试验采用的波浪要素,以及计算结果与试验值的对比情况如表4所示。

名称水深(m)波高H1%(m)有效波高Hs(m)平均周期(s)模拟值(kN)实测值(kN)Z03#主墩54.542.201.484.833833334
注:表中试验值引自文献[9],为承台结构所受的波浪力值,均通过波浪港池物理模型试验研究得到。
5 结论
本文采用源汇分布法即边界元法,基于波浪线性绕射理论,建立了大尺度结构基础波浪力计算的三维数学模型。经与圆形墩解析值以及平潭海峡公铁大桥围堰波浪力实测值对比表明,本模型对大尺度结构物波浪力计算具有较高的精度。由于跨海桥梁大尺度结构波浪力实测值的缺乏,以往模型验证均与模型试验值进行对比,本次模型首次与实测值进行了对比验证。鉴于本次验证的数据较为有限,且缺少波向的观测,建议下阶段继续加强对跨海桥梁基础波浪力的观测,进一步对模型进行验证。
参考文献:
[1]胡勇,雷丽萍,杨进先.跨海桥梁基础波浪(流)力计算问题探讨[J].水道港口,2012,33(2):101-105.
HU Y, LEI L P, YANG J X. Study of wave force on foundation of sea-crossing bridges[J].Journal of Waterway and Harbor, 2012,33(2):101-105.
[2]李玉成,滕斌. 波浪对海上建筑物的作用[M].北京:海洋出版社,2002.
[3]任效忠,王永学,王国玉.波浪对准椭圆沉箱作用的三维数值计算模型[C]//左其华,窦希萍. 第十四届中国海洋(岸)工程学术讨论会论文集.北京:海洋出版社,2009:594-599.
[4]张婷.波浪的三维数值模拟及其应用[D].天津:天津大学,2009.
[5]张婷,贺捷,黄锦林.海洋平台波浪荷载数值模拟研究[J].船海工程,2013,42(5):150-154.
ZHANG T, HE J, HUANG J L. Numerical Simulations of Wave Forces on the Offshore Platform[J].SHIP & OCEAN ENGINEERING, 2013,42(5):150-154.
[6]康啊真,祝兵,邢帆,等.超大型结构物受波浪力作用的数值模拟[J].工程力学,2014,31(8):108-115.
KANG A Z, ZHU B, XING F, et al. Numerical Simulation of Wave Forces on Very Large Structures[J]. Engineering Mechanics, 2014,31(8):108-115.
[7]Sarpkaya T, Isaacson M. Mechanics of wave forces on offshore structures, Offshore structures [M]. Van Nostrand Reinhold Company, New York,1981.
[8]Wehausen J V, Laitone E V. Surface waves. Handbuch der Physik[J]. Springer-Verlag, Berlin, 1960, 9: 446-778.
[9]王登婷,潘军宁.平潭大桥波浪力试验研究[R]. 南京:南京水利科学研究院,2013.
