某弹簧式灌水器流道的三维UDF动网格数值模拟
2018-05-10祁永斐
祁永斐,赵 涛
(1.新疆工程学院,乌鲁木齐 830052;2.新疆农业大学 水利与土木工程学院,乌鲁木齐 830052)
微灌技术具有省水、省工、节约生产成本以及对地形和土壤适应性强等优点,节水效果极其显著,是一种很有发展前途的节水灌溉方法[1]。灌水器在微灌系统有着广泛的应用,为了使微灌系统达到高效节水,灌水均匀的目的,对灌水器内部流道的优化及获得相关水力学参数有着重要的意义[2]。

图1 灌水器内部构造图Fig.1 Internal structure diagram of the emitter
近年来有越来越多的学者利用数值模拟的方法对灌水器进行设计和优化,这种方法可以弥补理论分析的局限,替代了高成本的试验研究[3-4]。有学者采用分步式CFD对压力补偿式灌水器进行数值计算,获得水力学参数的关系曲线[5];或者对不同压力下的补偿式灌水器,采用流固耦合的数值方法及可视化试验法[6]进行研究;通过选取不同的紊流模型从网格划分的角度对双向流流道计算,也可以得到流态指数对水力性能的影响[7]。通常对于灌水器内部流场运动的研究,主要采用假设边界位置不随时间变化的方法进行定常或非定常的计算,但在流量变化时,是无法准确描述流域边界运动引起流域形状随时间变化的状态。前人利用二维动态网格技术对类似的稳流器进行了初步的研究[8],本文针对弹簧式灌水器结合UDF程序进行三维的动态网格模拟;不仅减少了优化时间,也节约了设计成本。
本文中提到的灌水器,其工作原理是通过隔板位置的上下游移动来改变过流面积和流量(见图1),研究的过程是以隔板为研究对象,不同入口压力为计算条件,采用UDF和动网格方法对调节流道进行数值计算,从而实现对灌水器内部流道运动的模拟,并获得水头损失、压力与流量的关系。
1 CFD建模与计算
1.1 基本假设
根据建模和计算的需要,对该灌水器流道内水体流动应用CFD有限体积法进行模拟,并做如下假设[9-10]:常温,不可压缩粘性流体,非定常流动,忽略流体表面张力作用。
1.2 控制方程
为选取较理想的湍流模型,以运动隔板为研究对象,分别采用标准k-ε模型、RNGk-ε模型、Realizablek-ε模型和RSM模型对隔板在任意时刻,任意3个位置进行模拟计算,并对比实验值,结果见表1。

表1 四种模型模拟情况对比Tab.1 Four kinds of model simulation comparison
从表1中计算结果和计算时间的对比发现,对灌水器进行模拟计算采用标准k-ε模型较其它3种模型更合理,其基本控制方程和定解条件分别表示如下[11-12]
连续方程
∂uj/∂xj=0
(1)
动量方程
(2)
紊动能方程
(3)
紊动能耗散率方程
(4)
以上表达式中,i=1,2,3,即{xi=x,y,z},{ui=u,v,w};j为下标;常用模型参数为Cμ=0.09,Cε1=1.44,Cε2=1.92,σk=1.0,σk=1.3。
1.3 网格划分
目前在CFD的计算中,非结构化网格的应用非常广泛[13]。灌水器的内部流道几何空间是随压力变化的,除需要应用非定常的流体力学基本方程外,还要合理描述不断变化的几何空间。由于灌水器流道形式特殊,内部构件较多,本研究分别采用基本结构单元尺寸0.5 mm的六面体结构网格模型,基本结构单元尺寸0.5 mm的四面体非结构网格模型,以及上下游管道采用1 mm的结构网格结合局部细化0.4 mm的四面体网格的混合结构网格模型这3种情况来分别进行计算,计算结果对比见表2,综合考虑计算结果及收敛时间的精确性,选取局部细化处0.4 mm、边界规则处1 mm的混合结构网格模型,网格划分见图2。

图2 混合结构网格划分图Fig.2 Hybrid mesh structure diagram

类别结构网格模型非结构网格模型混合结构网格模型网格数目(万个)4.507.6010.07模拟值与实测值误差(%)30.1218.918.02计算收敛时间(h)1.81.451.0
1.4 动网格计算模型
很多双向流固耦合分析都会伴随大变形问题,固体部分的大变形一般不会导致网格错误,而流体区域的大变形则很容易导致网格错误,本研究采用标准的网格重构技术,即动网格技术可以很好地解决流场网格的变形问题[14]。动网格的生成途径主要有3种:动态分层方法、网格重构法、弹簧光顺模型[15],根据灌水器内部隔板的运动特点,本研究采用弹簧光顺模型和动态分层方法。
弹簧光顺模型需要设置弹性常数因子(Spring Constant Factor)、边界节点松弛(Boundary Node Relaxation)、收敛公差(Convergence Tolerance)、迭代数(Number of Iterations)等参数,弹性常数因子给出弹簧的阻尼,取值范围在0~1之间。边界节点松弛是针对边界节点的欠松弛,对于内部节点采用默认值1.0。收敛公差一般在求解节点位置采用,本文取0.001。根据计算时间迭代次数取20。
当选择动态层网格更新方法时,需要设置常数高度(Height Based)和常数变化率(Ratio Based),常数高度用于对网格层高度进行统一调整,而常数变化率用于有弯曲的区域,对于灌水器内部流道结构尺寸变化和常数高度值变化,需对分裂因子(Split Factor)和合并因子(Collapse Factor)进行设置,分别选取(0.2,0.02)(0.4,0.04)(0.8,0.08)三组参数对不同流量下灌水器进行模拟计算,根据收敛时间,计算误差最终确定分裂因子为0.4,表示旧的网格单元大于1.4倍网格时,新的一层网格生成,合并因子设置为0.04,意味着旧的网格单元小于0.8倍网格时,网格开始消失(表3)。
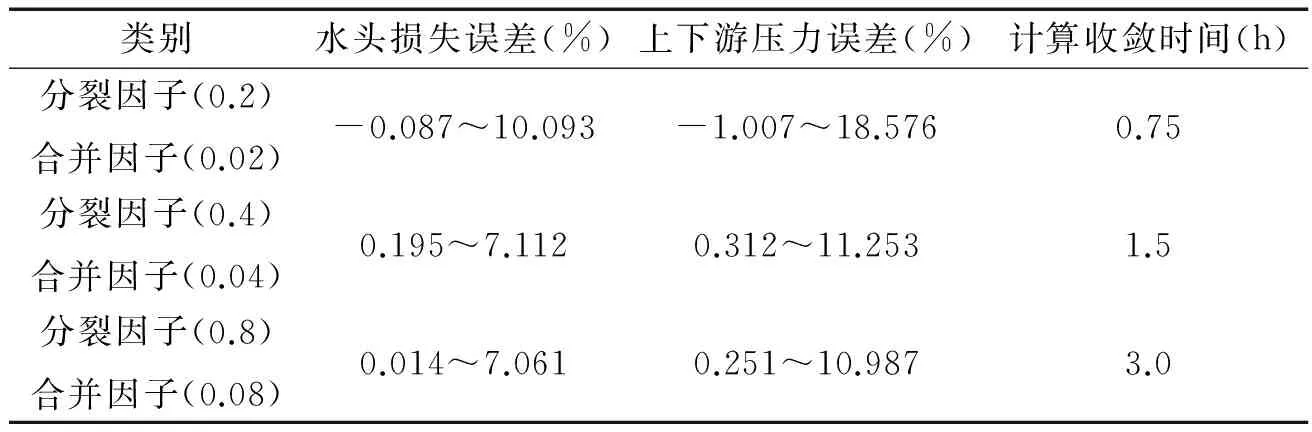
表3 参数设置计算结果Tab.3 Calculation result of parameter setting
1.5 UDF的编写及边界条件
灌水器分别采用速度进口和压力进口对比计算,分别编译在一段时间内速度达到1.2 m/s和压力达到300 Pa的UDF程序,出口设置为相对压力为0.010 MPa的压力边界条件,进行计算。根据计算结果(图3、图4、图5)可以看出采用速度进口时上下游压力略低于实测值,隔板位置靠近初始位置,而水头损失高于实测值,在大流量情况下,误差较大,综合比较压力进口和速度进口的计算误差以及计算时间(表4),本文选取压力进口进行计算。
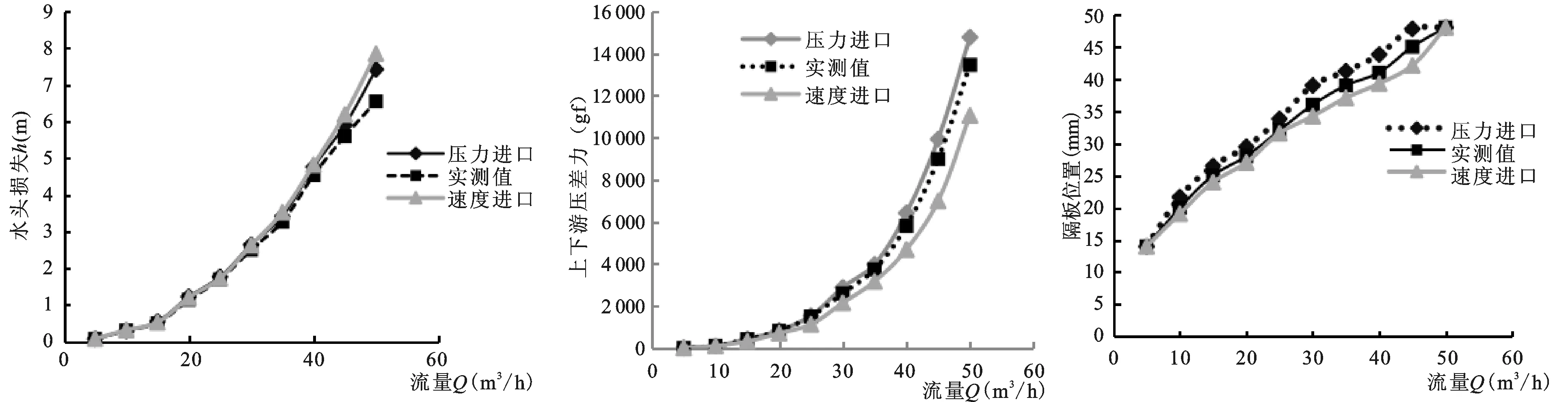

图3 水头损失对比图Fig.3Comparisonofheadloss图4 上下游压差力对比图Fig.4Comparisonofpressuredifferentialforce图5 隔板位置对比图Fig.5Comparisonofboardposition

表4 不同进口下计算误差Tab.4 Calculation error under different import
2 计算结果与分析
为了获得灌水器水头损失、上下游压力与流量的关系,根据物理试验及数值模拟计算结果,选取隔板在10组不同入口流量(5~50 m3/h)时的位置进行对比分析。
2.1 水头损失-流量关系
表5为灌水器水头损失与流量关系的数值模拟结果和实测结果二者之间的对比。水头损失的误差随着流量的增大而增大,在小流量时数值模拟值与物理试验值较为接近;数值计算时隔板的位置基本与实测值接近,浮动范围在9%以内,在小流量时,隔板位置更靠近起始位置。

表5 水头损失计算值与实测值对比Tab.5 Comparison between simulation result by head loss and measured data
2.2 上下游压差力-流量关系
表6为数值模型计算得到的上下游压差力的数据和实测数据的对比结果,随着流量的增大,上下游压差力也不断增大,最大误差在12%以内,隔板位置误差也不断增大,在小流量时,计算值与实测值吻合度较高;由于UDF程序设定隔板的最大位移为48 mm,所以当流量最大时,隔板不能继续运动,误差为0。
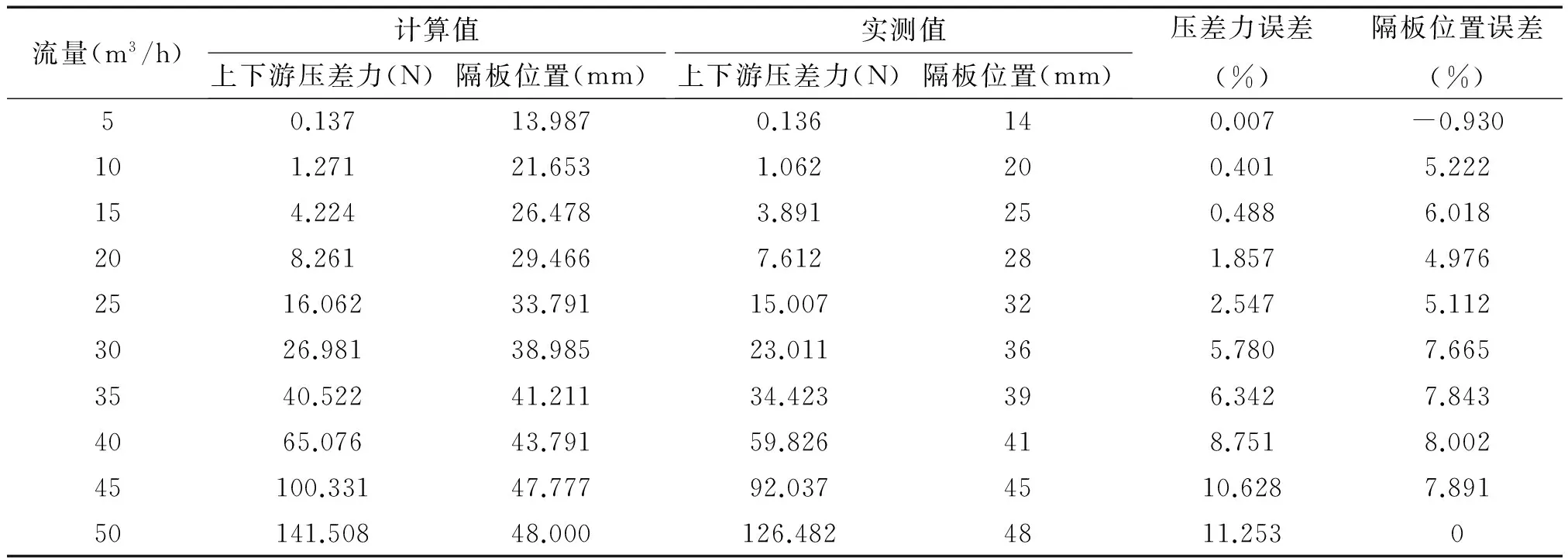
表6 上下游压差力计算值与实测值对比Tab.6 Comparison between simulation result by pressure differential force and measured data
2.3 模拟结果分析
(1)根据数值模拟情况,隔板位置随着入口压力的增大而向下游移动,水头损失增大,流道面积减小,降低过水能力;当流量减小,隔板位置向上游移动,水头损失减小,流道面积增大,提高了过水能力,如此循环使得灌溉系统在动态水压模式下,依然保证了稳定的出口流量,提高灌溉效率,减少灌水器的损失。
(2)进口流量增大时,隔板位置向下游移动,上下游压力增大;当流量减小,隔板位置向上游移动,上下游压力减小,隔板任意时刻的位置随进口压力的波动不断调节,使得灌水器内部流场连续产生波动效应,从而提高了低压运行或高压运行时的灌水均匀度,减小了流量波动对出口压力的影响。
2.4 误差分析
(1)经过数值计算结果与物理试验结果对比发现,水头损失和上下游压力在模拟大于40 m3/h流量时误差偏大,在12%左右,分析误差产生的原因主要是在进口压力的UDF程序编制上时间参数的设定,数值计算设定在一段时间内完成流量从5 m3/h到50 m3/h变化时隔板的运动情况,而由于试验手段的限制,物理试验只能测定在某种隔板固定位置不同流量下调节流道的水力参数,数模与物模存在一定的时间差异。
(2)隔板位置的误差在流量较大时达到8%,但波动不大,在小流量(25 m3/h以下)时实测值与计算值较为吻合,由于物理试验中根据理论计算预先设置好隔板的位置,隔板位置的确定和安置都存在一定的误差。
(3)物理模型试验存在一定的系统误差和偶然误差,包括试验仪器不够精确,取值计算上的误差等。
3 结论
(1)弹簧式灌水器的优势是通过内部结构的连续变化保持稳定的出流,因此灌水器的内部流道结构设计至关重要,并决定了灌水性能的优劣。本文通过数值模拟的方法对弹簧式灌水器内部流道进行了初步的研究,与物模结果的对比表明该方法是可行的。
(2)由于弹簧式灌水器内部流道的计算区域是动态变化的,因此本文采用动态网格技术进行数值模拟,实现了动态边界在水压力作用下运动过程的模拟,还结合内部弹簧的运动特点编制了UDF程序,整套计算方法除了可以为相似的微喷头、压力补偿器、流量调节器等具有运动边界情况的灌水器模拟计算提供参考外,还可用于灌水器的设计开发。
(3)模拟结果表明三维动网格的模拟结果与实验结果相比存在一定误差,因此需要进一步改进紊流模型并优化UDF的编写。
参考文献:
[1] 赵清水. 对微灌技术的点滴探讨[J]. 农业使用与维修,2010(1):100-101.
ZHAO Q S. Discussion of Drip Micro-irrigation Technology[J]. Farm Machinery Using & Maintenance, 2010(1):100-101.
[2] 罗良国,仁爱胜,王瑞梅. 中国农业可持续发展的水危机及广泛开展节水农业前景初探[J]. 节水灌溉,2000(5):6-10.
LUO L G,REN A S,WANG R M. An Elementary Study on Water Resource Crisis and Agricultural WS Foreground for Agriculture Sustainable Development in China[J]. Water Saving Irrigation,2000(5):6-10.
[3] 朱献文. 滴灌系统毛管流量调节器研制与开发[D].陕西:西北农林科技大学水建学院,2004:5-7.
[4] 聂磊,史玉升,魏青松,等. 基于灌水器流量的湍流模型适应性研究[J].节水灌溉,2008(1):13-17.
NIE L,SHI Y S,WEI Q S, et al. Research on Adaptability of Different Turbulent Models Based on Flow Discharge of the Drip Emitters[J]. Water Saving Irrigation,2008(1):13-17.
[5] 王周奇.浅谈双支管滴灌系统在果棉间作套种中的应用[J].南水北调与水利科技,2013(2):125-127.
WANG Z Q.Application of Two-branch-pipe Drip Irrigation System in Fruit-Cotton Intercropping[J]. South-to-North Water Transfers and Water Science & Technology,2013(2):125-127.
[6] 金文,张鸿雁,何文博.灌水器流道结构对水利性能影响的数值分析[J].中国农业大学学报,2012(17):139-143.
JIN W,ZHANG H Y,HE W B.Numerical Investigation on effect of Channel Structure to Hydraulic Performance of Emitter[J].Journal of China Agricultural University,2012(17):139-143.
[7]田济扬,白丹,于福亮,等.基于FLUENT软件的滴灌双向流流道灌水器水力性能数值模拟[J].农业工程学报,2014,30(20):65-71.
TIAN J Y,BAI D,YU F L, et al. Numerical Simulation of Hydraulic Performance on Bidirectional Flowchannel of Drip Irrigation Emitter Using Fluent[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014,30(20):65-71.
[8]聂境,赵涛. 齿形迷宫流道流场数值模拟与优化[J]. 节水灌溉,2011(7):40-42.
NIE J, ZHAO T. Numerical Simulation and Optimization of Tooth Shape Labyrinth Flow Channel[J]. Water Saving Irrigation,2011(7):40-42.
[9] 于勇,张俊明,姜连田. FLUENT入门与进阶教程[M]. 北京:北京理工大学出版社,2008:2.
[10] 孟桂祥,张鸣远,赵万华. 滴灌滴头内流场的数值模拟及流道优化设计[J]. 西安交通大学学报,2004(9):921-924.
MENG G X,ZHANG M Y,ZHAO W H. Numerical Flow Simulation and Optimum Channel Design of Drip Irrigation Emitter[J]. Journal of Xi′an Jiaotong University, 2004(9):921-924.
[11]李鹏飞,徐敏义,王飞飞.精通CFD工程仿真与案例实战[M].北京;人民邮电出版社,2011.
[12]朱红钧,林元华,谢龙汉. FLUENT流体分析及仿真实用教程[M]. 北京:人民邮电出版社,2010:2-3.
[13]李进良,李承曦,胡仁喜,等. 精通FLUENT6.3流场分析[M]. 北京:化学工业出版社,2010:2-3.
[14]江帆,黄鹏.FLUENT高级应用与实例分析[M].北京:清华大学出版社,2008.
[15]张凯,王瑞金,王刚. Fluent技术基础与应用实例[M]. 北京:清华大学出版社,2010:2-3.
[16]韩占忠,王敬,兰小平. FLUENT流体工程仿真计算实例与应用[M]. 北京:北京理工大学出版社,2004:19-20.
