基于不变集的半挂汽车列车防侧翻控制研究

欧 健，苏帅康，杨鄂川，王永胜

(重庆理工大学 a.车辆工程学院； b.机械工程学院， 重庆 400054)

半挂汽车列车往往具有载质量大、重心偏高、轮距相对于车身高度过窄等结构特点，在行驶的过程中遇到大幅度或急促的转向操作后车辆容易发生侧倾甚至导致侧翻。考虑到各种不确定性，例如驾驶员输入不确定性[1]、测量误差、参数估计以及半挂车高度的非线性带来的模型失配问题，提高控制器的鲁棒性变得十分必要。非线性MPC(model predictive control)需要求解复杂的非凸非线性规划问题,即使在变量较少的情况下,计算也相当复杂[2]，而应用不变集理论可以较好地解决这一问题。Mayne等[3-4]提出Tube不变集的概念，并将其应用到鲁棒预测控制器的设计中，计算出不确定性系统误差的不变集，通过收缩其状态与控制变量的约束集，进而保证不确定系统的鲁棒性。其对受干扰的离散系统进行了可达性分析，奠定了预测控制器处理扰动的设计基础。秦伟伟等[1]针对一类干扰有界约束，引入最小鲁棒正不变集,设计覆盖系统平衡面的相互重叠的多面体不变集序列,并以此结合Tube不变集方法,设计了基于不变集切换的鲁棒控制策略，通过应用到连续搅拌反应釜(CSTR)验证了控制效果。韦超毅[5]基于遗传算法和L-M优化算法相结合的辨识方法设计了LQR(linear quadratic regulator)控制器以决策出最优附加横摆力矩来控制半挂汽车列车的侧倾状态，但未考虑控制器的鲁棒性。

本文针对驾驶员行为不确定性、模型失配及半挂汽车列车的非线性特性等问题，将不变集理论引入半挂车侧翻控制器设计中，在控制器设计阶段将以上不确定性因素考虑为受约束于车辆状态的集值函数(set-valued function)。本文基于不变集理论，通过终端不变集约束处理鲁棒控制设计的不确定性问题；采用模型预测控制算法设计合理的目标函数，以期使车辆停留在状态稳定的区域，控制横向载荷转移率在0.7以内，达到防侧翻控制的目的。

1 半挂汽车列车动力学模型

简化的7自由度动力学模型包含牵引车的横摆、侧向和侧倾，挂车的横摆、侧向和侧倾及牵引车与挂车的铰接角7个自由度。

图1 7自由度动力学模型

由一般运动方程和受力分析，建立牵引车的数学模型如下：

1) 牵引车侧向动力学方程:

(1)

2) 牵引车侧倾动力学方程：

m1sgh1sinφ1-F4h1ccosφ1+Mf1+Mr1

(2)

3) 牵引车横摆动力学方程：

(3)

由一般运动方程和受力分析，建立挂车的数学模型如下：

1) 挂车侧向动力学方程：

(4)

2) 挂车侧倾动力学方程：

F4h2ccosφ2+M2

(5)

3) 挂车横摆动力学方程：

(6)

4) 牵引车与半挂车在牵引销连接处的约束方程：

(7)

应用线性轮胎模型[6]可知，侧向力Fi(i=1,2,3)与侧偏角成比例关系：

(8)

将以上方程整理为状态空间形式：

(9)

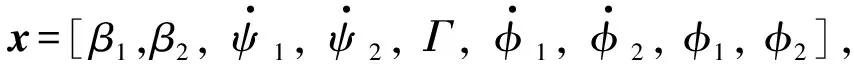
考虑到所建立的模型与实际车辆存在不匹配、半挂车的高度非线性及液压系统的迟滞等因素，引入附加不确定性因数wu得到修正后的7自由度车辆模型：

(10)

不确定性因素会导致模型的不匹配，将这种不匹配描述为模型中矩阵A、B参数的扰动，采用Matlab函数c2d对模型进行离散化，采样时间设置为0.05 s，离散化后的车辆模型为

(11)

其中：Ad=[Ad(:,1),Ad(:,2)+G*Bd(:,1)];G为稳态横摆角速度增益，取值为0.5；Bd={0.9*LBd,LBd,1.1*LBd}。

将驾驶员转角不确定性考虑为附加干扰：

E=Bd(:,1)

Bd(:,1)={δd:|δd-Gψ′|≤ε, |δd|≤δd, max,ε>0}

2 鲁棒预测模型控制器设计

应用鲁棒模型预测控制理论，针对半挂汽车列车的强非线性和所建立系统的不确定性，设计具有一定鲁棒性的侧倾稳定性控制器。根据系统的状态预测出下一时步的状态，并计算出一组最优控制输入(即防侧翻力矩)，以保持车辆的横向载荷转移率在安全范围之内，减小侧翻危险的发生。侧翻稳定性控制框图见图2。

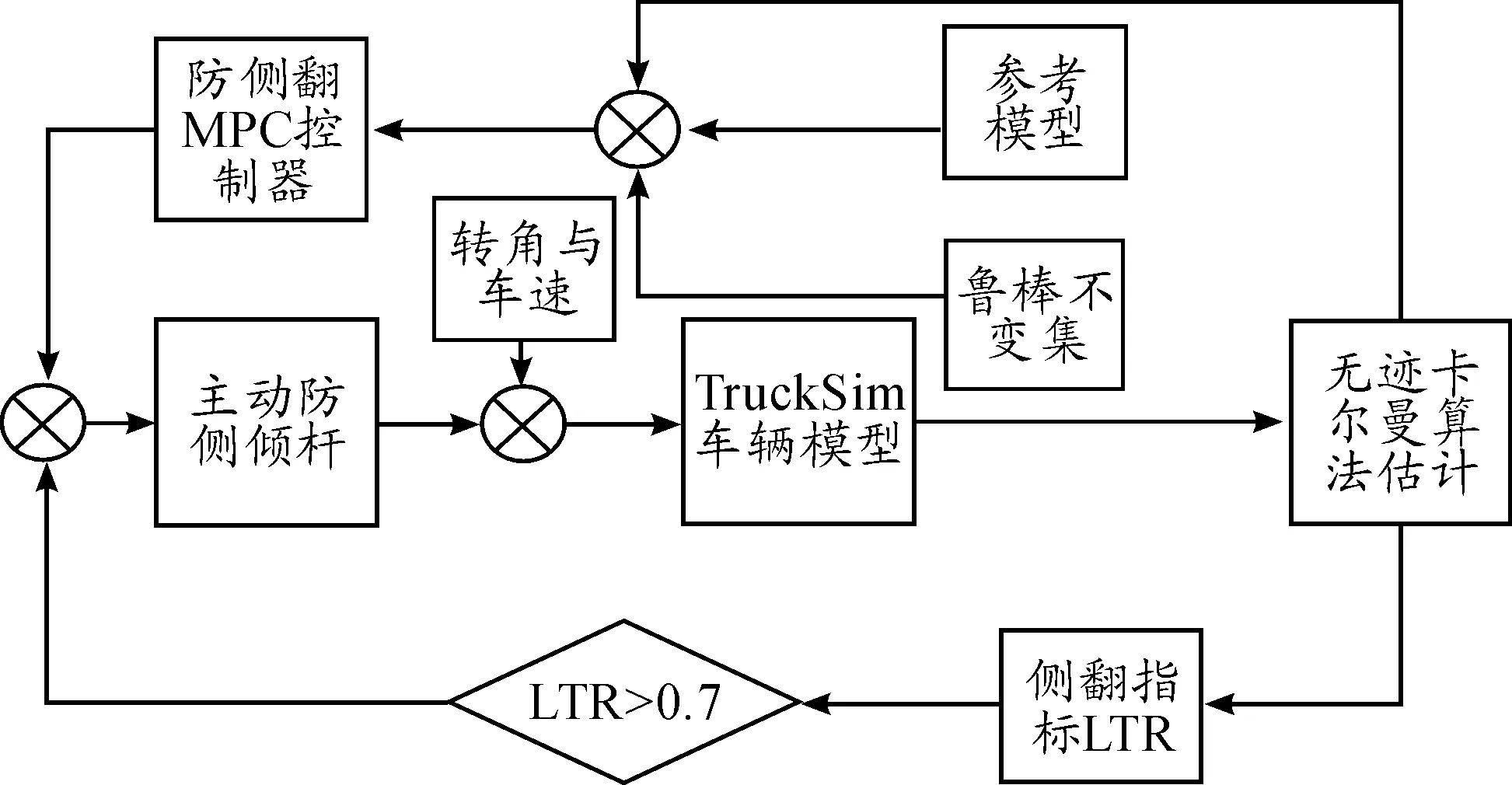
图2 侧翻稳定性控制框图

2.1 鲁棒控制不变集RCI的计算

将状态、控制输入和随机扰动量的硬约束考虑为全局约束，对目标状态进行鲁棒控制不变集计算作为控制器的终端约束，离线求解最优控制率以减少计算量。

鲁棒控制不变集是针对可控输入的系统，如果状态集在鲁棒控制不变集内，则总存在一个控制器能够遵循系统约束。计算最大鲁棒控制不变集C∞的算法见表1[7-8]。

表1 最大鲁棒控制不变集算法

不变集的求解计算基于Matlab中MPT3.0工具箱[9]。由于RCI中包含的变量是高维度的，无法直接用图形表述，故选取前3列的三维投影来描述，如图3所示。

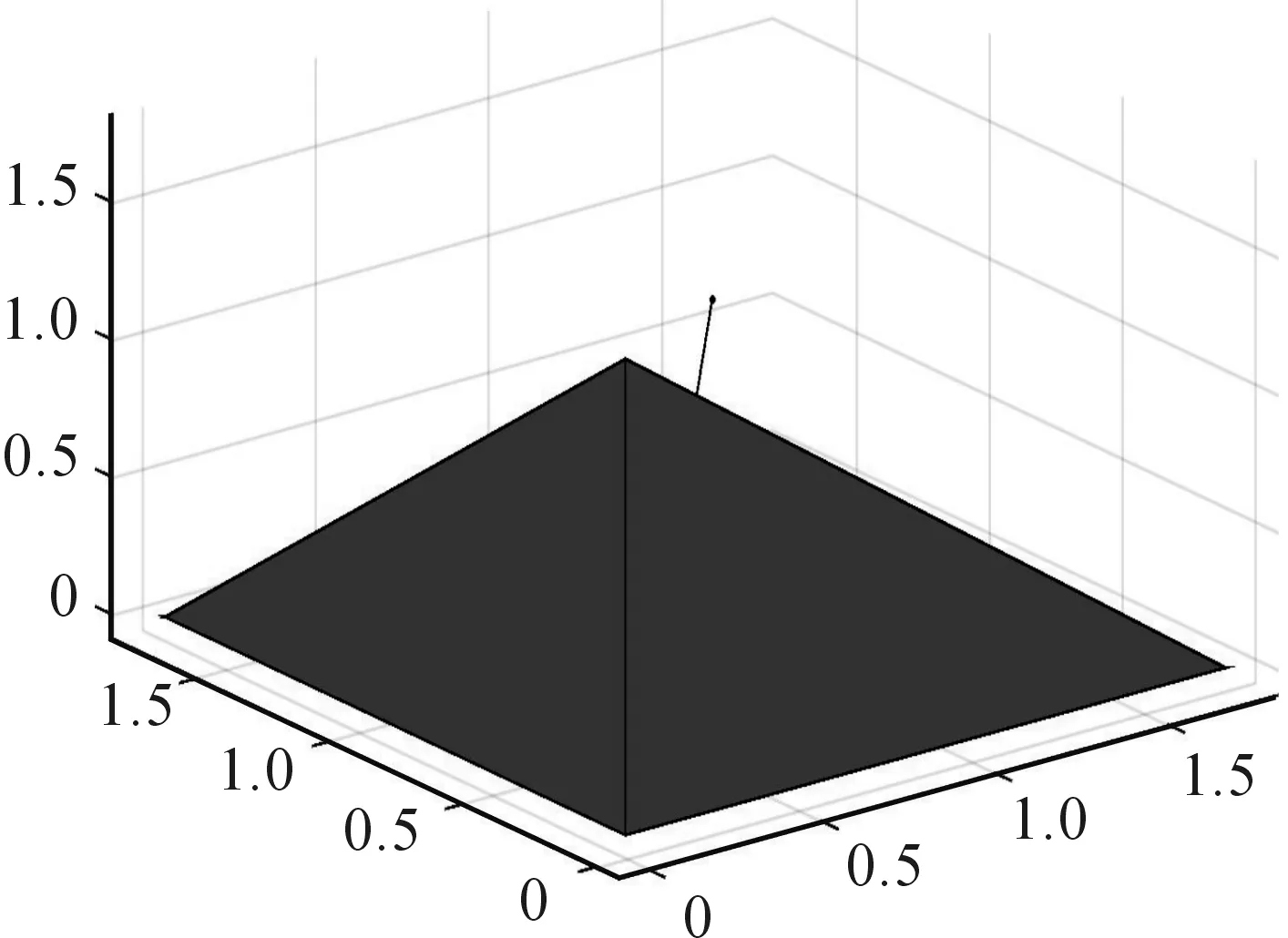
图3 RCI前三列的三维投影图

2.2 鲁棒模型预测控制器设计

将离线计算好的鲁棒控制不变集通过Matlab中MPT3.0工具箱[9]调用，加载至控制器。采用在线的模型预测控制器，针对模型中包含的不确定性，跟踪参考模型给出的状态，滚动求解带约束的有限时域最优控制问题， 得出最优防侧翻力矩，以控制车辆状态避免侧翻危险。

模型预测控制可以在设计反馈控制律时直接考虑输入与输出约束，因而被广泛运用。MPC反馈控制律基于计算的最优控制输入指令，通过求解以下形式的最优化问题获得[10]：

(12)

s.t.xk+1=f(xk,uk,wk)

(13)

xk∈χ

(14)

uk∈u

(15)

wk∈w

(16)

xN∈T

(17)

x0=x(t)

(18)

式中：xk、uk、wk是在第k时步预测的状态、控制输入和干扰；预测的初始值x(t)是被控对象当前量测(或估计)的状态；x、u分别为状态、输入约束；w为附加干扰约束；T为终端集。预测时域为N，目标函数为J。最优化的运行与u0,…,uN-1相关，仅将其中的第1项u0用于被控对象。

目标函数为

式中：Q、R和QN均为正定矩阵；xN为终端状态量。

把半挂车的主动防侧翻控制问题看作一个标准MPC问题来解决，在每一个采样步长通过解算带约束的有限时间最优控制问题计算最优输入控制序列，并在下一时步根据新的车辆状态解算最优控制问题。设计相关目标函数计算最优控制输入为：

u*=[Mf1,Mr1,Mf2]

式中：Mf1为牵引车转向轴的主动防侧翻力矩；Mr1为牵引车驱动轴的主动防侧翻力矩；Mf2为挂车集中质量轴的主动防侧翻力矩。

3 典型工况的仿真验证

为验证所设计的控制器的防侧翻效果，选取双移线和角阶跃两种典型工况进行仿真验证，建立Simulink-Trucksim联合仿真模型。在未控状态和受控状态、MPC控制和TTR控制状态下分别进行仿真，之后通过对比验证得出鲁棒模型预测控制器的控制效果。

3.1 双移线工况

车速设置为80 km/h，路面附着系数为0.3，冰雪路面。牵引车和挂车的各个状态量见图4。

图4 双移线工况下主动控制和不控制的车辆状态量对比

在双移线工况下，在6.42 s时的未控状态下，牵引车与挂车的LTR均达到1，且侧向加速度发散。通过仿真发现车辆已发生侧翻，故此后的数据丢失。在MPC控制器的控制下可以看到：车辆状态稳定，有效避免了侧翻危险。所需的防侧翻力矩牵引车驱动轴为最大，其次是转向轴和挂车集中质量轴，因此在加装主动防侧倾杆时可选择规格较大的牵引车驱动轴，另外两轴可选择相对较小的牵引车驱动轴以节约成本。

3.2 角阶跃工况

车速设置为100 km/h，路面附着系数为0.85，良好路面。牵引车和挂车的各个状态量见图5。

采用角阶跃工况模拟实际行驶过程中的驾驶员突然转向行为，由仿真结果可知：在未控状态下，半挂车在5.2 s时刻侧倾角趋于无限大，车辆发生侧翻；而经主动控制后，半挂车辆的横向载荷转移率、侧倾角、侧向加速度均可收敛并处于安全区域内，所设计的控制器可以较好地避免侧翻危险。

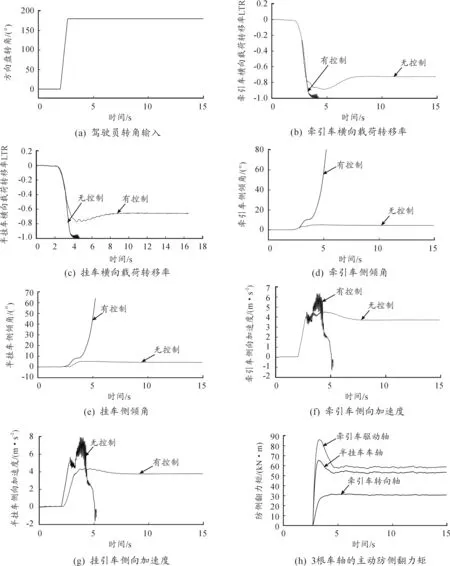
图5 角阶跃工况下主动控制和不控制的车辆状态量对比

4 结束语

本文将不变集的概念引入半挂汽车列车的防侧翻控制器设计中，应用鲁棒模型预测控制理论，增强了控制器对模型失配，以及半挂车高度非线性所带来的不确定性干扰的鲁棒性，并进行了典型试验工况仿真。半挂汽车列车在控制器施加主动防侧翻力矩后，较之未控状态下的侧倾状态有明显改善，施加控制后横向载荷转移率从1变为0.7以下，侧倾角和侧向加速度等表征侧倾状态的指标也由超出侧翻阈值的危险值减小至安全区域内，且曲线得到收敛不再发散，验证了所设计模型预测控制器的良好防侧翻性和鲁棒性。本文为半挂车的防侧翻研究提供了理论支持，但在极限工况下，车辆仍容易失稳，因此在进一步研究中可考虑加入预警系统，提醒驾驶员及时降低车速和减小方向盘转角，以实现最大程度上的主动安全。

参考文献：

[1] CARVALHO A,PALMIERI G,TSENG H E,et al.Robust vehicle stability control with an uncertain driver model[C]//2013 European Control Conference.Switzerland ：IEEE,2013:440-445.

[2] 秦伟伟,马建军,刘刚,等.一类干扰有界约束非线性系统的鲁棒模型预测控制[J].控制理论与应用,2011,28(5):709-714.

[3] MAYNE D Q，SERON M M，RAKOVIC S V．Robust model predictive control of constrained linear systems[J]．Automatica，2005，41(2)：219-224.

[4] RAKOVIC S V，KERRIGAN D，MAYNE D Q，et al．Reachability analysis of discrete-time systems with disturbances[J]．IEEE Transactions On Automatic control，2006，51(4)：546-561.

[5] 梁群彰.基于参数辨识的列车侧翻控制系统的研究[D].南宁:广西大学,2016.

[6] 于志新.基于MPC的重型半挂车动力学稳定性多目标控制研究[D].长春:吉林大学,2015.

[7] PALMIERI G，BARIC M，GLIELMO L，et al．Robust vehicle lateral stabilization via set-based methods for uncertain piecewise affine systems：Experimental results[C]//Decision and Control and European Control Conference．USA:IEEE，2011：3252-3257.

[8] BORRELLI F，BEMPORAD A，MORARI M．Predictive control for linear and hybrid systems；Inpreparation[EB/OL]．[2017-12-20].http://www.mpc.berkeley.edu/mpc-course-material.

[9] HERCEG M， KVASNICA M， JONES C N，et al．Multi-parametric toolbox 3.0[C]//Control Conference．USA:IEEE，2013：502-510.