基于数据挖掘的白酒分类问题研究

2018-05-10刘亚清马艺翔

中国酿造 2018年4期

刘亚清,马艺翔

(北方工业大学经济管理学院,北京 100144)

白酒是一种以粮谷为主要原料,由淀粉或糖质原料制成酒醅或发酵后经蒸馏而得的饮品,在我国具有悠久的历史。不同品质白酒的市场需求存在较大差异,因此各白酒生产商都力求生产出高品质白酒以获取更高利润。但是由于酿造过程的不确定性较多,同一批次酿造的白酒品质也能存在较大差异。基于白酒成分中的相关因素进行分析,量化各因子对于白酒品质的影响作用,从而达到对白酒品质进行初步分类的目的；另一方面,随着统计方法的迅速发展以及计算机运算能力的提升,基于样本信息的数据挖掘模型,能够有效降低人为主观意识带来的偏误。因此,基于数据挖掘方法对白酒品质进行分类研究,具有很好的研究价值和现实指导意义。

在企业生产中,对于白酒分类问题的研究多应用感官评定和气相色谱法进行分类,但感官评定法容易受到主观和客观的条件影响,结果不够理想［1］。因此,最近几年的相关研究多基于不同的白酒实验数据,通过构建不同的模型对白酒分类问题进行客观分析。李建等［2］基于纯粮白酒在碱性加热条件下在波长363 nm处存在吸光度值差异的原理,指出可以通过纯粮白酒标准曲线来确定该酒样中纯粮白酒的比例；杨建磊等［3］基于最小二乘支持向量机方法,对近百种白酒的荧光光谱进行分析,指出光谱中波峰个数、主波峰位置和最佳激发波长贡献率最高,利用其进行分类能达到较为理想的效果；徐瑞煜等［4］则进一步利用主成分分析的方法对三维荧光光谱数据进行降维,进而利用支持向量机的方法对几种浓香型白酒进行鉴别；吕海棠等［5］利用红外光谱法,指出白酒分类可以基于白酒干燥物的指纹特征,不同种类下存在较大差异；王海燕等［6］利用压缩感知理论对白酒香型进行分类,指出该理论相比最小冗余误差方法能够提高识别率；彭祖成等［7］则选择白酒中的酯类、醇类等成分含量作为特征变量,构建聚类算法进行白酒分类,而王旭亮［8］则基于理化指标对中国名特白酒系统聚类分析；徐增伟等［9］通过构造神经网络模型研究大曲理化指标与白酒品质之间的联系；陈秀丽等［10］结合主成分分析法,用所建立的电子鼻系统对白酒进行了分类识别,发现准确率较高,田婷等［11］也指出主成分分析在处理电子鼻传感器响应信号时,对不同轮次酱香型白酒的区分效果要优于判别因子分析。赵金松等［12］则基于原子力显微镜技术,指出真假酒之间在微观形态上存在较大差异,可以由此进行真假鉴别。

从现有文献可以看出,对于白酒分类问题的研究,多集中于借助定量分析模型进行划分,能够客观给出白酒分类的指导方法。但是,当前的研究大多基于不同的实验指标数据,对白酒类型进行划分,但并未对相关指标对于白酒类型的具体影响力大小以及作用机理进行综合分析,且选取变量较多时容易产生信息冗余及多重共线性问题。因此,本研究通过选取相关特征变量,进而提取公共因子并结合现有研究对主因子进行分析定义,进行利用多分类Logistics模型对白酒品质进行分类回归,计算模型预测准确率,并确定各主因子对于白酒品质的影响力大小。

1 理论基础及变量选取

1.1 因子分析

作为一种常用的降维方法,因子分析通过研究众多变量之间的内部依赖关系,提取公共因子,用以表示原有数据的基本结构,并且利用这些公共因子表示变量的主要信息,由于这些假想变量是不可观测的潜在变量,故称为因子。

在进行因子分析时,首先对数据进行标准化处理,然后估计因子载荷矩阵,具体公式：

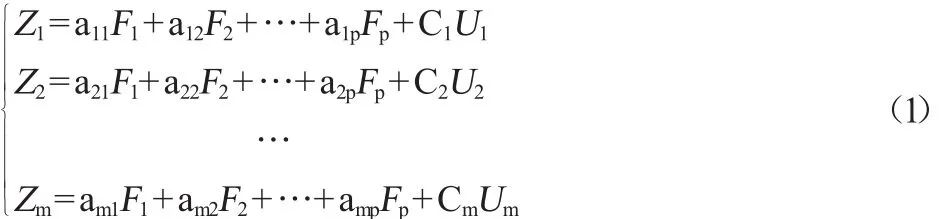
式中：Z1、Z2、…Zm为原始变量；F1、F2、…Fp为公共因子；a11、a12、…amp为不同因子在原始变量中所在的权重；U1、U2、…Um为各原始变量中除公共因子外自身所特有的特殊因子；C1、C2、…Cm为特殊因子在原始变量中所占的权重；表示为矩阵形式：

式中：A为因子载荷矩阵,一般采用主成分法进行估计,随后对A进行正交变换,从而对因子的意义进行解释。最后,通过因子得分函数,可以计算原有的每个解释变量在每个公共因子上的得分,从而对公共因子进行衡量。

1.2 多元logistics回归

多元logistics回归模型首先定义因变量某一水平作为基底,然后构建与其他水平的比值,建立“水平数-1”个广义logistics模型。以3水平因变量为例,其取值水平分别为1、2、3,回归模型构建如下：

显然,同时应当有p1+p2+p3=1,根据样本观测值进行参数估计后,计算出

通过对样本数据进行代入,可以分别计算该样本点被划分到这三类中的概率大小,通过数字比较,可以判断出该样本被划分到的类别,从而利用模型进行分类预测。

考虑到研究的问题以及数据的易得性,本实验选取加州大学欧文分校(University of California,UCI)数据库中的白酒品质数据集进行数据挖掘,该数据集的解释变量为通过物理化学测试得到的一些特征指标,具体指标包括非挥发性酸、挥发性酸、柠檬酸、残糖、氯化物、游离二氧化硫、总二氧化硫、密度、酸性、硫酸盐、酒精度,分别定义为X1～X11；被解释变量为白酒的品质分类,通过专家打分法得到,从最低的1到最高10共分为10类。考虑到样本集中各个品类白酒的样本量,本实验选择包含5、6、7这3个品级的白酒数据,其中等级5的白酒样本数有1 407个,占32.1%；等级6的样本数为2 148个,占49%；等级7的样本数为830,占18.9%。

2 实证研究

2.1 因子分析

由于该数据集中解释变量较多,并且其中部分变量明显具有相关关系,故构建相关系数矩阵,分析各变量之间的相关关系,具体结果如表1所示。

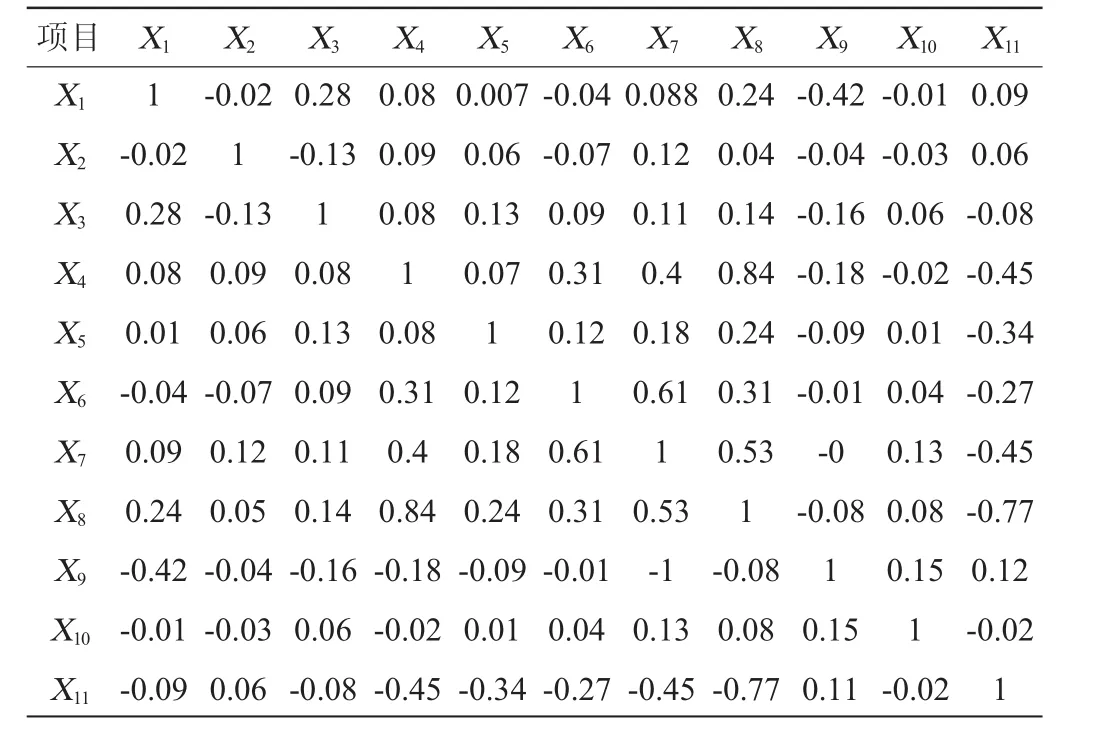
表1 相关系数矩阵Table 1 Matrix of correlation coefficients

由表1可知,X1与X3的相关性达到0.28,与X9的相关性达到-0.42,这是因为柠檬酸属于非挥发性酸中的一种,故两者关联度较高；X6与X7相关性达到0.61,因为游离二氧化硫是由总二氧化硫电解得到,因此具有较强的相关性；而X11酒精度与其他变量的相关性程度更高,这与其计算公式有关。

通过相关系数矩阵可以看出,各变量相关程度较高,直接进行回归容易受到多重共线性的影响,影响系数的准确程度,因此借助因子分析方法对原始数据集进行处理。使用该方法可以在变量中找出隐藏的具有代表性的因子,达到降维的目的,同时消除多重共线性问题。利用SPSS软件进行因子分析,最终得到4个公共因子,其中因子解释度结果如表2所示。

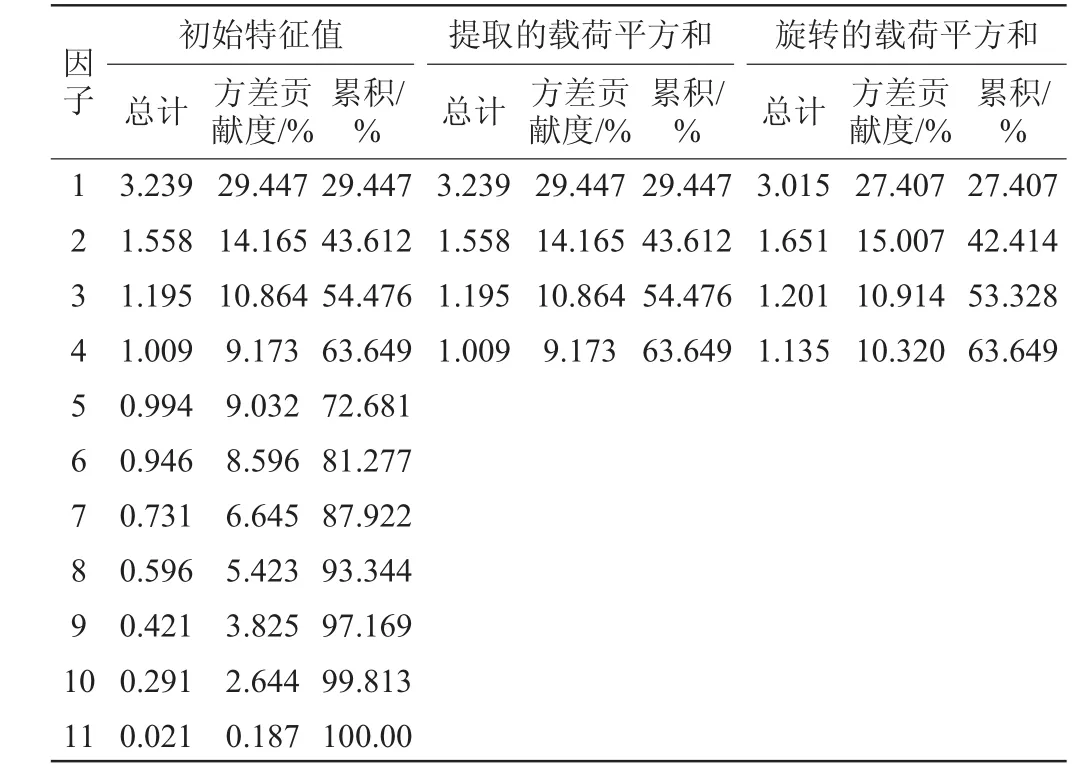
表2 因子解释度结果Table 2 Results of factor interpretation

由表2可知,模型从11个特征变量中提取出来4个主要的公共因子,其中因子1的方差贡献度为29.447%,前4个公共因子的解释度达到63.649%,说明这4个公共因子对于样本数据的提取程度较高,能够较好的代替相关特征变量进行解释说明。

根据成分得分系数矩阵可以得到每个公共因子的计算公式,根据分析结果,具体表达式如表3所示。

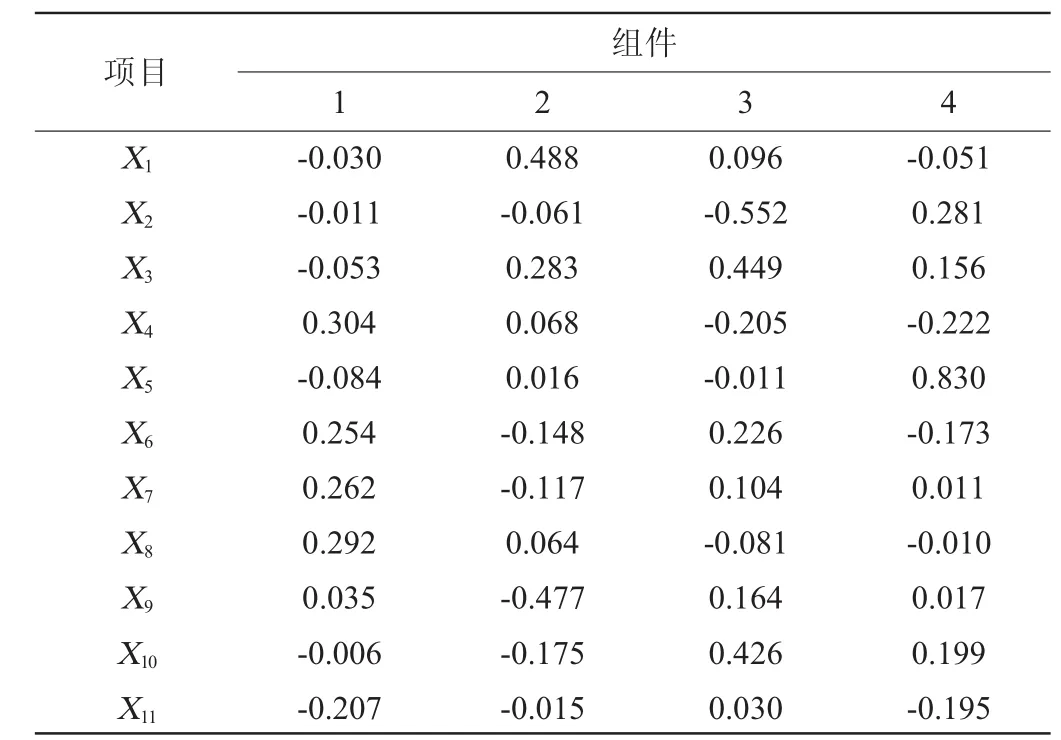
表3 成分得分系数矩阵Table 3 Coefficient matrix of component score

由表3可知,因子1中X4、X6、X7、X8的系数绝对值较大,均＞0.25,因此该因子的主要成分是残糖、游离二氧化硫、总二氧化硫、密度,有学者的研究表明［13］,在酒类的酿造过程中,酒精度越高,乙醛和葡萄糖越多,被结合的二氧化硫就越多,则游离的二氧化硫就越少,结合残糖因素,故因子1可以命名为甜味因子；因子2中X1、X3、X9的系数绝对值＞0.28,因此该因子中非挥发性酸、酸性、柠檬酸所占权重较大,有学者研究发现,白酒中的非挥发性酸包含乳酸、柠檬酸等,具有斧正口味,提高白酒质量的作用［14］,因此因子2可以命名为口味因子；因子3中X2的系数绝对值达0.552,因此该因子中挥发性酸的权重较大,由于白酒中挥发性酸是白酒中主要的呈味物质,故将因子3命名为香味因子；因子4中X5的系数达0.830,氯化物权重最大,有学者的研究表明［15］,白酒中的氯化物浓度较高,说明酒中的杂质较多,容易影响产品质量,故命名因子4为杂质因子；分别用I1～I4表示这4个公共因子。

2.2 参数估计

基于样本数据集,首先进行因子分析处理,保存处理后的各因子成分数据。并在3种品类白酒数据中各预留50个样本用于模型最后的预测检验,对于剩余的样本数据进行logistics回归,得到如下分析结果：

根据检验结果,各系数均通过1%显著性检验水平,参数估计准确度较高,利用该参数对预留的150个样本数据进行计算处理,得到不同因子水平下,该样本点被分类到这3种品类白酒的概率大小,具体结果如表4所示。

表4 白酒分类结果Table 4 Classification results of B aijiu

由表4可知,预留样本中,对于品类6的白酒预测准确度最高,准确率达90%；其次是品类5的白酒,准确率为48%；而对于品类7的白酒预测准确度最低,为8%。综合来看,样本点总体预测准确率为48.7%,而对于品类5与品类6白酒的综合预测准确率为69%。分析其原因,可能是由于样本数量的原因,在样本集中,品类5的数据占32.1%,品类6占48.5%,品类7白酒占19.4%。

为了分析各分类变量样本点数量的不同是否影响预测结果,同时考虑进行回归时样本量的充足性,在进一步的研究中,本实验选取各自选取了1 408个品类5和品类6的白酒样本集,对数据首先进行因子分析,进而采取二元Logistics回归分类,其模型回归结果准确率如表5所示。

表5 回归准确率结果Table 5 Results of regression accuracy

由表5可知,在样本数量相同时,对于品类5和品类6的白酒分类预测正确率,均维持在65%左右,整体预测正确率达到65.5%,相比较三分类模型,前两种品类白酒的综合预测准确率并未发生明显变化,但是对于单项预测的准确度有较大改变。因此,可以看出各分类变量样本集数据数目的大小,能够影响单个类别的预测准确度,但是对于综合准确度影响不大。

2.3 模型分析

由Logistics回归模型公式可以看出,随着白酒品类的提高,因子1、因子2和因子4的系数均在不断下降,而因子3的系数相应提高,说明因子1、2、4的提高对于白酒品质起负向作用,而因子3的减少能够提高白酒品质。分别针对各因子所含内容进行分析,在因子1的权重中,除酒精度的权数为负外,残糖、总二氧化硫、游离二氧化硫、密度的系数均为正,说明除酒精度对白酒品质的提升起正向作用外,其余因素起负向作用。而二氧化硫的含量偏低,说明白酒中的醛类含量较高,这是因为二氧化硫主要与乙醛结合的缘故,被结合就越多,则游离的二氧化硫就越少,乙醛在白酒贮存老熟过程中含量不断增加,能够赋予白酒的清香以及柔和感［16］,故其含量的提高能够促进白酒品质的提升；因子2中除酸性的权重为正外,非挥发性酸和柠檬酸权重均为负,又由于因子2的降低能够提高白酒的品质,说明非挥发性酸和柠檬酸能够提升白酒香气,而这与白酒中的不挥发酸具有斧正和稳定香气,提高酒体的总酸度等因素有关,能够丰富白酒香味。因子3中主要是挥发性酸的影响因素较大,且其权重为负,说明挥发性酸含量的提高能够提升白酒的品质,白酒中酸类组分是比较重要的呈味物质,也是形成白酒口味的主要香味成分和生成酯类的前驱物质,故品质较高的白酒中挥发性酸的含量也较高。

针对因子4,其主要影响因素时氯化物的含量,而氯化物的来源,主要是白酒酿造过程中的用水。同时,水的硬度体现在水中存在钙、镁等金属盐杂质的缘故,水的硬度过高将会导致成品白酒产生浑浊、失光的重要原因,影响白酒的品质。从Logistics回归结果也可以看出,随着白酒分类概率的提升,因子4的参数逐渐降低,因此氯化物含量的提高将会降低白酒品质。

3 结论

本实验通过收集关于白酒品质的相关数据,在对11个样本指标进行相关性分析时,发现变量间存在较为严重的多重共线性,故采用因子分析的方法,提取出4个主要公共因子,进而通过构造三分类变量的Logistics分类模型,进行参数估计,得到样本参数方程,并对预留的150个样本数据进行预测,发现对品类6白酒的预测准确度最高,而对品类7白酒的预测准确度较低。在对影响白酒品类的因素分析时,发现挥发性酸类物质对于白酒口感的提高具有促进作用,而酿造用水中氯化物成分会降低白酒口感。因此厂家在酿造白酒时,应当改进生产工艺,使得白酒中相关促进性因素能够得到提升,同时注重酿酒用水的来源,避免水中含有过多杂质,影响白酒品质。

参考文献：

［1］陈飞,张良,霍丹群,等.浓香型白酒基酒的现状和发展趋势［J］.中国酿造,2017,36(10)：5-8.

［2］李建,姜雪.浓香型纯粮白酒鉴别方法的研究［J］.中国酿造,2015,34(1)：118-121.

［3］杨建磊,朱拓,徐岩,等.基于最小二乘支持向量机算法的三维荧光光谱技术在中国白酒分类中的应用［J］.光谱学与光谱分析,2010,30(1)：243-246.

［4］徐瑞煜,朱焯炜,胡扬俊,等.三维荧光光谱结合PAC-SVM对几种浓香型白酒的鉴别［J］.光谱学与光谱分析,2016,36(4)：1021-1026.

［5］吕海棠,任彦蓉,李春花.红外光谱技术对浓香型和清香型白酒的品质分析［J］.中国酿造,2010,29(10)：175-177.

［6］王海燕,王虎,王国祥,等.基于压缩感知的白酒香型分类［J］.计算机工程,2015,41(3)：172-176.

［7］彭祖成,潘春跃.聚类分析在白酒质量和风味辨识的应用［J］.食品工业,2015,36(6)：250-252.

［8］王旭亮.基于理化指标对中国名特白酒系统聚类分析［J］.酿酒科技,2013(7)：5-8.

［9］徐增伟,曾黄麟,陶雪容.基于粗神经网络的大曲理化指标对白酒质量和产量影响分析［J］.中国酿造,2011,30(11)：101-103.

［10］陈秀丽,高海荣,黄振旭,等.电子鼻分析方法在白酒分类识别中的应用［J］.信阳师范学院学报,2014,26(7)：386-393.

［11］田婷,邱树毅,文聆吉,等.电子鼻技术对不同轮次酱香型白酒的区分与识别［J］.中国酿造,2017,36(10)：71-75.