船舶纵倾优化减阻数值模拟研究❋

童 骏, 涂海文, 孙江龙，2，3

(1. 华中科技大学船舶与海洋工程学院，湖北 武汉430074；2. 船舶与海洋工程水动力湖北省重点实验室，湖北 武汉 430074；3. 高新船舶与深海开发装备协同创新中心，上海 200240)

随着我国的能源需求越来越大，能源形势越来越严峻。在全球经济不景气的情况下，各大班轮公司也开始精耕细作，积极寻找降低运营成本的方法。液化石油气(Liquefied petroleum gas.简称LPG)船主要运输以丙烷和丁烷为主要成份的石油碳氢化合物或两者混合气,包括丙烯和丁烯,还有一些化工产品。液化气船因其特殊用途而产生了各方面的特殊要求,其技术难度大,代表当今世界的造船技术水平,造价为同吨位常规运输船的2～3倍,是一种高技术、高附加值的船舶，在我国巨大的能源需求需求下，LPG船舶具有更广阔的市场需求。

通过调整船舶的纵倾，在船舶某些特定航态下能够减小船舶阻力。国内早在1985年，王维宇[1]等总结了纵倾船舶的稳性计算方法提出了大倾角稳性和初稳性的计算表达式。邵世明[2]等对参数不同的高速排水型艇的初始纵倾对阻力影响进行了研究，发现对于高速排水型艇，适当尾倾可以得到减阻收益。邱斌彬[3]对船舶纵倾优化的原理和方法进行了总结，并以4250TEU型船舶为例，根据水池实验和实船试航数据，认为各类船型在不同装载状况和航速下，对应有不同的最优纵倾，并对纵情优化的实施和推广提出了许多意见。谢玲玲[4]等应用商业软件FLUENT对复杂船型的阻力性能进行了数值模拟计算，并将计算得出摩擦阻力系数与ITTC公式结果相比较，验证了数值计算的正确性。吴明[5]等基于CFD的方法，用三种动网格相结合的方法，在数值计算中还考虑了螺旋桨的影响，计算了船模在浅水下航行的下沉量和纵倾值，并与船模水池试验结果吻合良好，认为用CFD的方法计算船模的下沉量和纵倾值是可行的。

本文中船舶纵倾优化就是以LPG型船舶为例，在已知船模试验数据的情况下，通过理论结合实际的方法，首先分别应用CFX和FLUENT两种软件进行设计吃水状态下的船模CFD阻力性能仿真计算尝试，比较两种软件的计算结果，并通过水池船模试验对其进行抽样验证，从中选取比较合理的运算方式。再通过大量的模拟数据计算出不同吃水和航速下的船舶阻力值，分析计算结果，最终推算出不同吃水和航速下的LPG船舶的最优纵倾。引进系统优化思想，以最小阻力为目标，给出LPG船舶航行最佳纵倾浮态，为LPG船舶及其他肥大型船舶实际营运中最佳纵倾操作提供建议，达到节能减排的目的。

1 船模阻力实验

1.1 船模制作

本文给定的某LPG船的主尺度见表1。

表1 实船主尺度Table 1 Main dimensions of LPG

确定缩尺比λ=33.239后，即进行船模下料图的绘制与卡板的制作，用于船模的制作与检验。船模制作包括下料、成型、打磨、油漆、绘制水线等过程。对于本次试验船模，还增加了艏艉吃水线附近的刻度绘制，以便调整纵倾状态时准确读数。在船模制作过程中以及制作完毕后，一直使用卡板进行检验，尽量将误差减到最小，船模见图1。

图1 船模图片Fig.1 The ship model

1.2 模型阻力试验状态

船模试验选取了LPG船的三个典型工况，试验状态一对应的是LPG实船设计吃水状态，实船吃水为9.8 m；试验状态二对应的是实船某一工作工况的吃水状态，实船吃水为8.931 m；试验状态三对应的是实船压载吃水状态，实船吃水为6.112 m。模型阻力试验状态见表2。

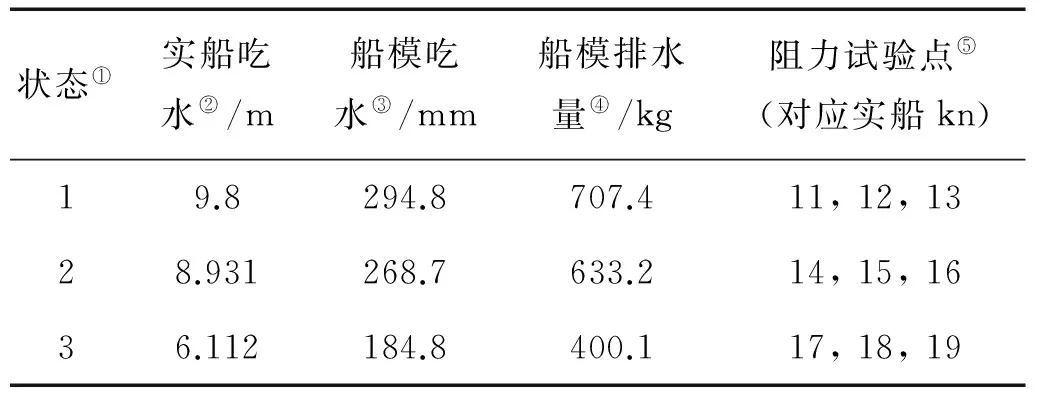
表2 模型试验状态Table 2 Testing program of the model

Note：①Condition；②Real ship draft；③Ship model draft；④Ship model displacement；⑤Resistance test point

船模试验情况见图2。

图2 试验中的船模Fig.2 Test processing

1.3 模型阻力试验结果

船模试验结果见表3。

表3 船模实验结果Table 3 Testing result of the model

Note：①Real ship speed；②Ship model speed；③Ship model resistance；④Condition 1；⑤Condition 2；⑥Condition 3

2 计算模型

2.1 控制方程

本文运用CFX和FLUENT两种软件进行仿真计算尝试，软件中采用了惯性坐标系下的不可压缩Navier-Stokes方程，控制方程具体形式为：

连续性方程：

(1)

动量方程：

(2)

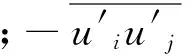
2.2 模型的建立

该船二维型线图由CAD完成，三维模型使用三维建模软件PROE完成。阻力数值仿真计算采用的船体模型大小与试验船模参数一致，数值计算流场的宽度和水深分别参照了模型实验所在水池的尺寸。将LPG船型数据转换成三维坐标，在PROE输入坐标点后，用样条曲线光顺连接，得到LPG船体三维型线，构建基本框架，见图3。

图3 三维型线Fig.3 Three-dimensional lines

通过三维型线生成多块曲面，并将曲面合并成面组，得到整个LPG船体的曲面模型。将船体各个曲面合成封闭曲面并实体化，最终得到LPG船舶的数字计算模型。图4即是船体实体模型。

图4 船体实体模型Fig.4 Hull entities model

2.3 计算域及网格的划分

计算时采用的是对称模型，以船模中纵剖面为对称面。考虑到阻力计算对应的傅氏数较广，数值模拟区段约4倍船长，空气和水的入口在船艏上游L处，出口在尾部下游2L处，侧面在距离船表面L处，底部在里船体表面L/2处。计算域分为空气域和水域，两者的分界面即为船体模型水线面，水线面以上为空气域，以下为水域。计算域总体大小参照实验水池。对应于LPG各个不同的工作状态，变化空气域、水域各自的大小。

网格划分通过ICEM来完成，全部采用六面体网格。全局采用H型网格，船体附近采用C型网格。船体表面曲线变化较大，需要将船体分成多个block来进行网格划分，船体中间部分线型比较平缓，只需分成几个大的block就可以形成质量高的六面体网格，而首尾曲线变化较大，需要对艏部和艉部网格进行局部加密，这样不会出现扭曲率太大的网格，给计算造成麻烦。网格线尽量正交，曲线尽量光滑。网格见图5～6。

图5 计算域网格Fig.5 Computational domain grid

图6 船体表面网格Fig.6 Hull surface grid

2.4 仿真计算设置及尝试

2.4.1 Fluent计算设置 使用Fluent软件来进行计算，采用的是全计算域结构型网格。在计算过程中分别尝试了Fluent中的各个湍流模型来计算船模阻力，包括标准的k-ε模型、RNG k-ε模型、Realizable k-ε模型、标准k-ω模型、SST k-ω模型。

空气入口为速度入口，湍流强度为0.1%，湍动黏度比为1，水的入口也为速度入口，湍流强度为1%，湍动黏度比为1，给定速度出口与入口相同的边界条件，计算区域的上面和空气入口条件相同，底面与侧面设定为壁面边界条件，船体表面也给为壁面边界条件，中间给定对称面条件。进口速度为1.428 m/s，水温与实验条件相同。

自由表面的求解选用了欧拉隐式VOF方法，它可用于定常和非定常计算。由于网格质量的问题，采用非定常计算来求解，所采用的时间步长作为伪时间步，以逐步逼近稳态解。为了能够较好的收敛，刚开始时间步长取为0.001 s，当快要收敛的时候，时间步长取为0.005 s，每个时间步长内迭代20 次，对于不同的网格，不同的湍流模型，经过40 s以上的计算以后都可以得到稳定的阻力系数收敛曲线。压力的插值方法采用了PRESTO(PressureStaggering Option)，其它的项都用二阶迎风格式进行离散，包括体积分数，选择求解自由面相对准确的几何重构等方法。速度压力的耦合方法为SIMPLE(Semi-Implicit Method for Pressure-Linked Equations) 方法。为了加快算法的收敛性，Fluent软件采用了多重网格技术来加速收敛，即对网格进行粗细划分，先消除高频脉动的误差，再消除低频脉动的误差，直到收敛。

对比所有的湍流模型的计算结果，RNG k-ε模型在计算一些复杂的剪切流、有大应变率、漩涡、分离等流动如肥大型船舶的流场时，配合标准的壁面函数计算的结果与试验结果的误差在5%以内，并且计算收敛性好，计算速度快。

2.4.2 CFX计算设置 CFX设置除了域的上表面采用开放式的(Opening)边界条件外，其余边界条件基本与用fluent计算时的边界条件相同。这样方便将两种方法的结果进行对比。模拟类型采用非稳态的模拟，总持续时间设定为30 s，时间步长设定为0.002 s。流动模型设定中选择Homogeneous Model选项，则域内采用了均相流模型，气体和水具有相同的速度，设定自由表面模型为Standard，则水相和空气相之间有明显的分界。湍流模型设定保持默认的k-ε设定，壁面函数为Scalable。差分格式采用高阶求解模式，瞬态格式采用二阶向后欧拉模式。计算结果经过后处理能够很直观地观察船体表面动压力分布及船行波等数据。计算结果显示CFX计算有一定的精度，但是它计算的收敛性不太好，计算耗时，并且它对摩擦阻力的计算不太准确，部分航速状态下的计算误差达到了5%以上。

图7 CFX计算所得波系图Fig.7 Wave system calculated by CFX

3 仿真计算结果对比

根据仿真计算结果，计算方法采用FLUENT中的RNG k-ε湍流模型配合标准的壁面函数的计算方法对全结构性计算网格的流场进行计算。LPG型船舶在设计吃水下的计算结果如下表所示(纵倾值为正，表示尾倾，纵倾值为负，表示船舶首倾)：

表4 船模阻力计算结果Table 4 FLUENT calculated resistance

仿真计算阻力值与模型试验阻力值的相对误差如下表所示：

表5 船模阻力数据比较Table 5 Results comparison

如上表结果，采用Fluent中的RNG k-ε湍流模型配合标准的壁面函数的计算方法所得船模阻力值与船模实验测得的阻力值最大误差均在5%左右，证实用FLUENT中的RNG k-ε湍流模型配合标准的壁面函数的计算方法来计算LPG船舶的阻力是比较可靠的，计算结果可以达到纵倾优化数据分析的要求。

4 计算结果与分析

根据流体动力学分析，船舶水阻力受排水量、水深、船速和纵倾角有关。船舶在装载量一定的情况下(即排水量一定)，如果改变其纵倾角，则船舶水下体积几何形状将会改变，船体水线形状和水线长度、浮心位置、船首来流、船尾去流将相应改变，这些变化必然导致船舶航行期间阻力的改变(兴波阻力、摩擦阻力和粘压阻力)；同时由于船舶航行姿态的改变，不同的纵倾角也将引起船舶尾部流场的变化，进而影响到船舶螺旋桨的推进效率。排除水深因素影响，不同线型的船舶在其不同吃水、不同的航速的工况下应有一个明确的最佳浮态与其对应，在此浮态下该船舶阻力最小。

本文以LPG型船舶为例子，使用FLUENT中的RNG k-ε湍流模型配合标准的壁面函数的计算方法对LPG船舶在两个吃水状态的不同倾角状态下的阻力值进行了仿真计算，计算结果如下：

当LPG型船舶实船吃水达到设计吃水9.8 m时，船模首倾且船舶航速较低时，相比于平浮状态下船模的阻力减小，在其余状态下则出现增阻现象。特别是在尾倾状态时，尾倾角度越大，阻力值增加得越多。所以LPG型船舶船吃水为9.8 m航速为12 kn时，船舶首倾且首位吃水差为1.77 m时有2.41%的节能效果；船舶航速为14、16、18 kn时平浮状态时能耗最低。

表6 吃水为9.8 m时的CFD计算阻力数据Table 6 CFD calculated resistance when draft is 9.8 m

表7 吃水为8.931 m时的CFD计算阻力数据Table 7 CFD calculated resistance when draft is 8.931 m

当LPG型船舶实船吃水为8.931 m时，计算结果显示船模在首倾状态下都有一定程度的减阻效果，而且首倾角度越大，减阻效果越明显；当船舶处于尾倾状态时，在实船航速为12和18 kn时船模减阻，其余状态下船模阻力增加。所以LPG型船舶船吃水为8.931 m时，12 kn航速对应阻力最小的状态为尾倾且首尾吃水差为2.91 m；14和16 kn航速船舶在首倾且首位吃水差为1.86 m时减阻效果最明显；船舶航速在18 kn时，船舶尾倾且首位吃水差为0.57 m时最节能。

当LPG型船舶实船吃水达到压载吃水6.112 m时，船模首倾且船舶航速较低时，有减阻效果，在其余状态下则出现增阻现象。在船舶处于尾倾状态航速大于12 kn是有一定的减阻效果。所以LPG船吃水为6.112 m航速为12 kn时，船舶首倾且首位吃水差为2.1 m时有1.4%的节能效果；船舶航速为14、16、18 kn尾倾角度越大减阻效果越明显。

5 结论

本文通过对调节纵倾来改善船舶阻力的原理进行分析，对以某LPG船为例进行了船模阻力实验，分别用CFX和FLUENT软件对LPG船进行仿真计算尝试，经过与船模实验结果对比，最后选择FLUENT进行了数值模拟，根据计算结果，可以得出以下结论：

(1)用FLUENT中的RNG k-ε湍流模型配合标准的壁面函数的计算方法来进行类似LPG的肥大型船舶的数值计算与船模实验结果误差较小，结果可靠度高。

(2)排除水深影响因素外，LPG型船舶在不改变船舶航速、载重量的前提下可以通过纵倾调节来减少船舶阻力，达到节能减排的作用。

表8 吃水为6.112 m时的CFD计算阻力数据Table 8 CFD calculated resistance when draft is 6.112 m

(3)与传统的通过船模试验的方法对船舶进行纵倾优化相比，采用仿真模拟计算的方法，在满足计算精度的情况下，计算速度快，计算结果直观，易于比较。

(4)试验以及仿真计算中所得减阻数据和结论可以为LPG船舶以及类似的肥大型船舶实际运营提供指导。

当前船舶和航运行业形势十分低迷，控制成本是每家航运公司增强竞争力十分关键的一项举措。船舶纵倾优化是一种不需要改变船体构造、不附加安装设备的节能方式，不仅不降低船舶载货量、不降低航速、易于实施并且效果显著，有一定的推广前景。

参考文献：

[1] 王维宇, 林洪波, 何惠明. 纵倾船舶的稳性计算方法[J]. 上海船研所学报, 1985(1): 67-78.

WANG Weining, LIN Hongbo, HE Huiming. A calculation method of stability for a trimmed vessel[J]. Journal of Shanghai Scientific Research Institute of Shipping, 1985(1) : 67-78.

[2] 邵世明, 王云才, 钱章义, 等. 高速排水型艇的初始纵倾对阻力影响的试验研究[J]. 上海交通大学学报, 1996(10): 136-140.

SHAO Shiming, WANG Yuncai, QIAN Zhangyi, et al. The expermental investigation on influence of original trim upon resistance for high speed displacement hull forms[J]. Journal of Shanghai Jiaotong University, 1996(10) : 136-140.

[3] 邱斌彬. 船舶纵倾优化[J]. 中国船检， 2014(2): 70-74.

QIU Binbin. Ships trim optimization[J]. China Ship Survey， 2014(2): 70-74.

[4] 谢玲玲, 陈顺怀, 吴静萍. 应用FLUENT软件优化船舶阻力性能[J]. 华中科技大学学报(自然科学版), 2009(6): 101-103, 124.

XIE Lingling, CHEN Shunhuai, WU Jingping. Optimization of the resistance prooerty of ship by Fluent software[J]. J Huazhong Univ of Sci and Tech(Natural Science Edition), 2009(6): 101-103, 124.

[5] 吴明, 王骁, 应荣镕, 等. 船舶浅水航行下沉量和纵倾的数值计算[J]. 船舶, 2013(03): 7-11.

WU Ming, WANG Xiao, YING Rongrong, et al. Numerical calculation of ship sinkage and trim in shallow water[J]. Ship and Boat, 2013(03): 7-11.

[6] 倪崇本, 朱仁传, 缪国平, 等. 一种基于CFD的船舶总阻力预报方法[J]. 水动力学研究与进展A辑, 2010(5): 279-286.

NI Chongben, ZHU Renchuan, MIAO Guoping, et al. A method for ship resistance prediction based on CFD computation[J]. Chinese Journal of Hydrodynamics A, 2010(5) : 279-286.

[7] Kim K J. Ship Flow Calculation and Resistance Minimization[D]. Chalmers University of Technology, Sweden: Gothenburg, 1989.

[8] Kim Y H, LucasT. Nonlinear effects on high block ship at low and moderate speed[C]. Proc 19th Symposium Naval Hydrodynamics. Korea: Seoul, 1992: 43-52.

[9] Ni S Y. Heigher Order Panelmethod for Potemtial Flows with Linear of Non-linear Free Surface Boundary Conditions[D]. Gothenburg Sweden. Chalmers Univ. of Technology, 1987.

[10] Raven H C. A Practical Nonlinear Method for Calculating Ship Wave-making and Wave Resistance[C]. Seoul: Korea, Preprints 19th Symposium on Naval Hydrodynamics. 1992: 60-75.

[11] Xia F. Numerical Calculation of Ship Flows Emphasis on the Free Surface Potential Flow[D]. Gothenburg: Sweden.Chalmers Univ. of Technology, 1986.