会想象才能解好题

张晓梅 潘备战

在人教版数学教材五年级下册第三单元长方体和正方体这一单元中，有一道特别有趣的数学题：用棱长1cm的小正方体拼成如下的大正方体后，把它们的表面分别涂上颜色。

（1）①、②、③中，三面、两面、一面涂色以及没有涂色的小正方体各有多少块？

（2）按这样的规律摆下去，第④、⑤个大正方体的结果会是怎样的呢？

（3）你还能继续写出第⑥、⑦、⑧个大正方体中4类小正方体的块数吗？

此题的综合性非常强，考查学生的观察和想象能力，第①、②、③个大正方体中，小正方体的个数学生可以通过摆拼教具，然后观察、数数得出来。按这样的规律摆下去，第④、⑤个大正方体的结果会是怎样的呢？这时摆拼教具根本行不通了，教师可以通过画图帮助学生直观形象地理解。而利用前面5个大正方体得出的规律续写第⑥、⑦、⑧个大正方体的4类小正方体的块数是本题的难点。要解决这个难点，学生的思路是否开阔、活跃尤为重要。

为了解决问题，教师可以引导学生将问题用列表的方式表示出来，便于比较、观察。图①的解答很容易，学生只需要用小正方体摆一摆、数一数，就可以轻松得到如下结果。

对图②，学生可以先用小正方体进行摆拼，然后仔细观察，边观察边说，并用手指出三面涂色的小正方体的块数。（共8块）

师：两面涂色的小正方体的块数，同学们有什么好方法可以知道？

学生独立思考后交流汇报。

师：通过刚才的分析，同学们都能用不同的方法数出两面涂色的小正方体的块数，说明同学们都动脑思考了问题。那么一面涂色的小正方体的块数怎么数？

生1：这个很好办，正面除了三面涂色的、两面涂色的小正方体，一面涂色的小正方体只有最中间的1块，正方体一共6个面，所以一共有1×6=6（块）。

师：没有涂色的小正方体的块数，你们又是怎样得到的呢？

学生思考后交流汇报。

师：同学们观察仔细，分析得有理有据，不但用自己的方法得到了答案，还通过比较，有更简便的算法，下面的表格请自己补充好。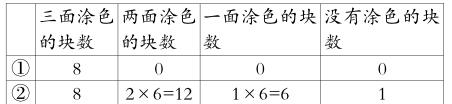

師：图②已经解决，请同学们按照刚才思考交流的方法自主合作解决图③。

一段时间的合作交流后，我让学生汇报结果。对于三面涂色的小正方体的块数，学生都说不用想了，就是8块。对于两面涂色的小正方体的块数，师生通过讨论，一致同意可以先看大正方体的正面，正面有4块，正方体共6个面，所以一共有4×6=24（块）。而一面涂色的小正方体的块数只需看正面图形的正中间，所以一共有2×2×6=24（块）。没有涂色的小正方体的块数，学生通过反复推敲，认为应该按体积公式来算最好，那就是2×2×2=8（块）。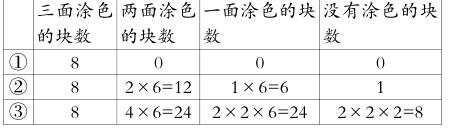

师：那第④、⑤个大正方体，按照刚才得出的规律，你们能写出来吗？很多同学说，第①、②、③个大正方体既有图形看，也能摆拼出来，容易得出结果；第④、⑤个大正方体就只能凭想象了，你能否在黑板上画出来，以便我们更好地理解。确实，几何直观对于教师和学生而言都是一种有效的学习方式，画图就是借助直观，把复杂的数学问题变得简单易懂，有利于探索解决问题的思路。请大家跟我一起画图吧。

教师一边画一边讲解画图的方法，使学生掌握画图的基本技能，帮助建立解题模型。

师：第④、⑤个大正方体已经画好了，请同学们继续合作交流，把表格补充完整。

学生有了前面的经验，对题目的理解也更透彻，填表如下：

师：第①、②、③、④、⑤个大正方体我们都已经按要求填好了表格，那么第⑥、⑦、⑧个大正方体请大家独立思考完成，一定要想清楚你是怎样填的，填的根据是什么，有什么规律。

学生开始动手研究，然后填表，分组汇报。

生2：三面涂色的小正方体的块数对于任何一个由小正方体拼成的大正方体来说都是一样的，是它的8个顶点所在的小正方体，就是8块。

生3：两面涂色的小正方体的块数，第①个大正方体中没有，从第②个大正方体开始，每一面都是增加的，而且是连续偶数2、4、6、8、10、12、14……只要用一面的块数×6，就是整个大正方体两面涂色的小正方体的块数，所以第⑥、⑦、⑧个大正方体中两面涂色的小正方体的块数分别是：10×6=60、12×6=72、14×6=84。

生4：一面涂色的小正方体的块数就更好填了，只要看大正方体正面正中间的图形，它其实也是一个小正方形，用边长×边长就得到一面的块数，再×6就行了。所以正确答案分别是：5×5×6=150、6×6×6=216、7×7×6=294。

生5：没有涂色的小正方体的块数，就是大正方体正中间的小正方体，它的块数是边长×边长×边长，可按体积公式计算。所以我写出来的分别是：5×5×5=125、6×6×6=216、7×7×7=343。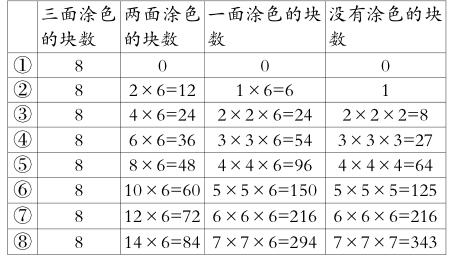

数学课堂教学中，教师应注意激发学生的学习兴趣，调动学生的积极性，引发学生的数学思考，发展学生的创造性思维。这些基本活动经验是教师没有办法教给学生的，必须由学生自己通过大量的数学活动获得。上述教学中，教师让学生通过摆拼、观察、画图、想象、合作、交流，自己寻找解题规律。在这一过程中，学生经历探究、思考、抽象、推理、反思等活动，在获得数学知识的同时培养了解题能力。

（作者单位：永州市冷水滩区朱家山小学永州市冷水滩区杨家桥小学）